冰的氢键振动研究*
2021-08-05秦晓玲朱栩量曹靖雯王浩诚张鹏
秦晓玲 朱栩量 曹靖雯 王浩诚 张鹏
(山东大学威海校区空间科学与物理学院, 威海 264200)
虽然水分子结构简单, 但是关于水冰的基本理论仍有很多问题没有科学答案. 对于冰的原子分子振动,人们对其分子内的伸缩和弯曲振动以及分子的空间转动已经研究得很清楚. 然而30年前, 高亮度的非弹中子散射实验发现, 很多冰相的远红外分子平移区中存在两个明显的特征振动峰, 对其来源一直没有定论. 本文基于第一性原理密度泛函理论的CASTEP代码, 系统研究了不同冰相的振动谱和振动模式. 在对最简单的氢有序冰Ic模型的研究中, 首次发现了两类本征的氢键振动模式. 以此为线索, 继续模拟其他的冰相, 发现无论是氢有序还是氢无序结构都存在这个规律. 利用冰晶格局域正四面体理想模型, 理论上证明了两类振动模式可分为围绕一个水分子的氢键的四键振动和双键振动. 高压下, 因为结构变形, 存在介于二者之间的耦合振动. 此外, 还有能量更低的一些光学支振动模式, 比如团簇的振动、面间振动. 冰VII/VIII, XV/VI等结构,是由两个子晶格嵌套而成的, 两个子晶格之间还有非氢键的相对振动. 综上, 这些分子平移振动可解释所有冰相的远红外振动谱, 为冰的分子振动理论补足了最后一块拼图. 由于液态水不存在这两类氢键振动, 因此其远红外吸收带在两个氢键位置恰好是个波谷. 结合太赫兹激光技术的发展, 此理论有望在工业除冰、食品解冻、可燃冰开采和生物分子冷冻塑型等领域产生系列原创成果.
1 引 言
1.1 液态水中的氢键
水作为地球上最丰富的物质之一, 覆盖了约71%的地球面积. 水是生命有机体最重要的组成部分, 也是所有生命赖以生存的重要资源. 尽管水分子结构简单且均匀, 但它具有许多不同于其他液体的异常性质[1], 吸引了大量科学家的关注和广泛研究. Pauling[2]提出氢键的概念后, 液态水的微观结构才开始得到深入研究. 20世纪80年代以前, 基于常态冰的四面体氢键网络结构的启发, 提出了液态水的连续模型[3]和混合模型[4,5]. 液态水的经典混合模型[6]认为, 水分子之间的氢键存在着类似冰的四面体网络结构, 但水分子的位置不是固定的,且这种四面体结构处于不断地解体和重构的动态过程中. 直到2004年, Nilsson课题组[7]提出“绳圈”模型引起了强烈的争议, 该模型认为每个水分子平均形成两个氢键, 导致水分子呈链与环状结构. 但很快Saykally课题组[8]提供了新的实验证据, 证明经典模型仍是最合理的模型, 且每个水分子平均形成3.3个氢键. 基于拉曼光谱研究, Sun[9]发现这两种模型以一定比例存在于液态水和过冷水中. 在常温水中大致相同, 随着温度降低至过冷水时, 绳圈结构会转变为四面体结构. 关于水中的氢键在两种模型之间如何转换的问题, 一直处于争论中[10-16].
1.2 众多冰相的发现历程
冰作为水的一种凝聚态形式, 是地球上最常见的分子晶体. 在一定的压强和温度下, 冰已被发现超过20种不同的晶相和非晶结构[17-37]. 自然界最常见的三维冰相为六角冰(Ih). 然而, 对于冰在二维情况下能否稳定存在学术界一直有争论[38,39].Koga等[40]利用分子动力学模拟首次预测了这种“互锁型”双层二维冰, 但一直缺乏确切的结构实验证据. 2020年, 北京大学量子材料中心江颖、徐莉梅与美国内布拉斯加大学林肯分校曾晓成以及北京大学王恩哥等[41]合作, 利用高分辨qPlus型原子力显微镜技术(AFM), 首次在实验上证实了冰在二维极限下可以稳定存在, 并将其命名为二维冰I相.
据目前的研究结果, 人们已经发现了至少18种不同的冰晶结构, 但大部分是在一定的压强和温度下通过实验制备获得. 其中, 只有六方相冰Ih和立方相冰Ic可以在自然界中自发形成和存在. 冰Ih是一个相对开放的低密度晶体, 密度约为0.926 g/cm3, 是具有六重轴高对称性的六角冰, 其原胞可以看作是由两个反向六元环构成[42].Konig[43]是第一个发现并推导出冰Ic相结构的人.冰Ic与冰Ih有几乎相同的密度和晶格常数(沿着六角形边方向)[44]. 立方冰Ic晶体具有亚稳态的面心立方结构, 密度约为0.933 g/cm3, 在温度约为235 K时由纯水滴均匀结晶形成[45,46]. 又或者在77 K 时由高密度冰通过减压的方法相变而来[47].Whalley[48]在太阳光折射光晕中首次发现了自然界中存在立方相冰Ic. 非晶冰[49]以及冰II, III和V可以在高压下产生冰Ic. 然而, 大的高纯度冰Ic是很难通过实验合成的[50,51]. 在过去的几十年中, 大量制备高纯度立方相冰Ic的方法被开发[52-54], 能够制备纯度70%以上的氢无序堆积冰[55]. 直到2020年2月, del Rosso等[56]和Komatsu等[57]分别提出了两种制备无堆砌缺陷、纯度100%立方相冰Ic的方法. Lekner[58]计算了大约90种氢构型,以研究含有8个水分子的冰Ic晶胞中氢排列的能量变化.
在不同的温度和压强条件下, 水分子之间的氢键呈现出不同的网络结构和强度, 因此对应着极其丰富和复杂的相图[59,60]. 此外, 冰相还有氢有序和无序排列的成对的异构体. 从熵的角度看, 当温度降低时, 熵减少, 氢在晶格中的排列方式应该趋于一致, 即有序化. 因此, 存在很多氧原子晶格相同但氢原子排列不同的冰相结构, 被称为冰对. 已知的冰对有Ih/XI, III/IX, V/XIII, VI/XV, VII/VIII,XII/XIV[61]. 但是没有发现冰II对应的氢无序冰相.
1900年Tammann[18]通过加压发现了氢有序相冰II. 1964年, Kamb[62]首先通过单晶X射线衍射对冰II进行了结构分析, 得到了冰II中的氢有序的证据. 冰II相的结构是基于空间群的菱形单胞, 其晶格常数为a= 7.78 Å和α= 113.1°, 密度为1.17 g/cm3. Finch[63]和Kamb等[64]使用中子衍射实验来验证冰II中的排序方案.
在0.2 GPa的压力下, 常态六角冰Ih能够转化成冰II. 当压强超过0.5 GPa时, 冰II相可以转变为冰V或冰VI, 它们都是高密度的多晶型态.2003年, Fortes等[65]使用从头算方法模拟对冰II相加热, 发现温度达到240 K以上时冰II转变为冰III, V或冰VI结构. 目前获取冰II的标准方法是在约200 K下将六角冰Ih等温压缩, 也可以通过对冰V减压或冷却来获得[66,67]. 在20世纪60年代, Bertie等[68,69]首次测量了冰II相(还有III,V, IX相)的红外光谱. 随后Bertie和Francis[70,71]以及Li等[72]报道了其拉曼散射和INS实验谱.
1912年, Bridgman[21]通过加压发现了高压相冰VI. 在常压和液氮温度下, Kamb[73]通过X射线衍射得到了冰VI的晶体结构. 冰VI的原胞中含有10个水分子, 其空间群为P42/nmc, 为氢无序相. 冰VI由两个相互交叉但又彼此独立的氢键网格组成, 因此被称为“自笼型包合物”. Kuhs等[25,74]通过中子粉末衍射实验进一步证实了冰VI结构.
2009年, Salzmann等[33]通过低温下掺杂HCl,发现了冰VI的氢有序相, 称为冰XV. 这种氢有序结构是反铁磁性结构(), 可以稳定存在于130 K以下和0.8到1.5 GPa之间. 2013年, Whale等[75]测量了冰XV的拉曼光谱, 并使用第一性原理密度泛函理论进行了模拟. 随后, Salzmann等[76]与Nanda和Beran[77]又提出了VI的另一种氢有序结构, 即具有空间群Cc的铁磁结构. 2018年,Gasser等[78]证明了另一个对应的XV相的存在,他们称之为冰β-XV相, 对比测量了两种冰XV样品的拉曼谱.
Klotz等[79]发现可以在3 GPa以上通过冷却液态水至室温, 或在95 K以下通过对冰VI减压产生高压相冰VII. Bridgeman[22]首次提出冰VII可以稳定存在于常温以及22 kbar (1 bar = 105Pa)的压强下. 冰VII的结构由两个相互套构的立方Ic晶格组成, 子晶格之间没有相互连接的氢键[25].
1966年, Whalley等[24]首次在实验中发现在0 ℃以下, 会出现一种由冰VII转化而来的具有极低介电常数的冰相, 即冰VIII相. 作为冰VII的有序相, 冰VIII也有两个套构但非键合的子晶格.Vaks和Zinenko[80]也发现在275 K左右, 冰VII可以由无序相转变为有序相冰 VIII, 且两个亚晶格中的氢排序是反平行的. 红外吸收(IR)[81]、拉曼散射(Raman)[82,83]、中子衍射[25]等实验都为冰VII到冰VIII的转换过程提供了可靠证据. 两个冰Ic相的结构反向嵌套形成冰VIII, 其每个原胞包含4个水分子, 空间群为I41/amd. 人们已经对冰VIII振动谱进行了各类研究. 然而, 冰VIII振动谱峰的指认仍存在许多不确定性.
红外光谱实验证实了压强高于60 GPa时, 冰VIII和VII会转换成冰X[84,85]. 通过X射线衍射实验, 研究人员发现在温度125 K以上时, 冰VIII转化成低密度无定形冰(LDA)[86].
冰III具有氢无序结构, 存在于—24 — —44 ℃,2.4—3.4 kbar. Whalley等[26]发现, 在—65— —108 ℃时, 冰III可以转化为一个新的氢有序相, 即冰IX.通过IR[70], Raman[87]和中子散射[88]等实验来表征冰III和IX. Garg[89]和Tse等[90]通过拉曼散射实验发现, 在150 K时对冰Ih加压可以将其转化为冰IX.
1972年, Holzapfel[91]首次预测了高压相冰X,其结构为: 氢原子位于两个相邻的氧原子中间位置. Polian和Grimsditch[92]报告了固态冰的高达30 GPa布里渊散射实验的结果. 后来, 他们再次将这类实验增加到了67 GPa, 也发现了新的高压相冰X的存在. Hirsch和Holzapfel[28]预测: 在一定压力和温度的条件下, 冰VIII相可以转变成冰X相. 冰X相晶体密度约为2.785 g/cm3, 是对称的立方结构. Flores-Livas等[93]从理论上证实了:在温度为60 K, 压强环境为150 GPa的条件下,冰X相晶体中掺杂氮原子会变成超导体. 该发现一定程度上证实了冰X相晶体不再是分子结构,冰X相中氢原子和氧原子被完全电离, 一定条件下具有导电特性. 现阶段已有大量对冰X的物理和化学性质的研究[94-98], 然而在如此高的压力下,无法开展非弹性中子散射(INS)实验.
根据莱纳斯·鲍林所描述的余熵原理, 常温下冰Ih中无序质子的排列不可能是低温下冰的平衡结构[99]. 通过引入K-OH掺杂的缺陷, Kawada[100],Tajima等[27]发现冰Ih相在72 K处发生一级相变, 这个新的有序冰相被命名为冰XI. 中子衍射和确定了冰XI为正方晶系结构, 空间群为Cmc21;所有平行于c轴的氢键取向一致, 具有铁电特性[101-103].
冰XIII是与冰V相对应的氢有序相, 空间群为P21/a. 2006年, Salzmann等[31,104]发现掺杂一定盐酸的冰V降温后可以形成冰XIII. 随后他们报告了冰XIII的拉曼光谱[105]. 2010年Zhang等[106]成功地通过计算再现了冰XIII的结构并给出了冰XIII的声子态密度(PDOS). Tran等[107]最近给出了由重水形成的冰V和冰XIII的红外吸收谱.
1998年, Lobban等[29]在温度260 K、压强0.55 GPa下, 首次制备出新的氢无序的冰XII相.2006年, Salzmann等[31]和Tribello等[32]在一定压强下对掺杂HCI的冰XII相进行冷却, 发现一种新的氢有序冰, 属于P212121空间群, 被命名为冰XIV相. 后来, 研究人员做了大量关于冰XII/XIV相的拉曼和中子散射光谱实验[108-111]. 尽管很多实验都给出了冰XII/XIV的振动谱, 但是对冰XIV特征峰进行标定的理论研究到目前为止仍然是欠缺的.
通常将低于六角冰Ih或XI的密度值(约为0.93 g/cm3)的冰晶体定义为低密度冰相. 目前, 只有两个低密度冰相冰XVI[34]和XVII[35]在实验室中被合成. 它们的密度分别为 0.81 和0.85 g/cm3,人们认为它们在负压下是稳定的[112-117]. 2014年,Falenty等[34]通过真空泵抽离氖气填充的S-II型笼形水合物, 在实验室中制备出了笼形冰结构, 并命名为冰XVI. 然而, 有关其振动谱的资料在文献中缺乏. del Rosso等[35]通过去除C0相中所有的氢分子, 在低于120 K的室温条件下获得了名为XVII的无客体冰结构, 空间群为P6122的六角晶体. 温度为 100 K 时冰XVII的密度为0.85 g/cm3,比相同温度和压强条件下合成的六角冰 Ih 的密度低 11%[118]. 尽管冰XVII相密度远远低于冰 Ih相, 但它们的声子态密度却具有非常相似的特征.冰XVII是由48个水分子构成的氢无序结构的分子超胞, 笼型水分子结构与内部甲烷气体分子之间无化学键, 仅存在分子间作用力.
1.3 超离子态冰相-冰XVIII
早在1988年, 物理学家Demontis等[19]就曾提出一个超离子冰结构的预测. 他模拟了水在极端的压力和高温环境下的情况, 在模拟中, 氧离子被锁在一个固态的立方晶格中, 氢离子(质子)则可以自由移动. 四处扩散的质子赋予了这种冰很强的导电性, 并且也增加了冰的熵, 而熵的增加也反过来使得这一冰晶结构比其他的冰更加稳定, 熔点更高. 直到2018年, LLNL(劳伦斯·利佛莫尔国家实验室 ) 的物理学家 Millot 等[36]找到了超离子冰存在的第一个线索. 他们对液态的水进行压缩, 使得液态水在几纳秒内变成了固态冰. 经过测量发现, 导电性在短时间内比之前增强了数百倍, 这意味着水冰已经变成了“超离子”态. 2019年, 他们发表了新的研究结果[37], 利用激光驱动的冲击波和原位X射线衍射, 在几纳秒内观察到氧晶格的成核, 首次揭示了超离子冰的微观结构. 实验结果表明, 压力在249—278 GPa之间, 温度约在2000—3000 K之间, 可以诱导体心立方相转变为新相, 他们将新相命名为冰XVIII. 冰XVIII氧晶格为密堆积的面心立方相, 空间群为Pbcm, 晶格常数a= 3.417Å.
1.4 冰的原子分子振动研究进展
冰的常态结构Ih相, 通过在20世纪60, 70年代的红外和拉曼等实验研究, 已经对其分子平动、分子转动、分子内剪切和伸缩振动有了较清晰的认识[119,120]. 据报道, O-H伸缩带、转动带的中心在3300, 850 cm—1左右, 平移带最大红外吸收在229 cm—1左右, 范围从0—325 cm—1. 关于冰的拉曼谱, Rasetti[121]报告了在53.52和212.1 cm—1间的宽频带. Hibben[122]报道了约以205 cm—1为中心, 至少到300 cm—1的振动带, 并认为是分子间的振动. Cross等[123]将其归因于水分子的平移振动.Narayanaswamy[124]报道了Rasetti的在53.5 cm—1处的波段, 而且在213 cm—1波段附近有一个宽幅波段, 一直延伸到310 cm—1, 这一点已被Valkov和Maslenkova[125]证实. Taylor和Whalley[126]报道了在77 K下H2O和D2O冰的拉曼光谱, 分别在225和217 cm—1处有极大值, 并标定为分子的平移振动. 以冰Ih的计算谱为例, 图1中标记了四个独立的振动带, 分别是平移振动带、转动振动带、弯曲振动带和伸缩振动带.

图1 常态冰Ih相的声子态密度(PDOS)谱. 横轴波数的单位是cm—1, 四个独立的振动带从左到右依次是分子间平移振动带(translation), 分子转动振动(libration)带, 分子内弯曲振动(bending)带, 分子内伸缩振动(stretching)带Fig. 1. Phonon density of states (PDOS) spectrum of ice Ih.The four independent vibration bands from left to right are translation band, libration band, bending band, and stretching band.
冰Ih相的红外吸收谱在220 cm—1位置的特征振动峰也被归因于氢键的振动. 然而, 20世纪90年代新的实验技术—高通量非弹性中子散射实验(测量于英国卢瑟福国家实验室散裂中子源的TOSCA谱仪)却发现冰的远红外区普遍存在两个显著的振动峰, 对这两个振动峰的来源学术界一直没有定论. Marchi等[127]计算了冰晶格振动的光学纵波-横波分裂, 但得到的能量差仅为10 cm—1.Renker[128]认为由于各向异性, 沿着光轴或垂直于光轴会有两个氢键强度. 对于冰Ih相, 在226和303 cm—1[129]处有两个独立的振动峰, 对应于振动谱上230和310 cm—1的波数. 对此, Klug等[130]讨论了冰Ih中的光学支纵波-横波(LO-TO)分裂.而Li和Ross[131,132]提出了一种基于静电相互作用的晶格动力学模型. 他们认为存在两个氢键力常数, 分别为1.1和2.1 eV/Å, 即弱氢键与强氢键的比值为1:1.9. 虽然Li的模型能够解释Ic和Ih的氢键峰劈裂, 但并没有被广泛接受[133-136]. Morrison和Jenkins[133]认为, 氢键振动的分裂是由于与分子内伸缩振动的耦合. Klotz等[134]认为是振动峰分裂是因为声子色散曲线的测量不完整. 我们利用第一性原理密度泛函理论的方法模拟了冰Ih的振动谱, 首次模拟出两个氢键振动峰[135], 观察到了平移带的分离如图1所示. He等[136]也否定了Li的模型, 并将其笼统地解释为沿不同运动方向的声子极化.
从氢有序冰Ic相开始研究, 起初我们认为远红外区的两个振动峰是由横波纵波分裂引起的[137,138]. 之后我们观察位于230和321 cm—1的两种振动模式, 发现这两种不同的氢键振动模式是由于参与氢键振动的数量不同产生的, 我们命名为双键模式和四键模式[139]. 后续的研究发现, 由于晶格中的局域正四面体对称性, 冰相中普遍存在这两类简正振动模式[140-150]. 因此针对冰相平动区存在的两个氢键峰的问题, 我们提出两类氢键模型理论来解释. 本文总结了众多冰相的共同规律, 综合分析了他们的振动谱, 不再局限于单个冰相的振动模式分析和峰值标定.
2 冰相的建模与计算
2.1 建 模
对于氢有序的结构, 如果给定了氧原子的坐标和对称性, 就可以构造出晶体的原胞. 此外, 我们也可以从晶体结构数据库(ICSD)中选择需要的晶体结构. 然而对于氢无序的冰VI, VII和XVII等,理论上没有原胞. 以冰VII为例, 为了模拟冰VII的实际结构, 构建了一个包含64个分子的冰VIII超胞, 并按照B-F (Bernal-Fowler)规则随机重新排列氢原子. 对于笼型结构冰XVII, 先用Genice[151]程序构造出多个超胞[152]. 从概率上说, 这样的结构有很多. 一个合理的自然的结构应该不会出现宏观极化, 因此, 按照宏观极化率最小的原则选择合适的结构作为计算模型. 我们可以采用加压的方法使冰相的结构发生相变产生新的结构, 例如, 尝试计算加压后冰VIII相的变化, 将静水压从60 GPa上升到140 GPa, 取压强间隔为10 GPa, 来观察得到的键长和冰相结构. 随着压强增加, 冰VII相或冰VIII相键长缩短, 密度变大, 氢原子逐渐移动到两个氧原子的正中间. 模拟发现该结构在120 GPa下会转变成空间群为Pn3m的冰X相.
2.2 设置参数
由于氧、氢原子之间电子气密度梯度很大, 选用广义度近似(GGA)下的交换关联函数RPBE[153]作为密度泛函理论近似. 为了测试交换关联(XC)函数, 分别尝试过用RPBE, PBE, PW91, WC,PBESOL进行结构优化. 以密度为1.32 g/cm3的冰XV为例, 测试结果表明, GGA下五种函数下结构优化后的密度分别为1.21, 1.40, 1.41, 1.55,1.56 g/cm3. 由于分子内氢键的长度与体积变化相关, 且振动频率对氢键长度非常敏感, 因此最佳的交换关联函数为RPBE, 尽管它稍微低估了氢键的作用, 使得平移带产生略微的红移, 仍是相对最好的泛函. 对于高压相, 可以在加压计算时根据实验压强的范围取高一点的压强以平衡这个误差.
声子计算对结构优化的要求很高, 能量阈值和自洽场容差可设置到最大, 至少为1 × 10—9eV/atom.因为性质计算中一般用线性响应的方法模拟振动谱, 赝势函数必须选择模守恒赝势. 部分计算参数在表1中给出.
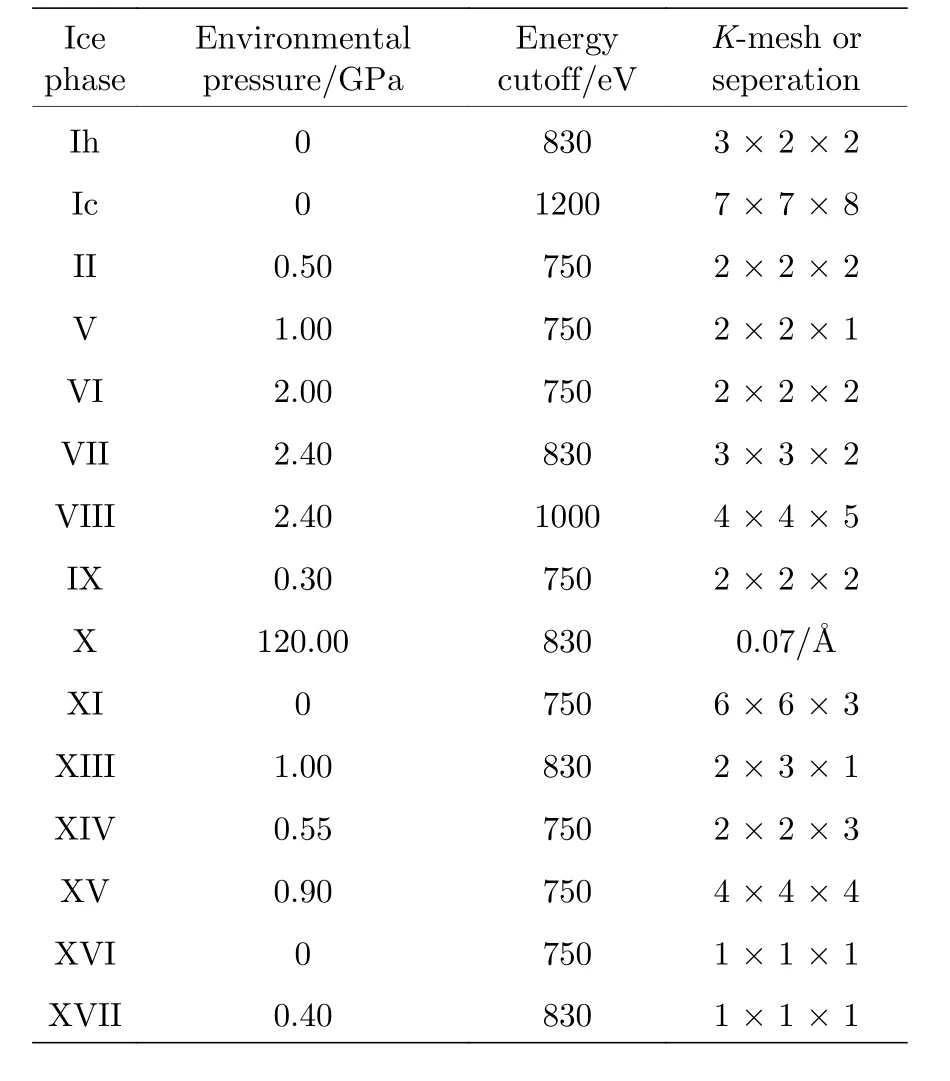
表1 部分冰相的计算参数. 包括静水压强、截断能、K点取样网格或K点间隔Table 1. Calculation parameters of ice phases, including calculation of pressure, cutoff energy, K-mesh or seperation.
实验上, 一般在冰的伸缩振动带有很强的拉曼峰. 在设置压强时, 可以此确定合适的静水压. 比如, 冰II的实验室制备压强为0.2—0.5 GPa, 分别取0.2, 0.3, 0.4, 0.5和1.0 GPa分别进行测试. 实验测得的伸缩带拉曼峰的最强峰在3189 cm—1. 以此为基准, 0.5 GPa下的数据最接近实验值. 因为RPBE泛函略微低估了氢键能量, 因此稍微大一点的压强可以弥补这个误差.
截断能和K点取样的选取因结构而异. 对于大超胞, 因为对应的倒格胞很小, 其色散曲线变化不大, 对K-point的采样可以直接用Gamma点以降低耗时. 比如对冰X的计算, 由于结构十分简单, 每个原胞只含两个水分子, 我们进行了K点取样和截断能收敛性测试. 由于在计算的过程中发生了相变, 选取标准是K点间隔距离而不是K点网格. 图2(a)说明K点取0.07 Å—1的间隔即可, 总能量已收敛. 如图2(b)所示, 将截断能设置在830 eV时, 总能量已收敛. 为了在计算时间和精度上取得平衡, 有时需要进行必要的测试以提高运算效率.因此, 冰X的截断能采用830 eV,K点间隔设置为0.07/Å. 结构优化后, 再进行单点能的性质计算.
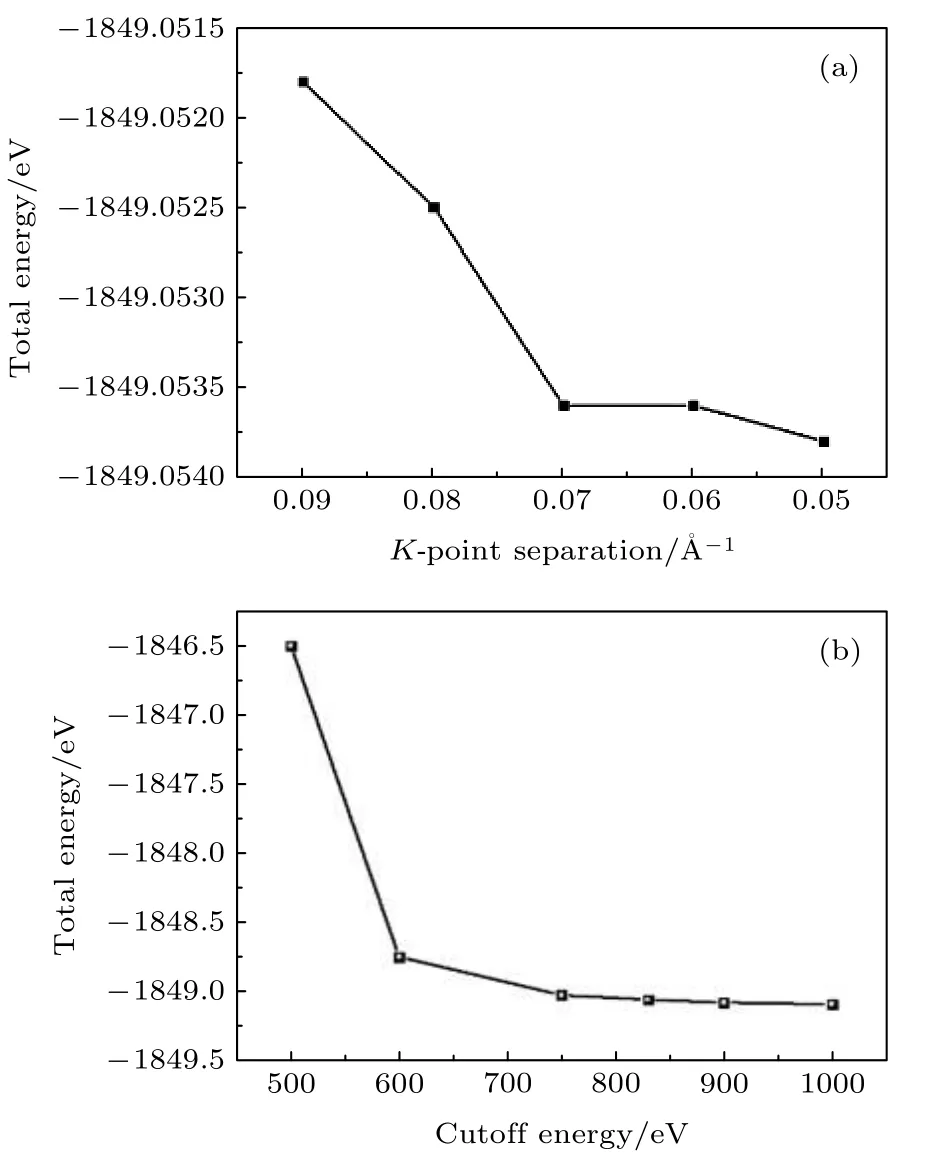
图2 K点和截断能收敛性测试. 总能量与K点间隔的关系如图(a), 与截断能的关系如图(b)[141]Fig. 2. Diagram of the K-point and energy cutoff convergence tests. The total energy against k-point separation is shown in (a) and the cutoff convergence is shown in (b)[141].
计算完成后, 先分析声子态密度(PDOS)以及红外、拉曼谱, 并与实验测量的INS谱、IR和Raman谱相对照. 在计算与实验数据一致的前提下, 进一步研究第一布里渊区中心的简正振动模式. 对于一个含N个水分子的原胞, 其光学支振动模式数为3N× 3 — 3. 因此, 简单的原胞, 如XI, VIII等结构,可以直接分析各个振动模式. 对于超胞, 由于模式数多, 很多模式十分相似, 波数接近, 无法直接解析. 在两类氢键理论的指导下, 设计了一个分析程序, 可以根据振动模式中氧原子的振动方向进行分类. 光学支振动是质心不变的振动模式, 一个超胞含有多个分子, 因此, 会观察到多个分子的集体振动以平衡质心. 平移振动时分子内部保持不变, 可以看作质点. 近似以氧原子为质点, 研究一个振动类型时, 为抓住主要矛盾, 将振动幅度最大的氧原子是沿着H—O—H角平分线还是垂直于角平分线方向进行分类. 在实际的氢无序结构的计算中, 振动模式都是非简并的, 往往呈现某种耦合状态. 因此, 以氧原子的振动方向与角分线的夹角小于还是大于45°为标准进行分类. 自编程序见文献[147].
3 冰的分子振动分析
在精确的结构优化后, 通过计算得到了冰相的简正振动模式和声子态密度(phonon density of states, PDOS)谱. 光子散射收集的是第一布里渊区中心附近的声子信号. 因此, 根据计算所得Gamma点的简正振动可以和红外吸收和拉曼散射光谱相对照, 并依据简正振动模式对测量的峰进行理论标定. 由色散关系曲线积分得到的PDOS谱,反映的是第一布里渊区的晶格振动的全部声子分布, 而非弹中子散射(inelastic neutron scattering,INS)理论上可以与所有声子有能量交换. 因此INS谱与PDOS谱是成正比的, 实验得到的INS谱特征峰可以根据PDOS谱进行标定. 根据四个独立的振动带, 将PDOS谱划分为四个区域去分析. 在此基础上, 我们还发现了冰相中四个振动区振动模式数的规律[150]. 若冰的一个原胞内的分子数为N, 减去三个声学支简正模式, 光学支简正模式总数应为3N× 3 — 3. 伸缩振动带包含2N个振动模式, 对应于对称伸缩和非对称伸缩两种分子内共价键的振动模式. 剪切带包含N种模式. 转动振动带有3N个模式, 代表面内摇摆(rocking)、扭转振动(twisting)和面间摇摆(wagging). 最后, 在平移带中的光学振动模式为3N— 3个. 这是适用于所有冰相(冰X除外)的一般规律.
3.1 冰Ic理想模型中的两类本征振动
根据冰的B-F构型规则要求, 晶格中的每个水分子都会与四个最近邻分子以氢键相连接[154].因为氢的另一端与氧原子共价结合, 所以这个键通常表示为O—H···O, 且H···O的距离比O—H共价键的要长得多. 与氢共价结合的分子可以称为“供体”, 另一个分子称为“受体”, 每个水分子都可以作为两个氢键的供体和其他两个氢键的受体. 在O周围产生四面体键, 几何上类似于金刚石结构.虽然不同冰相的对称群不同, 但是这种结构存在于所有冰相之中.
首先从氢有序的Ic相入手分析冰的简正振动模式, 冰Ic相红外振动的实验谱与冰的常态相Ih很相似, 在远红外平移振动区也存在两个明显的特征振动峰. 冰的立方相Ic, 其结构经测定是氢无序的. 如果要用计算机模拟的方法研究其红外振动谱, 需要构造一个很大的超胞, 以模拟其内部的氢无序结构. 这样, 利用CASTEP计算时, 虽然把整个超胞看作一个周期性的结构单元, 但内部足够多的氢无序就能够近似模拟实际的情况. 然而这样的话, 所有与氢键振动有关的简正模式都是非简并的, 会有大量的振动频率接近但整体振动情况不一样的振动模式. 这给寻找氢键振动的规律带来了很大的问题. 根据文献, 整体呈现氢无序的Ic相可能主要由铁电有序相等某些不同的有序结构混合构成的[63]. 为寻找隐藏其中的规律, 先抓主要矛盾,就用铁电相的结构作为理想模型进行模拟. 因此,建模了一个有序相的冰Ic结构, 其原胞仅含两个水分子, 这是所有冰相中最简单的结构, 其分子偶极矩朝向相同, 因而具有铁电性. 计算得到的振动谱与实验谱[129,131]十分吻合, 如图3所示. 实验测得的中子散射谱中这两个劈裂的氢键峰位于28和37 meV处, 对应计算谱上的26和35 meV处的两个峰.
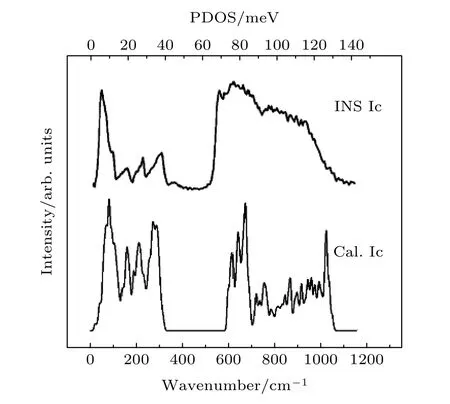
图3 氢有序的冰Ic相的INS谱和PDOS谱, 横轴单位为cm—1(底轴)和meV(顶轴)Fig. 3. INS spectrum and PDOS spectrum of hydrogen ordered Ice Ic, the units of horizontal axis are cm—1 (bottom axis) and MeV (top axis).
如图4所示, PDOS是计算出的第一布里渊区的声子量子态数在能量轴上的分布, 可与INS实验谱相对应. 但积分出的振动峰与Gamma点的简正振动频率并不一一对应.

图4 (a)布里渊区中的声子色散曲线; (b)归一化声子态密度(PDOS). PDOS曲线的纵坐标与图(a)中的纵坐标对应Fig. 4. (a) The Phonon dispersion curves; (b) the corresponding integrated PDOS spectrum.
氢有序相冰Ic原胞中共有6个原子, 因此在图4(a)中有15支光学格波. 仔细观察Gamma点的频率值会分析发现, 在低于500 cm—1的分子间平动区有三个简正振动, 有一个能量在321 cm—1,另两个简并的能量在230 cm—1. 在PDOS谱和实验测量的振动谱中表现为两个特征峰. 再去观察这两类简正振动模式会发现, 这是冰相中最基本的两种振动模式, 我们称之为氢键的四键振动和双键振动两种模式. 四键振动, 即水分子沿着H—O—H的角分线方向振动, 与之相邻的四个水分子则反向振动, 牵动了四个连接的氢键一起工作. 这时分子受力大, 因此对应的能量强、振动频率高. 双键模式则对应能量较低的模式, 分子在垂直于角分线的平面内有两个正交的振动方向, 这两个方向分别对应着两个关联的氢键. 即只有两个氢键参与该分子的平移振动, 而另外两个氢键虽然会有空间角度的变化, 但键长不变. 这样的话, 分子受到的总的弹性回复力弱, 振动能量低, 频率小. 因为两个弱振动的方向具有对称性, 因此能量是简并的. 图5展示了Ic相平动区的三种振动模式, 230 cm—1处为二重简并的双键振动模式, 321 cm—1处为四键振动模式.

图5 氢有序的Ic相理想模型平动区的三种简正模式. 因为原胞仅含两个水分子, 为显示整体的振动情况, 使用了超胞来演示两类振动模式. 绿色箭头表示振动方向, 大小正比于振幅Fig. 5. The three normal modes in the translational region of hydrogen ordered Ice Ic. The primitive cell contains two water molecules, and in order to show the vibration of the whole, the supercell is used to demonstrate two vibration modes. The green arrow indicates the direction of the vibration, and the magnitude is proportional to the amplitude.
根据模拟结果, 波数在230 cm—1处的振动模式具有拉曼和红外活性, 而在321 cm—1处只检测到一个较弱的拉曼实验峰, 没有红外活性. 这就是为什么过去人们只看到一个氢键特征振动峰的原因. 而中子散射不受选择定则的限制, 因此看到了能量更高的那个振动峰, 与模拟结果相吻合. 理想模型中的两种模式振动波数之比即能量比为321/230 = 1.4. 这是氢有序的正四面体结构下的两种本征的振动模式. 常压下, 这个区别十分明显,但高压相中两个特征振动峰变成两个部分交叠的吸收带. 因为高压下正四面体结构变形, 不同冰相的键长键角等呈现一定的分布. 同时因为氢排列的无序性, 振动能量都是非简并的, 这样所有的振动模式即量子态会存在一定的分布区间, 两类模式出现交叠, 使得振动谱呈现为复杂的两个或者多个吸收带, 甚至有的因为红移会与声学支声子交叠在一起. 具体细节后文有详细的讨论. 现在我们依据理想模型, 试图给出一个解析解来理解这两类本征的振动模式.
基于冰的理想四面体结构, 将分子看作质点,先忽略氢的存在, 以氧原子为质心. 可对其晶格动力学进行如下分析. 原子振动的能量为
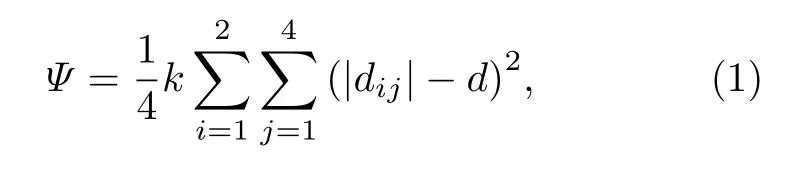
其中k为氢键力常数;d为O—O的平衡间距;(|dij|-d)为相邻两个分子之间的相对位移;i表示一个原胞内的两个分子;j表示四个相邻的分子.1/4是为了减去重复计算的势能. 一个原胞有两个水分子, 故自由度是6. 对于广义坐标, 使用下标α= 1, 2, ···, 6. 将分子位移的势函数作泰勒展开:

l,l′表示不同的原胞. 假设氢键与振动方向的夹角为 c osθ, 振动能量与 c os2θ正比. 由于旋转对称,则有
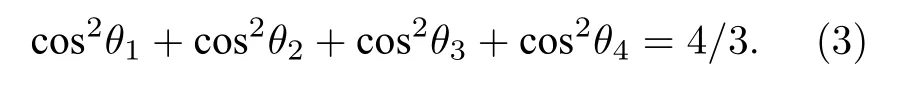
因为事实上存在不同的振动模式, 考虑到力常数会有变化, 并且解析式不能完全表达氢键的量子效应, 在力常数前乘以一个可变系数c, 得到力矩阵:
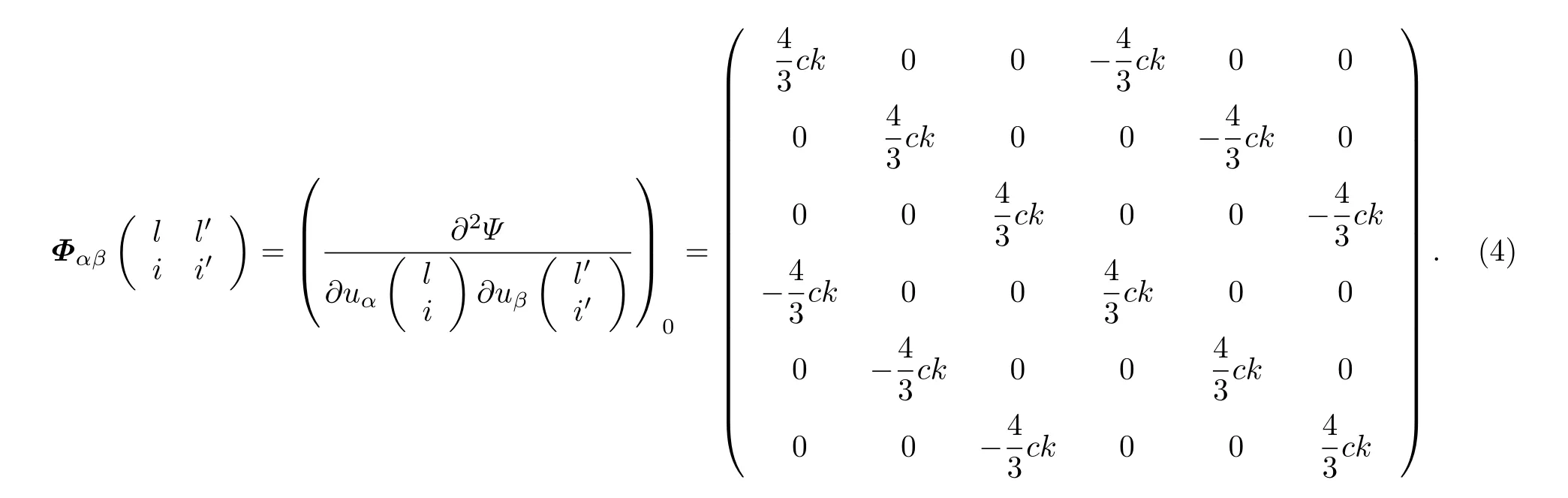
原胞的拉格朗日量为

力常数矩阵表示为

这样, 理想模型下, 我们会得到三个简并的本征值.如果把水分子看作一个质点, 那么其原胞的结构与金刚石是类似的. 一个仅含两个原子的原胞存在3×2-3=3个光学支振动模式. 简单计算一下就知道, 这三个光学支是简并的, 是三个空间正交的振动方向. 由于氢原子的存在, 正四面体的三维对称性被破坏, 出现能量非简并的两类振动模式. 其中一类是强振动, 只沿着角分线的方向, 也是正四面体两条相对棱的中点所确定的方向振动. 这时每个水分子与周围的四个邻居振动方向相反, 因此牵连的四个氢键同时工作, 弹性恢复力大, 振动能量高; 另一类是两个弱振动, 彼此正交, 在强振动方向的垂面内, 沿着其中两个氢键的方向运动, 而另两个氢键没有伸缩变化, 因此相应的弹性恢复力小, 振动能量低. 根据模拟结果, 理性模型下两类氢键振动的具体波数为320.76和229.96 cm—1[139].因此, 得到:

根据文献, 取氢键力常数k=17.1N/m (文献[14],第56页), 会得到可变系数的值为这两个系数的比值为c1/c2=1.95≈2.
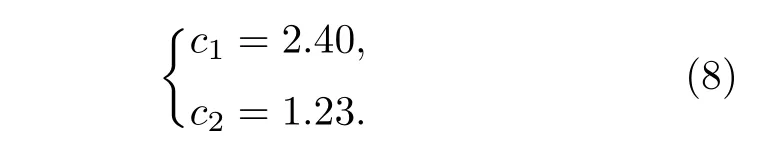
由此验证了四键模式的氢键贡献是双键模式的两倍, 因此振动能量比约为这就证明了我们提出的四键振动与双键振动两类本征振动模式是合理的, 称之为两类氢键理论. 这是关于冰的原子分子振动的新理论, 结合平动区集体振动、非氢键振动等的新认识, 为其分子振动理论补上了最后一块拼图. 接下来我们对不同冰相展开具体的讨论.
3.2 平动区振动的系列研究
3.2.1 氢有序冰相的振动
以Ic相为线索, 首先调研了部分氢有序的冰相, 包括X, VIII, XIII, XIV, XV, II, IX和XI等.图6给出了他们的PDOS谱, 我们发现这些有序冰相中大都存在由这两类氢键振动形成的两个明显的特征峰. 然而, 有些冰相的振动谱却表现出更为复杂的特征. 比如在冰VIII的计算谱中[140], 看起来似乎没有强氢键振动, 而这正是Li[131]在INS实验中观察到的现象. 理论研究表面, 其两类振动仍然存在, 只是因红移与声学支声子交叠到一起了. 对于冰X相, 它没有分子间氢键, 因此不存在两类氢键本征振动模式, 氢键振动区和伸缩振动区在振动谱中消失[141]. 后面会有详细讨论.
在图6中, 我们按照不同冰相环境压强的大小排列PDOS谱. 一般而言, 随着压强的增加, 氢键键长变短, 氢键强度应增强. 但冰VIII和冰XV[142]是个特殊的例子. 这归因于它们特殊的结构, 冰VIII和冰XV皆是由两个子晶格相互套构而成的,子晶格之间没有氢键连接. 尽管随着压强的增加使得冰VIII密度变得很大, 但每个子晶格体积会发生膨胀. 这使得子晶格内部的氢键长度增加到2.038 Å, 比冰Ic相长13.3%; 并且氢氧共价键相应地缩短到0.976 Å, 比冰Ic相短2.4% (具体数值见表1). 这就是冰VIII的氢键振动带发生明显红移而氢氧共价键的伸缩振动带出现大幅蓝移的原因. 表2依次列出了氢键、氢氧共价键的长度和相邻的氧原子的距离, 还有分子间平动、分子间转动、分子内弯曲、分子内伸缩共四个区域的波数范围. 由表2可知, 冰VIII的强氢键最大值红移至254 cm—1, 而分子内的伸缩振动波数最小值则蓝移至3357 cm—1处. 冰XV的最大强氢键波数红移至285 cm—1, 而最小的伸缩振动波数蓝移至3278 cm—1处.
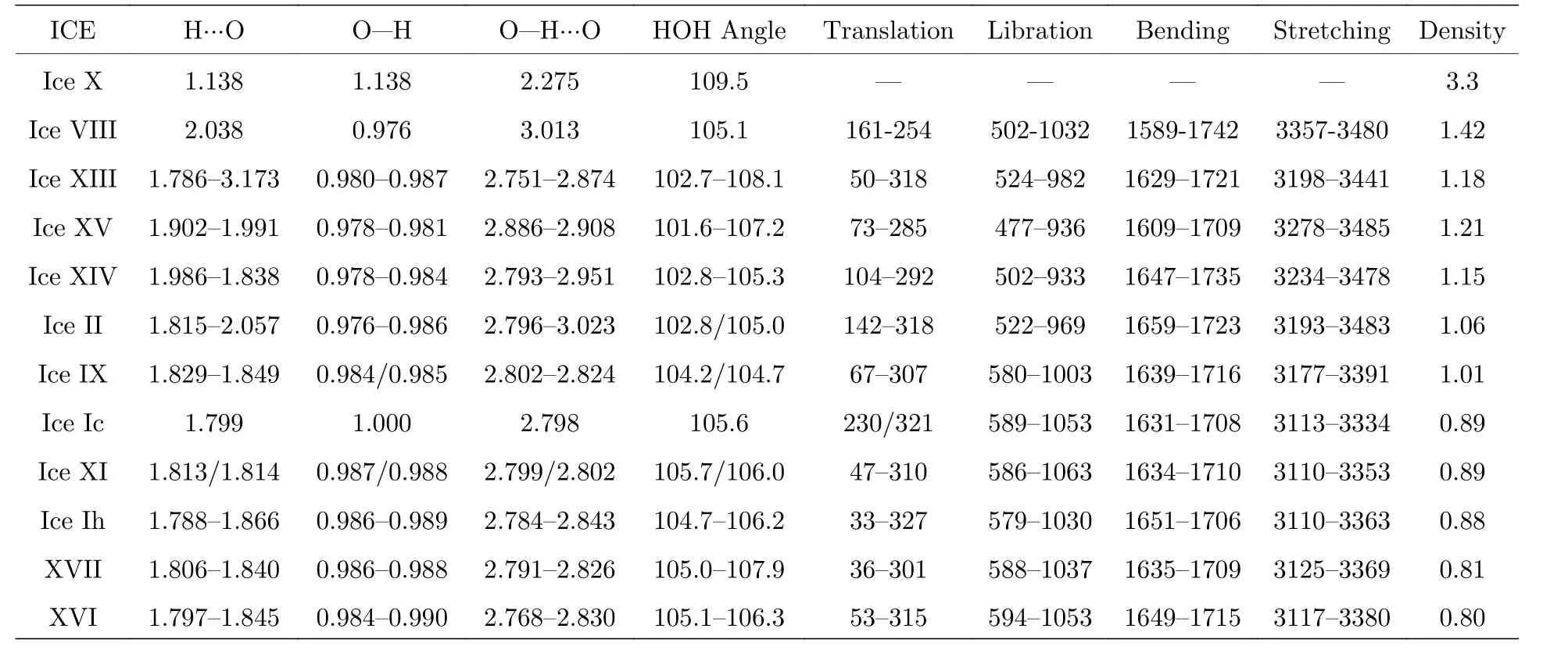
表2 各冰相的氢键、氢氧共价键的长度和相邻的氧原子的距离(单位: Å), H—O—H键角, 4个振动区域的波数范围(单位: cm—1), 结构优化密度(单位: g/cm—3)Table 2. Length of H-bond, OH covalent bond and distance of adjacent O atoms (in Å), H—O—H bond angle, wavenumber range of four vibration regions of ice phases (in cm—1), structure optimization density (in g/cm—3).

图6 氢有序冰相PDOS计算谱, 按照压强大小排列, 从上到下依次是冰X, VIII, XIII, XV, XIV, II, IX, Ic和XI.黄色矩形区域对应两个氢键特征峰的位置Fig. 6. PDOS spectrum of hydrogen ordered Ice phases, arranged by pressure, from top to bottom are ice X, VIII,XIII, XV, XIV, II, IX, Ic and XI. The yellow rectangle region corresponds to the positions of two characteristic peaks of hydrogen bond.
从图6中可以看出, 冰X相的声子态密度谱表现出其非常复杂的物理特征. 通过对冰VIII相加压, 发现该结构最终在120 GPa下完全转变成冰X相. 随着压强的升高, 氢键键长缩短直至消失, 密度变大, 冰VIII逐渐转变成为体心立方相,氢原子位于两个氧原子的中点, 成为类似金属氧化物结构, 不再有分子间氢键. 因此冰X的振动谱与其他冰相截然不同. 作为冰家族中的一个特例, 冰X没有氢键, 因此不存在两类氢键本征振动模式.因为冰X相的周期性结构是由6个原子构成的原胞, 共有 3×6-3=15 个光学简正模式, 3个声学模式. 下面分别讨论这15种简正振动模式. 图7展示了冰X的6个典型的振动模式. 其中450, 998,1260和1508 cm—1波数处的振动模式都具有三个简并态, 2115 cm—1处的振动模式有两个简并态,最大值2623 cm—1处的氢原子中心对称振动模式是非简并的.
对于图7中450 cm—1处的振动模式, 只有氢原子振动, 最大氢原子的振动方向沿着(1, —1, —1),另外两种简并模式的振动方向用(1, 1, 1)和(1, 1,—1)表示. 这是一个红外活性振动峰. 在998 cm—1处的振动模式中, 所有氧原子都在振动, 然而氢原子却在晶格中保持静止. 998 cm—1处的振动是三重简并态, 对应三个正交的振动方向 (0, 1, 0), (1, 0,0)和(0, 0, 1), 而且对压强非常敏感, 随着压强的改变峰值会有较大移动. 这是基于简谐近似下的惟一的一个拉曼活性峰. Putrino和Parrinello[96]报道冰X的拉曼谱有一个约950 cm—1的峰, 这与我们峰值998 cm—1的计算结果是符合的. 此外, Goncharov[97]工作也证实了有一个约在980 cm—1的主要拉曼活性峰, 进一步说明了我们计算结果的可靠性. 在1260 cm—1处的三个转动振动模式, 它们与其他冰相中的转动模式相似. 氢原子垂直于O—O线振动, 且4个氢原子围绕中心氧原子旋转形成类似于涡流的形状. 根据旋转轴的特点可以将这三个简并态大致描述为(1, —1, 1), (1, 1, 1)和(1, 1, —1). 在1508 cm—1处的简并的三种弯曲振动模式, 其中4个O—H—O键向同一方向弯曲(三个键伸缩强, 一个键伸缩弱). 这个三重简并峰构成了红外吸收谱的另一个活性峰. Goncharov等[84]的红外实验可以很明显地看到一个约在1500 cm—1的红外峰. 此外, 他们的计算也表明, 在超过120 GPa的压强下, 存在两个红外吸收峰, 1508 和450 cm—1.这与我们的计算结果非常吻合. 在2115 cm—1处有两个简并模式, 在2623 cm—1处只有一个独立模式.对于第一种2115 cm—1的模式来说, 两个氢原子沿着(1, 1, 1)相反的方向振动, 然而另外两个氢原子沿着(—1, 1, 1)振动. 另一种2115 cm—1的模式可以被看作是一个H—O—H键沿(—1, 0, 0)方向弯曲, 然而另一个H—O—H键沿(1, 0, 0)方向振动.2623 cm—1波数处的振动是一个独特的模式, 具有最高的频率也是最大的振动强度. 在这个模式下,4个氢原子向中心氧原子对称伸缩. 这是一个通过反演中心的对称运动, 因此红外谱和拉曼谱都是非活性的.
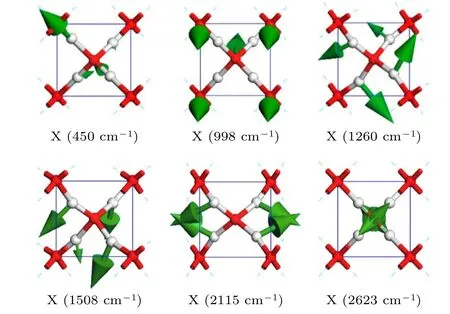
图7 冰X相的简正振动模式, 其中450, 998, 1260和1508 cm—1波数处的振动模式都是三重简并的, 2115 cm—1处的振动模式是二重简并的Fig. 7. The normal modes of ice X, the vibration modes at 450, 998, 1260 and 1508 cm—1 are triplically degenerate, and the vibration modes at 2115 cm—1 are doubly degenerate.
附录A中列举了其他氢有序冰相中两类氢键振动模式的例子. 冰IX[143], II[144]和XIV[145]相的振动谱平动区的最高波数分别为307, 318和292 cm—1,这些振动模式都属于典型的四键振动, 对应其PDOS谱中氢键振动峰的极大值. 冰IX在210 cm—1处的振动模式为双键振动, 具有拉曼活性. 冰II在206 cm—1处的振动模式也是双键振动, 具有红外活性. 根据图6可以看出, 冰II的PDOS谱中明显存在两个氢键振动峰, 位置分别在206和282 cm—1处. 冰XIV的PDOS谱中两个氢键振动峰的中心分别在198和279 cm—1波数处. 总之, II, IX和XIV这几种冰相虽然是高压相, 但两个氢键特征峰还是很明显出现在振动谱中.
3.2.2 氢有序和氢无序冰相的对比研究
通过对比研究氢有序的冰VIII和氧原子位置相同但氢无序排列的冰VII[146], 我们发现氢无序结构也符合两类氢键理论. 在冰相中, 许多相在振动光谱的远红外区域都表现出两个特征氢键峰, 但如图6所示, 冰VIII/VII是一个明显的例外. 图8给出了冰VIII的INS实验谱和PDOS谱, 以及冰VII的PDOS谱.
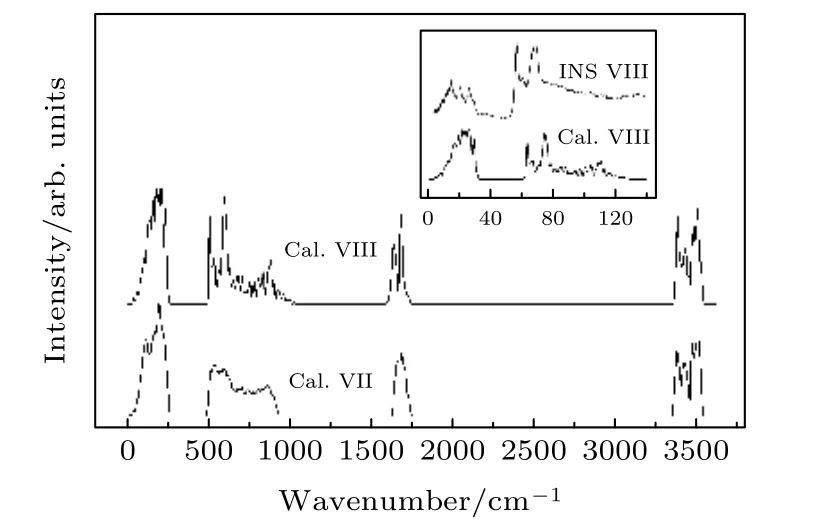
图8 冰VIII和冰VII的PDOS谱对比图. 插图为冰VIII的INS谱和计算得到的PDOS谱, 范围在2—140 meVFig. 8. PDOS spectrum of Ice VIII and VII. The inset shows the INS spectrum of Ice VIII and the computed PDOS spectrum (2—140 meV).
在INS谱中, 冰VIII的平动区可观察到14.7,20.7和26.7 meV处的三个尖峰, 和55.0和68.0 meV处的两个强峰[155]. 在模拟的PDOS谱中, 它们出现在503和593 cm—1处, 相较实验谱表现出一定的蓝移. 通过对比冰VII和VIII的PDOS谱, 我们发现冰VII中没有出现明显的尖峰. 这是因为冰VIII的原始细胞只有4个水分子, 总共有4 ×3 × 3 — 3= 33个光学简正模式; 而冰VII的计算是通过构造一个64个水分子的超胞来模拟的, 共有573个光学简正模式. 这些非简并的量子态能量差很小, 相互耦合在一起, 交叠成一个较平滑的吸收带. 在INS谱中, 冰VIII的分子内伸缩振动在能量为3436 cm—1处出现了一个窄高峰[156], 峰宽比冰Ih要窄得多, 这表明伸缩振动模式之间存在弱耦合.
在Li[131,132]的理论中, 他认为在冰VIII的INS谱中只有一个弱氢键的振动峰, 其强氢键缺失. 然而我们的模拟结果显示, 冰VIII中的两种振动模式都存在. 下面, 我们通过对Gamma点的VII/VIII简正模式的统计分析, 就能证实这个观点.
从图9(a)可以看出, 冰VIII中, 四键振动明显分离, 双键振动与子晶格间的相对振动即非氢键振动混合到一起. 冰VII的三种振动模式分布不是可以直接观察到的, 先把非氢键振动区分出来. 在氢键振动模式中, 按照超胞中振幅最大的分子的振动方向与其对角线的关系来区分两类振动. 为此,我们自编了一个程序来实现对计算数据的自动处理[147].从图9(b)的分布图中看到, 三种振动模式互有交叠. 相对于冰Ic相, 子晶格内氢键距离变大, 相应的振动能量显著红移, 不仅与能量更低的非氢键振动相混合, 而且也会与高频的声学支声子重叠. 因此会呈现出Li实验观察到的谱图. 因此, 我们通过对比分析冰VII与冰VIII的简正模式, 确认两类氢键振动模式存在于这两个冰相之中. 这一发现否定了仅从实验观察得到的结论, 证明了冰VII/VIII中仍存在两类本征的氢键振动模式.

图9 (a)冰VIII和(b)冰VII的双键振动(红色)、四键振动(蓝色)、非氢键振动(绿色)三类模式的分布图. 插图为计算模拟得到的VIII和VII的PDOS谱, 范围0—350 cm—1Fig. 9. Statistical distribution of two-bond vibration (red),four-bond vibration (blue) and non-hydrogen bond vibration modes (green) of Ice VIII (a) and Ice VII (b). The insertation shows the PDOS spectrum of Ice VIII and VII(0—350 cm—1).
我们观察发现冰VIII中的两类氢键振动与冰Ic几乎相同. 波数在237 cm—1处的四键模式,两个子晶格呈反相振动, 与此对应的双键模式在161 cm—1, 强度比为1.47.
我们用同样的方法对比研究了冰Ih和它对应的氢有序相冰XI[147]. 图10给出了冰 Ih 的INS谱和冰Ih、XI模拟谱的对照关系. 此外, 还给出了冰Ic的计算谱便于对比, 它们在远红外区都存在两个特征振动峰.
冰Ih相的INS谱在226和303 cm—1处有两个显著的氢键峰, 这与冰Ic实验谱中两个氢键峰的位置几乎一致. 据报道, 冰Ih, XI和Ic相, 有几乎相同的实验振动谱[131,132], 这与我们的计算结果相符合. 如图10所示, 冰Ih、XI和Ic的计算谱中远红外区都有两个明显的氢键峰, 且位置与实验谱一致. 这三个相的两个氢键振动峰各自位于242/312 cm—1, 204/288 cm—1和208/271 cm—1处.冰Ih为六角形冰, 冰XI为斜方形, 冰Ic为四方晶体结构. 尽管他们的空间群不同, 但有着相同的密度, 即相同的氢键键长. 因此, 振动峰的位置也大体一致.

图10 从上到下依次是冰Ih相的INS实验谱和模拟的PDOS谱, 冰Ih对应的氢有序相冰XI的PDOS谱, 理想模型Ic的PDOS谱Fig. 10. The INS spectrum and PDOS spectrum of ice Ih,the PDOS spectrum of hydrogen ordered ice XI and the PDOS spectrum of ice Ic.
冰XI的一个原胞中有4个水分子, 因此在平移带中共有9种振动模式. 在47, 52和168 cm—1处的振动模式是相邻分子层沿y轴、x轴和z轴的相对平移运动, 能量较弱. 两个简正模式在310和308 cm—1的是强氢键振动, 对应于Ic在321 cm—1处的四键振动; 在210, 220, 225和229 cm—1的四种弱氢键振动模式对应于Ic在230 cm—1处的双键振动. 这两类氢键振动能量的平均比值也是1.4.附录A中给出了冰XI在220和310 cm—1处的振动模式, 分别对应双键振动和四键振动.
拟合了冰XI/Ih相中Gamma点的两类氢键振动模式的分布, 范围在200—320 cm—1之间, 如图11(a)所示. 插图为模拟的PDOS谱, 作为对照.

图11 (a)有序相冰XI和(b)冰Ih的双键振动、四键振动模式的统计分布图. 插图为计算模拟得到的XI, Ih的PDOS谱Fig. 11. Statistical distribution of two-bond and four-bond vibrational modes of (a) ice XI and (b) ice Ih. The illustration shows the PDOS spectrum of XI and Ih.
因为有色散曲线, 实际的PDOS谱比Gamma点分布要复杂. 图11(a)插图中冰XI的两个主峰明显来自这两种振动模式. 在冰Ih中两类振动的重叠主要原因有: 1) 自编的区分两类振动模式的程序以氧为分子质心带来的系统误差; 2) 氢键键长不是定值, 有一个分布, 使得两类振动都有一定分布区域; 3) 氢无序排列带来的键长键角的变化使得正四面体结构对称性的改变引起的两类振动模式有一定的耦合态. 此外还要注意, 在远红外区除了两类本征振动外, 还有分子团簇的振动以及非氢键的振动, 这些能量更低; 还有高频的声学支声子会与低频光学支声子耦合, 仔细观察图4中Ic的色散关系, 可以看到平动区光学支中的低频声子与声学支的高频声子叠加出一个比四键振动、双键振动更低的峰. 这个Ic的峰在图10中看得比较清晰, 在Ih和XI中也存在.
同样对比研究了冰XIII[148]/V和冰XV/VI的情况. 图12给出了它们的PDOS谱, 同时给出了冰VI, V的INS谱便于对比.
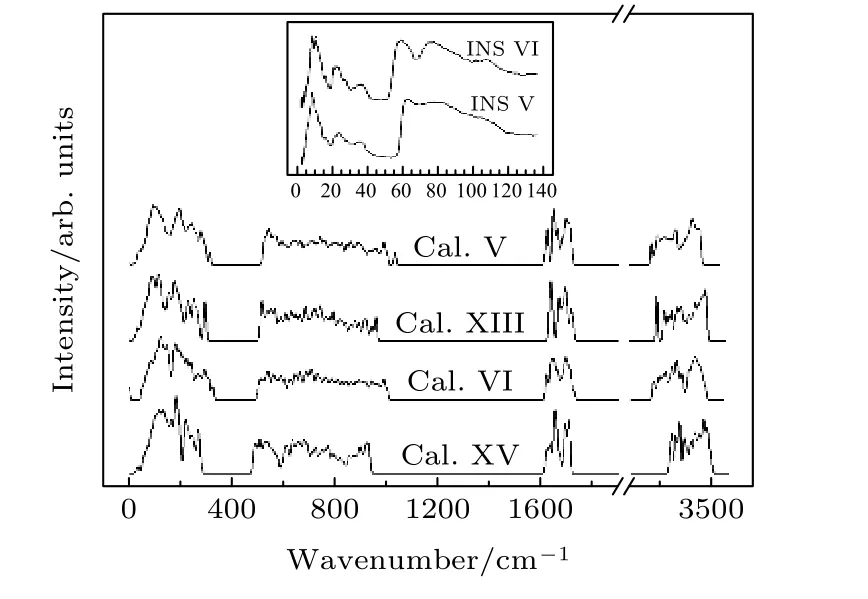
图12 冰V/XII和冰VI/XV的PDOS谱对比图. 插图为冰VI和V的INS谱, 范围2—140 meVFig. 12. Comparisons of PDOS spectrum of Ice V/XII and Ice VI/XV. The insertation shows the INS spectrum of ice VI and V (2—140 meV).
图12 可见, 这些高压相的谱显得比较复杂,两个振动峰不是很明显. 由于高压使得冰的局域正四面体结构变形, 冰XIII/V中不再是六环结构而是出现了四环结构, 其四环内的键长键角与四环间的有很大不同. 这导致了强、弱氢键都出现分裂,两类氢键振动互相交叠在一起, 主要分布在振动谱200—300 cm—1之间. 我们通过比较冰VI的PDOS谱和INS谱, 发现Li等[88]报道的实验峰在172.3, 191.6, 230.2和300.2 cm—1处, 这与振动谱中179.5, 193.2, 236.6 和294.6 cm—1波数处的峰值还是相一致的. 冰XV/VI的结构是由子晶格相互套构而成的, 因此在平动区的最低频率处还存在一些非氢键振动, 后面会继续讨论.
综上所述, 除了冰X相外, 由于局域的正四面体结构, 氢有序和无序冰相, 都存在两类本征的氢键振动模式, 并在很多冰相中形成了远红外区两个明显的氢键振动峰. 这个规律普遍适用于所有冰相, 称之为两类氢键理论.
3.2.3 团簇振动或晶格骨架变形振动
除了两类氢键振动, 平动区还有能量更低的一些振动模式, 比如团簇的振动和骨架变形振动. 由于参与振动的分子数多, 而氢键相对少, 振动能量偏低. 像前面提到的冰VII/VIII结构, 是由两个子晶格嵌套而成的, 两个子晶格之间的相对振动是非氢键振动. 这些振动声子会形成能量更低的波包甚至与声学支声子交叠到一起.
其中, 冰VIII的结构由两个冰Ic相晶格反向嵌套而成, 冰XV也是由两个相同子晶格反向嵌套而成. 在冰XV中, Whale等[75]发现在66, 78和85 cm—1处对应着两个子晶格之间的相对振动, 他们称之为“刚性网络”振动模式. 而我们的模拟结果分别对应73, 106和107 cm—1处, 它们实际上代表了三维空间中的三种相对运动. 由于两个子晶格之间没有氢键连接, 因此它们的振动能最低. 例如图13中冰XV在107 cm—1处的振动模式.
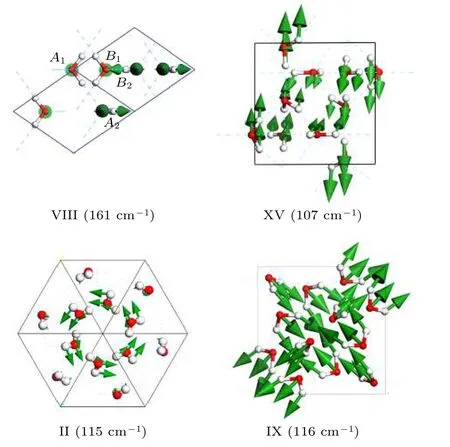
图13 冰VIII平动区161 cm—1处的简正振动和冰XV在107 cm—1处的振动; 冰II平动区115 cm—1处的简正振动和冰IX在116 cm—1处的振动示意图Fig. 13. The normal mode at 161 cm—1 in ice VIII and 107 cm—1 in ice XV; The normal mode at 115 cm—1 in ice II and 116 cm—1 in ice IX.
冰II和IX中的团簇振动是以多个水分子团的方式集体振动的. 例如冰II中6个分子成环以相同的方式振动, 它们内部的氢键不参与振动. 因此冰II的团簇振动对应的振动频率低于两类氢键振动, 对应着平动区能量最低的9种振动模式.
综上, 平移振动带的振动波数低于400 cm—1,可以把振动模式分为三类: 1)四键振动; 2) 双键振动; 3)团簇振动或非氢键振动. 有的团簇振动呈现为晶面层之间的振动或整个晶格骨架的弱振动. 根据以上分类, 我们大致可以厘清冰在远红外区的吸收带的构成. 过去人们对于冰晶格中水分子的振动并没有远红外区的详细讨论. 以上研究填补了这块空白, 尤其是两类氢键理论的提出, 解释了两个特征振动峰的来源.
3.3 其他振动带的讨论
3.3.1 转动振动
关于水分子的转动振动, 人们已经有了清晰的认识. 对于冰相的分子间转动振动带, 有3N个简正振动模式分布在波数从400到1100 cm—1左右.这个区域的分子转动模式可以分为三种类型: 面内摇摆(rocking), 面间摇摆(wagging)和扭曲转动(twisting). 面内摇摆是指在水分子平面内摆动, 即整个分子绕垂直于分子平面的轴转动; 面间摇摆是指绕水分子平面内垂直于H—O—H角分线的轴摆动; 扭动是指分子绕着H—O—H角平分线的轴来回转动.
我们以单个水分子为例, 解释三种不同的振动模式. 如图14所示, 以水分子所在平面为yz平面,以氧原子质心为原点, 以HOH角平分线所在方向为z轴. 因此, 水分子沿x轴转动是面内摇摆, 沿z轴转动是扭曲转动, 沿y轴旋转则是面间摇摆.因为水分子转动时具有很小的转动惯量, 所以呈现出复杂交叠的转动振动谱.

图14 在直角坐标系下yz平面内展示水分子的三种转动 (a)绕z轴的扭曲转动; (b)绕y轴的面间摇摆; (c)绕x轴的面内摇摆Fig. 14. Three rotations of H2O: (a) Twisting around the z-axis; (b) wagging around the y-axis; (c) rocking around the x-axis.
我们讨论Gamma点的光学支简正振动. 当分子振动时, 原胞的质心需要保持静止. 随着波数的增加, 转动区的振动模式往往是这三种类型的组合. 在转动带的最低波数处, 水分子的振动模式为面内摇摆, 中间波数处的主要振动模式为面间摇摆或几种振动模式的组合, 扭曲转动的转动惯量最小, 波数最高.
3.3.2 弯曲振动
弯曲振动带的简正模式数最少, 只有N个. 每个分子的振动类型都是键角开合的弯曲振动, 即键长不变只有键角发生变化. 我们根据不同分子的相位差可以将其分为两类: 同相振动和反相振动. 同相振动是指所有分子振动相位相同, 在图像上表现为水分子的键角同时开合; 反相振动是指分子振动相位相反, 即一个分子的开的同时另一个分子合.
随着波数的增加, 冰相中振动模式的变化并不相同. 比如在冰XIII和XV等相中, 随着波数的增加, 振动模式由反相振动过渡到同相振动. 而在冰XI等相中, 振动模式由同相过渡到反相. 一般而言, 同相的弯曲振动模式对应的能量低, 而反相振动则对应更高的能量. 在氢无序冰相, 比如冰XVII/XVI中, 集体的弯曲振动很难保持一致, 因此弯曲带的振动往往是两种模式的混合.
3.3.3 伸缩振动
波数高于3000 cm—1的伸缩振动带含有2N个简正模式, 是分子内氧氢共价键的伸缩振动, 分为对称和非对称伸缩振动两种. 水分子中的两个氢氧共价键沿着O—H的方向伸缩, 键长同步变化的称之为对称伸缩振动. 反之, 水分子中的两个氢氧共价键分别沿着成键方向一伸一缩的振动模式, 称为非对称伸缩振动.
对应伸缩带频率较低处, 分子全部表现为对称伸缩振动模式. 而在较高的波数下, 分子主要呈现为不对称伸缩振动模式. Whale等[75]发现一些振动模式似乎只包含一个O—H键的孤立振动, 而另一个则完全不动. 他们认为发现了一种新的振动模式, 命名为“孤立伸缩振动”. 我们在众多冰相中都发现了这类振动, 比如冰II, VII, VIII, XIII, XIV,XV, XVI和XVII. 我们认为, 这种“孤立伸缩”应该是非对称伸缩模式的一个特例, 并把它归因于压强和氢无序晶格引起的正四面体对称性变形的原因. 对于一个多分子晶胞的集体振动, 为保持质心不变, 因为结构的非对称性, 会出现一些类似的振动以协调整体的振动状态.
3.4 笼型冰XVII/XVI的研究
深入研究发现, 两类氢键理论对于形成可燃冰的笼型冰结构也适用. 图15给出了两种笼型冰XVII[149]/XVI[150]的PDOS谱, 并与冰Ih的INS谱进行了对比. 我们发现三者谱线的主要特征十分相似, 因为冰XVII/XVI的氢键稍长, 所以氢键振动的能量偏弱.
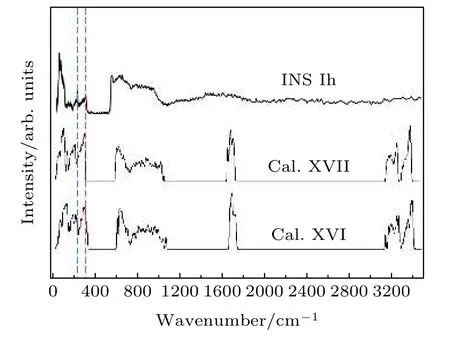
图15 冰Ih相的INS谱和冰XVII, XVI的PDOS谱. 蓝红两条虚线标记出冰Ih相实验谱两个氢键振动峰(226和303 cm—1)的位置Fig. 15. INS spectrum of ice Ih and PDOS spectrum of ice XVII and XVI. The blue and red dotted lines mark the positions of the two hydrogen bond vibration peaks (226 and 303 cm—1) in ice Ih.
冰XVII相也被称为S-I型笼型冰, 是主要的可燃冰结构, 客体分子主要为甲烷、乙烷等天然气成分. 该结构可以没有客体分子而稳定存在. 我们建模了48 个水分子的氢无序冰XVII超胞. 根据模拟结果, PDOS谱中的峰与INS谱的峰相吻合.如图15所示, 冰XVII/XVI的两个氢键特征峰峰值分别位于204/204 cm—1和295/292 cm—1处, 这与冰Ih的INS谱中位于226和303 cm—1处的两个峰相对应.
作为低密度冰相, 冰XVII/XVI的密度比冰Ih/XI的密度低了10%左右. 因此, 与Ih相比, XVII中较长的分子间距离导致偏弱的氢键振动频率和较强的分子内氧氢共价键. 根据统计, XVIl和Ih的氢键平均键长分别为1.827 Å和1.816 Å. 反映在振动谱上, 冰XVII/XVI的平移区最强峰比Ih分别红移了26 cm—1和12 cm—1, 伸缩区则相对蓝移了15 cm—1和7 cm—1.
建模的冰XVI(S-II型笼型冰)由34个水分子构成, 其氢原子是也无序排列的. 其中, 28个水分子组成一个笼子. 晶胞共含有12个五元氢键水环和4个六元氢键水环, 记作51264. 统计了160—320 cm—1区间内双键振动和四键振动的分布, 结果发现220 cm—1处的峰主要由双键振动引起, 而310 cm—1附近的峰主要由四键振动引起, 也符合两类氢键的理论. 综上可知, 两种主要的可燃冰结构中同样存在两类氢键振动构成两个远红外特征振动峰的规律.
在PDOS谱中, 209和301 cm—1波数处的振动模式分别对应冰XVII相中的双键和四键振动, 220和314 cm—1波数处的振动模式分别对应冰XVII相中的双键和四键振动(见附录A). 两者波数之比为1.44和1.43, 与理论模型的略有偏差.
3.5 冰的两个氢键振动峰与液态水吸收带
我们的调研发现, 液态水在远红外区也有两个主要的吸收带. 一个是分子平动, 另一个是分子转动. 其转动带能量有所红移, 覆盖了冰的平动区与转动区的带隙. 由于不能形成稳定的正四面体结构, 不存在两类氢键振动模式, 其平动区的主要吸收带能量低于冰的氢键振动. 如图16所示, 水的平移振动和转动吸收带存在一个波谷, 恰好位于冰Ih 的两个氢键振动峰的位置. 分子振动对红外辐射的能量可产生共振吸收, 如果提供两个氢键振动频率的远红外辐射波段, 或者两束太赫兹激光(能量在 6.8和9.1 THz 左右), 将引起冰相中氢键的共振吸收并能减少能量在液态水中的损失, 使氢键断裂从而实现冰的快速融化. 因为这个位置的能量对活细胞是无害的. 这个设想不仅可以应用于食品解冻、工业除冰等领域, 或许也可以在生物大分子冷冻塑性上有应用价值. 前提是太赫兹激光器的研发能在功率和频率上满足要求. 更远的前景是冰融化释放甲烷从而实现对可燃冰的开采.

图 A1 氢有序冰Ic相原胞及其两类氢键振动模式Fig. A1. Two kinds of H-bond vibrational modes in ice Ic.

图 A2 氢有序冰相IX、II和XIV中两类氢键振动模式. 波数在245, 206和194 cm—1处的振动分别为冰IX, II和XIV的双键振动模式; 波数在307, 318和292 cm—1处的分别为冰IX, II和XIV的四键振动模式 (冰XIV中振动明显的分子用黄色标记)Fig. A2. Two kinds of H-bond vibrational modes in ice IX, II, and XIV. The two-bond vibrational modes of Ice IX, II and XIV at 245, 206 and 194 cm—1 are respectively; The four-bond vibrational modes of ice IX, II and XIV at 307, 318 and 292 cm—1, respectively(The yellow moleculars vibrate obviously in ice XIV).

图 A3 冰VII相在178 cm—1处的双键振动模式和在255 cm—1处的四键振动模式; 冰XVI相在160 cm—1处的双键振动模式和在237 cm—1处的四键振动模式 (冰VII中振幅明显的分子用黄色标记)Fig. A3. Two-bond vibrational mode at 178 cm—1 and four-bond vibrational mode at 255 cm—1 in Ice VII phase; two-bond vibration mode at 160 cm—1 and four bond vibration mode at 237 cm—1 in ice VIII (The yellow moleculars vibrate obviously).

图 A4 冰XI相220 cm—1处的双键振动模式和310 cm—1处的四键振动模式; 冰Ih相244 cm—1处的双键振动模式和327 cm—1处的四键振动模式Fig. A4. Two-bond vibrational mode at 220 cm—1 and four-bond vibrational mode at 310 cm—1 in ice XI; two-bond vibrational mode at 244 cm—1 and four-bond vibrational mode at 327 cm—1 in ice Ih.
图 A5 冰XIII相和冰V相在223/225 cm—1处的双键振动模式和318/312 cm—1处的四键振动模式; 冰XV相和冰VI相在206/231 cm—1处的双键振动模式和285/328 cm—1处的四键振动模式 (冰VII中振幅明显的分子用黄色原子标记)Fig. A5. Two-bond vibrational mode at 223/225 cm—1 and four-bond vibrational mode at 318/312 cm—1 in ice XIII/V; two-bond vibrational mode at 206/231 cm—1 and four-bond vibrational mode at 285/328 cm—1 of ice XV/VI (The yellow moleculars vibrate obviously).

图 A6 冰XVII相209 cm—1处的双键振动模式和301 cm—1处的四键振动模式; 冰XVI相220 cm—1处的双键振动模式和314 cm—1处的四键振动模式 (振幅明显的原子振动用黄色标记)Fig. A6. Two-bond mode at 209 cm—1 and four-bond mode at 301 cm—1 in ice XVII; two-bond mode at 220 cm—1 and four-bond mode at 314 cm—1 of ice XVI (The yellow moleculars vibrate obviously).

图16 水与冰Ih的红外吸收谱对比图Fig. 16. Infrared absorption spectrum of water and ice Ih.
4 结 论
传统上, 标定指纹区的振动峰是很困难的. 通过基于第一性原理的密度泛函理论分析了冰相的简正振动模式. 分子间平移振动带, 波数在0—400 cm—1之间, 我们把振动模式总结为三类: 1) 氢键的四键振动; 2) 氢键的双键振动; 3) 多分子集体振动或非氢键振动. 能量最低的一类振动模式, 如团簇振动或晶面层之间的相对振动等, 由于内部的氢键没参与振动, 对应的振动频率要低于前两类单分子的氢键振动. 冰II、冰IX中的团簇振动是水分子成多元环的集体分子振动, 如冰II中的团簇振动就是以六个分子成环以相同的方式振动的.冰VII/VIII, XV/VI的结构, 是由两个子晶格嵌套而成, 子晶格之间没有氢键, 比如冰VIII的结构由两个冰Ic相晶格反向嵌套而成. 它们平动区最低振动模式表现为两个子晶格之间的相对振动. 四键振动, 是水分子沿角平分线的振动, 牵动了四个关联的氢键振动, 对应的能量最高; 双键振动, 只有两个氢键参与振动, 振动能量低于四键振动模式.根据以上原则, 可以分析不同冰相的远红外区的平移振动模式. 结合模拟结果, 理论上论证了两类氢键振动频率的比约为1.4, 强氢键振动的恢复力常数是弱氢键振动的2倍, 说明四键振动和双键振动的解释是合理的. 通过系统研究冰相中平动区的振动模式, 我们揭示了两个氢键振动峰的来源, 这是对于冰相中氢键振动的一个新理论, 填补了冰原子分子振动的理论空白.
由于液态水没有稳定的局域正四面体构型, 不存在这两个特征峰, 因此在这个位置的远红外能量吸收没有那么强烈我们由此提出, 可以利用远红外辐射的方式, 使得氢键共振吸收, 能在加速冰融化的同时减少液态水对能量的吸收. 这个设想前景可用于食品解冻、工业除冰、天然气管道冰堵、生物大分子冷冻塑型等广阔的领域.
附录A
