小图形 大智慧
——数形结合思想在小学五年级数学教学中的实践应用
2021-08-05徐金燕
徐金燕
(福建省厦门第二实验小学 361009)
数学是研究数量关系和空间形式的科学,“数”和“形”是数学研究的两大对象,两者互相依存,不可分割.抽象的数量关系常常有直观的几何意义,直观的几何性质也常常需要准确的数量关系描述.在研究数学问题的时候,数和形完美的配合,可以准确的把握题目中条件和结论之间的联系,既有几何的直观,又有代数意义的准确.因此,教师在教学,以及帮助学生分析题目时,可以利用数形结合,使得教学更形象直观,也渐渐把数形结合的思想植入学生的思维中.
一、以形助数,帮助学生建立数量关系
当题目中的文字信息比较多的时候,可以适当的画图,利用图形的直观性,帮助学生理解题意,分析数量关系,使抽象的问题变得具体.
例如人教版《简易方程》这一单元的习题:猎豹是世界上跑的最快的动物,速度能达到110km/h,比大象的2倍还多30km.大象最快能达到每小时多少千米?
这道题里的两个量,大象的速度和猎豹的速度,可以先找到“1倍数”,然后再找多倍数和它的关系.教师可以让学生找到后,自己用图表示出来两者的关系,最后可以在板书上画图如图1.

图1
学生通过直观地线段图可以列出方程:2x+30=110.
又如:甲乙两车分别从A、B两地同时出发,相向而行,经过1.5小时在离中点18千米处相遇.已知甲车的速度是乙车的1.2倍,相遇时,两车各行驶了多少千米?
解这道题时,学生会设乙车的速度为xkm/h,则甲车的速度是1.2xkm/h,然后误以为甲车比乙车多走了18千米,从而列出错误的方程.实际上,如果画图出来,这道题的等量关系很好找出来,如图2.

图2
读图就可以知道,甲其实比乙多走了两个18km,等量关系就是“甲的路程-乙的路程=18km×2”,进而可以列出方程:1.2x·1.5-x·1.5=18×2.
以数解形,帮助学生建立图形观念.还有一种类型的图形题,学生不动手画,只靠凭空想象,或者是画了图,但是没有结合准确数据,导致解题错误.
例如:在一个长20厘米,宽4厘米的长方形纸条里剪出如图3所示梯形,最多能剪几个?
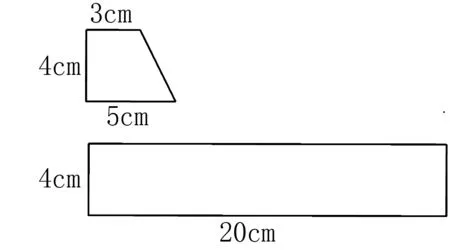
图3
很多学生直接算出长方形的面积S长=4×20=80cm2,再算出梯形的面积S梯=(3+5)×4÷2=16cm2,然后算出80÷16=5(个).然而,这道题经过画图就会发现根本剪不了5个,如图4.

图4
这样剪完4个直角梯形后,剩下的部分虽然面积也有16平方厘米,但是不能再剪成满足题意的图形.因此,此类题目不是大面积除以小面积就可以的,一定要结合图形来画一画.
另外一种题目是虽然学生画了,但是因为对题目规律的理解不深刻,也导致题目做错:在长7.2分米,宽1分米的长方形卡纸上,剪出底是1.2分米,高是1分米的等腰三角形(如图5),最多能剪出几个?

图5
有了之前的经验,学生知道考虑边长了,通过7.2÷1.2=6(个),算出一面可以剪6个,但是接下来错误的以为另一边也可以剪6个,直接得出6×2=12(个).但是通过数据进行画图可以知道,因为有两头的损耗,剩下的另一边只能剪出6-1=5(个),所以总共是11个这样的三角形(如图6).

图6
在整个教学过程中,通过以数想形的思想,学生从单纯的计算和观察转化到一边画一边结合数据想,并且提炼出相应的抽象规律.因此,在分析数学题目时,数和形缺一不可.在此过程中,锻炼了学生的观察能力,实际动手操作能力,还有想象能力.
此外,在学习植树问题的时候,也可以通过数形结合,用画图的方式,让学生感受到树和间隔的一一对应关系,如图7.
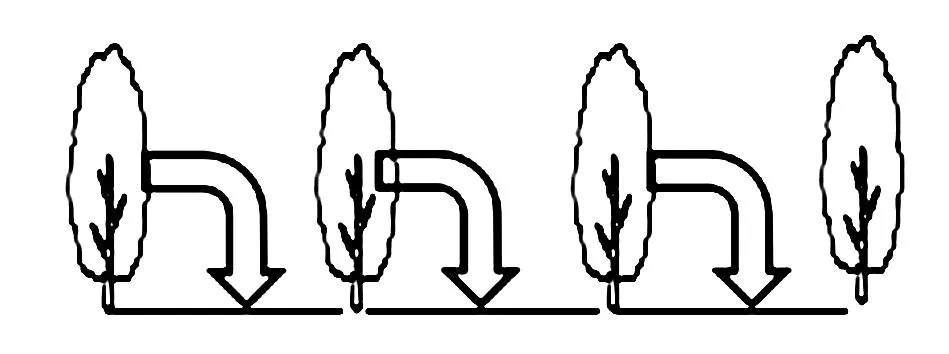
图7
这样就可以不用死记公式,通过简单的画一画知道,当只种一端时,树和间隔正好一一对应,所以,棵数=间隔数.当两端都种的时候,多出的一棵树没有间隔与之对应,棵数=间隔数+1,以此类推.
二、数形结合,提高学生解题能力
在解决数学问题时,同时利用以形助数,以数解形,达到数形互译,将题中的数字信息在图中标注出来,再利用图形的直观,帮助分析各个量之间的关系,从而解决问题.五年级数学上册的《平面图形的面积》这一单元,就对数形结合的应用非常广泛,如果只是单靠看题中的信息,或者单靠看图,是没有办法准确的解决问题的.
例如:如图8,组合图形是由一个正方形和一个三角形组成,已知正方形周长是12cm,求这个组合图形的面积.
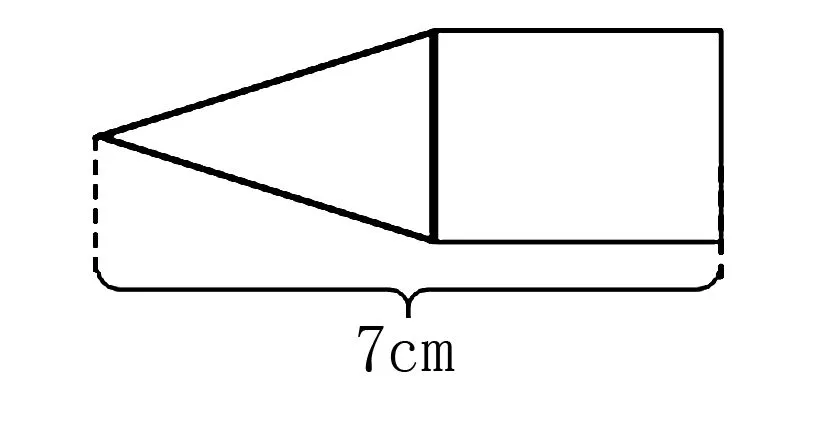
图8
这道题应该先求出正方形的边长是12÷4=3cm,接下来用7-3=4cm,求出三角形的高,而这条高对应的底正好是挨着正方形那条边,也就是3cm,但是教学中发现学生在求出4cm之后,就认为三角形的边长就是4cm,从而使题目做错.归咎其原因,就是没有把题中信息和图结合在一起.因此在教学这一单元的知识的时候,教师要引导学生做标注,比如把知道的线段长准确的标在图中相应位置,接着对图形进行分析,分析的过程中也要结合数据.
根据前面一系列的研究可以得出,数形结合不但是解决问题过程的一个体现,也体现了学生将抽象思维和形象思维结合在一起共同协作的过程.有了形象思维的支持,抽象思维变得更具体明了,使解决问题变得更加简单.数形结合方法也是人们研究和解决问题时,利用数据的精确性和图形的直观化采取的利于问题简单解决的策略和方法.
