核心素养下的初中函数教学策略研究
——以“二次函数”教学为例
2021-08-05张青
张 青
(广东省中山市东区松苑中学 528400)
《普通高中数学课程标准(2017 年版)》提到在高中要培养学生的数学核心素养是:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.初中数学核心素养应该注重培养这六大能力,函数是初中数学教学的重点和难点,翻阅《义务教育数学课程标准(2011年版)》(以下简称《标准》)第一模块《数与代数》中的函数,初中涉及到的函数包含一次函数、二次函数、反比例函数.课标要求:“通过函数知识的学习,学生应该掌握函数的基本概念、性质以及蕴含的基本数学思想方法,并提高学生的抽象概括、逻辑推理、数学建模、数据处理等基本能力.”函数知识的学习对于培养学生的数学抽象能力、逻辑推理能力、直观想象能力、数学建模能力、数据分析能力至关重要,二次函数是函数教学的重点和难点,本文以“二次函数”为例,从核心素养视角下谈谈函数的教学策略,提高初中教学质量.
一、加强概念教学,整体把握本质,激发内在动力
著名数学家华罗庚指出:“新的数学方法和概念,常常比解决数学问题本身更重要.”函数的概念出现在《数学》人民教育出版社八年级下册《19.1函数》这一章节中,以往的教学实践中发现学生看到函数这个名称“望而生畏”,觉得函数这个词语比较抽象,难以理解,也就没有动力学习接下来的三大函数知识,如何激发学生学习函数的内在动力,是学好函数知识的关键所在,其实学生在小学阶段实际问题中就接触过函数模型,只不过到了初中才知道“函数”这个名称,函数的概念起始课至关重要,笔者设计了学生熟悉的问题引入函数的概念.
问题:汽车以50km/h的速度匀速行驶,行驶路程为skm,行驶时间为th.填写表1,s的值随t的值变化而变化吗?
设计意图:从学生熟悉的实际问题出发,揭示函数概念的本质,在这个变化过程中,有两个变量s、t,对于t每一个确定的值,都有唯一的s与之对应,s就是t的函数,函数就是刻画变量之间对应关系的模型,在我们实际问题中很多都能找到这样的对应关系,我们都可以用函数表达.
在函数概念教学的过程中,让学生用整体的眼光看待数学知识,初中学过的三大函数(一次函数、反比例函数、二次函数)都能在实际问题中找到模型,都是这种对应关系,刚开始学生接触函数,教师应该让学生了解初中需要学习的三大函数;教师要从整体的角度进行教学设计,在设计二次函数的教学时,把握函数的本质,二次函数也是这种对应关系y=ax2+bx+c(a,b,c是常数,a≠0),对于每一个x,都有唯一的y与它对应;教师要从整体的思维开展教学流程,每次进行三大函数的教学时,都要回顾函数的概念,加强概念的教学,建立函数的模型,课程结束也要回归到函数的概念,遵循的原则是总-分-总,从整体上揭示函数的本质,激发学生学习函数的兴趣,提高课堂效率.
二、巧用几何画板,注重数形结合,探索函数性质
“几何画板”是一个很好的作图和实现动画的辅助教学软件,在探索函数的性质时,巧用几何画板,结合图像探索性质,用数形结合的思想方法,可以直观深入的讨论二次函数的图像和性质.
1.二次函数y=ax2(a≠0)的图像和性质
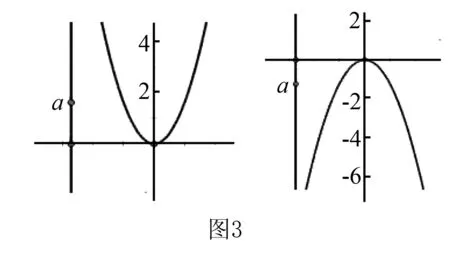
函数的图像和性质是学生深刻认识函数的重要途径,巧用几何画板,可以分别从二次函数的开口方向、对称轴、顶点、增减性等方面进行探索和研究.以y=x2为例,学生从简单的二次函数进行探索,通过列表、描点、连线,学生容易犯的错误就是连的是线段(如图1),根据学生以往的认知发展规律,学生很难理解函数的图像是一条光滑的曲线,借助几何画板,尽可能多选几个点(如图2),学生直观的感受函数的连续性,把数和形结合起来,直观的感受二次函数的图像是一条无限延伸的抛物线,感受函数的定义域是全体实数.

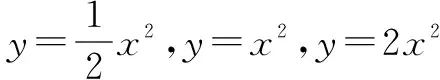
2.二次函数y=a(x-h)2+k(a≠0)的图像和性质
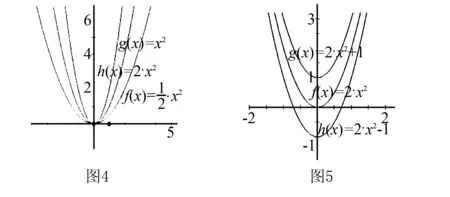
学生已经对二次函数y=ax2(a≠0)的图像和性质有了一定的认识和了解,教师采用特殊到一般的方法,学生通过描点、列表、连线感受y=2x2,y=2x2+1,y=2x2-1三个函数图像的区别和联系(如图5),学生通过列表初步感受当x相同时,y值大1或者小1,几何画板演示三个函数图像,从点的坐标上来看,当x相同时,点向上或者向下平移1个单位长度,从函数图像上来看,图像整体向上或者向下平移一个单位长度,仿照y=ax2的图像和性质,学生很快熟悉了y=ax2+k的图像和性质;同理教师通过几何画板直观演示y=2x2,y=2(x+1)2,y=2(x-1)2的图像和性质,通过数形结合从特殊到一般的数学思想方法,学生熟悉了二次函数y=a(x-h)2的图像和性质,通过不同的平移方法,对比归纳总结出二次函数y=a(x-h)2+k(a≠0)的图像和性质.
3.二次函数y=ax2+bx+c(a≠0)的图像和性质
三、擅用思维导图,引导类比分类,构建知识网络
二次函数与一元二次方程的关系是教学的重点和难点,当二次函数的因变量y为定值时,二次函数就变成了一元二次方程,当y为0时,反应在函数图像上就是二次函数y=ax2+bx+c与x轴的交点,交点的横坐标就是一元二次方程ax2+bx+c=0的解,根据学生以往的知识经验,一元二次方程的解跟根的判别式Δ=b2-4ac有关,一元二次方程的解的个数跟二次函数图像与x轴交点的个数是一一对应的,学生在学习这部分内容时,内容比较多容易混淆,难以突破教学难点和学生的思维障碍,教师在教学过程中引导学生学会画思维导图,把二次函数与x轴交点的个数与一元二次方程根的情况之间的关系进行分类、对比、归纳,借助判别式Δ构建知识网络,提升数学思维,更深刻的理解数学知识.
四、注重函数运用,发散数学思维,建立函数模型

《标准》中指出:“重视学生已有的经验,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程.”在学习二次函数这节内容时,注重函数运用,寻求一题多解,建立函数模型,培养学生数学建模能力至关重要,以人教版《义务教育教科书·数学》九年级上册第二十二章第三节“实际问题与二次函数”(第1课时)的探究题为例(如图6),学生从生活中的实际问题出发,找出篱笆围成场地的面积与一边长之间的函数关系,构造数学模型,利用函数的性质解决问题,寻求不同解决问题的办法,发散数学思维,具体分析过程如下:
步骤1:找出关系式,矩形的面积=长×宽;
步骤2:找对应函数关系,S=l(30-l);
步骤3:确定自变量l的取值范围0 步骤4:利用配方法或者公式法求得S=l(30-l)的顶点坐标为(15,225); 步骤5:当l是15m时,场地的面积S最大. 在函数的教学过程中,需要注重函数的应用价值,从学生的实际经验出发,把实际问题抽象成数学问题,建立数学模型,寻求一题多解,发散学生数学思维.
