再谈“两边夹 夹出美丽的答案来”

甘超一

(华南农业大学资源环境学院2019级环境科学2班 510642))

可以证明冰、水混合物(假设它们之间已经没有热传递，即两者温度已经达到一致)的温度是0℃：因为冰、水混合物的温度≤冰的温度≤0℃；冰、水混合物的温度≥水的温度≥0℃，即

0℃≤冰、水混合物的温度≤0℃

①

所以冰、水混合物的温度=0℃

②

这就是文[1]介绍的一种解题方法——“两边夹(即式①)，夹出美丽的答案(即式②)来”.本文再用例题介绍这种巧妙的解题方法.

一、函数问题

题1 (2016年福建省高一数学竞赛试题第6题)f(x)是定义在R上的函数，若f(0)=1，且对于任意的x∈R，满足f(x+2)-f(x)≤2,f(x+6)-f(x)≥6，则f(2016)=( ).

A.2013 B.2015 C.2017 D.2019

解C.可得6≤f(x+6)-f(x)=[f(x+6)-f(x+4)]+[f(x+4)-f(x+2)]+[f(x+2)-f(x)]≤2+2+2=6,所以f(x+2)-f(x)=2,f(x+2)=f(x)+2.

再用数学归纳法可证得f(x+2k)=f(x)+2k(k∈N)，所以f(2016)=f(0+2016)=f(0)+2016=2017.

题2若函数cf(x)=x2+bx+c(b,c是常数)同时满足：f(1)=0；∀x∈[1,3],f(x)≤0；f(x)在(2,+∞)上是单调递增函数，则f(x)的解析式是____.

解f(x)=x2-4x+3.由f(1)=0，可得b=-c-1.

再由f(3)=9+3b+c=6-2c≤0，可得c≥3.

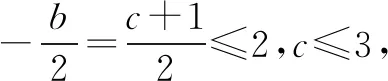
还可检验：当f(x)=x2-4x+3时，∀x∈[1,3],f(x)≤0，所以所求答案是f(x)=x2-4x+3.

(2)已知函数f(x)=ax2+bx+c,g(x)=ax+b(a,b,c均为常数).若当|x|≤1时，|f(x)|≤1恒成立且g(x)的最大值为2，则函数f(x)的解析式是____；

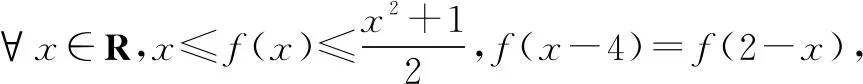
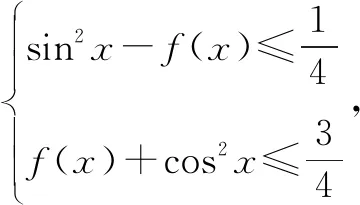
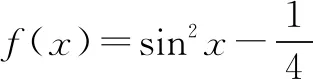
(2)f(x)=2x2-1.可得g(x)=ax+b(a>0)在x∈[-1,1]时是增函数，所以g(x)max=g(1)=a+b=2.

还可得|f(1)|=|a+b+c|=|2+c|≤1,2+c≤1,c≤-1及|f(0)|=|c|≤1,c≥-1，所以c=-1.

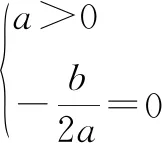
再由a+b=2，可得a=2，所以函数f(x)的解析式是f(x)=2x2-1.

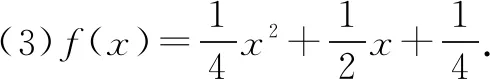
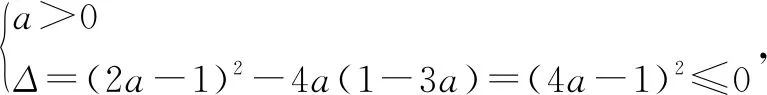
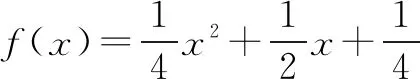
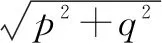
解法1 9.可得题设即∀x∈[1,5],-x2-2≤px+q≤-x2+2.如图1所示，可得线段y=px+q(1≤x≤5)夹在另两条曲线段y=-x2-2(1≤x≤5),y=-x2+2(1≤x≤5)之间.

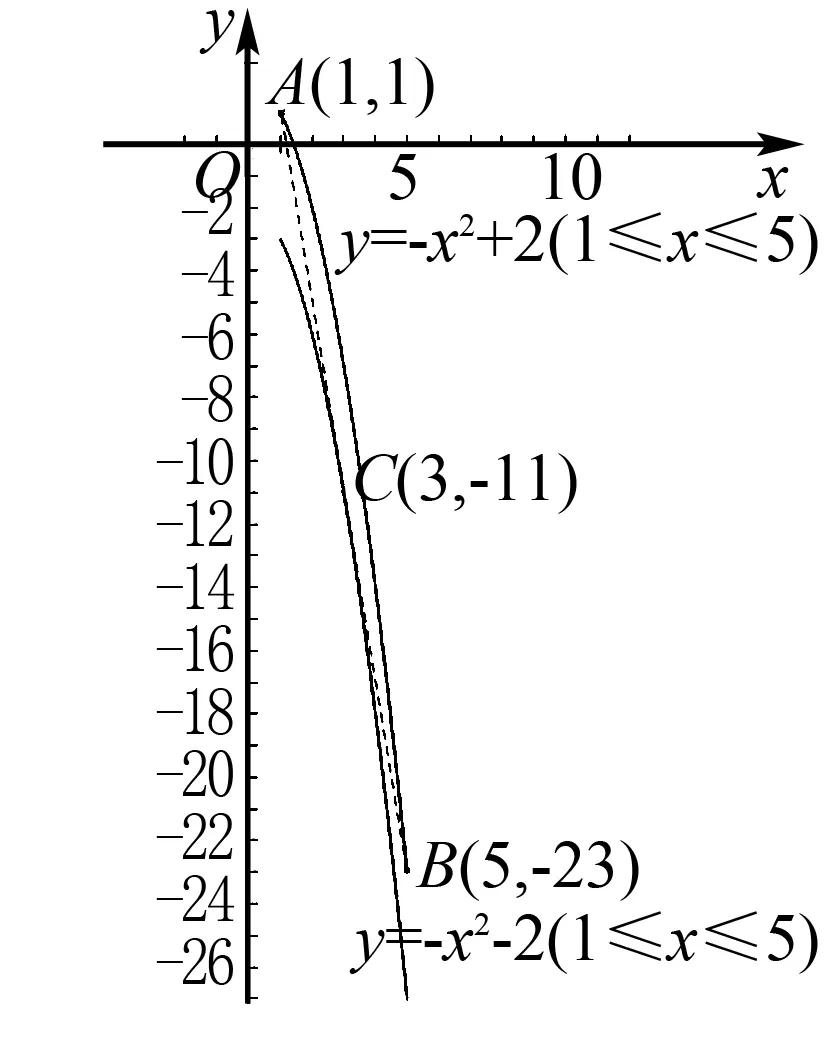
图1

可得曲线段y=-x2+2(1≤x≤5)的两个端点分别为A(1,1),B(5,-23)，还可证得线段AB:y=-6x+7(1≤x≤5)与曲线段y=-x2-2(1≤x≤5)切于点C(3,-11)，再由数形结合思想可得p,q的值分别是-6,7.

但还需要作严格证明：

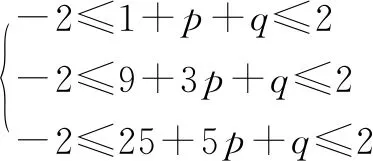
也可这样证明：

分别令x=1,3,5，可得p+q≤1,3p+q≥-11,5p+q≤-23，所以

-23≥5p+q=2(3p+q)-(p+q)

≥2·(-11)-1=-23

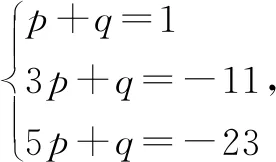
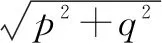
解法2 9.令x=1,3，分别得

-2≤1+p+q≤2

③

-2≤9+3p+q≤2

④

④-③，④-③×3，分别得

-6≤p≤-2,-1≤q≤7

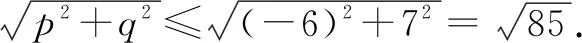
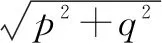
解法3 9.分别令x=1,3,5，可得

p+q≤1

⑤

-3p-q≤11

⑥

5p+q≤-23

⑦

⑤+⑥×2+⑦，得0≤0，所以⑤⑥⑦均是等式，进而可求得p=-6,q=7.

同解法2，还可验证p=-6,q=7满足题设，所以满足题设的p,q的值分别是-6,7.

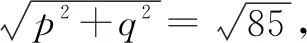
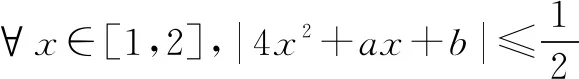
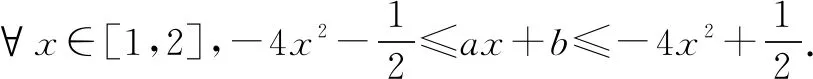
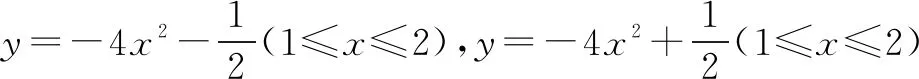
但还需要作严格证明：

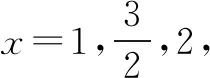
也可这样证明：

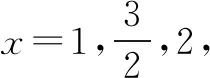
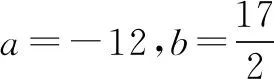
注同题4或题5的解法还可证得下面的结论：

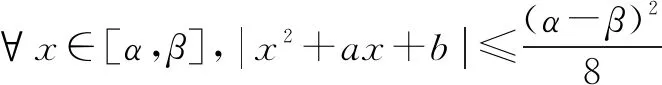
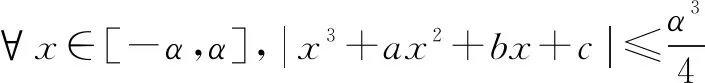
由题4或题5的解法还可解答这道小题：

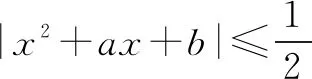
A．实数a有唯一取值 B．实数a的取值不唯一

C．实数b有唯一取值 D．实数b的取值不唯一

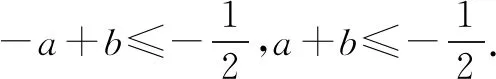
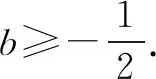
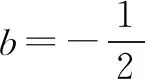
因而选项A,C均正确，B,D均错误.

二、方程问题

题6 若自然数a,b,c满足29a+30b+31c=336，则a+b+c=____.

解11.由题设，可得

29(a+b+c)≤336≤31(a+b+c)

a+b+c=11

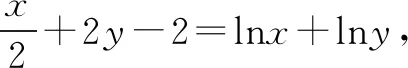
(2)若实数x,y满足x+y+4=ex+ey+2，则x+y=____.

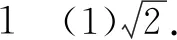
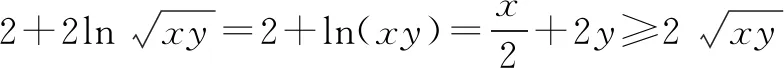
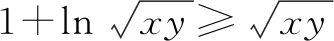
用导数可证得不等式1+lnt≤t(当且仅当t=1时取等号)，所以

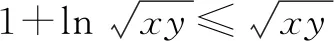
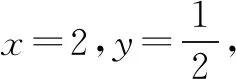
(2)-2.由题设及均值不等式，可得

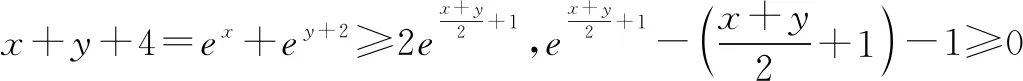
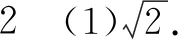
用导数知识，可证得

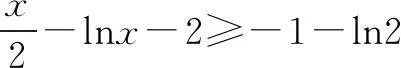
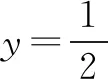
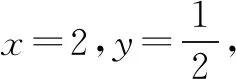
(2)-2.可得题设即x-ex+4=ey+2-y.

用导数知识，可证得

x-ex+4≤3(当且仅当x=0时取等号)

ey+2-y≥3(当且仅当y=-2时取等号)

所以题设即x=0,y=-2，因而x+y=-2.

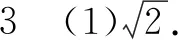
用导数知识，可证得

t-lnt-1≥0(当且仅当t=1时取等号)

所以

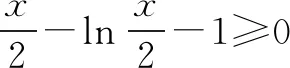
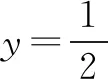
(2)-2.可得题设即(ex-x-1)+[ey+2-(y+2)-1]=0.

用导数知识，可证得

et-t-1≥0(当且仅当t=0时取等号)

所以

ex-x-1≥0(当且仅当x=0时取等号)

ey+2-(y+2)-1≥0(当且仅当y=-2时取等号)

进而可得题设即x=0,y=-2，所以x+y=-2.

三、三角函数与解三角形问题

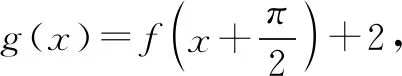
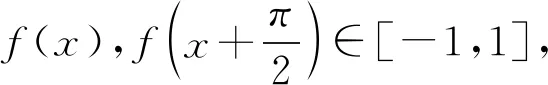
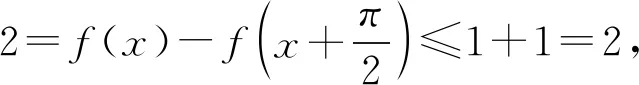
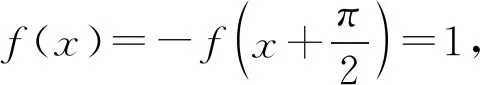
进而可得答案是C.

注用以上“两边夹”的方法还可求解2020年高考北京卷第14题：若函数f(x)=sin(x+φ)+cosx的最大值为2，则常数φ的一个取值为____．(笔者注：建议把题中的“取值”(动词)改为“值”(名词)，或把“φ的一个取值”改为“φ可取的一个值”.)

题9 在△ABC中，角A,B,C的对边分别为a,b,c.

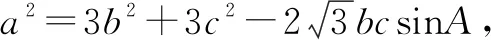
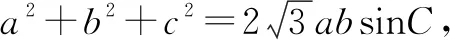
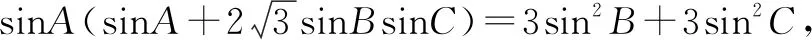
⑧

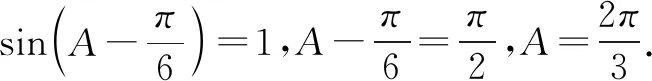
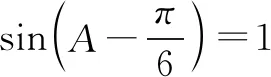
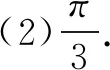
把此等式与题设中的等式相加后，可得

再由不等式a2+b2≥2ab，

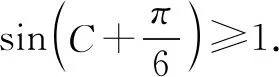
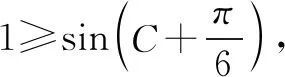
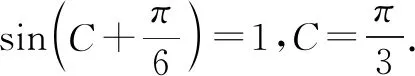
再由余弦定理，可得

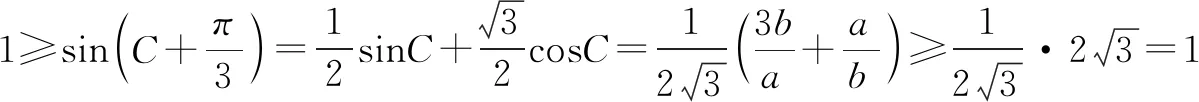
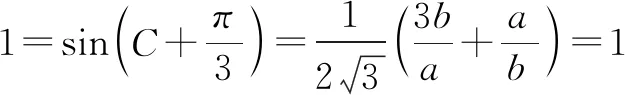
从而可得答案.

四、平面向量问题

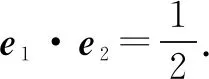
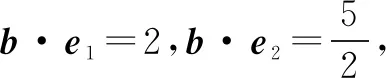
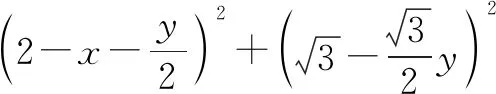
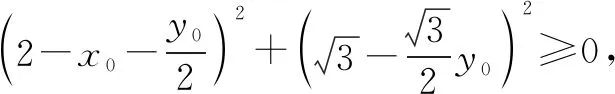
五、求取值范围问题

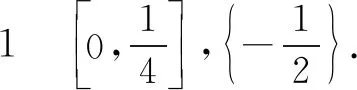
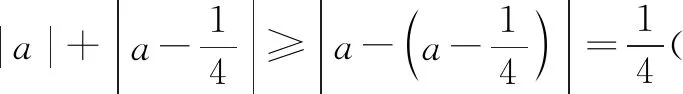
把得到的两个不等式相加，并由题设可得

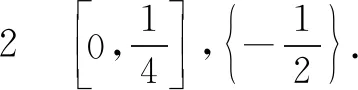
还可得

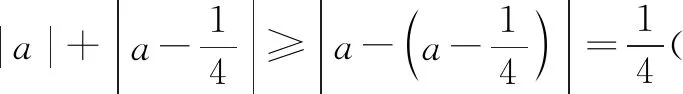
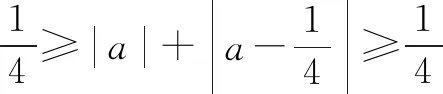
进而可得答案.

六、恒成立问题

题12 (2012年高考浙江卷理科第17题)设a∈R，若x>0时均有[(a-1)x-1](x2-ax-1)≥0，则a=____.

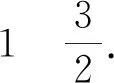
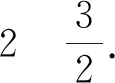
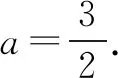
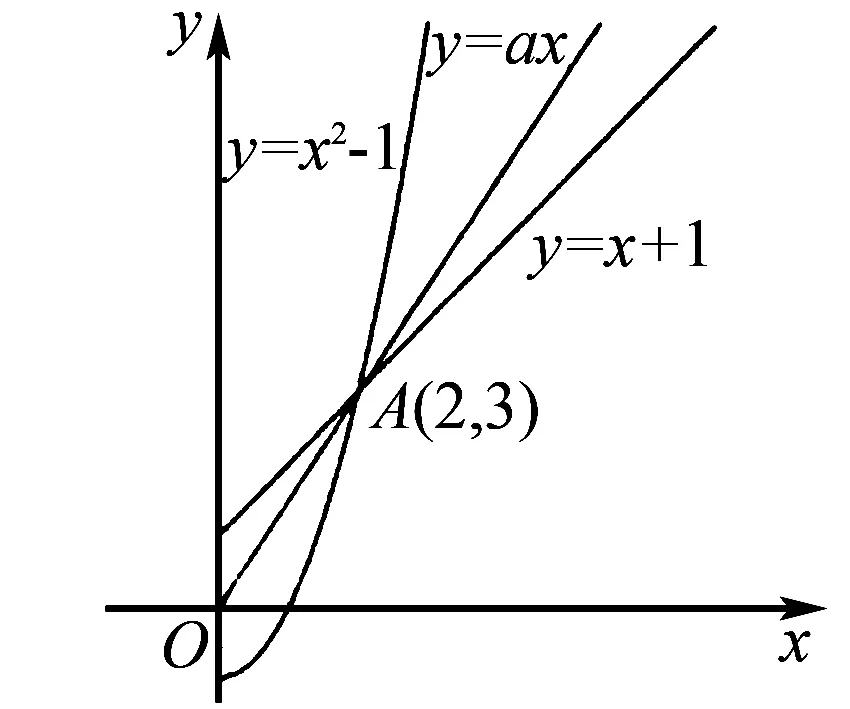
图2

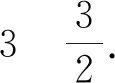
注在解法3中，为什么会想到令x=2呢？

题13(1)若x∈[-1,1]时，ax3-3x+1≥0恒成立，求实数a的取值范围；

(2)若x∈[-1,1]时，f(x)=ax5-20x3+5x-1≤0恒成立，求实数a的取值范围；

(3)若x∈[-1,1]时，f(x)=ax5-20x3+5x+1≥0恒成立，求实数a的取值范围．

解(1)可设x=sinα，由公式sin3α=3sinα-4sin3α，得(4-α)sin3α≤1-sin3α恒成立．

还可验证当a=4时(4-a)sin3α≤1-sin3α恒成立，所以所求答案是“4”．

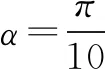
还可验证当a=16时(a-16)sin5α≤1-sin5α恒成立，所以所求答案是“16”.

(3)在(2)的结论中，令x=-t后可得答案是“16”.

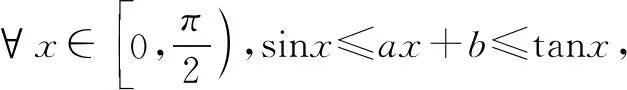
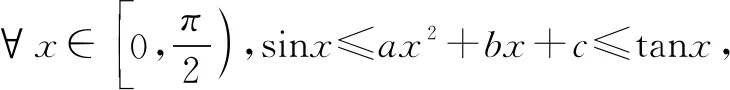
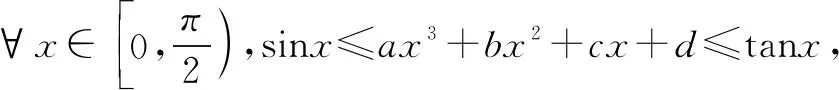
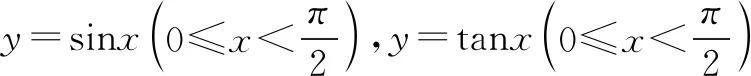
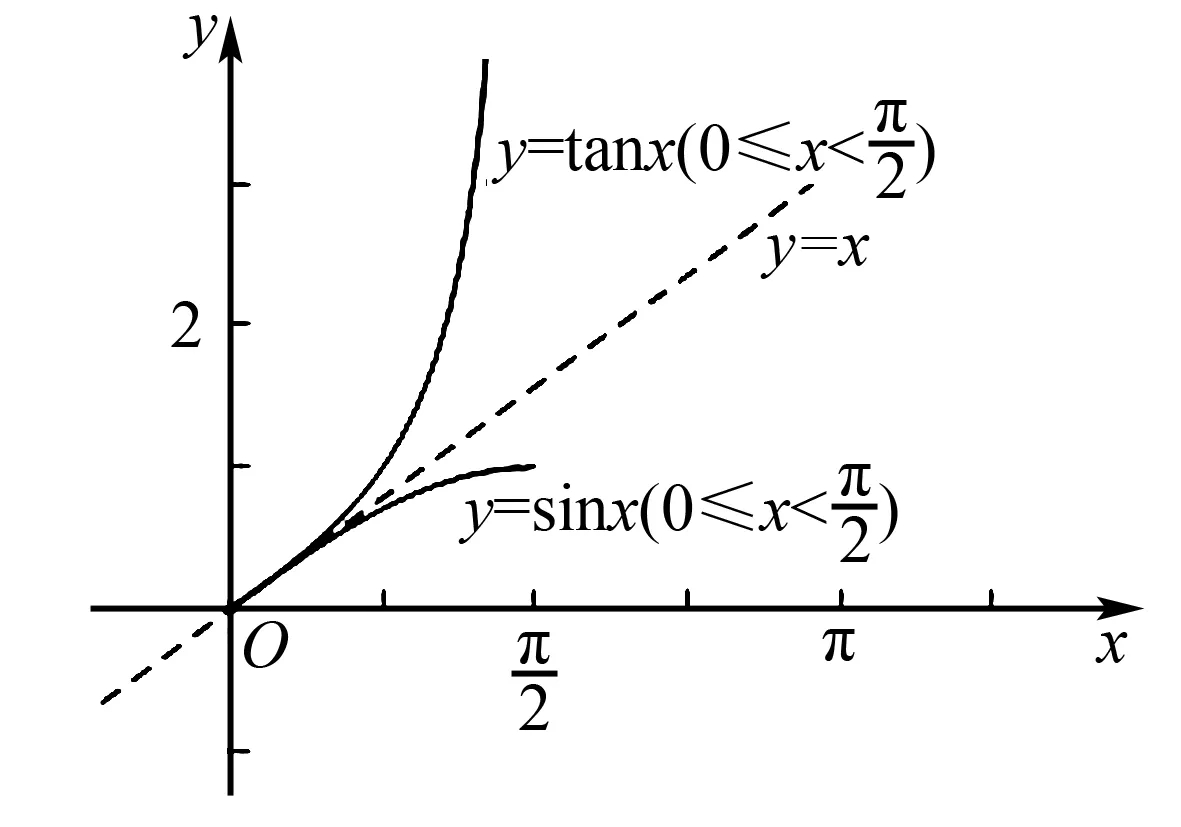
图3

但以下解答更严谨：

在sinx≤ax+b≤tanx中令x=0，可得b=0.

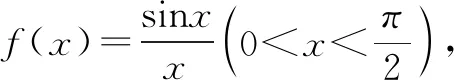
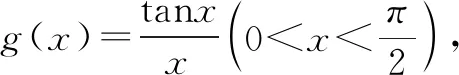
所以a=1.得所求常数a,b的取值范围分别是{1},{0}.

(2)同(1)的解答可得c=0.

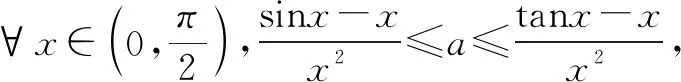
⑨

所以a=0.得所求常数a,b,c的取值范围分别是{0},{1},{0}.

(3)同(2)的解答可得d=0,c=1.

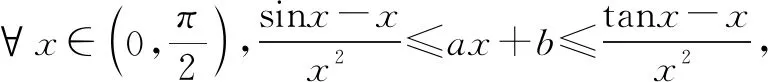
再由⑨，可得b=0.

注有兴趣的读者，还可研究题15的一般情形.

七、其他问题

文献[1]的题1(第 54 届罗马尼亚数学奥林匹克决赛试题)，题2(2008年北京市中学生数学竞赛高一年级初赛试题第一题第4题)，题10(2007年全国高中生数学联赛江苏赛区初赛试卷第15题)及题13(2012年卓越联盟自主招生数学试题第12题)，题11(2012年第24届亚太地区数学奥林匹克竞赛第1题)，题14用“两边夹”分别解决了求值问题、存在性问题、数列问题、平面几何问题、求极限问题，读者可自行浏览.