减小解析几何运算量的一个重要策略——恰当选择直线方程

李昌成 向 前

(1.新疆乌鲁木齐市第八中学 830002；2.新疆乌鲁木齐市第64中学 830063)

高考试题中很多解析几何综合题目都是在直线与圆锥曲线相交的条件下命制出来的，这些题目经常作为小题的把关题，大题的压轴题，考查学生的综合能力.学生普遍对此有几分畏惧.究其原因，在解题入口处就埋下了隐患——直线方程形式选择不一定恰当，导致后续解答形式复杂，过程冗长，函数关系不明晰，最终问题搁浅.高中阶段课本共介绍了6种形式的直线方程，在解答圆锥曲线问题时，学生习惯使用斜截式y=kx+b和点斜式y-y1=k(x-x1).实际上，这是不合适的，应该根据已知条件和所求问题选用不同的形式，达到优化过程，减少运算，提高准确率的目的.下面以高考题为例，说明如何选择直线方程，形成最佳解法，以飨读者.

一、 典型案例

例1(2017年全国高考数学理科Ⅰ卷第10题) 已知F为抛物线C:y2=4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为( ).

A.16 B.14 C.12 D.10

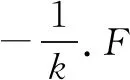
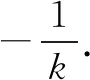
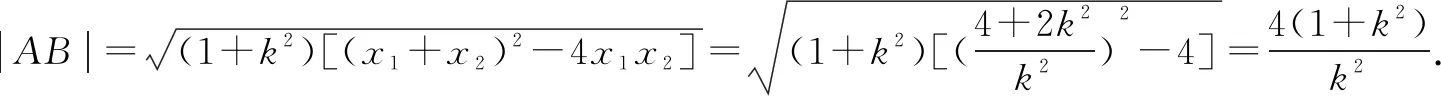
评注本解法是学生最容易想到的，但实际上是最麻烦的.首先，要考虑直线斜率的存在性，若遗忘可能造成最值不存在(很多题的最值就出现在斜率不存在的特殊情形处).其次，这种直线方程对应的弦长公式最复杂，给后续运算带来隐患，增加了答案的不确定性.再次，函数模型比较繁杂，往往需要多次构造，等价转化为利用均值不等式或对勾函数求最值问题，学生一般掌握得不太好，堵住了出口，致使整个解答搁浅，前功尽弃！

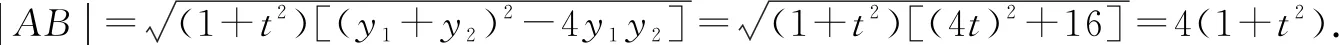
评注直线的这种表示方式教材上并没有给出，而是一线老师在教学实践中实践总结出来的.通过本例我们可以感受到用它解题相对于解法1要简单一些，无论是求弦长，还是构造函数，还是求函数的最值，它都显得简洁明了.

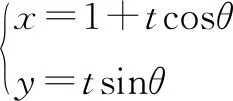
由已知得，直线AB与直线DE垂直，则直线DE的倾斜角为90°+θ，则

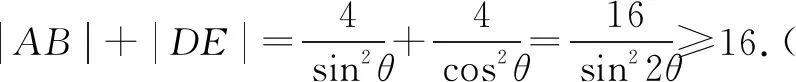
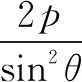
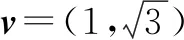
(1)求椭圆C的方程；

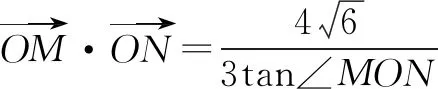
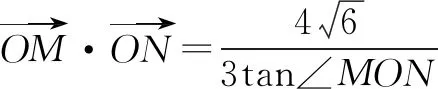
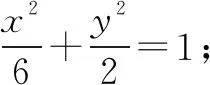
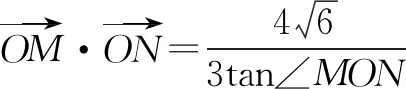
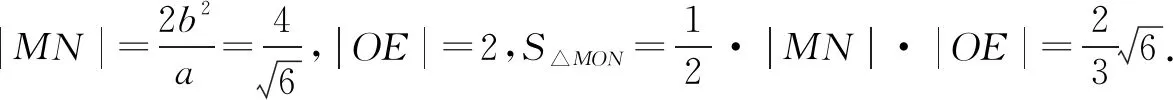
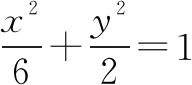
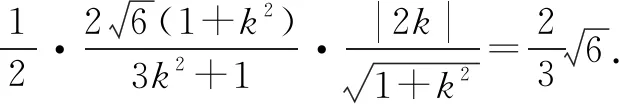
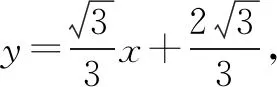
分析2 本题的实质是已知ΔMON面积的情况下，求直线方程.注意到线段OE是定值，我们可以将ΔMON分成ΔMOE和ΔNOE，两个三角形的面积分别可以被点M，N的纵坐标表示，因此可以设m:x=ty-2，避开讨论作答.

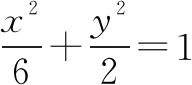
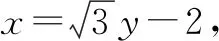
评注对比以上两种解法可以看出，解法1从点斜式直线入手，分类讨论，思路简单，过程冗长，计算繁杂；解法2从x=ty+a的直线形式入手，有效避开讨论，充分利用常数，运算简捷，答案形式也爽心悦目，解法不失一般性，明显优于解法1.

二、探究规律

在解直线和圆锥曲线的综合题时，我们一定会面临直线形式选择问题.哪一种最好，要因题而异，不可一概而论.一般地，当已知直线的斜率时，首选斜截式或参数方程；当已知直线过定点时，有三种情形：定点为(0,b)(b为直线的纵截距)首选斜截式；定点为(a,0)(a为直线的横截距)首选x=ty+a或参数方程；定点为(m,n)首选点斜式或参数方程；曲线类型也对直线选择影响较大；问题等价转化形式对直线选择影响更大.因此，直线方程形式的选择实际上是一个瞻前顾后的工作，是一个统领的工作，我们要在实践中积累经验，作为一种技能来掌握它，提高应对解析几何的综合能力.

三、 应用实践

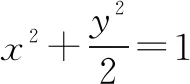
提示本题的关键是求弦长，而两弦共已知点且垂直，于是两直线的倾斜角相差90°，因此最好选择直线参数方程解题，将问题归结为求三角函数的最值.

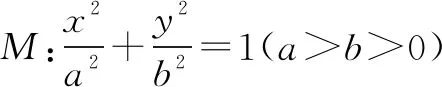
(1)求M的方程；

(2)C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

提示对于(2)，直线AB的斜率为-1，因为CD⊥AB，所以直线CD的斜率也就是1，所以直线CD用斜截式y=x+t表示，易于用t表示|CD|.四边形ACBD面积由|AB|，|CD|决定，|AB|是常数，所以四边形ACBD面积S就被表示成关于t的函数，易求得其最大值.

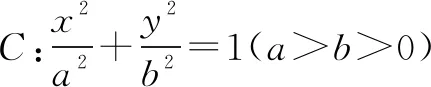
(1)求椭圆C的标准方程；

(2)过椭圆C右焦点F2的直线l与椭圆C交于不同的两点A，B，求△F1AB的内切圆的半径的最大值．

提示对于(2)，设A(x1，y2)，B(x2，y2)，设△F1AB的内切圆的半径为R，利用内切圆的性质得，△F1AB的周长和R可以表示其面积.另外，注意到|F1F2|是定值，所以△F1AB面积又可以用|y1-y2|表达，所以设直线l的方程为x=ty+c(由第一问知c=1)，通过等面积法建立R与t的函数关系，求得内切圆半径的最大值．

通过前瞻性的选择直线方程能够从宏观上把控解析几何的解题思路.加强思考总结，有助于准确把握问题的内涵，找到突破途径，克服畏惧心理，全面提高学生的解题能力.