数形结合思想在高中数学解题中的应用

景 艾

(甘肃省景泰县第二中学 730400)

数形结合不仅是一种数学思想，而且还是种解题方法，并能够促进学生抽象与形象的思维实现有效结合.因此，在高中数学的解题中，数形结合思想的运用，不仅可以使抽象化数学语言通过更形象、直观的形式呈现出来，而且能够把数字与图形实现完美结合，并以促进学生自身解题效率的提高.通过数形结合思想的运用，不仅能促进数字与图形的有效转换，而且还能把复杂的数学问题转变的更加简单，从而确保数学试题严谨性的同时，实现解题流程以及方式的优化.基于此，本文主要对高中数学解题中数形结合的运用原则进行分析，并提出数形结合在数学解题中的应用策略.

一、数形结合在高中数学中的应用原则

在面对相关数学问题的时候，学生完成数学题干的分析后，可以将相关数学知识转变为图形.因此，数学问题的解决时，教师需注重数形结合的思想渗透，促进图形与数量关系的有效整合，从而确保学生实现高效解题.在高中数学的解题中应用数形结合的思想，需注重下述原则的遵循：

首先，等价性原则.数形结合的运用，最重要的就是把握等价性原则，该原则主要指题目当中的条件与关系，若通过外形呈现，通常不会有任何的背离与偏差.数学能够使人精细，主要是因为数学知识能够对学生的观察力、分析力、应用能力实施考验与提升.若学生在赋予形的过程当中，扩大题目给出的定义域、值域以及对应法则等相关条件，就会出现离题千里的现象，因此，需注重数形之间的等价原则.

其次，双向性原则.数形结合的运用，需牢记“以形助学，以数解形”.通常来说，就是学生需注意两条腿走路，若只是单方面的运行与努力，在解题时，就容易误入歧途.对于数学题目而言，其通常较为复杂且综合，这就需学生通过图形与运算促进题目的解决.

再次，简单性原则.数形结合运用的本质就是使数学题目变得更简单，如果数形结合的运用没有使数学题更加简单且更复杂，那就是学生自己解题产生了问题，如方程求解中出现了问题，或者图形展示出现了问题，主要是因为运用数形结合的目的是解决问题，不是制造新问题.

最后，实用性原则.数形结合的运用目的主要是为了解题，而非为了对数形结合进行应用，因此，学生在运用中，需注重实用性原则，只有满足实践需要，才能应用数形结合.因此，在较为简单的数学题解答时，并非一定要运用数形结合，而需将其运用于复杂数学题的解答上.

二、数形结合在高中数学解题中的应用策略

1.基于数形价值的解题意识发展

数形结合通常能够使复杂且抽象的数量关系实现形象直观的呈现，因此，数学教师在解题的教学中，需注重数形结合的思想渗透，关注学生的解题意识以及思维能力的有效培养，以促使学生能够在观察、抽象、归纳、概括、分析过程中，突破原先的数学思维，经过数和形的有效转化与归纳，并对新的解题方法与思路进行探索，以促使学生通过分析与解题，深刻体会到数与形有效结合的解题价值与优势，从而使学生形成数形结合的良好解题意识.

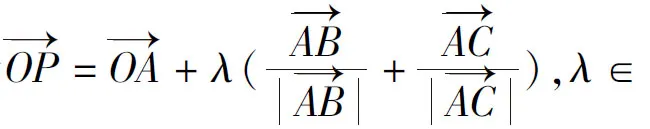
通过数形结合进行问题解决时,数学教师需注重构图的合理性与准确性.通过几何图形激发学生自身的直观思维,并引导学生通过图形的意义、性质与优势,实施严谨化计算与分析,从而使学生能够依据数学题目,在图形当中找出相应的解题思路,如图1所示.

2.基于数形结合的解题思路拓展

高中数学的解题当中融入数形结合的思想，想要确保数和形的互相渗透，并使学生能够通过探索分析，由整体的结构构建出抽象概念和具体形象之间的联系，经过数和形的互相表征，实现学生的解题思路开拓.因为数形结合的问题解决过程中，涉及到数和形的有效转化，数学教师在学生解决习题的时候，就需通过图形具备的性质，加强学生的创造性思维培养，并指导学生从各个角度、多个层面进行问题思考与分析，并通过题意的结合，立足于数形两个方面实施表征，并找到问题突破口，从而使学生充分体会到新知识的探索兴趣.数学教师可引导学生探寻数形之间的转化，指导学生在相同的坐标当中画出相应的函数图象，以此对图形的意义与性质进行直观挖掘，引导学生根据数联想出形，通过加强学生对于知识的理解，增强学生对于数形转变的经验，并指导学生合理巧妙的运用数形结合的思想，从而为学生创造良好的学习条件.

例如，假设直线x=t和函数f(x)=x2与g(x)=Inx的图象相交于点M、N，当|MN|取最小数值的时候，求取t值.

数学教师可引导学生依据题意探究出数形之间的转化途径，在相同的坐标系当中画出相应的函数图像，如图2，引导学生经过独立自主探寻出相应的思考过程，并对数和形进行有意识转化，充分发挥解题新思路.

3.基于数形结合的解题能力强化

高中数学的解题过程中融入数形结合的解题思想，关注学生的批评、探究、反思各项能力的培养，引导学生在解题中，对数学语言实施细致的观察，并经过全面、周到的自主构图实施严谨且准确的思考与分析，并经过数形结合的思想，获得准确结论.基于此，想要使学生运用数形结合的解题思想得到有效强化，数学教师可引导学生对常规的解题思路与数形结合的解题思路相对比，引导学生通过观察、对比、归纳，深刻的理解到数形结合具备的优势，以促使学生自身的解题意识以及能力得到有效提高.

在学生实施推理与构图的时候，数学教师需通过循序渐进的原则，引导学生通过图形揭示出数学知识的概念，并经过从感性至理性的认知，对数形结合实施巧妙应用，从而使学生充分掌握相关数学知识.如图3所示：

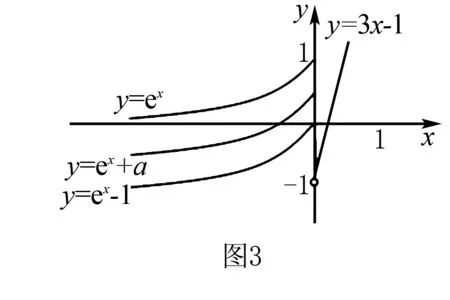
当x>0的时候，f(x)=3x-1存有一个零点时，x=1/3，所以，当x≤0时，f(x)=ex+a=0存有一个实根.根据图形结合可得，-1≤a<0.从而使学生在数学题解题中，交叉且灵活的渗透形象和抽象化思维，从而使学生自身的数学解题力得到显著提高.

综上所述，在高中数学的课堂解题教学中，数形结合的思想运用，其不仅能够使数学学科的教学效率与质量得到有效提高，而且还能促使学生充分掌握该高效化的解题方式，并经过直观方式将数学题目呈现给学生，以此使学生通过该方式，对复杂化的数学问题实施分析，并抓住问题的关键点，促使学生实现高效化解题，并使学生自身的解题能力得到显著提高.