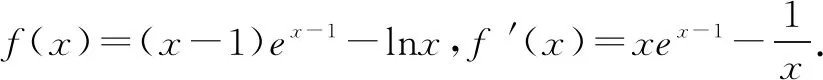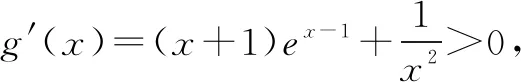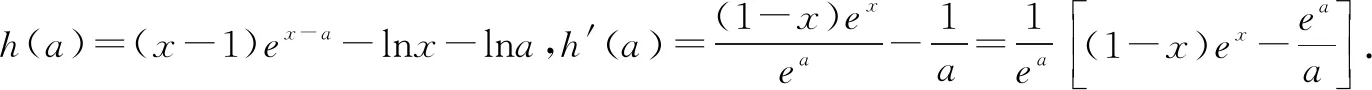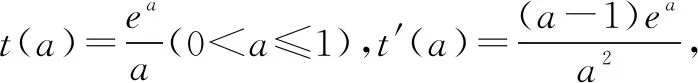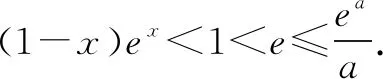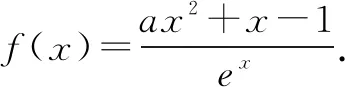主元法证明含参不等式
2021-08-05杨苍洲庄津津
杨苍洲 庄津津
(1.福建省泉州第五中学 362000;2.福建省南安五星中学 362000)
利用导数证明含参数不等式的试题中,经常涉及到多个变量(如含有变量a,x两个变量).受惯性思维的影响,解题者往往会选择以x为主元进行求解.以x为主元进行求解的解题过程经常是比较繁琐的,此时,我们不仿改变一下角度,先选择变量a为主元,把问题视为关于变量a的不等式,并加以解决,从而消去变量a;消去变量a后的等式只含有变量x,我们自然地选择以变量x为主元,再构造关于x的不等式进行证明.这样的证明过程,会使得解题过程显得格外简捷自然.
例题1(武汉市2021届高中毕业生三月质量检测)已知函数f(x)=(x-1)ex-a-lnx.
(1)当a=1时,求f(x)的最小值;
(2)证明:当0 又f′(1)=0, 故当0 当x>1时,f′(x)>0,f(x)单调递增. 故f(x)在x=1处取得最小值f(1)=0. 设s(x)=(1-x)ex(x>0),s′(x)=-xex<0,所以s(x)在(0,+∞)单调递减,s(x) 即h′(a)<0,h(a)在(0,1]单调递减. 故h(a)≥h(1)=(x-1)ex-1-lnx. 由(1)知,(x-1)ex-1-lnx≥0. 故0 在上述问题(2)中,如果以x为主元求解较为繁琐.此时重新确定a为主元,要证f(x)≥lna,只要证h(a)≥0(0 例题2 (2018年高考新课标1卷文科)已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点.求a,并求f(x)的单调区间; 解析(1)略. 当0 当x>1时,g′(x)>0. 所以x=1是g(x)的最小值点. 故当x>0时,g(x)≥g(1)=0. 所以h(a)≥0. (1)求曲线y=f(x)在点(0,-1)处的切线方程; (2)证明:当a≥1时,f(x)+e≥0. 解析(1)略. 令g(x)=x2+x-1+ex+1,则g′(x)=2x+1+ex+1,g″(x)=2+ex+1>0,所以g′(x)在R上单调递增,又g′(-1)=0,故当x<-1时,g′(x)<0;当x>-1时,g′(x)>0,所以x=-1是g(x)的最小值点. 故g(x)≥g(-1)=0. 所以当a≥1,h(a)≥g(x)e-x≥0,即f(x)+e≥0. 在上述问题(2)中,要证f(x)+e≥0,只要证h(a)≥0,即证h(a)min≥0.利用h(a)在[1,+∞)的单调性,得到h(a)最小值h(1),最后证h(1)≥0.将复杂的问题转化为简单的问题,提高解题效率. 例题4 (2013年高考新课标2卷理科)已知函数f(x)=ex-ln(x+m). (1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性; (2)当m≤2时,证明f(x)>0. 解析(1)略. (2)(定主元m)设h(m)=ex-ln(x+m)(x≥-m), 所以h(m)≥h(2),即h(m)≥ex-ln(x+2). 又g′(-1)<0,g′(0)>0. 故g′(x)=0在(-2,+∞)有唯一实根x0,且x0∈(-1,0). 当x∈(-2,x0)时,g′(x)<0;当x∈(x0,+∞)时,g′(x)>0. 所以x=x0是g(x)的最小值点. 所以h(m)≥g(x)>0. 综上所述,当m≤2时,f(x)>0. 在上述问题(2)中,对于已知参数m取值范围,证明不等式成立,可以先把m视为主元,因此要证f(x)>0,只要证h(m)>0,即证h(m)min>0.利用h(m)在m∈(-2,+∞)的单调性得到最小值h(2),最后证h(2)>0.整个解题过程自然流畅,思路清晰,十分简捷.