基于构造法的高中数学解题方法探讨

段黾钊

(江苏省南通市海门市包场高级中学 226100)

数学知识具有比较强的繁杂性与抽象性特性，是高中生学习的重点与难点所在，尤其是其中涉及到许多复杂性与综合性比较强的类型题，常常使学生陷入解题困境.在正向解题思路下无法快速求解数学问题，如果可以灵活地应用逆向思维，借助构造法分析问题，那么就可以通过对题干中的隐性及显性解题信息进行挖掘来快速明确求解问题所必备的关键解题条件与信息，进而可以简化学生求解问题的过程，提高了他们求解数学问题的能力.

一、基于构造方程法，求解数学问题

构造方程法是求解高中数学题中用的比较多一种解题方法，主要是由于方程和函数之间具有紧密联系，许多数学类型题常常都可以通过寻求方程和函数之间的相关性来进行求解.构造方程法主要是在对相关问题中的已知条件以及它们之间的相关性进行深入分析的基础上，通过利用这些已知关系与条件来相应地构造能够求解问题的等量方程.

例1已知(m-n)2-4(n-x)(x-m)=0，试求参数m，n，x之间互相构成等差数列.

解析在求解这道与数列相关的类型题中，如果采用传统求解方法，那么整体的求解难度比较大，并且还会使学生进行大量的计算，容易造成错解情况.此时在求解这道问题中可以灵活地运用构造法，以“参数m，n，x之间互相构成等差数列”这一待求解条件作为求解问题的已知条件，同(m-n)2-4(n-x)(x-m)=0这一给定的关系式相结合，那么可以具象化和简单化处理这道抽象数学问题，大大提高了问题求解效率.

解构造如下方程：(m-n)t2-(m-n)t+(x-m)=0；

令F(t)=(n-x)t2+(m-n)t+(x-m).

通过分析本道题，可以发现：F(1)=0，可知：(n-x)t2+(m-n)t+(x-m)=0的实数根保持相等，求解可得：t=1，所以可知相应方程实数根均为1.然后可以结合韦达定理来得到如下方程：m+n=2x，所以可知参数m，n，x之间互相构成等差数列.

基于上述分析可知，在求解这道问题中，核心解题思想是借助构造法的运用来简化复杂的问题，提高问题求解的准确率与效率.

试求：tan(α+β+γ)的值.

解析针对上述这道涉及到三角函数的问题，学生在求解的过程中如果直接采取分解待求函数tan(α+β+γ)的方式来求解问题，那么会大大增加学生求解问题的难度，并且非常容易出现错解情况.此时如果灵活应用构造方程的方法来简化问题，那么可以大大提高解题的便捷性与准确度，并且可以避免因为计算量过大而造成错解情况的出现.

解假定tanα=x，tanβ=y，tanγ=z,那么基于给定的题干条件可知，

由此可见，灵活运用构造方程思想等一些方法来简化问题求解过程，这样可以最大程度提高学生求解数学问题的质量与效率.

二、基于构造数列法，求解数学问题

数列作为高中数学教学的重要内容，是高考数学试卷必考的题目.其中主要涵盖了等差数列、等比数列两个方面的数列知识，但是却依旧包含比较多的数学内容.在求解数列问题时，如果可以灵活地运用构造数列的方法，那么在求解部分数学题目中常常会发挥非常神奇的效用，具体就是借助联想或替换等方法来构建等比数列或等差数列，之后结合数列方面的相关知识来深入分析题干当中的相关信息、条件及要求，这样可以极大地简化问题，提高问题分析及解决的有效性.

解析基于题干信息，给出部分解题条件与信息来求解Sn是一道比较常见的类型题.在明确前几项之和，且给定了{an}这一通项公式，所以可以借此来推算出相应的Sn表达式.

解基于问题题干信息可得，在n≥2的时候，an=Sn-Sn+1，所以可知：

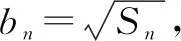
三、基于构造函数法，求解数学问题

同构造方法这一解题方法类似，构造函数法也是求解数学问题中比较常见的一类解题方法，二者本质在解题上存在相通性.在平时的解题教学中，可以结合具体的解题来指导学生同时训练自身灵活应用构造函数法求解数学问题的能力.通过有效应用构造函数法分析及求解数学问题，可以锻炼学生思维的灵活性，尤其是在代数问题、三角函数问题、几何问题等相关数学类型题当中.如果可以指导学生深入挖掘所给数学题目中的关键信息，找到其中有关的函数关系，那么可以将这些复杂数学问题的求解过程进行简化，配合函数问题求解方法及思想的灵活应用可以大大提高学生求解数学问题的能力，同时借助构造函数方法的灵活应用可以进一步提高整体的解题准确率.

例4已知a,b,c,d均为实数，且满足：针对任意一个实数x，均满足下一不等式：acosx+bcos2x+ccos3x+dcos4x≤1.试求：a+b-c+d的最大值，以及此时a,b,c,d各自的值是多少？

解析在求解这一道三角函数相关的类型题中，由于其中涉及到a,b,c,d几个未知参数，所以在对相应不等式进行化简的时候会遇到一些难题，学生常常不知道该如何解题.此时如果可以灵活应用构造函数法，那么可以将复杂的三角函数问题进行简化，快速找到解题的突破口，避免大量的计算.

解令f(x)=acosx+bcos2x+ccos3x+dcos4x

此时可以令t=cosx(-1≤t≤1)，那么可知:

f(x)-1=acosx+bcos2x+ccos3x+dcos4x-1

通过进一步简化上式，可以得到：

f(x)-1=2(t-1)(t+1)(2t-1)[2dt-(1-d)]≤0

针对定义域为(-1≤t≤1)范围内的t，上式均成立，所以可知：d>0，且2d/2=(1-d)/1，求解得：d=1/2.这样可以快速求解本道题的正确答案为：最大值为3，且对应最大值时候a，b，c，d分别为1，1/2，-1和1/2.

综上所述，在求解某些数学问题中，如果可以指导学生巧用构造法，通过构造数列、构造函数以及构造方程，可以有效简化求解的问题，大大提高学生解题的准确度与效率.但是在实际求解问题中应用构造法期间，必须要结合实际的类型题进行合理分析，保证可以选择适宜的构造法来简化问题，这样才能不断提升学生运用构造法解题的能力.