如何依据前摄抑制和后摄抑制理论提升学生数学解题能力

龚 飞

(江苏省南通市启东市第一中学 226200)

前摄抑制和后摄抑制理论，是指学生前后所学知识之间相互影响，导致学生容易遗忘知识.在前摄抑制和后摄抑制理论的背景下，教师应当有效地帮助学生了解前后所学知识的联系与区别，从而更好地基于已有知识，掌握新的知识.具体在高中数学解题教学领域，教师应当基于学生当前解题学习内容，巧妙设置校本例题，促进学生能够在已有知识基础上，有效掌握新的知识与新的解题方法，充分调动学生的学习积极性与学习能力，帮助学生获得高质量的解题学习效果.以下结合具体高中数学解题教学情况，进行详细分析.

一、前摄抑制和后摄抑制理论对于高中数学解题教学的影响研究

高中数学的知识体系与小学数学、初中数学的知识体系有着千丝万缕的联系.虽然学生的数学知识发展是一脉相承的，但是由于学生受到前摄抑制和后摄抑制的影响，容易将各种类似数学知识混淆，从而影响学习效率，加快遗忘速度.

具体就高中数学解题教学而言，学生在小学、初中数学学习过程中形成的数学解题思维，会对他们的高中数学解题学习形成一定的干扰，即前摄抑制.同时，学生在高中数学解题教学中养成的解题习惯，也会使他们加速遗忘小学、初中数学的基本数学知识，即后摄抑制.因此，高中数学教师有必要对前摄抑制和后摄抑制理论引起重视，帮助学生理清各种数学知识之间的内在联系与外在区别，从而更好地提升学生的解题能力以及数学学习能力.

二、利用前摄抑制和后摄抑制理论帮助学生消除新旧知识之间的干扰

高中数学知识与初中、小学数学知识具有很大的联系，但是高中学生在理解类似知识的过程中，还是会出现相应的混淆，从而干扰学生的数学解题能力发展.为了帮助学生消除新旧知识之间的干扰，我们基于前摄抑制和后摄抑制理论，帮助学生有效地区分了高中数学与初中数学、小学数学知识间的区别，促使学生能够准确理解各阶段数学知识，并在具体的解题学习过程中，有效提升了解题能力.

例如，在苏教版高中数学必修2《空间几何体的表面积和体积》一课的教学过程中，我们基于前摄抑制和后摄抑制理论，结合学生对于小学及初中数学中几何“表面积和体积”知识的理解，在为学生明确前后知识的区别与联系基础上，设置了如下例题.

例1“如图1所示，在正三棱锥A-BCD中，E为BD的中点，F为CD的中点，G为BC的中点；H为EG的中点，I为EF的中点，J为FG的中点.已知三棱锥A-HIJ的体积为1cm3，求三棱锥A-BCD的体积.”

图1

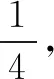
首先肯定了学生A的解答，并表示学生A通过这样的自主解题过程，有效地将小学的正三角形知识与高中的正三棱锥知识相互联系区分，在避免同类知识相互干扰的基础上，正确地解答了问题.

三、运用前摄抑制和后摄抑制理论促进学生正确区别类似知识

在小学、初中数学的知识体系中，有很多数学知识与高中数学知识十分类似，根据前摄抑制和后摄抑制理论，学生往往会对这些类似知识混淆，并且在相互影响的过程中加速遗忘.为了帮助学生有效避免受到前摄抑制和后摄抑制的影响，在高中数学解题教学中，引导学生正确区别类似数学知识，从而促使学生能够更为准确地解答高中数学问题.

例如，在苏教版高中数学必修3《随机事件及其概率》一课的教学过程中，根据前摄抑制和后摄抑制理论，结合学生对于小学及初中数学“可能性”知识的理解，设置了如下例题.

例2“将三个蓝球与两个红球放入暗箱中，每次摸取一个球，摸完放回.计算摸球三次全部为蓝球以及红球的概率.”

在学生解答这道问题之前，先向学生表示这道问题是概率论中经典的“摸球问题”，并为学生分析了小学、初中的“可能性”相关知识，只是对于概率的一种模糊描述，引导学生根据高中概率知识，准确计算出相关概率.

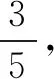
学生B的解答正确，根据对于小学、初中数学涉及的“可能性”知识的分析，为学生们明确了“可能性”只是一种模糊的概念，没有精准的值，而概率是确定的，其范围在0-1之间.从而帮助学生正确地区分了“可能性”与概率的区别，避免了前摄抑制和后摄抑制影响.

四、引导学生根据之前已掌握的数学知识生成新的数学知识

前摄抑制和后摄抑制是学生因前后知识的互相影响而加速遗忘的现象，而根据前摄抑制和后摄抑制理论，进行了相反的应用，引导学生根据小学、初中已掌握的数学知识，生成高中数学知识，从而有效地提升了学生的数学学习效率.

例如,在苏教版高中数学必修5《等差数列》一课的教学过程中，通过前摄抑制和后摄抑制理论的反向应用，结合学生对于小学及初中数学“平均数”知识的理解，设置了如下例题：

例3“在等差数列{an}中，S16-S13=27，求a15.”

学生在解答这道例题时，因为题目没有给出a1及公差d的条件，往往感觉无从下手.此时为学生分析，S16-S13，实际就是a14+a15+a16，因为{an}为等差数列，所以a14，a15，a16为等差数列连续三项，a14，a15，a16的平均数则是a15，则a15=27÷3=9.为了让学生更为清楚地了解这样的知识生成过程，特别为学生进行了a14，a15，a16的平均数是a15的证明.首先，“a14=a1+(14-1)d；a15=a1+(15-1)d；a16=a1+(16-1)d.设中位数a15为x，则a14，a15，a16分别为x-d；x；x+d；可知a14+a15+a16=3x.将a14+a15+a16=27带入方程，则3x=27；x=9.”

通过这样的方向利用前摄抑制和后摄抑制理论的教学过程，能够帮助高中学生有效地通过将小学、初中所学数学知识进行归纳，从而生成高中的数学知识，为学生构建起了巩固的数学学习基础.

总而言之，利用前摄抑制和后摄抑制理论，能够在有效帮助学生消除新旧知识之间的干扰的基础上，促进学生正确区别类似知识，并且还能够引导学生根据之前已掌握的知识生成新的知识.在高中数学解题教学的过程中，积极发挥前摄抑制和后摄抑制理论的教学实践作用，帮助学生有效分清新旧数学知识的联系与区别，并且在解题教学的巧妙引导过程中，培养高中学生具备了出色的自主解题能力，从而取得了高质量的教学成效.在今后的高中数学教学工作中，将继续研究前摄抑制和后摄抑制理论与高中数学教学的融合，在更好地提升教学质量基础上，为学生带来更多的学习裨益.