探索圆锥曲线中的存在性问题

韩 俊

(江苏省溧阳中学 213300)

探索性问题一直是解析几何中常见的一类考题，该类问题一般假设存在，若能够推出所要结论，则可知假设正确，否则假设错误.

一、是否存在点

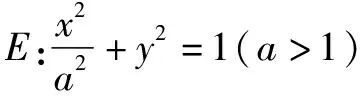
(1)求E的方程；

(2)设PA与E的另一交点为D，PB与E的另一交点为C，问：是否存在点P，使得四边形ABCD为梯形，若存在，求点P坐标；若不存在，请说明理由.

①

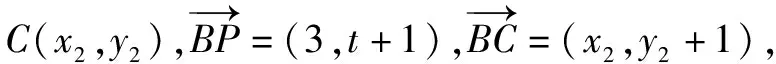
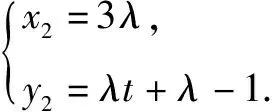
②

由①-②,得λ(λ-1)(3-2t)=0，且λ∈(0，1).

法2假设存在点P满足题设，则t>0，设C(x1，y1)，D(x2，y2).

点评是否存在点的问题，一般假设存在，再采用“肯定顺推法”，将不确定性问题明朗化.通过题目中的已知条件，建立关系，最终求解.

二、是否存在直线

(1)求圆C的标准方程；

(2)设过点M(0，3)的直线l与圆C交于不同的两点A，B，以OA，OB为邻边作OADB(O为坐标原点).是否存在这样的直线l，使得直线OD与MC恰好平行？如果存在，求出l的方程；如果不存在，请说明理由.

又S=πR2<13，所以a=1，R=2.

所以圆C的标准方程为(x-1)2+y2=4.

(2)当斜率不存在时，直线l为x=0，不满足题意.

当斜率存在时，设直线l：y=kx+3，A(x1，y1)，B(x2，y2)，又l与圆C相交于不同的两点，联立,得

消去y,得(1+k2)x2+(6k-2)x+6=0.

所以Δ=(6k-2)2-24(1+k2)=12k2-24k-20>0.

点拨利用向量解决圆锥曲线问题能够有效简化运算，在处理圆的综合问题时，首先要考虑使用数形结合思想进行解题，这样能够让问题变得非常直观化.

三、是否存在参数

(3+4k2)x2-8k2mx+4k2m2-12=0.

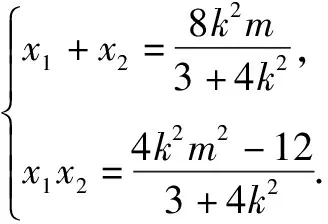
|MA|2+|MB|2=(1+k2)[(x1-m)2+(x2-m)2]

=(1+k2)[(x1+x2)2-2x1x2-2m(x1+x2)+2m2]

此时|MA|2+|MB|2=7与m无关,符合题意.

点评解决圆锥曲线的参数存在性问题，关键要在理解圆锥曲线的定义和性质下，根据题意，设出未知点和未知方程，通过联系韦达定理和题干要求，建立等式方程，进而可求得参数的值或范围.