基于PE-局部最优算法在基金智能定投领域的研究
2021-08-05何雨欣于祥雨
何雨欣,于祥雨,2,夏 羽
(1. 杭州师范大学数学学院,浙江 杭州 311121; 2. 华院计算技术(上海)股份有限公司,上海 200436)
基金定投是基金定期定额投资(automatic investment plan for mutual fund, AIP)的简称,即在固定的时间以固定的金额投资到指定的开放式基金中.M.S. Simpson[1]指出基金定投的性质类似于银行储蓄的零存整取理财方式.
关于基金定投的风险收益特征以及与普通定投相比的优劣性,国内外学者展开了不同的算法研究.国内文献中,胡阳等[2]提出了基于市盈率的基本面策略,给出了基金定投存在较好的风险收益特征的数学证明.相比于基金定投,智能定投是一种基于基金定投的优化投资策略.陈靖和[3]通过智能投资方法的3年期数据回测,对移动均线法则、市盈率(PE)法则以及止盈法进行收益率和风险的回测,得出PE法则适用于指数基金,止盈法适用于权益类基金和指数基金.周晓君[4]运用普通定投策略,3种基础智能定投策略(移动平均成本法、均线偏离定法、市盈率法),对随机选出的8支基金进行3个长中短考察期的模拟交易操作,以累计收益率、下行标准差以及索提诺比率作为评估参数,统计各期各基金收益及风险.唐福全[5]提出了基金定投双随机模型,从理论角度分别建立了服从不同分布的基金定投收益现值的离散模型和连续模型以及Markowitz风险评估方法,不过该模型缺乏数值验证.程喆源[6]研究了基于2007—2014年之间的部分基金作为一系列股票的证券组合,采用基金净值线与平均成本线的相互关系以及年化收益率来评价定投的盈亏和绩效,并且尝试了用目标收益法和技术分析法来优化定期定投策略.
国外文献中,Chen等[7]将绝对半偏差作为一种新的风险度量方法应用于投资组合优化,建立了3类模糊投资组合优化模型,通过数值实验验证了该方法的有效性.Chen等[8]用蒙特卡洛模拟算法考察了3种定投策略(普通定投法、平均价值算法和比例再平衡算法),得出高频率的价值平均算法的收益最好,然而该算法的风险也比较高.Fang等[9]提出平均成本法(DCA)是一种常见而有用的系统投资策略,更适合于应用投资标的资产风险较大,因其具有显著的能力对冲风险.蒙特卡洛仿真结果表明,DCA策略在降低风险方面优于一次性投资策略(LS),在投资回报方面劣于LS策略.
本文提出了一种新的基金智能定投算法,即 PE-局部最优算法(以下简称“智能定投”).针对2010-11-23—2015-09-29 的 3 支股票型基金、股票型平均、混合型平均以及沪深 300 指数共6支基金数据,本文对智能定投算法与普通定投算法进行了数据挖掘[10]和数值实验.结果表明,智能定投算法优于普通定投算法,具体体现如下:1)购买份数更多.最小购买份数多 4.04%,最大购买份数多 6.55%,平均购买份数多 5.13%.2)收益更高.智能定投收益较普通定投收益最多增长了7.22%,最少增长了1.80%,平均增长4.86%.3)最大回撤普遍更低.最大回撤率差值最大为 3.08%,最小为0.26% ,平均最大回撤差值达到1.12%.因此,相比于普通定投,智能定投更具有实用意义.
1 平均成本及收益、风险指标
1.1 平均成本
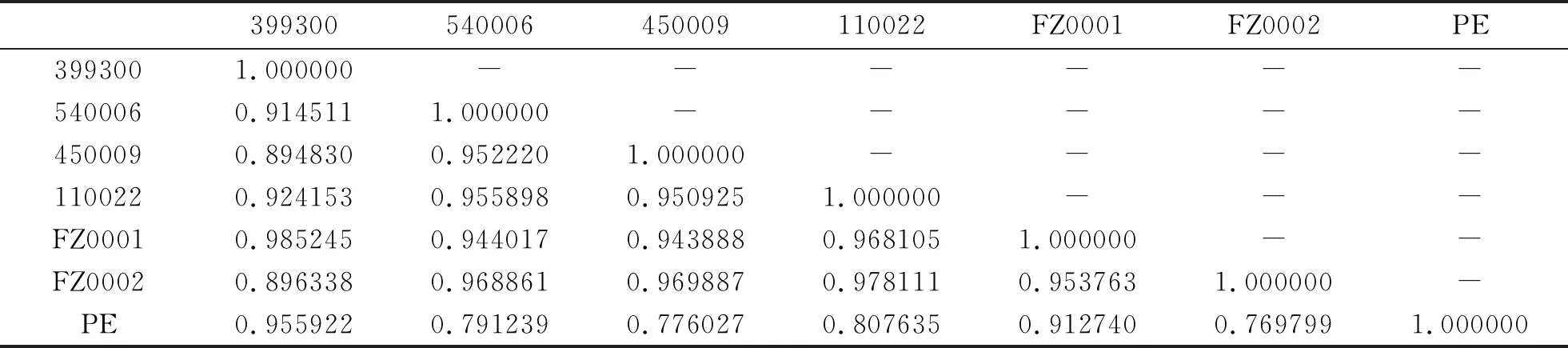
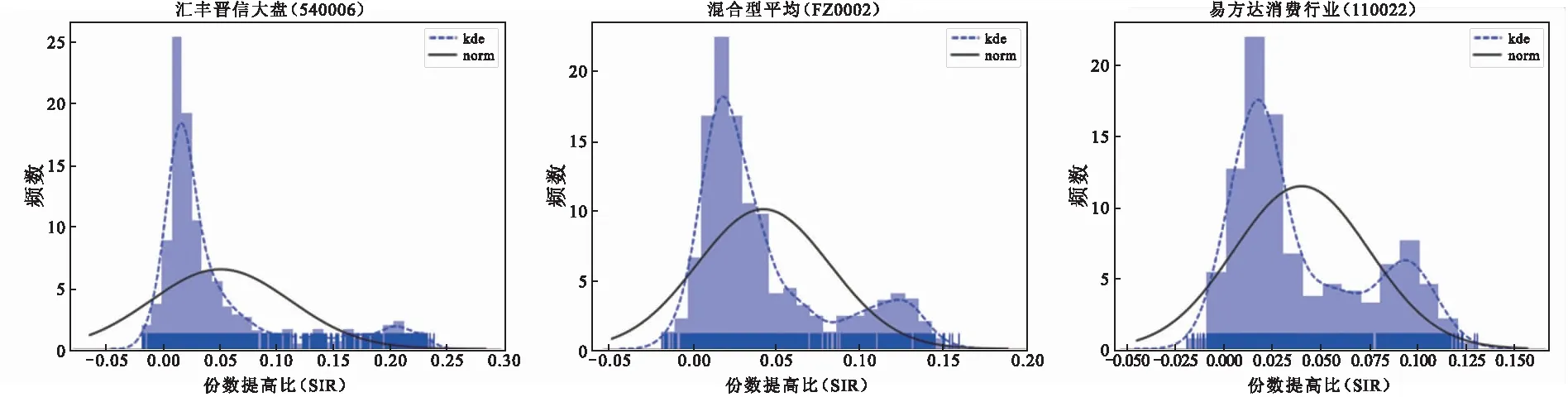
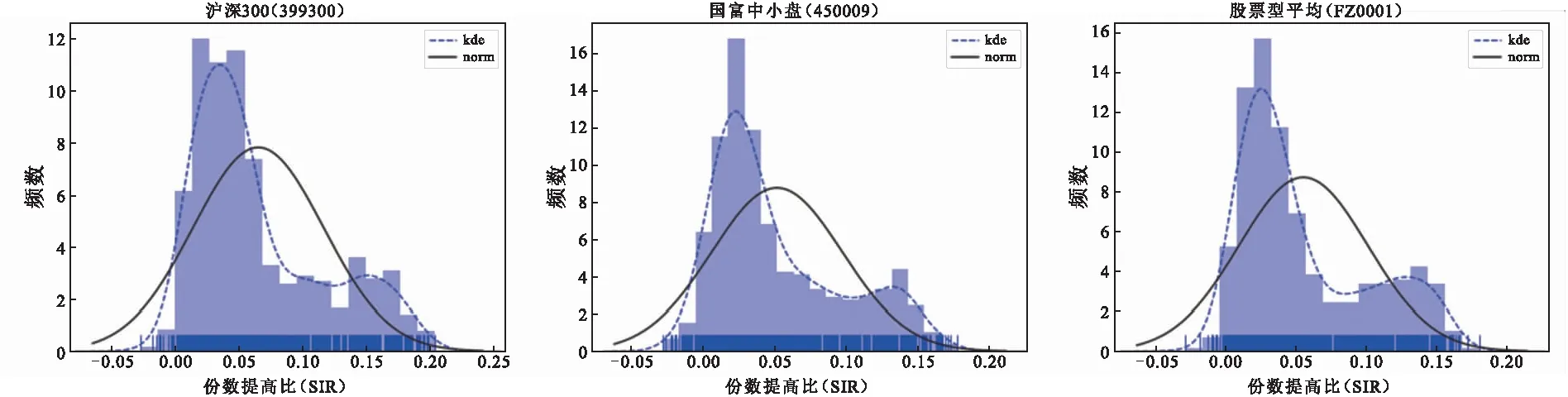
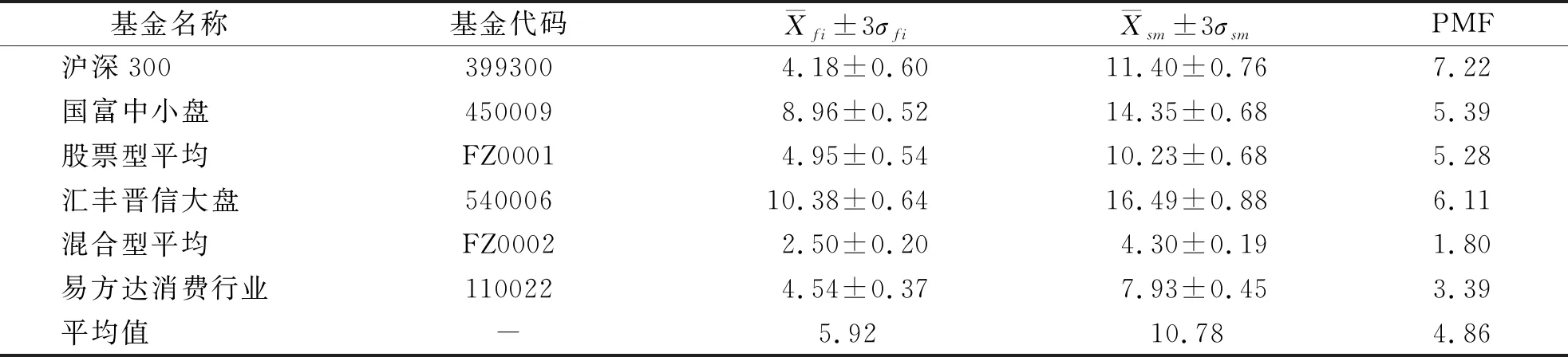
定投平均成本是指定投基金的平均单位净值,其实质是各时段基金单位净值倒数的算术平均数的倒数,即调和平均数.假设针对某支基金实行定投,总共投资 1 个单位的资金,分N期进行定投,每期投资金额均为1/N,则截至第k(0 (1) 其中,pi表示第i期对应的基金净值.显然,当截至第N期的平均成本ACN的值小于第N期的基金净值pN时,则基金定投处于盈利状态,反之,则处于亏损状态. 智能定投指在总投资资金不变的基础上,每期投资金额可选取不同数值.类似地,其智能定投截至第k(0≤N)期基金智能定投的平均成本为SCk, (2) 其中,wi表示第i期对应的投资金额数量(wi>0).显然,若SCk小于ACk,则说明智能定投更有优势. 由于无法确定wi的具体数值,直接通过平均成本来比较两种投资方式的优劣存在一定难度.因此,本文设置了相同的投资金额,通过比较购买基金份数、收益、风险等来比较两种投资方式的优劣.本文构建了5个比较两种投资方式优劣性的指标,分别是:智能定投份数(smart timer invest, STI)、智能-定投份数差(smart-timer invest difference, STID)、份数提高比(share increase ratio, SIR)、最大回撤差值(margin of maximum drawdown rate,MMDR)和收益差值(profit margin of fund, PMF). 定义1(智能定投份数,STI) 假设总共投资1个单位的资金,共投资N期,则 (3) 定义2(智能-定投份数差,STID)假设投资1个单位的资金,共投资N期,则有 (4) 定义3(份数提高比,SIR)假设S是传统基金定投方式在相同条件下购买的基金份数,则份数提高比为 (5) 其中,S是传统基金定投方式在相同条件下购买的基金份数. 定义4收益差值(PMF)指智能定投的收益(revenue of smart invesment, RSI)与普通定投的收益(revenue of fixed invesment, RFI)的收益差值:PMF=RSI-RFI. 定义5最大回撤差值(MMDR)是指智能定投的最大回撤率(maximum drawdown rate of smart invesment, MDRSI)与普通定投的最大回撤率的差值(maximum drawdown rate of fixed invesment, MDRFI):MMDR=MDRFI-MDRSI. 金融市场千变万化,影响因素不计其数,仅通过基金的历史数据无法精确地预测出基金未来的具体净值.然而从统计学角度分析,基金的历史数据可以在一定程度上衡量基金的稳健程度、净值变化趋势,因此历史数据具有使用价值.再者,股票型基金、混合型基金(股票市场资产配置比重大的混合型基金)受 PE 值影响较大,即存在一定的正相关性,根据历史的 PE 值和数据表现情况,可以评估出未来的短期变化趋势. 相比于其他学者的研究算法,本文算法的突出优点在于考虑了当前市盈率条件下的投资方式对下一个投资日期的影响,通过历史上证市盈率变化趋势、涨跌幅度并结合统计学[11]与机器学习[12]原理,提出局部最优策略.为满足STIDN取值最佳,本文结合图1和图2来阐述局部最优策略. 某支基金的历史净值如图1所示,计划投资N期,由于各个投资期的净值已知,通过式(1)、(2)和(4)可分别计算出基金普通定投的平均成本、智能定投的平均成本和智能定投购买的总份数.例如,指定第 1 期投资日期,获得该日期对应的上证市盈率(PE),统计处于区间(PE-α,PE+α)内的上证市盈率所对应的时间点,并观察对应的基金净值的变化情况.更具体地,以易方达消费行业基金为例,指定 2017年09月11日作为第1期投资日期,其对应 的PE为16.27,设α=0.5,统计落在区间(15.77,16.77)内的上证市盈率所对应的时间点,共有m=309个.从 309 个时间点中随机选择 4 个样本数据,观察样本数据在时间跨度为 1 年的基金净值变化情况,如图2所示. 图1 定投策略流程图 图2 部分满足PE条件时间跨度为1年的基金净值 本文算法的难点在于固定投资期数(N)条件下确定每期的投资资金或总投资资金的比例(wi,i=1,2,…,N),是一个维度为N的问题,通常N≥12,显然这是一个高维度问题,求解式(4)的解析解困难较大,而由Nicholas等[13]提出的蒙特卡洛法可以有效处理高维度问题.蒙特卡洛法,或称统计实验方法或随机抽样方法,是一种基于“随机数" 的计算方法.Yves[14]提出蒙特卡洛模拟是金融学和数值科学中最重要的算法之一,常用于解决期权定价或风险管理等实际问题,他给出了3种利用蒙特卡洛法生成随机数或随机向量的计算方法.基于此,本文通过蒙特卡洛法求解式(4)的近似解. 在本小节中,假设对基金A进行智能定投,设定计划总投资金额为1个单位,共投资N期,每期间隔1个月.若投资日期处于节假日,则选择在假期后的第一个交易日作为投资日期.下面给出算法的伪代码: 算法1PE-局部最优算法 Require: (输入) 基金A的历史复权净值数据,上证市盈率pe的历史数据,参数α,τ. 随机权重矩阵行数r,计划投资期数N,总资金为IM=1单位. Ensure:(输出) 1) 令HM1=IM 2) fori(i=1,2,3,…,N) do 3) 索引基金A在第i期对应的pei值,并根据给定的α,计算出PEi. 8) forq(q=1,2,…,r) do 10) end for 12) end for 15) end for 16) return 为验证本文提出的智能定投算法优于普通定投算法,选取6支基金进行数值实验.通过比较购买份数、年化收益率和最大回撤等指标,对这两种算法进行客观分析.数值实验采用的数据从2010 年11月23日至2015年9月29日,且PE 数据是每个投资日之前的PE历史数据.将每个时间点作为起始投资日期,为期1年,投资期数为12(总投资金额IM为1,α=0.05,采用月定投),进行1 126次数值实验. 通过3支股票型基金(包括汇丰晋信大盘、国富中小盘和易方达消费行业)、沪深300指数、股票型基金的平均指数和混合型基金的平均指数进行实验.股票型基金以投资股票市场为主;股票型平均指数基金是对所有公开发行的股票型基金的指数概括;混合型平均指数基金是对所有公开发行的混合型基金的指数概括;沪深300指数是由沪深证券交易所从市场中选取300只A股作为样本,具有良好的市场代表性.以上6支基金的基本信息如表1所示. 表1 基金的基本信息 采用表1的6支基金作为数值实验的对象,利用皮尔逊相关系数[15]对上证市盈率(PE)与 6 支基金进行相关性分析,其结果如表2所示. 由于智能定投算法依赖 PE 值,因此基金净值与 PE 值的正相关性较强时,说明该基金适用于本文的智能定投算法.如表2所示为6支基金和 PE 指数的相关性分析:1)沪深300(399300)、股票型平均(FZ0001)与PE正相关,相关系数分别为0.955922和0.912740;2)混合型平均(FZ0002)、国富中小盘(450009)与PE弱相关,相关系数分别为0.769799和0.776027. 表2 PE与实验对象的相关性系数 各基金中,如果一组基金之间的相关性呈现高度正相关,往往它们与PE值的相关性也基本保持一致.如表2所示:沪深300(399300)与股票型平均(FZ0001)高度正相关,相关系数为0.985245,它们和 PE 值的相关性都属于高度正相关;混合型平均(FZ0002)与国富中小盘(450009)高度正相关,相关系数为0.969887,它们和PE值的相关性都比较弱. 本小节主要阐述数值实验的其他方法和指标. 定义8(非线性衰减函数, nonlinear decay function, NDF) 假设剩余投资期数为N,那么 NDF=[ep×N+q]. (6) 其中,[·] 表示向上取整,p,q为给定参数.本文令p=0.618,q=100. 数值实验结果见表3,P(STID>0)都在90%以上,说明智能定投优于普通定投.P(STID)≥0 的理论值应为100%,由于式(6)中p,q取值并非最优,即蒙特卡洛法次数不足,若p,q设置过大会增大计算量.用公式(4)和(5)量化两种定投的差异,如图3所示. 图3 实验结果直方图(α=0.05,τ=1e-5) 表3 2010-11-23—2015-09-29 期间的实验结果 续表3 如图3所示,各基金的KDE曲线规律有:1)各基金的 KDE 峰值都位于正态分布线峰值的左侧;2) 除了汇丰晋信大盘,其余基金的 KDE 曲线都有两个峰值,各峰值所对应的SIR都分别位于(0,0.05)和(0.10,0.15);3)各基金SIR低于0 的频数很小.各基金的正态分布曲线(norm)规律如下:1)除了易方达消费行业基金,其余5支基金的中心位置μ均在0.05附近;2)易方达消费行业基金最陡峭,标准差为0.034905,汇丰晋信大盘基金最平缓,标准差为0.061635. 3.3.1α取值对算法的影响 以沪深300(399300)基金为例,采用不放回随机抽样方法从 1 126 个数据中抽取 30 个样本进行数值实验,探索α对份数提高比(SIR)、P(STID>0)的影响. 如表4所示:1)随着α的升高,份数提高比(SIR)先上升后下降;2)随着α的升高,P(STID>0)先上升后下降;3)随着α的升高,SIR的标准差先下降后上升,说明α的取值影响份数提高比的稳定性;4)随着α的升高,CV系数一直上升.实际应用中,若α取值过小,会导致缺失统计学意义,若α取值过大,会导致SIR和P(STID>0)降低. 表4 沪深300在不同α下的实验结果 如图4所示:1)当α取值过大,各支基金的SIR和P(STID>0)曲线普遍呈现下降趋势;2)不同α下,SIR和P(STID>0)显著不同. 图4 α取值在不同基金下的结果 3.3.2 收益分析 以沪深300指数为例,对收益与基金净值归一化处理,如图5所示,收益曲线代表各定投下总收益和投资总成本之和,PE值代表第一期投资日期对应的PE值. 图5 沪深 300 指数的收益分析图 如图5所示,不同的PE值下:1)智能定投的收益曲线总高于普通定投;2)当PE=12.02时,两者收益曲线的波动幅度基本一致;当PE=21.77时,前者收益远高于后者. 各个基金收益均值的数值统计分析如表5所示:1)混合型平均(FZ0002)的收益表现最差,其普通定投和智能定投的年化收益率分别为(2.50±0.20)%与(4.30±0.19)%;2)汇丰晋信大盘(540006)的收益表现最好,其年化收益率分别为(10.38±0.64)%与(16.49±0.88)%;3)由PMF 指标,混合型平均(FZ0002)的收益差值最不显著,其PMF指标为1.80%,沪深300(399300)的收益差值最显著,其PMF指标为7.22%.4)综合而言,智能定投的年化收益率普遍高于普通定投,智能定投下的平均年化收益率高达10.78%,远高于普通定投的5.92%,平均PMF指标为4.86%. 表5 各支基金收益均值分析表(α=0.05,N=12,τ=1e-5) 3.3.3 风险分析 最大回撤反映投资者可能面临的最大亏损幅,用于评判某基金的风险控制能力[18].如表6所示,本小节给出各支基金的风险分析. 表6 最大回撤的风险分析(α=0.05,N=12,τ=1e-5) 表6是从最大回撤角度给出智能定投与普通定投的对比结果.本文算法与普通定投算法,混合型平均(FZ0002)的最大回撤最低,其普通定投和智能定投的最大回撤平均值分别为8.11%和6.84%,普通定投下,沪深300的最大回撤平均值最高,达到13.92% ,智能定投下,国富中小盘(450009)的最大回撤平均值最高,达到13.51%.而通过MMDR指标衡量两种算法的风险性时,易方达消费行业(110022)的最大回撤差值最不显著,其MMDR指标为0.26%,沪深300(399300)的最大回撤差值最显著,高达 3.08 %.综合而言,本文算法在 6 支基金上的最大回撤平均值普遍低于普通定投算法的最大回撤平均值,并且平均普通定投最大回撤平均值达到 11.98%,远高于平均智能定投下的最大回撤平均值的 10.86%,平均MMDR指标为1.12%. 由表6易得:1)各支基金的最大回撤率相比于本文算法而言均较高,即本文算法在基金上的最大回撤均小于普通定投;2)不同基金的最大回撤平均值不同,即不同基金存在不同的风险;3)“高收益对应高风险”,然而本文算法可以在获得较高收益(相比普通定投)的情况下,尽量降低风险(相比于普通定投),更能体现智能定投的优势. 本文通过对上证市盈率(PE)进行数据挖掘,提出一种基于PE的局部最优算法.通过智能定投和普通定投的数值实验对比分析,智能定投优于普通定投,具体表现为:平均购买份数提高 5.13%,收益平均提高4.86%,风险(最大回撤)平均降低1.12%. PE的作用有:1)寻找区间落在(PE-α,PE+α)的上证市盈率所对应的时间点数量个数,从这些时间点个数中随机批量抽取,分别作为新一期的基金智能定投起始点;2)设置合适的PE区间.传统的PE估值法是在PE高位买入,PE低位卖出,但PE估值法并不能找到一个合适的区间,并且PE的高低并不能准确预判基金净值的高低;3)预判实验者所选取的基金是否适合本文算法,对于与PE呈高度正相关的基金适合本文算法,否则放弃该基金. α是人工参数,α对SIR和P(STID>0) 的结果影响显著.当α值过小时会失去统计学意义,当α值过大时会降低PE的灵敏度. 本文在探索不同α下对SIR和P(STID>0)的影响时,采用不放回抽样方法随机抽取 30 个样本,由于其实验条件有限,因此其结果可能并非最佳.其次,α的取值对不同基金有一定的影响,但是影响程度较小,投资机构或个人可以根据本文算法对指定基金进行数值实验,估算出相对较好的α.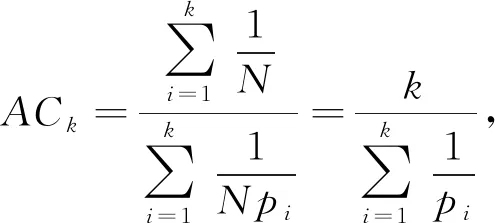
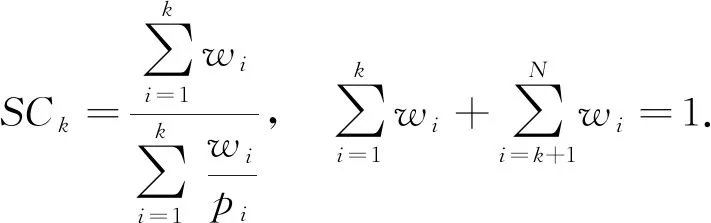
1.2 收益、风险指标





2 PE-局部最优算法
2.1 局部最优策略


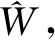
2.2 算法伪代码


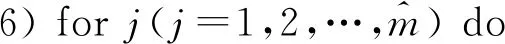




3 数值实验
3.1 实验数据集与实验条件

3.2 实验方法




3.3 结果分析






4 结束语
