捕食者具有Allee效应的时滞捕食-食饵系统的稳定性与Hopf分支
2021-08-05宋永利
陈 璐,宋永利
(杭州师范大学数学学院,浙江 杭州 311121)
0 引言
捕食者与被捕食者(食饵)之间的相互关系是自然界中种群之间最基本和普遍的关系之一,是维持生态平衡、物种繁衍和生物多样性的基本生态系统.对捕食-食饵系统的动力学的定性研究也是生物数学领域研究的基本问题之一.建立合理的数学模型是定性分析的基础.Logistic方程是描述种群增长的最常用数学模型,该模型表示种群的单位增长率随着种群数量的增加而减少.然而,对于在资源稀缺情况下,种群数量比较少时,种群数量的增加有利于互惠捕获、协作觅食、繁衍后代,在这种情况下种群的单位增长率随着种群数量的增加而增加,生物上称这种现象为Allee效应.
近年来,对于Allee效应对种群动力系统的影响的研究引起了生物、生态和生物数学领域诸多学者的关注[1-3].特别是在文献[3]中, Stephens和Sutherland发现在生物种群数量较少的情况下, Allee效应会增加种群局部和全局灭绝的可能性.这些研究工作都是关于食饵种群中的Allee效应对捕食-食饵系统的动力学的影响.但是在现实生活中,捕食者种群通常比食饵种群数量小很多,所以捕食者种群比食饵种群更容易受到Allee效应的影响[4].文献[5]指出,在需要通过调节捕食者幼年期的成熟速率,使其更快到达成熟期的捕食者会具有Allee效应.然而关于捕食者的Allee效应对系统动力学行为的影响的理论研究工作相对于食饵种群的Allee效应的相关研究还很少.
考虑到捕食者的Allee效应, Zhou等[1]建立了以下捕食-食饵系统:

(1)

大量的生物统计数据表明,当捕食者种群密度比较小的时候,捕食-食饵系统仍然可以在较长时间维持一种平衡态[6].因此,系统(1)中正平衡点始终是不稳定的结论和大多数的生物系统并不相符.Bodine等[6]基于捕食者数量的增加将会导致捕食者的种内竞争的假设,在系统(1)中引入捕食者的种内竞争机制,建立了如下模型:
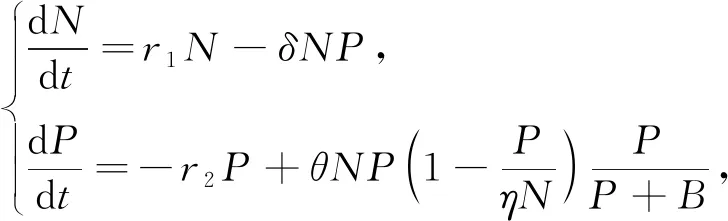
(2)

由于种群的孕育期,当前时刻的种群增长率总是与某个时刻之前的种群数量有关.这种由于孕育期而导致的时滞现象在种群动力学中普遍存在,并且时滞往往会导致平衡态失稳[10-12].如果考虑环境最大容纳量和食饵种群繁衍的孕育期,系统(2)为以下时滞捕食-食饵系统:
其中K表示最大环境容纳量,τ≥0称为时滞.
为了简化参数,引入无量纲变量
和无量纲参数
并在变换之后去掉波浪号以简化符号,得到以下系统:

(3)
其中τ≥0,a≥0,其余参数全都为正数.
在下边的部分,我们主要研究系统(3)的正平衡点的存在性、稳定性以及时滞对正平衡点的稳定性的影响.
1 无时滞情况下系统(3)的非负平衡点的存在性及其稳定性
1.1 非负平衡点的存在性

当a>0时,假设E*(N*,P*)是系统(3)的一个正平衡点,则有P*=1-N*<1,且P*是下面一元二次方程的正根:
(b+c)P2+(d-b)P+ad=0.
(4)
因此,系统(3)的正平衡点的个数由方程(4)的介于0和1之间的正根个数所决定.
定理1(Ⅰ) 如果0
(Ⅱ) 如果b>d>0,且a,c>0,我们有以下结论:

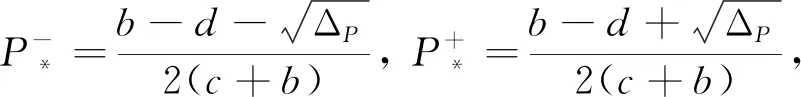
(5)
其中ΔP=(d-b)2-4ad(b+c).
证明(Ⅰ) 当0
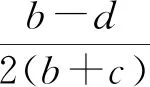
(b+c)P2+(d-b)P+ad=c+d+ad>0.
因此,在这种情况下若方程(4)存在正根,则一定会小于1.
此外,通过简单的计算,我们发现方程的判别式(d-b)2-4ad(b+c)=0成立当且仅当

□
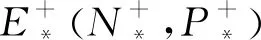

1.2 非负平衡点的稳定性
当τ=0时,系统(3)为以下常微分方程组

(6)
假设(N*,P*)是系统(6)的平衡点,那么对应的特征矩阵为A=(aij)2×2,其中
特征方程为
λ2-Tr(A)λ+Det(A)=0,
(7)
其中Tr(A)=a11+a22,Det(A)=a11a22-a12a21.
定理2系统(2)的零平衡点E0(0,0)是一个鞍点,边界平衡点E1(1,0)是一个稳定的结点.
证明首先,对于平衡点E0(0,0),可以求出方程(7)的两个根,分别为λ1=1和λ2=-d,所以,平衡点E0(0,0)是一个鞍点;
对于平衡点E1(1,0),也可求出方程(7)有λ1=-1和λ2=-d两个根,所以,平衡点E1(1,0)是一个稳定的结点.
□
如果(N*,P*)是系统(6)的正平衡点,则有
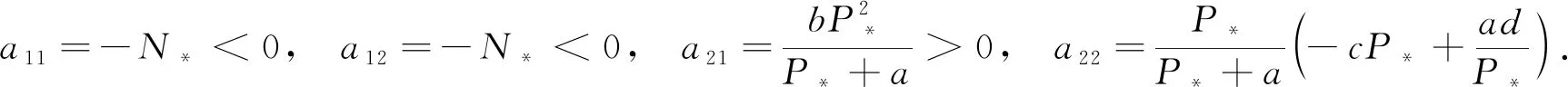
(8)
特别地,当a=0,c>0,b>d>0时,我们有
a11=-N0*,a12=-N0*,a21=-bP0*,a22=-cP0*.
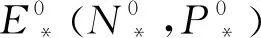
当a,c>0,b>d>0时,由式(8)得
再由式(4)和(5),可得
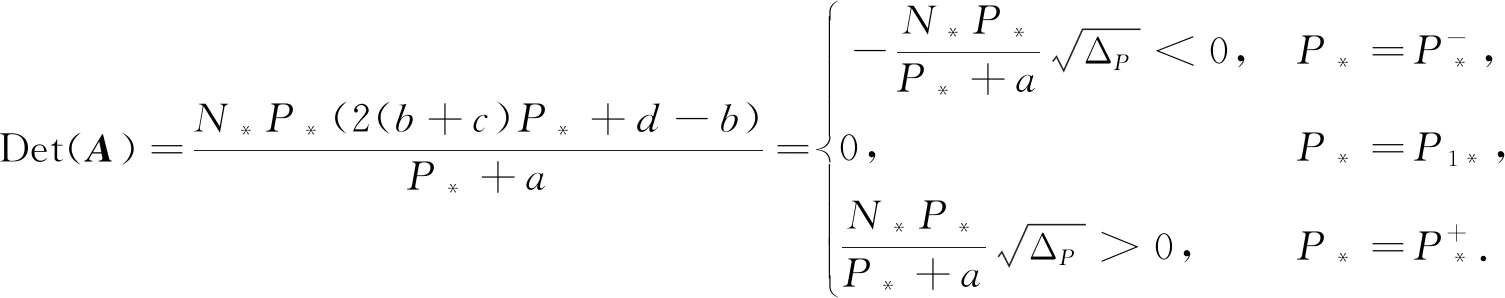
(9)

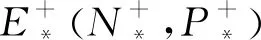


□
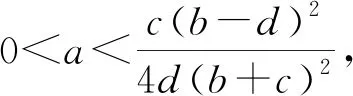
证明令
那么系统(3)的正平衡点的存在性可以直线N=N1(P)和曲线N=N2(P)在P-N平面上的交点个数决定,其中P∈(0,1).
再结合表达式(8),有
和
□
2 时滞对正平衡点的稳定性的影响


(10)
线性化系统(10)的特征方程为
λ2-a22λ-(a11λ-a11a22)e-λτ-a21a12=0.
(11)
根据本节的基本假设,当τ=0时,方程(11)有两个具有负实部的根.下边我们分析当τ>0时,方程(11)根的分布.由于方程(11)的根依赖于时滞,且关于τ连续变化.因此,方程(11)的根随着τ的变化,要从左半平面到达右半平面,必然在τ的某个值处到达虚轴.另外,由Det(A)>0,易见对于任意的τ≥0,λ=0不是方程(11)的根.下边我们寻求方程(11)有一对纯虚根的条件.假设λ=iω(ω>0)是方程(11)的一个根,把它代入方程(11),可得
-ω2-a22iω-(a11iω-a11a22)(cosωτ-isinωτ)-a21a12=0.
(12)
分离方程(12)的实部和虚部,有

(13)
即
ω4+Bω2+C=0,
(14)

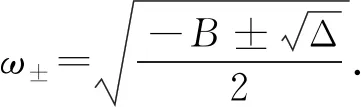
(15)
若设ω±>0,则由式(13)可得

(16)
因此,由式(15)和(16),可计算出对应的τ值
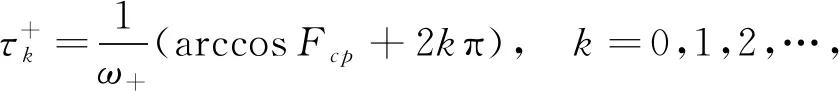
(17)
和

(18)
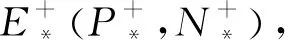
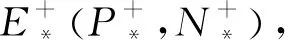
因此,由上式易见当Tr(A)<0时,Fsn≥0的充要条件为a22≤a11.
当a22≤a11<0时,Fsn≥0,且由式(16)可得Fcn 当a22>a11时,Fsn<0.又因为Fsp>0,易知 □ 证明对等式(11)两边分别关于τ求导,可以得到 因此, □ 方程(14)有两个正根、一个正根和没有正根3种情况.则由引理2、引理3和微分方程定性理论,有以下结论. 下边利用数值分析,在参数a-b平面上的区域 R={(a,b)|0 曲线f2,f3分别为C=0和Δ=0.如图1所示. 图1 方程(14)的正根个数分布区域 (A) (A) 在本文中,我们主要研究了捕食者的Allee效应和食饵的孕育时滞对捕食-食饵系统的正平衡点的存在性及稳定性的影响.捕食者不具有Allee效应时,系统(3)存在唯一的一个正平衡点.当捕食者存在Allee效应时,存在一个临界值,当Allee效应强度小于这个临界值时系统存在两个正平衡点,当Allee效应的强度大于这个临界值时系统没有正平衡点. 在系统没有时滞的情况下,无论捕食者是否具有Allee效应,边界平衡点(1,0)始终是局部渐近稳定的.这个平衡点对应于捕食者种群的灭绝.当捕食者没有Allee效应时,系统(3)存在唯一的一个稳定的正平衡点.当捕食者存在Allee效应时,存在一个临界值,当Allee效应强度小于这个临界值时系统存在两个正平衡点,其中捕食者密度较小的正平衡点是鞍点,捕食者密度较大的正平衡点的稳定性依赖于Allee效应的强度大小,当Allee效应的强度较小时这个正平衡点也是稳定的.然而,当Allee效应的强度大于上述临界值时系统没有正平衡点.这意味着当捕食者种群的Allee效应强度比较弱时,捕食者的相互协作有利于其生存,并和食饵种群达到和平共处的状态.然而,当捕食者的Allee效应强度过大时,捕食者种群的单位增长率会出现负值,最终将会导致捕食者种群的灭绝. 进一步,在正平衡点稳定的条件下,我们研究了食饵种群的孕期时滞对其稳定性的影响.研究发现,时滞对正平衡点稳定性的影响依赖于捕食者的Allee效应强度与其对捕获的食饵种群的消化率之间的关系.在以捕食者的Allee效应强度和捕食者种群的消化率组成的参数平面上存在着3类不同的区域:时滞不改变系统正平衡点稳定性的区域; 时滞导致正平衡点失去稳定性并发生Hopf分支的区域; 以及时滞导致稳定性开关并发生Hopf分支的区域.因此,食饵种群的孕期时滞对系统的动力学行为具有重要的影响,会导致正平衡点失稳,并在正平衡点附近产生小振幅的周期振动现象.这与实际的生物现象更加贴近.



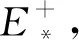

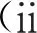
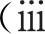


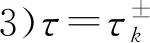
3 数值模拟


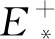
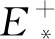

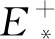

4 结论
