顺应式海洋平台慢漂运动物理模型试验研究

金瑞佳，张崇伟，柳 叶，耿宝磊，郑艳娜

(1. 交通运输部天津水运工程科学研究所，天津 300456； 2. 中国海洋大学 工程学院，山东 青岛 266100； 3. 大连海洋大学 海洋与土木工程学院，辽宁 大连 116036； 4. 天津大学 建筑工程学院,天津 300072)

人们对能源的需求日益迫切，陆地的传统油气资源已经难以满足人们的需求，深海海洋油气开发成为各国能源战略的一个重要保障。浮式平台依靠自身浮力来支撑上部结构，加上锚链系泊，适合在深海勘测开采。深海中的大型浮体结构物通过锚泊系统定位于海中，此时，浮体结构系统在水平运动方向通常具有很低的固有频率，特别容易在非线性波浪差频的作用下激发共振而发生大幅度的水平往复慢漂运动。当漂移距离过大时，存在一定的安全隐患，对平台的生产作业有较大影响。

对于浮体的慢漂运动，很多学者对此进行过研究，Agnon等[1-2]通过二维漂浮方箱的慢漂运动的研究给出了小幅值慢漂和大幅值慢漂的解析解。随后，Ohyama和Hsu[3]基于势流理论采用完全非线性的边界条件同样模拟了该方箱的慢漂运动，并与Agnon等[2]吻合良好。王依娜等[4]采用高阶边界元方法，考虑了海底地形在波浪传播中对其的绕射影响计算海底地形对浮体慢漂响应的影响。计算结果表明,变浅的海底地形会导致波浪场的波高增加,浮体运动响应增大，说明在模拟近岸水动力情况时不能忽略地形影响。姜宗玉等[5]基于势流理论研究了动力定位半潜式平台在不规则波中的慢漂响应。通过对不同海况下计算结果的对比，发现平台承受的二阶漂移力幅值主要由波幅决定，较大的漂移力会产生较大慢漂运动，平台慢漂运动明显受慢漂阻尼以及动力定位系统的影响。Faltinsen和Zhao[6]研究了不规则波作用下的二维物体的慢漂运动。Kim和Lim[7]介绍了一种设计波浪方法，用于估算系泊浮式海上平台在极端条件下的极限水平慢漂运动。该方法已应用于深水半潜式平台，与全长度非线性仿真模拟结果相比，具有良好的应用前景。除了数值模拟，还有学者对慢漂现象进行物理模型试验研究。Molin等[8]和Liu等[9]对海底有坡度情况下的系缆矩形驳船在不规则波作用下的慢漂运动进行了物理模型试验研究，并将试验数据与数值结果对比，分别比较了平均漂移位移和漂移的标准差，发现在水深较深情况下，数值结果和试验结果吻合良好。王磊等[10]对一艘动力定位船舶二阶低频慢漂力进行了模型试验,并将试验得到的纵向和横向慢漂力谱与势流理论方法得到的理论值进行比较,结果表明,该模型试验方法与理论计算较为吻合。

近年来，学者对实际海洋工程结构物的慢漂运动进行了分析，金瑞佳[11]提出两次展开方法求解系泊浮体的大幅慢漂运动，该方法对基于初始平衡位置的摄动展开方法进行了改进，适合于浮体发生大幅慢漂运动时的计算，并计算了系泊Spar平台和系泊半潜平台的大幅慢漂运动。黄印等[12]基于三维势流理论和Morison公式，利用AQWA软件研究自升式平台在桩腿下放过程中的运动响应，发现平台在系泊定位状态下纵荡和横荡会发生大幅低频慢漂运动，并且随着桩腿下放长度的增加平台的运动幅度逐渐减小，当桩腿下放长度超过35 m时平台垂荡运动的变化不再明显。Lupton和Langley[13]计算了浮式风机的慢漂运动，并推导了平台尺寸、锚泊系统和波浪条件与慢漂运动的近似表达式。Yazid等[14]通过对Truss Spar平台的纵荡传递函数进行分析，并对该传递函数进行了数值和试验验证。

上述模拟大多采用数值方法进行模拟，而进行的物理模型试验较少，为了深入分析浮体慢漂运动的影响，在水池中进行系泊浮体在不规则波作用下慢漂运动的物理模型试验，分析不同波浪工况作用下不同形状浮体在不同系泊刚度约束下的慢漂运动响应，为实际海洋工程以及数学模型的建立和验证提供有效的试验数据。

1 试验概况

1.1 模型布置

本次试验进行了浮式结构物的自由衰减试验和不规则波与系泊浮体相互作用试验。不规则波与系泊浮体相互作用试验分析了不同系泊刚度和不同浮体形状对其运动的影响。试验在波浪宽水池中进行。试验水槽长度为62.0 m，宽度为12.0 m，深度为1.2 m。试验所使用的造波机为电机伺服驱动推板式造波机，该造波机可以用于产生规则波与不规则波。为保持水池试验过程中模型两侧的水位保持不变，水槽两端均设置消波装置，同时在水池两端设连通管。试验选取截断圆柱和方箱作为研究对象，方箱尺寸为1.0 m×1.0 m×0.7 m(长×宽×高)，吃水为0.45 m，直立圆柱尺寸为直径1.0 m,高0.75 m，吃水0.45 m，距离造波机28.0 m。试验中波浪的入射角度为0°。试验中沿结构物周围从左往右依次旋转45°放置5、3、3、3、5个传感器，共19个波高传感器，结构物四周每排首个传感器间距为80 cm，其余传感器间距为40 cm，图1为坐标系及波高传感器布置图，顺浪向为x向，垂直浪向为y向。图2为模型实体照片。模型水位通过测针控制。模型中位移测量采用非接触式浮体运动量测量系统(六分量仪)，对浮体的运动响应进行同步测量，发射器固定在距浮体1米以上(不影响磁场)的木架上，接收器固定在方箱的顶部中心，以便定位和实时跟踪浮体六个自由度位移。模型中系泊系统由4组系泊线组成，水平布置在水面处，每组系泊线都由钢线和弹簧组成，其中钢线长度为0.3 m，弹簧长度为0.9 m，弹簧初始长度为0.5 m,从而保证浮体运动时各弹簧不会发生松弛现象，单根弹簧初始重量为0.12 kg，弹簧刚度为31.25 N/m，系泊角度为30°(如图1所示)，从而得到单弹簧约束下的顺浪向系泊刚度为54.13 N/m，双弹簧约束下的顺浪向系泊刚度为108.26 N/m。

图1 截断圆柱和漂浮方箱尺寸、坐标系及波高传感器布置Fig. 1 Dimension of truncated cylinder and floating square box、coordinate system and layout of wave height sensors

图2 模型实景照片Fig. 2 Model pictures in the physical model test

1.2 入射波浪场

本次试验水深为0.76 m。试验中波浪采用单向不规则波进行试验。不规则波的频谱采用Jonswap谱，其谱峰因子γ取3.3。

试验中，有效波高变化范围为0.090～0.206 m，波浪有效周期变化范围为0.8～1.4 s，具体组次见表1。

表1 试验波要素表

1.3 试验统计方法

1.3.1 位移分离方法

采用非接触式浮体运动量测量系统测量浮体在波浪中不同方向的运动响应时间历程曲线，对其进行分解，依据波浪的入射频率分解为一阶和二阶运动响应。假设i方向(i=x,z)测得的运动响应为ξi(t)，需对测量的ξi(t)进行Fourier变换：

(1)

式中:F表示Fourier变换，N表示Fourier变换的数据个数，ω表示Fourier变换的角频率；ξi(ω)表示位移时间序列的频域结果，表示该时间序列在不同频率下的能量分布。通过Fourier变换完成从时域到频域的转换，得到i方向浮体位移随时间的变化曲线的幅值谱曲线ξi(ω)，分析幅值谱曲线，分别选取一阶和二阶低频有效频率段，将其它无效频率段的幅值赋予0，保留有效频率范围内的数据，得到处理后的幅值谱曲线；再对处理后的幅值谱曲线进行Fourier逆变换：

(2)

式中：F-1表示Fourier逆变换，从而得到i方向的浮体一阶运动响应和二阶低频运动响应随时间的变化曲线。

1.3.2 位移统计分析

2 试验结果与分析

试验中，需要对实测位移分离后的一阶以及二阶低频位移结果进行分析。由于试验组次较多，以方箱在单弹簧约束时，组次I4(H1/3=0.206 m,TP=1.4 s)下的运动响应为例进行介绍。图3为该工况下无结构物时波面时间历程曲线，图4为放入漂浮方箱后，方箱纵荡方向的实测位移。

图3 无结构物时波面时间历程曲线(组次I4)Fig. 3 Wave elevation time history without structure

图4 漂浮方箱单弹簧约束时的实测位移曲线(组次I4)Fig. 4 Measured displacement time history of floating box restrained by single spring

然后对测得的波面高度以及运动响应时间历程曲线进行傅里叶变换，得到幅值谱曲线，见图5和图6，从图5中可以看出，试验得到的波浪谱和理论谱比较接近。

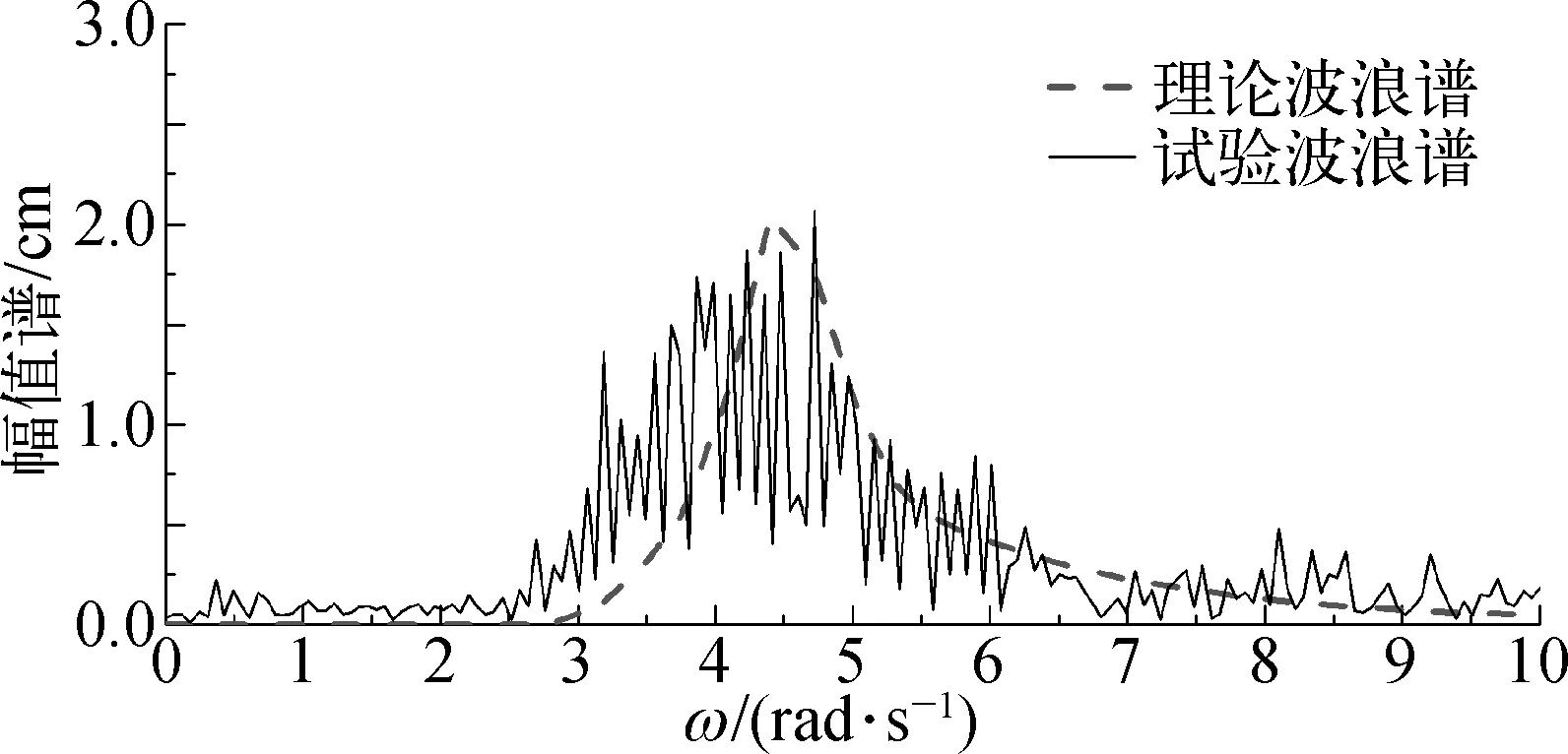
图5 波面高度幅值谱(组次I4)Fig. 5 Amplitude spectrum of wave elevation

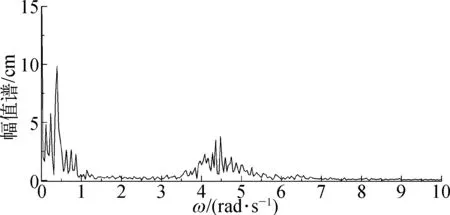
图6 运动响应幅值谱(组次I4)Fig. 6 Amplitude spectrum of motion response

从图6中可以看到在低频和波频部分有两个峰值，为获得这两部分的结果，结合图5的波面高度幅值谱，对低频部分取0.0～1.0 rad/s、对波频部分取2.5～7.0 rad/s，其余频率段的幅值赋予0，保留有效频率范围内的数据，再对处理后的幅值谱曲线进行Fourier逆变换，分别得到一阶波频和二阶低频运动响应随时间变化的曲线，如图7，随后，再针对一阶波频和二阶低频运动根据1.3.2的介绍进行统计分析。

图7 漂浮方箱单弹簧约束时实测位移分离结果Fig. 7 Displacement separation results of floating box restrained by single spring

2.1 浮体固有频率

首先对顺应式浮体在静水中展开自由衰减试验研究，以方箱单弹簧连接结果为例。图8为漂浮方箱在单弹簧约束下纵荡方向的位移历时曲线。

图8 系泊浮体在静水中的自由纵荡衰减曲线Fig. 8 Free surge decay time history of moored floating body in still water

则漂浮方箱单弹簧约束下纵荡方向的固有周期为14.27 s，固有角频率为0.44 rad/s。同理，漂浮方箱双弹簧约束下纵荡方向的固有周期为9.91 s，固有角频率为0.63 rad/s；截断圆柱在双弹簧约束下纵荡方向的固有周期为12.62 s，固有角频率为0.50 rad/s。

2.2 系泊刚度对浮体慢漂运动的影响

随后分别对方箱结构在单弹簧连接和双弹簧约束时在不规则波作用下的慢漂运动展开试验研究。首先分析了不同弹簧刚度约束下漂浮方箱的一阶波频纵荡和升沉运动标准差，如图9所示。

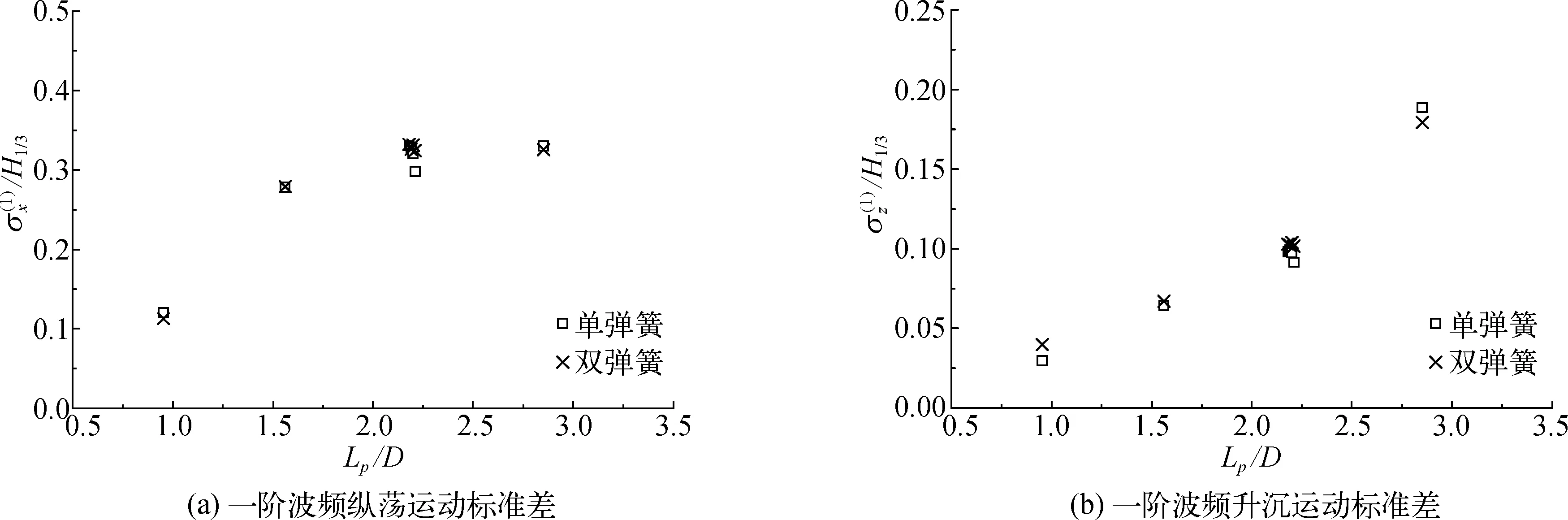
图9 漂浮方箱在单弹簧和双弹簧约束时一阶波频运动响应标准差对比Fig. 9 Comparisons of the standard deviations of the first-order motion response of the floating box at wave frequency under the constraints of single and double springs

图9中横坐标为谱峰波长比结构物尺寸，纵坐标为标准差比有效波高，用于描述不同谱峰周期不规则波作用下的一阶波频运动响应标准差，从结果可以看出漂浮方箱在单弹簧约束和双弹簧约束时，纵荡和垂荡方向无量纲化的一阶位移标准差基本相同，说明弹簧刚度对慢漂运动的一阶运动响应影响不大。这是因为在试验中方箱的固有周期与波浪谱峰周期相差很大，因此系泊的刚度对顺应式系泊浮体慢漂运动中的一阶波频运动响应影响不大。在纵荡方向，当谱峰波长为结构物尺寸的二倍以上，标准差不随着谱峰波长的增长而增长，而在垂荡方向则一直在增加。随后分析系泊刚度对二阶慢漂运动响应的影响，分别对二阶低频慢漂运动的平均漂移值和标准差进行分析，如图10和图11所示。图10为方箱分别在单弹簧连接和双弹簧约束时纵荡和垂荡方向二阶低频位移均值对比；图11为方箱在纵荡和垂荡方向二阶低频位移标准差对比。

图10 漂浮方箱在单弹簧和双弹簧约束时二阶低频运动响应均值对比Fig. 10 Comparisons of the mean values of the second-order motion response of the floating box at low frequency under the constraints of single and double springs

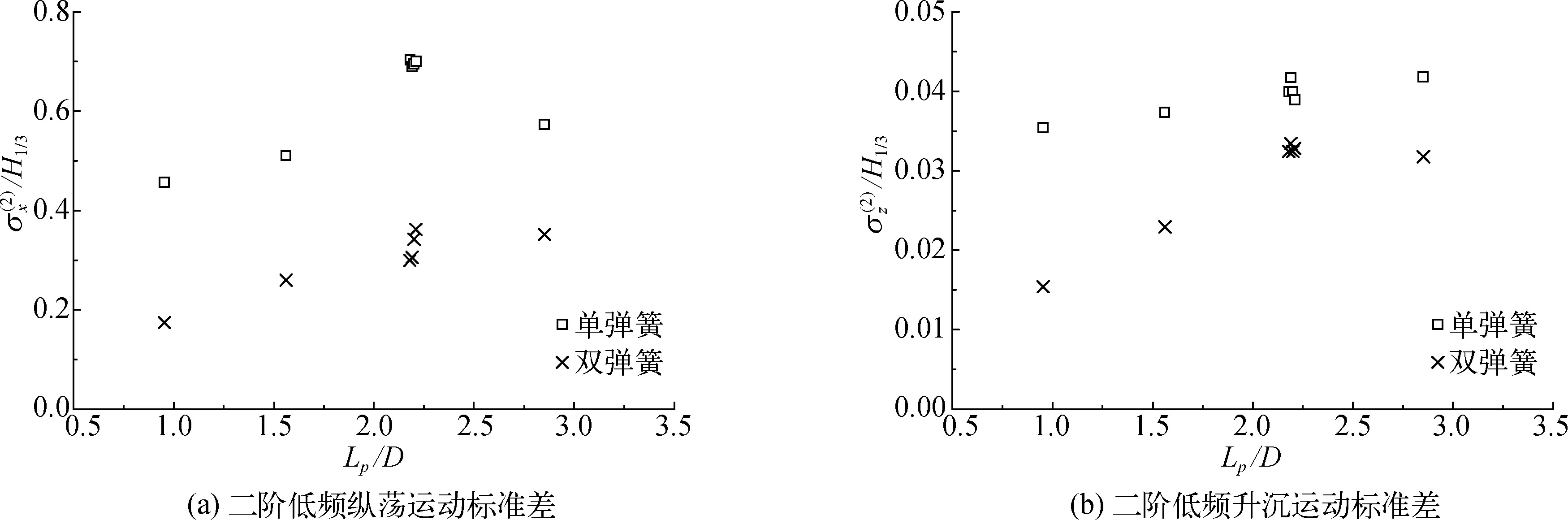
图11 漂浮方箱在单弹簧和双弹簧约束时二阶低频运动响应标准差对比Fig. 11 Comparisons of the standard deviations of the second-order motion response of the floating box at low frequency under the constraints of single and double springs

从图10和图11可以看出随着谱峰波长的增大，方箱的二阶漂移的均值也逐渐增大，说明不规则波的波长尺寸相对结构物尺寸越大，激发浮体的慢漂越远，而纵荡标准差同样在谱峰波长比结构物尺寸为2.0以上变化不明显，说明无论一阶还是二阶纵荡运动标准差，当谱峰波长为结构物尺寸2.0倍以上时，波浪对结构物纵荡运动幅度影响不大。同时发现系泊刚度对二阶低频慢漂运动响应影响很大，无论是平均值还是标准差。方箱在双弹簧约束下二阶低频运动都远小于单弹簧约束情况，均值和标准差仅为单弹簧约束下的40%到50%。而在垂荡方向由于并未施加弹簧约束，双弹簧约束下位移均值和标准差为单弹簧约束下的70%到80%。

2.3 浮体形状对浮体慢漂运动的影响

为了研究不同形状海洋工程对慢漂运动的影响，选择漂浮方箱和截断圆柱这两种应用最为广泛的形状在双弹簧约束下的慢漂运动展开试验研究。对比结果同2.2节，首先研究浮体形状对一阶波频运动响应的影响，随后研究了浮体形状对二阶慢漂运动的影响，结果同样进行了无量纲化处理，如图12至14所示。

图12 漂浮方箱和截断圆柱在双弹簧约束时一阶运动响应标准差对比Fig. 12 Comparisons of the standard deviations of the first-order motion response between the floating box and truncated cylinder at wave frequency under the constraints of double springs

从统计结果可以看出，漂浮方箱和截断圆柱在纵荡和升沉方向无量纲化的一阶位移有效值基本相同，说明浮体形状对浮体的一阶运动响应影响不大。其原因同样是顺应式漂浮结构的自振周期与波浪谱峰周期相差很大。而针对低频运动，从图13可以看出浮体形状对纵荡方向影响较大，截断圆柱的平均慢漂均值小于漂浮方箱，但是随着相对波长的增加两者的差距逐渐减小，升沉方向浮体形状对结果影响较小。从图14的标准差对比结果看，浮体形状对结果影响不大。

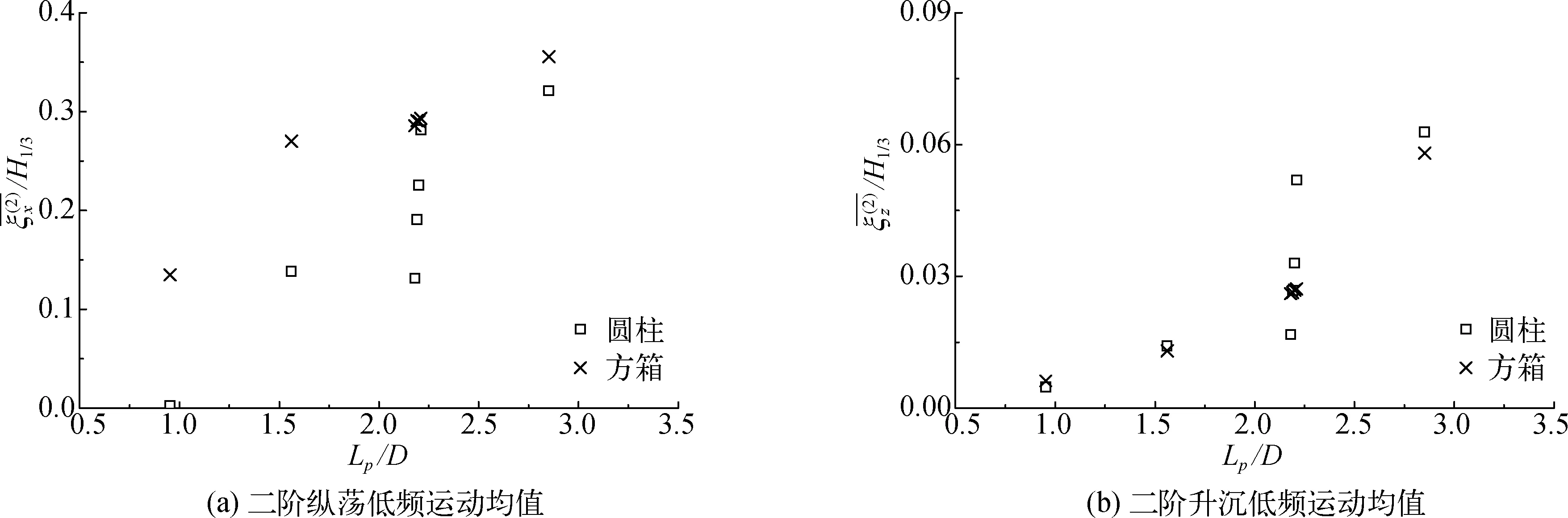
图13 漂浮方箱和截断圆柱在双弹簧约束时二阶低频运动响应均值对比Fig. 13 Comparisons of the mean values of the second-order motion response between the floating box and truncated cylinder at low frequency under the constraints of double springs

图14 漂浮方箱和截断圆柱在双弹簧约束时二阶低频运动响应标准差对比Fig. 14 Comparisons of the standard deviations of the second-order motion response between the floating box and truncated cylinder at low frequency under the constraints of double springs

3 结 语

通过物理模型试验对顺应式系泊浮体在波浪作用下的运动进行研究，分析了浮体系泊刚度和浮体形状对物体一阶波频和二阶低频运动响应的影响，研究结果表明:

1) 由于顺应式浮体的固有周期远离波浪谱峰周期时，系泊刚度以及浮体形状对慢漂运动的一阶运动响应影响不大；

2) 系泊刚度对慢漂运动的二阶低频运动响应影响较大，二阶低频运动相对偏离平衡位置的平均值和标准差均随系泊刚度增大而减小；

3) 浮体形状对慢漂运动的二阶低频运动响应纵荡方向的平均偏移值影响较大，升沉方向影响较小，对两个方向的标准差影响较小；

4) 当入射波浪谱峰波长为结构物尺寸2.0倍以上时，波浪对结构物一阶、二阶纵荡运动幅度影响不大。