高速铁路ω型扣件弹条的共振响应特征分析

2021-08-05姜秀杰李秋彤

铁道标准设计 2021年8期

姜秀杰,刘艳,2,李秋彤,2,赵威,刘欢

(1.上海材料研究所,上海 200437； 2.上海消能减震工程技术研究中心,上海 200437； 3.上海第二工业大学环境与材料工程学院,上海 201209)

扣件作为轨道结构中最重要的组成部件之一，为车辆运行安全性和平稳性提供保障。扣件系统中的弹条元件在服役过程中承受弯扭组合交变应力作用，当线路不平顺较严重时，可能导致弹条局部区域发生过载现象，从而过早地发生疲劳断裂，威胁行车安全。

近年来，国内外学者针对弹条断裂原因做了多方面研究。潘兵等[1]通过现场测试和仿真计算得出饱和的轮轨系统纵向蠕滑力会激起轮轨系统在500 Hz和600 Hz附近的不稳定振动，从而引发弹条共振，造成弹条损伤。侯尧花等[2]基于声振互易法对WJ-8扣件弹条进行了频响函数和现场模态测试，准确获取了弹条组装状态下的模态特征。肖宏等[3]分析了e型弹条在自然状态和服役状态下的模态振型及频响特性，提出可通过降低车速来提高弹条的服役时间。THOMPSON D.J等[4]研究了5种不同扣件系统的动力性能，分析得出荷载频率对扣件系统刚度的影响规律。SUN Linlin等[5]以Vossloh 300-1扣件系统为研究对象，比较了弹条模态特征测试方法对弹条固有频率的影响。LIN Liang等[6]通过计算得出钢轨表面的短波波磨是导致扣件失效的最主要原因，这种类型的波磨可引起轨道系统在700～1 000 Hz内存在明显的共振峰。周华龙等[7]通过测试频断地段III型弹条的固有频率以及现场轨道的动态位移和加速度，得出高频高幅值的振动强度以及高频激振力诱发的弹条共振会大大降低弹条的寿命。刘慧娟[8]利用模态和频响理论对服役状态下的弹条进行振动特性分析，得出扣件系统共振是引发弹条断裂的重要原因。朱胜阳等[9]研究了弹条在安装过程中的受力及列车动荷载作用下的振动特性，得出当钢轨存在波磨时，弹条振动加速度比没有波磨相比增大10倍，会加速弹条的疲劳损伤。黄浩志等[10]对结构空心改进后的W1弹条进行了组装模态仿真，为提高弹条固有模态频率提供了可行方案。邓士豪等[11]计算了弹条模态频率随约束刚度的变化规律，结果表明弹条不同部位以及不同方向的约束刚度对模态频率和共振峰幅值均有显著影响。

综上分析可知，多数研究得出钢轨波磨引起的扣件系统共振是弹条断裂的主要原因之一，但少有学者对弹条共振后的时域和频域力学行为进行分析。且既有研究大多采用加速度传感器或声振互易法，结合仿真手段，获取弹条的模态特征。但是对几何形状和边界条件都十分复杂的弹条，此类测试方法很难掌握包含模态振型在内的弹条完整模态信息。因此，本文基于仿真分析，结合数字图像相关(DIC)技术，对自由和组装状态下的扣件弹条进行模态特征研究，并对外力激励下产生共振的弹条元件进行力学行为分析，进一步揭示弹条过早发生疲劳断裂的机理和诱因。

1 组装扣件系统有限元模型

1.1 模型构成和网格属性

按照组装扣件系统实物尺寸及图纸建立有限元模型，模型包含钢轨、绝缘垫片、螺栓、螺栓垫片、弹条、轨距挡板、轨下垫板、铁垫板、弹性垫板和轨枕在内的10个元件，如图1所示。为保证计算精度同时节约计算成本，模型中的弹条和轨距挡板采用10节点四面体单元；钢轨、螺栓、螺栓垫片、绝缘垫片、轨枕和铁垫板采用8节点线性单元；轨下垫板和弹性垫板采用20节点二次单元，详见图2(a)。弹条各局部区域命名方式如图2(b)所示。

图1 ω型扣件模型

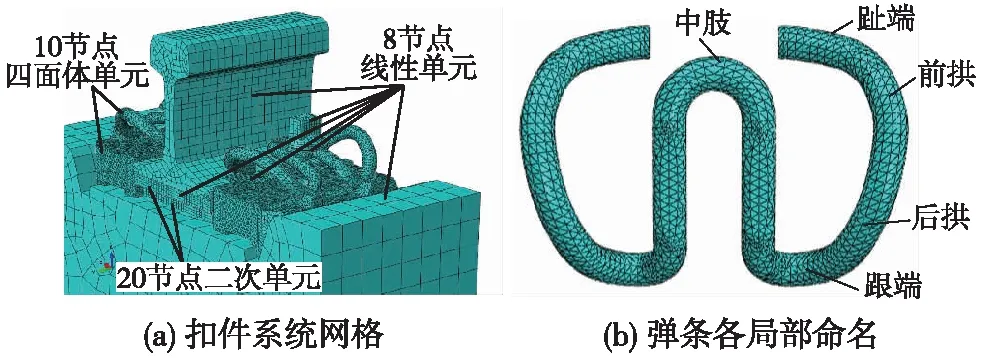
图2 弹条扣件网格划分

1.2 材料属性

扣件系统中各部件材料属性如表1所示，其中弹条元件考虑弹塑性特性，采用实际拉伸试验获取的完整应力-应变曲线定义，曲线特征参见图3[11-13]。

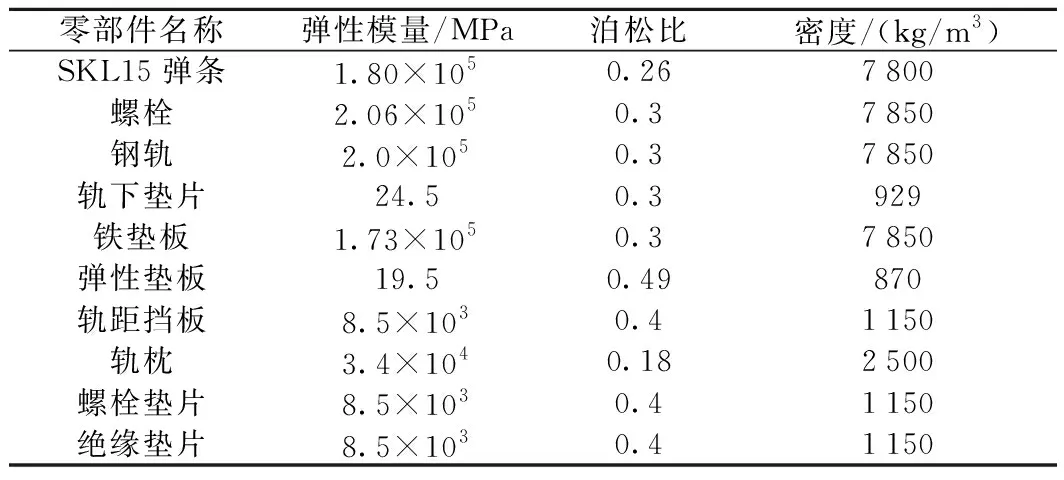
表1 扣件系统各部件材料属性

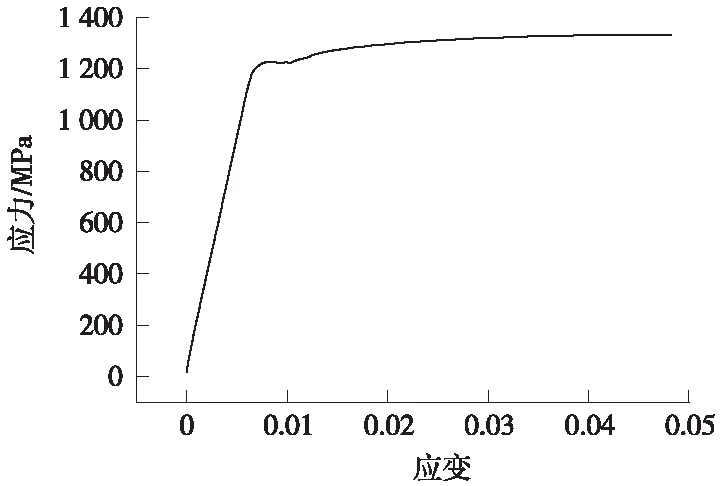
图3 弹条材料拉伸曲线

1.3 接触及约束属性

采用点-面非线性接触处理弹条与其相接触元件间的接触关系，法向接触采用硬接触，两物体间不允许穿透，切向接触采用库伦摩擦模型[14-15]。其余元件间均采用无摩擦的绑定约束，约束弹条中肢y方向的自由度。在螺栓上施加相应的预紧力F，如图4所示，达到与标准扭力矩250 N·m相同的钢轨扣压力，此时，整个扣件系统达到标准安装状态。

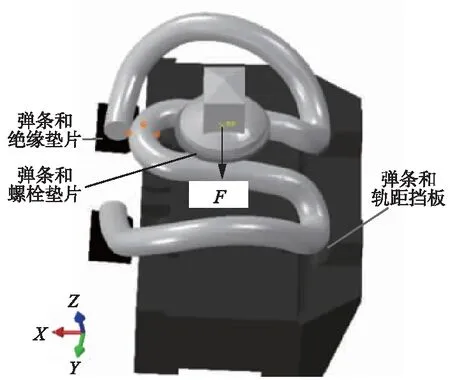
图4 弹条接触及约束属性

2 模态计算及分析

2.1 自由模态仿真分析

单独对弹条元件进行自由模态分析，考虑弹条在0～1 000 Hz频率范围内的自由模态[5-6]。SKL15弹条前5阶振型及固有频率如图5所示，具体振型特点归纳总结至表2。

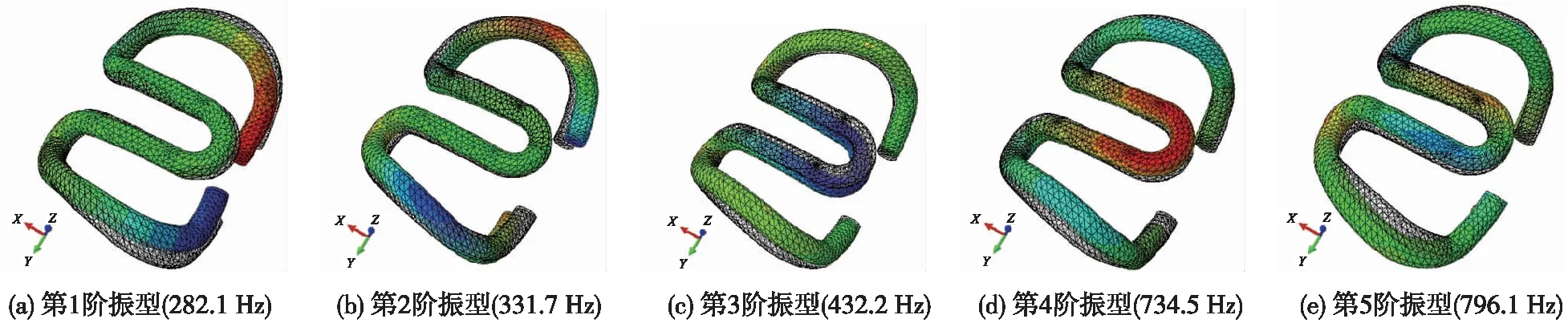
图5 弹条自由模态振型和频率

图5中，透明网格和彩色网格分别代表弹条未变形和变形后的空间位置。

由表2中所描述的各阶振型特点可知，第1阶模态振型为弹条趾端和前拱沿y轴对称运动，跟端处于压缩状态，第2、3、4、5阶模态振型均为弹条趾端和左右两拱相对跟端沿z轴呈同相位或反相位的运动，跟端处于弯扭组合变形状态。

多元积分学是高等数学的主要内容之一，而三重积分的计算是其重点和难点。教学实践中，从教学反馈和考试情况来看，学生往往反映难度很大，特别是在将三重积分转化为累次积分时，很难顺利地确定累次积分的积分上限和积分下限；主要原因在于没有真正理解教材中的投影法和截面法。而一般教材和已有文献多是简单地介绍在直角坐标下三重积分的投影法和截面法，[2]介绍了在柱面坐标下的一个投影法，即将积分区域投影到极坐标面上，将三重积分转化为先一后二的积分，再将外层的二重积分转化为二次积分，最终实现将三重积分转化为三次积分。然而，柱面坐标下三重积分的投影法还不够完善。

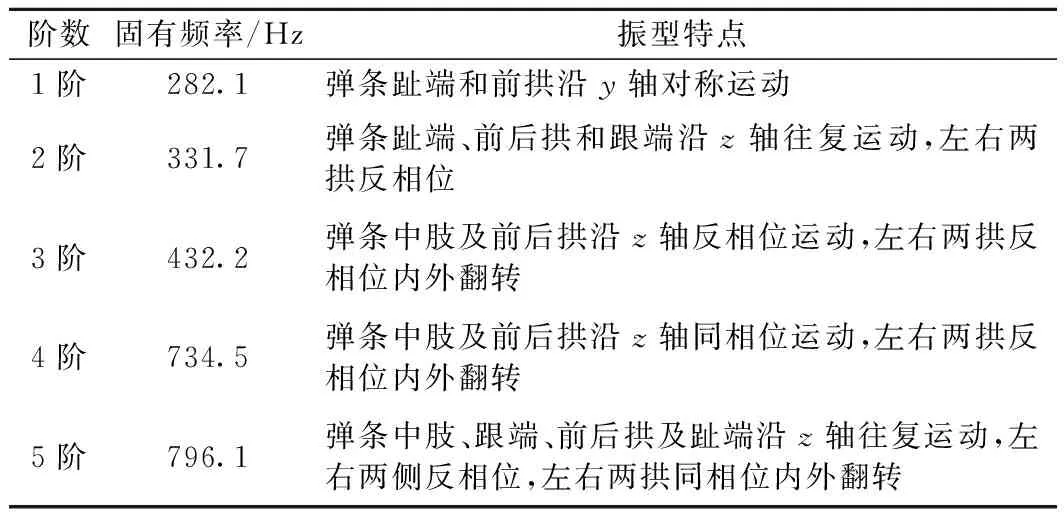
表2 弹条自由模态固有频率及振型特点

2.2 组装模态仿真分析

进一步计算分析弹条在标准安装状态下的模态振型及频率特点，同样考虑1 000 Hz以内的模态特征。计算结果如图6所示，0～1 000 Hz内弹条存在两阶组装模态，具体振型特点如表3所示。

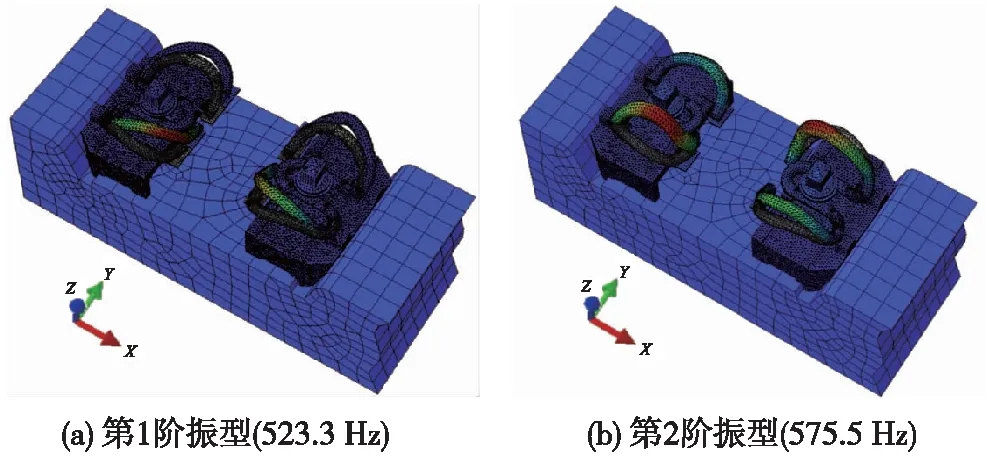
图6 弹条组装模态振型和频率

表3 弹条组装模态固有频率及振型特点

图6中，弹条元件的透明网格和彩色网格同样代表未变形和变形后的空间位置。由表3所描述的各阶振型特点可知，弹条前两阶组装模态振型主要表现为其左右两拱相对于趾端及跟端的反相位交替或同相位往复运动，弹条跟端小圆弧区域处于典型的弯扭组合变形状态。

3 模态试验及仿真对比分析

3.1 模态试验过程

为验证有限元模型的准确性，以便进一步分析弹条的共振响应特征，基于数字图像相关(DIC)技术，采用2台Photron FASTCAM SA-X2-1000k高速相机(内存72 GB，分辨率为1 024×1 024像素)，对ω型扣件系统中的弹条元件进行自由模态和组装模态测试[16]。其中，系统测量精度会受采样频率的影响，采样频率越高，测量精度越高。本文测试过程中将采样频率设置为12 500 Hz，此时位移测量精度为40 nm，满足弹条模态测试要求。

试验前，首先采用黑白哑光喷漆，在弹条表面制作具有高灰阶差异的人工散斑；然后将2台高速相机架设在预定位置，根据试验环境调整光源，用标定板标定测量系统。试验时，用小锤多次重复敲击弹条不同部位，采集弹条变形前后的散斑图像。试验后，将图像文件输入至后处理系统，设置子区搜索参数，采用数字图像相关算法对2台相机采集到的图像信息进行匹配，得到被测表面的全场位移信息，实现非接触式全场变形测量[17-19]。

在弹条自由模态测试中，为消除边界影响，将弹条放置在海绵上。高速摄像机架设在弹条斜上方，锤击弹条不同部位使其充分响应，分析并总结归纳可重复获得的模态信息，自由模态测试见图7。

图7 弹条自由模态测试

在弹条组装模态测试中，使用数显扳手对弹条施加250 N·m的扭矩将其达到标准安装状态，高速摄像机的架设角度、调试过程以及锤击方法与自由模态测试保持一致，组装模态测试见图8。

图8 弹条组装模态测试

3.2 自由模态试验结果

试验获取弹条各阶自由模态振型和频率，详见图9。对比图5和图9可知，数值模拟与试验获得的弹条各阶自由模态振型一一对应，具备较好的一致性，且各阶模态频率最大仅相差2.3%。由此，验证了弹条几何尺寸、材料属性和计算过程的可靠性。

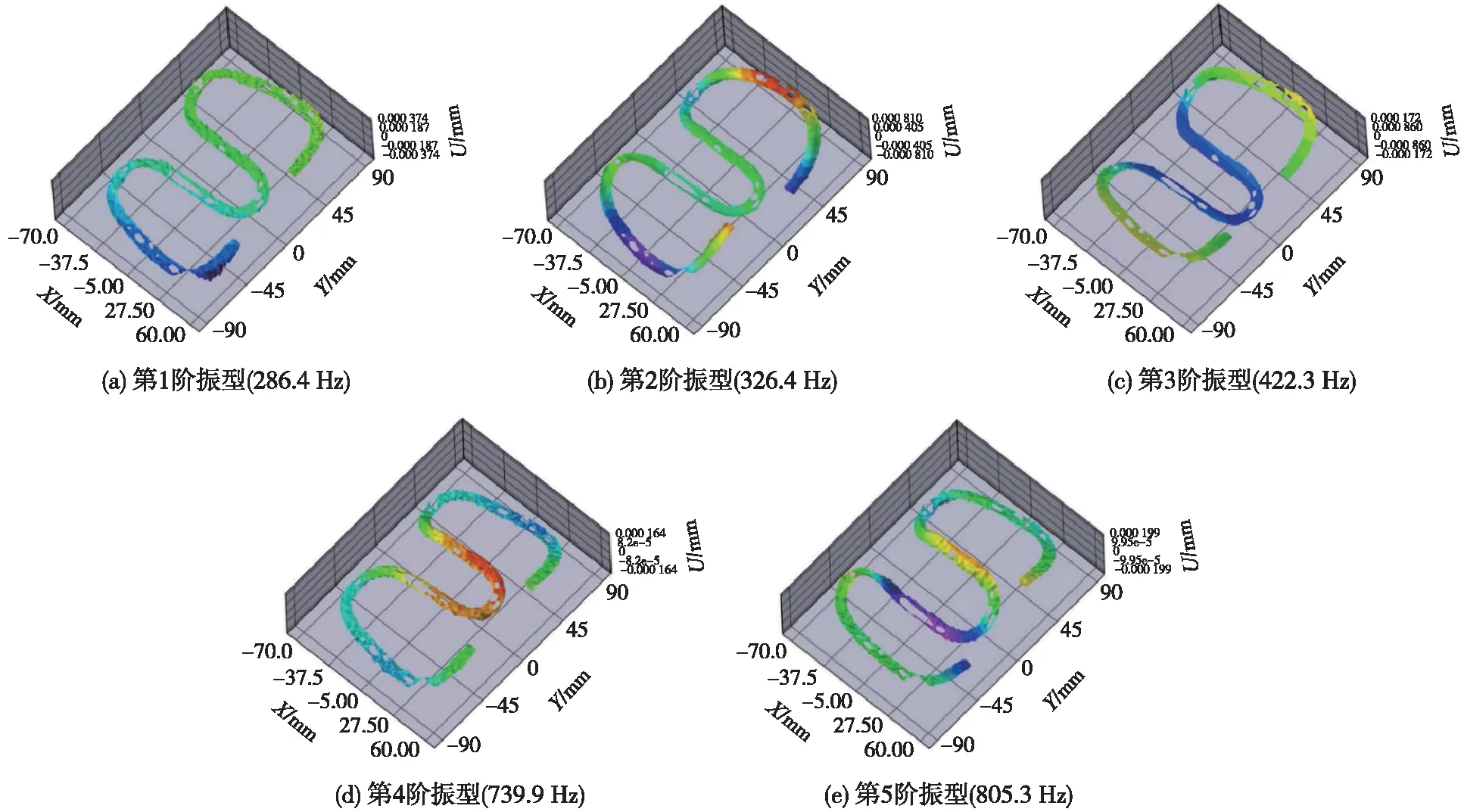
图9 弹条自由模态振型和频率

3.3 组装模态试验结果

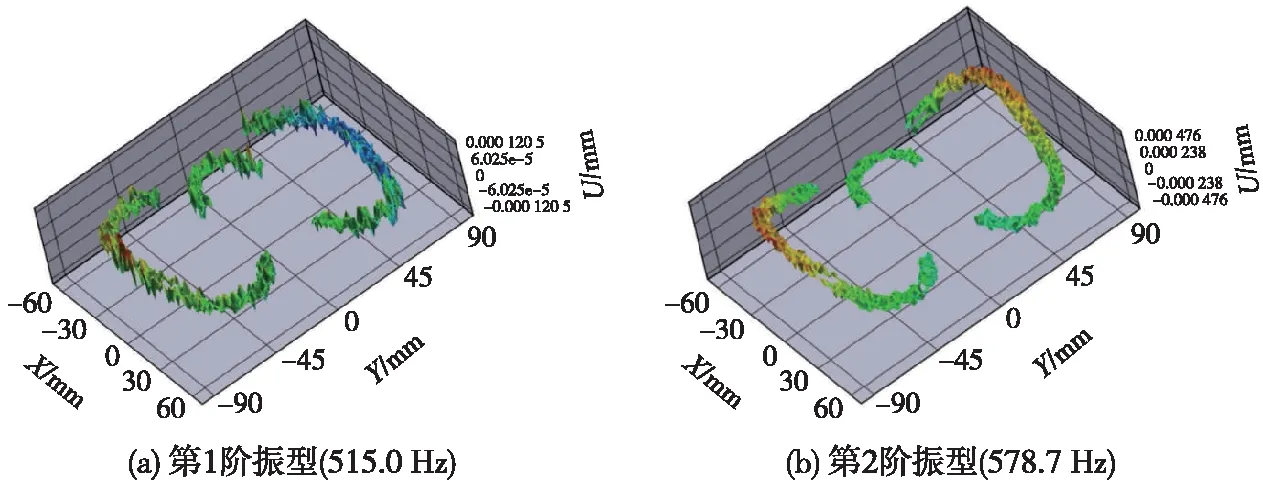
图10 弹条组装模态振型和频率

4 频响分析

利用已通过试验验证的仿真模型，进一步对组装扣件系统进行频响分析。在图2(a)所示钢轨轨头表面施加垂直向下的单位正弦荷载，扫频频率范围为0～1 000 Hz，计算并拾取弹条趾端及两拱最高点位置处的位移和加速度响应，结果如图11所示。

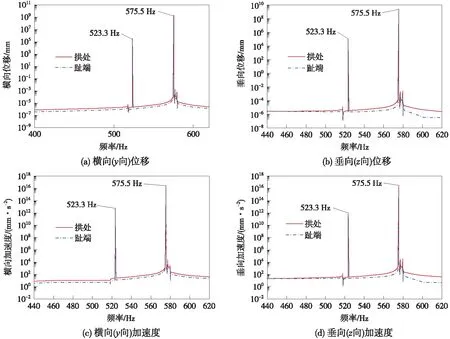
图11 弹条加速度和位移响应

由图11可知，弹条趾端和两拱最高点处的垂、横向位移及加速度响应均存在两个全局峰值，频率分别为523.3 Hz和575.5 Hz，与弹条的前两阶组装模态频率接近。图12为频响分析过程中，弹条在不同频率荷载激励下的等效应力云图。其中，图12(a～b)为非共振频率的低频和高频荷载激励下的等效应力云图，图12(c～d)的荷载频率对应图11中的两个全局峰值，即共振频率荷载激励下的等效应力云图。对比4张云图中的最大等效应力值可发现，当扣件系统所受荷载的频率与弹条组装模态固有频率接近或一致时，弹条跟端应力显著放大，远大于非共振频率荷载激励时的应力响应值。此外，可明显看出图12(d)中弹条等效应力值远大于图12(c)，这是因为弹条1阶组装模态振型主要表现为趾端和前拱沿y向的往复运动，而2阶组装模态振型主要表现为两拱沿z向的往复运动，后者更易于引发弹条跟端小圆弧区域的弯扭组合变形，导致等效应力值更大。

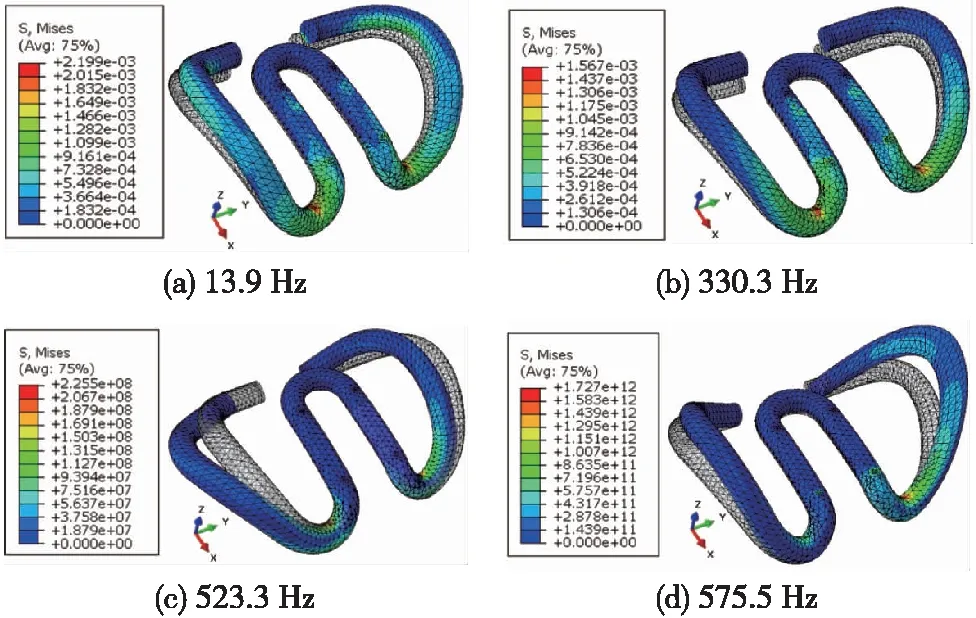
图12 不同频率荷载激励下弹条等效应力云图

5 路谱激励下弹条时频响应分析

计算路谱激励下的弹条振动响应，常采用自由短轨和单组扣件系统的有限元模型求解[13，20-21]。因此，本文基于经充分验证的有限元仿真模型，进一步对弹条在行车荷载作用下的共振响应特征进行仿真分析。在钢轨轨头施加我国某高速铁路实测路谱，如图13中黑色实线所示(工况Ⅰ)。在此基础上，分别叠加弹条的前两阶组装模态频率523 Hz(工况Ⅱ)和575 Hz(工况Ⅲ)，表征有波磨存在的轮轨，叠加生成的时域和频域荷载谱详见图13中的红色虚线和蓝色点线，所叠加的共振频率成分幅值参照相关文献设置[22]。获取弹条拱处在含有波磨路谱激励下的加速度时域响应，并与某高速铁路实测结果对比，如图14所示。由图14可知，弹条振动加速度的仿真与实测结果在形态和幅值上均具有较好的一致性[20]。由此可以表明，虽然所用模型为短轨与单组扣件系统，与钢轨实际受力条件不符，但钢轨的约束状态对行车荷载作用下的弹条振动特性影响较小，对计算结果准确性的影响甚微，可忽略不计。故本文建立的有限元模型，可有效分析轨道荷载谱影响下的弹条振动响应。

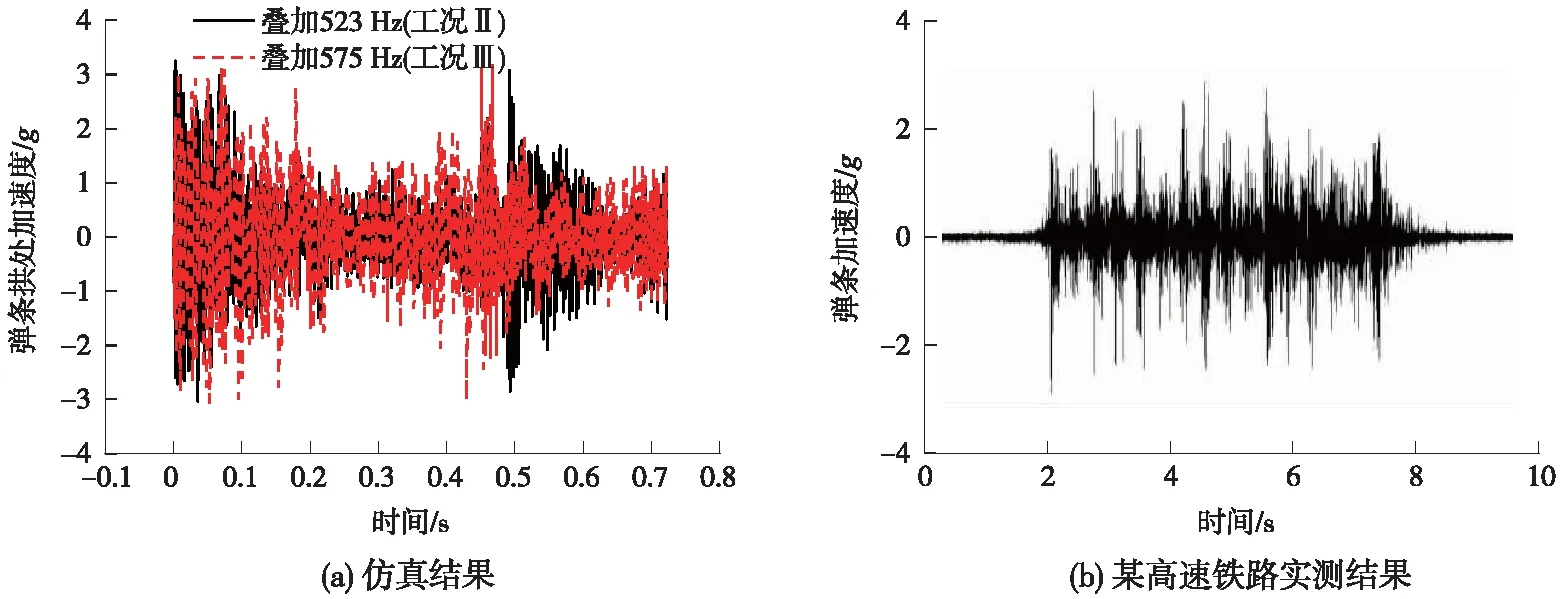
图14 路谱激励下弹条加速度时域响应仿真与实测结果对比

在3种轮轨荷载谱作用下，计算拾取弹条两拱最高点位置的垂向位移和加速度响应以及弹条跟端等效应力，傅里叶变换得到的频域响应特征如图15所示。

图15 弹条频域振动响应

由图15可知，在3种荷载激励工况下，弹条两拱垂向位移及跟端等效应力的全局最大值均发生在30 Hz以下的低频范围，该部分响应是行车荷载作用下的强迫振动响应。

在207 Hz频率附近范围内，弹条两拱位移、加速度以及跟端等效应力均存在局部峰值，由前文中扣件系统组装模态和频响分析结果可知，该频率为组装扣件系统的第4阶固有频率，模态振型表现为钢轨沿z轴的垂向振动，弹性垫板被周期性地弹性压缩和释放，进而带动弹条趾端及前拱产生变形。但该阶振型与图6及图10所示的弹条组装模态振型有所区别：前者表现为弹性垫板的局部变形导致钢轨振动，由于弹条对钢轨始终保持扣压状态，因而进一步带动弹条变形；而后者则表现为弹条元件独立的振动变形。组装扣件系统的前3阶模态响应同样是由于橡胶垫板的弹性变形引起的，振型分别表现为钢轨绕z轴转动，以及沿x轴和y轴的平动，但这3阶振型对弹条元件，尤其对弹条跟端的应力响应影响较小。此外，由图15还可看出，工况Ⅰ、工况Ⅱ和工况Ⅲ中弹条两拱位移及加速度响应在364 Hz附近区域内也存在小幅值的局部峰值。根据前文计算可知，该频率为组装扣件系统的第5阶固有频率，模态振型表现为扣件系统中的铁垫板相对于钢轨和轨枕沿z轴转动。铁垫板转动过程中，钢轨沿对角线方向发生偏心振动，从而带动弹条趾端和两拱产生小幅度的内外翻转。

相比于工况Ⅰ，图15(a～c)中红色虚线和蓝色点线所示的工况Ⅱ及工况Ⅲ，还分别激励起了所叠加频率成分的振动响应，即弹条元件的组装模态频率523 Hz和575 Hz，弹条两拱位移、加速度及跟端等效应力均在相应频率处产生了较窄带宽的共振放大现象。需进一步说明的是：工况II还引起了307 Hz频率成分的振动放大现象；工况Ⅲ激励起了254 Hz的频率成分响应。通过对这两阶频率及对应振型分析可知，这两阶频率分别与弹条元件自由模态的二阶和一阶固有频率相近；弹条元件二阶自由模态振型与其一阶组装模态振型在趾端区域沿y向振型相似，弹条元件一阶自由模态振型与其二阶组装模态振型在前拱区域沿y向振型相似。可见，在包含弹条高阶敏感频率成分的行车荷载作用下(工况Ⅱ和工况Ⅲ)，弹条的工作变形(ODS)表现为组装模态和自由模态的叠加，从而导致弹条的工作振型响应比没有叠加高频敏感频率时(工况Ⅰ)更加复杂，振动幅度增大，致使弹条跟端区域更易于发生因局部过载导致的疲劳破坏。