计及网络重构的主动配电网供电能力概率评估

李沛然，袁旭峰，赵 真，简 力，熊 炜，邹晓松

（贵州大学 电气工程学院，贵州 贵阳 550025）

0 引言

供电能力是反映配电网安全性和经济性的重要指标，指满足一系列约束条件下配电网可以输送的最大功率，主动配电网（active distribution network，ADN）由于其主动控制特性和分布式电源（distributed generation，DG）的加入使供电能力的评估方式和尺度发生了变化，因此准确评估主动配电网的供电能力就成为急需解决的问题。

主动配电网相比于传统配电网的一个优势在于可采取对系统中“源–荷–网–储”协同控制方式[1]。主动配电网对配电网资源的主动决策管理和控制，通过对各元素的控制和网端灵活重构，实现电网高质量运行。近几年也有一些文献对含DG的配电网供电能力进行研究。文献[2]改进了重复潮流法，求取各种方案下网络每小时的供电能力，建立了一系列指标，并用德尔菲法综合评估各项指标，但该文献的风光出力以及评估权重过于单一。文献[3]通过对风光出力的不确定性构造盲数模型，实现含DG的供电能力评估，但对于风光的盲数设置缺乏实际的支持。文献[4]提出一种多目标直流配电网供电能力模型，利用智能算法对不同接线形式下的风光接入情况下的供电能力进行求解，研究了渗透率与供电能力的相关性。文献[5]针对风光出力以及线路故障的随机性生成场景，对主动配电网短期的供电能力进行评估。文献[6]运用两点估计法计算含DG配电网的最大供电能力分布，得出全局和不同区域下的供电能力分布函数。文献[7]模拟了 DG及负荷的变化过程，并以此为依据进行供电能力的评估。文献[8]在安全性的基础上又考虑了用户的需求，在双重约束下评估配电网的供电能力。文献[9]通过半不变量法处理DG的不确定性，对含DG的配电网进行供电能力评估。

以上文献对主动配电网的供电能力进行了一定程度的研究，但只在单一的运行方式下评估配电网供电能力的结果偏向保守，不符合主动配电网的主动控制特性和发展趋势[10-15]。因此主动配电网供电能力的评估需要以网络重构为基础，通过重构优化得到最有利于主动配电网供电能力的网架结构[16]。针对电网的随机性，本文建立了新的供电能力评价指标体系，选择适合评估供电能力的概率潮流计算方法，重点分析 DG接入前后与不同运行方式下配电网供电能力产生差异的原因，并以供电能力的期望为目标函数找到主动配电网最大的供电能力运行方式，为主动配电网的日常运行提供参考。

1 ADN供电能力评估指标

本文将主动配电网供电能力定义为在满足约束条件的前提下，网络能携带最大负载的能力PNSC（network supply capacity，NSC），目标函数如式（1）[17]：

式中：PNSC表示满足约束条件下主动配电网的供电能力；Ppi表示i节点的初始负荷；Pni表示i节点基准负荷；k表示i节点基准负荷的增长倍数，n表示网络节点数。

PNSC求解过程如下：所有节点的基础负荷值按照一定比例不断增长，如果负荷越限则返回前一次数值，减小k的数值继续让负荷增长，最终达到最大值。本文将k达到最大值时的PNSC作为电网供电能力。

由于DG出力的不确定性，配电网供电能力不再是一个确定性的值，下面利用一系列新的指标来评价主动配电网的供电能力。

（1）供电能力期望ENSC

反映DG随机出力的情况下配电网能达到的平均供电功率，供电能力期望ENSC可表示为：

式中：N表示蒙特卡罗随机抽样次数；PiNSC表示第i次抽样所对应的供电功率。

（2）供电能力标准差Dz

该指标表示的是抽样下每个PNSC的均匀程度，具体公式表示如下：

（3）供电能力峰值Pmax

该值指的是经过N次抽样后样本中能输送的最大供电功率，由统计学规律可知如果样本在[ENSC–3Dz,ENSC+3Dz]区间内，样本的覆盖率为99.7%，故可以将样本中供电能力峰值定义如下[18]：

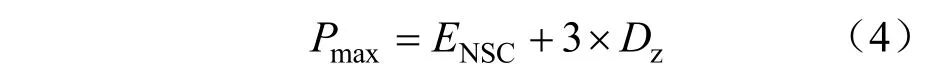
（4）供电能力谷值Pmin

该值指的是经过N次抽样后样本中能输送的最小供电功率：

（5）变异系数c

变异系数，用来比较均值显著不同样本之间的离散状态，具体计算公式如下：

（6）供电裕度η

供电裕度反映的是主动配电网除开当前负荷后携带负荷的能力，公式如下：

2 ADN供电能力概率评估

2.1 DG及负荷数学模型

由于主动配电网中 DG出力及负荷波动具有不确定性，分别用概率分布函数模拟各元素[19-20]。

风速服从Weibull分布，公式如下：

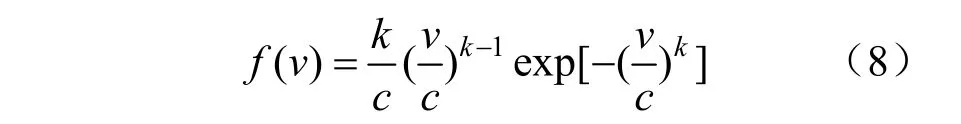
式中：k和c表示形状和尺度参数。

风速是风机出力的决定性因素，风力发电的功率与风速的具体函数如下所示：

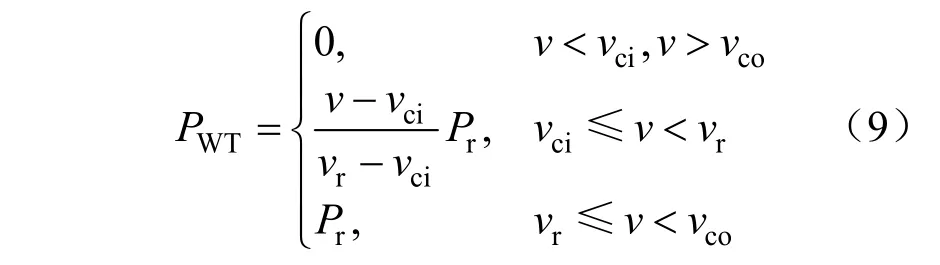
式中：vci和vco为切入、切出风速，vr和v分别为额定与实际风速，Pr和PWT为风机额定功率、输出功率。

光伏出力符合Beta分布，公式如下：

α2和β2表达式如下：

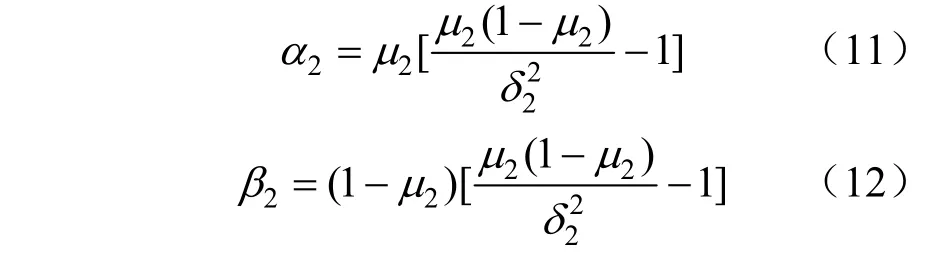
式中：μ2和σ2为光照强度均值标准差。

考虑到主动配电网中存在大量可中断负荷和可转移负荷，设负荷服从正态分布N(PN,σ)。PN和σ为均值及标准差[21]。

2.2 ADN供电能力概率评估

若评估对象为含有k个随机变量的主动配电网，每个随机变量需要估计出3个样本点进行计算，根据概率统计理论，配电网中所有DG以及负荷构造的样本点离散分布的前k阶矩与待求随机变量的前k阶矩相等，通过对离散点前k阶矩求解，计算出概率密度函数。构造配电网中每个随机变量对应的样本点，每个分量的计算方式如下：

式中：μk是X的一阶原点矩；σk是xk的标准差；xk,1，xk,2，xk,3分别是X的第k个随机变量估计点；ξk,1，ξk,2，ξk,3是每个样本点对应的位置参数。

样本点权重与位置参数的关系如下：

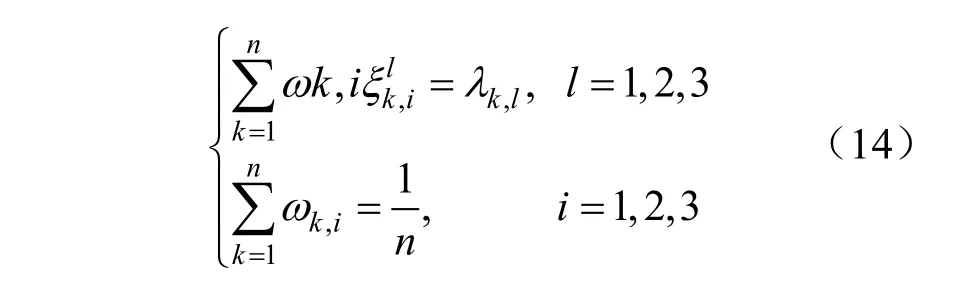
式中：λk,l表示l阶中心距Ml(xk)与σk的l次方的比值，即：

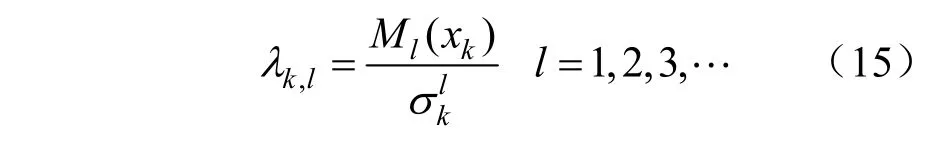
式子中λl,l=0；λ2,l=1；λ3,l为xk的偏度，表示的是相对于正态分布该分布函数的偏差；λ4,l为xk的峰度，表示的是分布函数在平均值附近的斜率情况。

配电网中含有的随机变量可以利用点估计法通过式（12）的3个样本点及其对应的位置参数与权重转化为确定性计算。

约束条件具体公式如下所示：

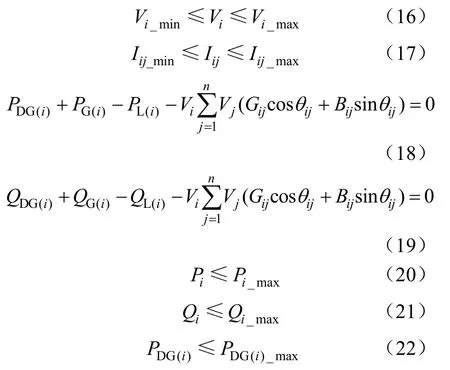
式中：Vi表示i节点电压；Iij表示支路电流；Vi_min、Vi_max、Iij_min、Iij_max分别为其约束上下限。PG(i)和QG(i)表示i节点发出有功、无功；PL(i)和QL(i)表示i节点有功、无功负荷；Gij、Bij、θij分别表示i与j间的电导、电纳、相角；Pi和Qi表示i节点变压器有功、无功容量；Pi_max和Qi_max为其上限。PDG(i)表示i节点DG发出功率，PDG(i)max为其输出功率上限。

最大功率分布具体计算流程如图1所示：

图1 主动配电网供电能力概率评估流程图Fig. 1 Flow chart of probabilistic evaluation of power supply capacity of active distribution network

步骤1：输入电网的原始参数，给定各个节点的初始基准负荷有功Ppi，若含有n个随机变量，运用三点估计法分别取出3n个样本进行计算。

步骤2：设定每个节点的增长有功负荷Pni以及负荷增长步长k，同时给定计算精度e。

步骤3：增大负荷带入网络计算，判断是否满足约束条件，若不满足进行步骤4，若满足继续增大负荷。

步骤4：用P=Ppi–kPni作为下一次潮流计算的各节点实际负荷。

步骤5：判断k是否比计算精度小，若k大于e，实施步骤6，若k小于e，实施步骤7。

步骤6：缩短步长k，让负荷的增长步长从k变为k=k/2返回步骤5，若不满足计算精度，则先令P=Ppi–kPni，需要返回步骤3继续迭代。

步骤7：计算结束后得出每个随机变量对应的3个样本点的供电功率，并利用式（14）求出供电功率的统计特征值λi,l。

根据半不变量的数学性质，可以计算出供电能力统计量的前t阶原点矩，公式如下：

式中：γt+1表示t+1 阶半不变量，t=1,2,…

利用 Cornish-Fisher展开公式求取随机变量的概率密度y(φ)，φ为供电功率y分位数，近似表示为：

式中：ξ(φ)=Ф–1(φ)，Ф表示标准正态分布N（0,1）

利用y(φ)=F–1(φ) 的性质，可以计算出供电能力y的概率分布函数F(φ)。

按照上述流程，首先根据各随机变量的中心矩，计算出估计点的位置参数及相应权重，根据计算后的值，利用重复潮流法求出网络供电能力的样本值和各阶矩，采用Cornish-Fisher级数将计算出的供电能力样本值和各阶中心矩展开，求出供电能力的分布和概率密度函数。

3 计及配网重构的主动配电网供电能力优化

3.1 目标函数与约束条件

目标函数设为ADN中供电能力期望最大，具体表述如下式：

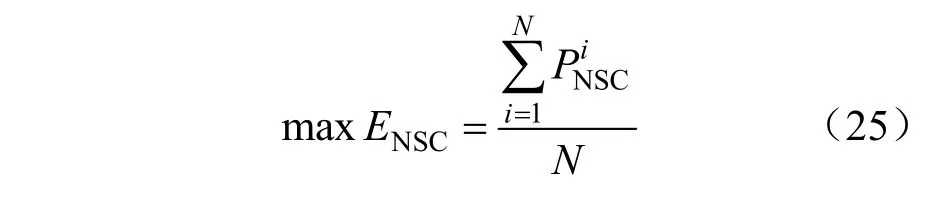
约束条件除了式（15）～（20）中的网络约束外，考虑DG出力的随机性约束条件式（21）改为下式[22]：

式中：α为预设的置信度，设定为0.95。

此外还需考虑配电网的网络结构约束，保障配电网辐射状运行，公式如下：

式中：i,j表示节点编号；V表示网络节点集合；n表示配电网节点数。

3.2 求解方法

本文运用二进制粒子群算法（binary particle swarm optimization，BPSO）计算配网重构，提升配电网的供电能力[23]。二进制粒子群算法更新速度和粒子位置可以用下式表示：

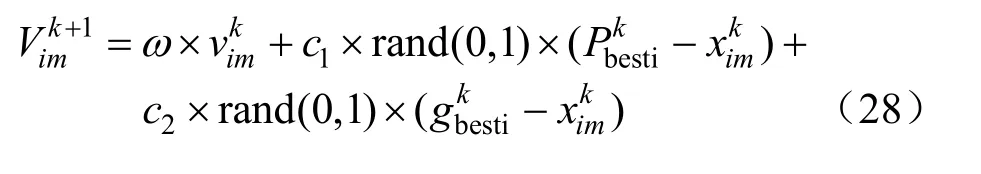
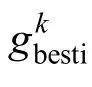
式中：ρ表示在[0,1]内产生的随机数。

sigmoid函数表述如下：

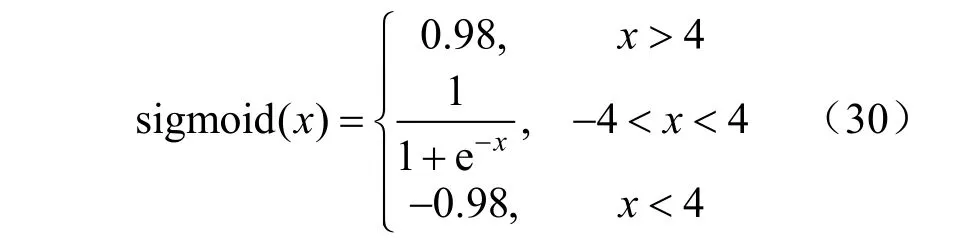
通过不断调整搜索过程中ω的值，使开始计算时搜索的解空间较大，算法后期可以缩小区域精准搜索加快收敛，更新权重ω的公式如下：

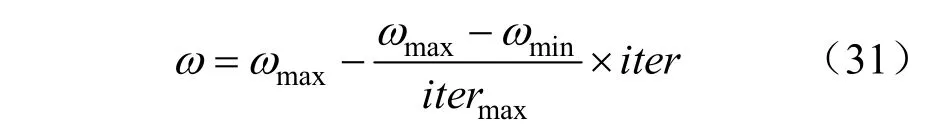
式中：ω表示权重系数，ωmax和ωmin分别是其最大最小值；iter表示当前迭代次数，itermax表示迭代次数上限。

基于配网重构的供电能力评估具体的求解流程如图2所示。

图2 基于BPSO的供电能力配网重构流程图Fig. 2 Flow chart of reconfiguration for power supply capacity distribution network based on BPSO

具体计算步骤如下：

步骤1：输入种群数目，最大迭代次数，电网的初始数据，网络开关的开断信息，以及控制变量的个数。

步骤2：根据初始的开关状态，确定当前的运行方式，利用上一节计算方法得到当前供电能力的分布函数期望值，计算粒子适应度。

步骤3：计算出粒子的全局最优位置，更新开关状态后，计算当前运行方式是否满足一系列约束条件。

步骤4：若满足约束条件则形成新的网络拓扑结构，若不满足回到步骤3。

步骤5：计算新网络下的供电能力期望值，得到适应度函数，并保留最大值。

步骤6：判断是否达到迭代上限，若达到输出结果，若没有返回步骤3。

步骤7：计算结束，输出优化后的配电网拓扑结构与对应的供电能力分布。

4 算例分析

4.1 算例模型

算例模型选取PG & E69节点配电网，如图3所示，电网初始负荷为4.38+j2.1 MVA，在电网节点33、37、52处加入风电，最大出力400 kW，在25、67、41处加入光伏，最大出力300 kW，风电和光伏的控制策略采取恒功率因数方式运行[24-25]。DG参数见表1、表2。

图3 算例模型Fig. 3 Example model

表1 风机参数Tab. 1 Fan parameters

表2 光伏发电的相关参数Tab. 2 Relevant parameters of photovoltaic power generation

4.2 算例1

算例1直接计算原始网络的供电功率分布，采用三点估计法（three point estimation method，3PEM）与蒙特卡洛法（monte carlo solution，MCS）（n=1 000）进行对比[26]。计算结果如表3所示：

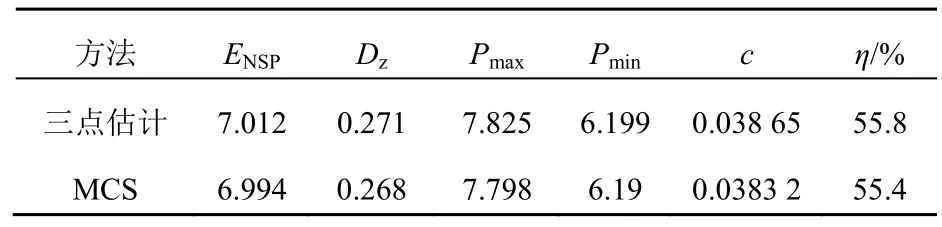
表3 算例1下配电网供电能力指标（MW）Tab. 3 Power supply capacity index of distribution network under example 1

从结果来看 MCS与本文所用三点估计法计算出的供电能力的分布函数重合度较高，MCS计算得出的ENSP为7.012 MW标准差为0.271，三点估计法计算得出的ENSP为6.994 MW，标准差为0.268，验证了本文所提方法能够有效地计算出主动配电网供电功率的分布函数。同时由于重构前负荷分布不均匀，故而电网的供电裕度只有55.8%，电网没有得到充分的利用。

4.3 算例2

算例2运用二进制粒子群算法计算出最优的运行方式，在确定网架下用蒙特卡洛法（n=1 000）进行对比，如图4所示。

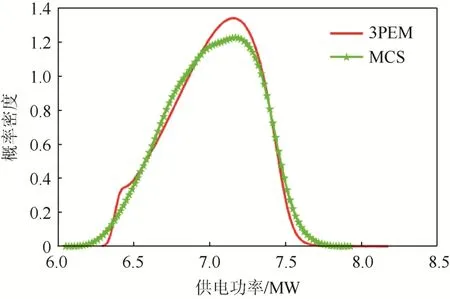
图4 两种方法得出的最大功率分布函数Fig. 4 Maximum power distribution functions obtained by the two methods

算例2重构优化得到的主动配电网网架结构如图5所示。

图5 重构后的主动配电网结构图Fig. 5 Structure diagram of active distribution network after reconfiguration

表4 重构开关动作Tab. 4 Switch actions of reconfiguration

进行重构优化后，在确定网架下用蒙特卡洛法（n=1 000）进行对比，计算结果如表5所示。

表5 算例2配电网供电能力指标（MW）Tab. 5 Indexes of power supply capacity of distribution network in example 2

通过对算例1和算例2的主动配电网供电能力分布函数比较可知，经过配网重构后供电能力值大幅度提升，重构前网络的供电功率期望ENSP为7.12 MW，通过重构得出的网络结构供电功率的期望为ENSP为18.84 MW，供电裕度也从重构前的55.8%增加到了重构后的330.3%，这都说明通过灵活改变运行方式可以提升配电网的供电能力。主动配电网供电功率的标准差从重构前的0.271增大到了重构后的0.695，说明主动配电网供电功率增大的同时供电能力的波动性也随之增大。

4.4 算例3

算例3为了说明DG接入对供电能力的作用，在算例2的重构后的网架下针对不同的DG接入配电网的情况计算相应的供电能力，具体情况如图6、表6、图7、表7所示。

图6 重构后两种方法得出的最大功率分布函数Fig. 6 Maximum power distribution functions obtained by the two methods after reconfiguration

表6 不同接入方案描述Tab. 6 Description of different access schemes

图7 不同方案下的最大功率分布函数Fig. 7 Maximum power distribution functions under different schemes

表7 算例3不同方案下的配电网供电能力指标（MW）Tab. 7 Indexes of power supply capacity of distribution network under different schemes

方案1～方案3的供电能力分别为：18.18 MW、18.65 MW和18.67 MW，供电裕度分别为315.2%、325.9%、326.3%，随着DG的增多电网整体的ENSP也相应增大，并且相应的供电能力标准差Dz也在不断增大，分别为0.536、0.723、0.728。

5 结论

为综合评估主动配电网的供电能力，本文分析了源、网、荷3方面对主动配电网供电能力的影响，首先提出评价主动配电网供电能力的新指标，其次通过三点估计法与重复潮流法相结合，运用Cornish-Fisher级数把样本点的各阶半不变量展开得到电网的供电能力分布函数，与MCS计算出的供电能力分布函数比较，证明方法的有效性。最后以分布函数的期望为目标函数，运用二进制粒子群算法计算出最有利于供电能力的运行方式。由实验结果看出DG的加入提升电网供电能力的同时也增大了供电能力的波动。而重构前后的供电能力各项指标对比可以发现运用网络重构能够大幅度提升主动配电网的供电能力与供电裕度。