基于Lambda方法的自衡对象PID整定研究

冯少辉，袁海雷

(上海华理自动化系统工程有限公司，上海 200237)

控制回路PID参数整定方法非常多，最有名的是JG Ziegler和NB Nichols在1942年发布的整定方法[1]。Ziegler-Nichols整定方法是规范化PID参数整定的鼻祖，开启了PID参数整定的科学化历程。很多大学课程中也主要介绍了该整定方法，但是实际中该整定方法存在很多问题，所以不推荐在实际工作中使用Ziegler-Nichols整定方法，该整定方法存在如下问题：

1)Ziegler-Nichols整定方法是为具有交互式控制器算法的控制器设计的。如果未使用微分(P或PI控制)，则这些规则也适用于非交互式算法。但是，如果使用微分(PID控制)并具有非交互式控制器或者控制器具有并行算法，则应转换计算出PID参数以使其适用于控制器。

2)整定方法以4∶1衰减振荡作为最佳控制回路性能，该方法会导致测量值超过其设定值并在其附近振荡几次，很多过程不允许超调，因此Ziegler-Nichols整定方法不适用这类对象。

3)Ziegler-Nichols整定方法得到的PID控制器鲁棒性不足，当工况变化后控制回路很容易振荡。

4)对于大纯滞后被控对象，控制回路由于积分作用太弱，控制回路的响应速度和抑制干扰能力都不理想。

传统整定方法关注克服不可测阶跃扰动时的峰值和累积偏差，这种积极但鲁棒性不足的整定方法不适合处理实际问题或实现其他控制目标。整定结果存在增益大、积分时间短的问题，不可避免地在系统中引起振荡，难以使系统达到整体性能最佳的控制目标，不适合大多数化工过程。新的整定方法关注增加鲁棒性、最小化非线性、耦合和振荡影响并满足其他过程目标，如： 最大化吸收干扰的缓冲罐液位控制、比值控制的回路协调和串级控制中底层回路的设定值响应等。

本文研究了基于Lambda方法的PID整定方法，并针对过阻尼和欠阻尼自衡对象给出了参数设置的方法，最后使用该方法对大纯滞后欠阻尼对象进行了仿真验证。

1 Lambda整定方法

20世纪80年代之前的大多数参数整定方法都关注克服不可测阶跃扰动时的峰值和累积偏差，这种积极行为对防止激活减灾系统或触发停车条件非常重要，但是由于鲁棒性不足不适合处理实际问题或实现其他控制目标。

Lambda整定方法是用于减少过程波动的成功方法。从最简单的意义上讲，Lambda整定以所需的期望闭环响应速度实现控制回路的非振荡响应，通过选择一个期望闭环时间常数(通常称为λ)来设置响应速度。通过选择期望闭环时间常数，可以在一个单元过程中协调一组控制回路的PID整定，从而通过它们的共同作用建立整个过程的理想动态。

Lambda整定概念的基础可以追溯到1957年Newton，Gould和Kaiser的分析设计方法[2]。简而言之，一旦知道了过程模型并且选择了期望闭环特性，该方法就可以直接合成所需的控制器。1968年，EB Dahlin在数字控制器上的工作为Lambda整定提供了主要推动[3]。Dahlin将所需的闭环响应速度描述为“Lambda”。Dahlin只关心一阶纯滞后对象，而Morari和Chien等人将该技术推广到一般的传递函数[4-5]。该设计方法的基础是零极点配置，其中控制器零点用于抵消过程极点。

Lambda整定方法是针对速度的整定方法(例如Ziegler-Nichols法、Cohen-Coon法等)的强大替代方法。Ziegler-Nichols法、Cohen-Coon法的目标是4∶1衰减振荡，而Lambda整定方法的目标是一阶纯滞后对设定值的响应。Lambda整定方法具有以下优点[6]：

1)过程变量在发生干扰或设定值变化后不会超调。

2)Lambda整定方法对通过阶跃测试确定过程纯滞后时间时所犯的任何错误的鲁棒性比较高。该类问题在时间常数为主的过程中很常见，因为很容易低估或高估了过程纯滞后时间。当纯滞后时间不正确时，Ziegler-Nichols和Cohen-Coon整定方法可能会给出非常糟糕的结果。

3)整定鲁棒性好，意味着即使过程特性与用于整定的过程相比发生了较大变化，控制回路也能保持稳定。

4)Lambda整定的控制回路可以更好地吸收干扰，并将更少的干扰传递给下游过程。对于高度耦合过程，这是一个非常有吸引力的特性。造纸机上的控制回路通常使用该整定方法进行整定，以防止整个机器由于过程相互耦合和反馈控制而发生振荡。

5)用户可以为控制回路指定所需的响应时间(实际上是闭环时间常数)，这提供了一个期望闭环响应时间常数λ作为整定因子，可用于加快或减慢回路响应。

Lambda整定期望的第一步是计算λ。λ描述控制器响应设定值阶跃变化时的速度。因此，一个较小的λ(即短响应时间)意味着一个积极的控制器或一个以快速响应为特征的控制器。

Lambda整定方法简化过程如图1所示。

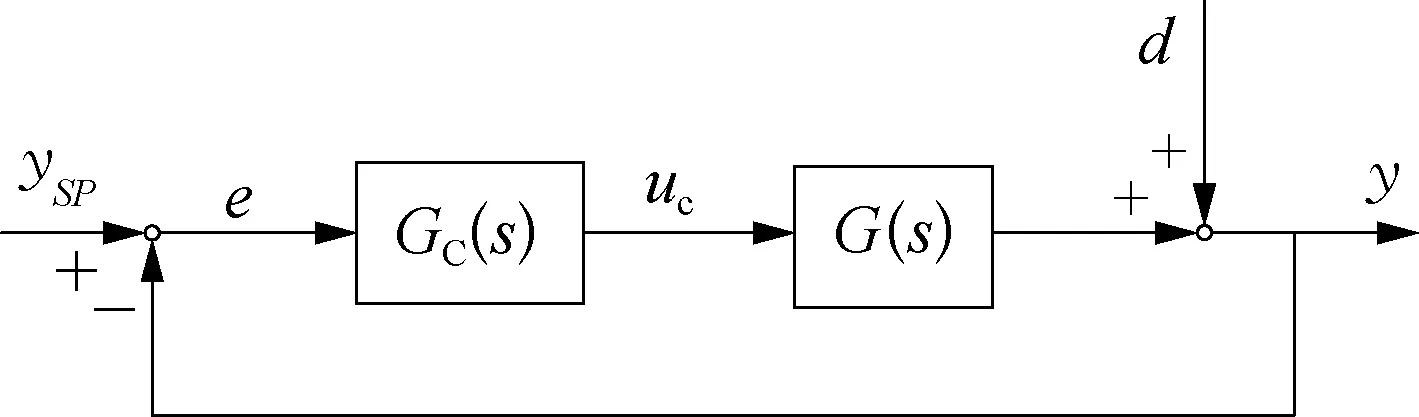
图1 Lambda整定方法简化过程示意

主通道闭环传递函数为

(1)

控制器传递函数为

(2)

(3)

被控对象为一阶纯滞后模型，其传递函数为

(4)

期望的闭环传递函数为

(5)

闭环控制不能消除纯滞后时间，所以设闭环传递函数仍有固定纯滞后。

将式(5)代入式(3)得：

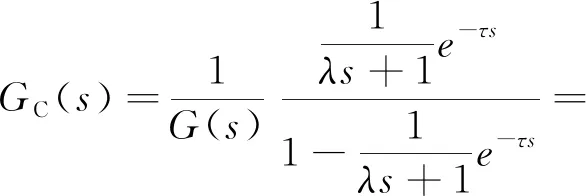
(6)

将式(4)代入式(6)得：

(7)

对式(7)中的纯滞后使用一阶Taylor展开近似：

e-τs≅1-τs

(8)

将式(8)代入式(7)得：

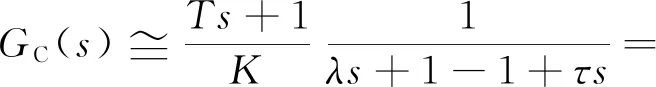
(9)

故：

(10)

当λ=0.6τ，闭环的设定值会和Ziegler-Nichols整定方法类似得到4∶1衰减振荡的响应。当λ=τ，闭环的设定值跟踪会超调但不振荡，这也是Lambda整定方法推荐的最强控制作用。当λ=2τ时，闭环设定值跟踪不超调。Lambda整定方法推荐的鲁棒参数为λ=3τ。λ的选择和开环对象的纯滞后直接相关。

2 基于实际对象的Lambda参数整定方法

在实际自衡对象中，大部分都不是标准的一阶纯滞后对象，而是如图2所示的过阻尼多容对象开环响应或者如图3所示的欠阻尼对象开环响应。针对该类对象可以使用分析设计方法，基于内模控制理论得到PID参数，但是往往由于被控对象的模型过于复杂，很难得到合适的参数。本文提出一种方法： 由于获得模型是为了进行PID参数整定，所以可以根据阶跃响应曲线使用近似的方法获得Lambda整定需要模型的增益K，时间常数T和纯滞后时间，然后再给出一个满足条件的λ，使用这4个参数就能根据式(10)得到PID参数。

对于自衡对象而言，模型增益无论使用开环还是闭环测试，计算公式均为K=ΔPV/ΔOP。

从开环响应的63.2%ΔPV，沿响应曲线向前做响应曲线的切线，切线与时间坐标轴相交。输出变化到交点为纯滞后时间，交点到63.2%ΔPV的时间为T。过阻尼多容对象的开环阶跃响应如图2所示，欠阻尼对象的开环阶跃响应如图3所示。

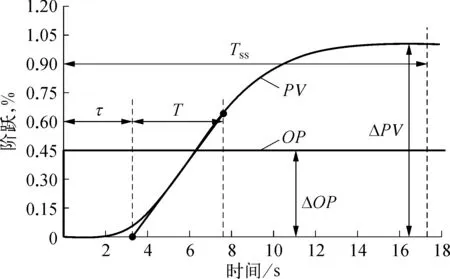
图2 过阻尼多容对象开环阶跃响应示意

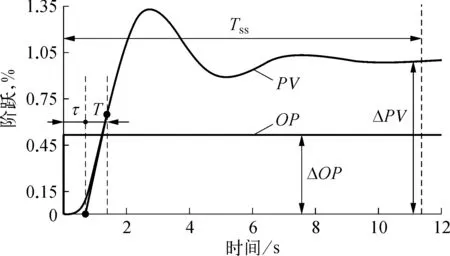
图3 欠阻尼对象开环阶跃响应示意

考虑被控对象的复杂性，推荐λ：

(11)

式中：Tss—稳定时间，即阶跃开始时到PV稳定时的时间。

3 仿真试验

被控对象传递函数：

(12)

被控对象的开环阶跃响应曲线如图4所示。该被控对象为大纯滞后欠阻尼自衡对象，针对这种对象一般使用常规的方法很难得到合适的PID参数。

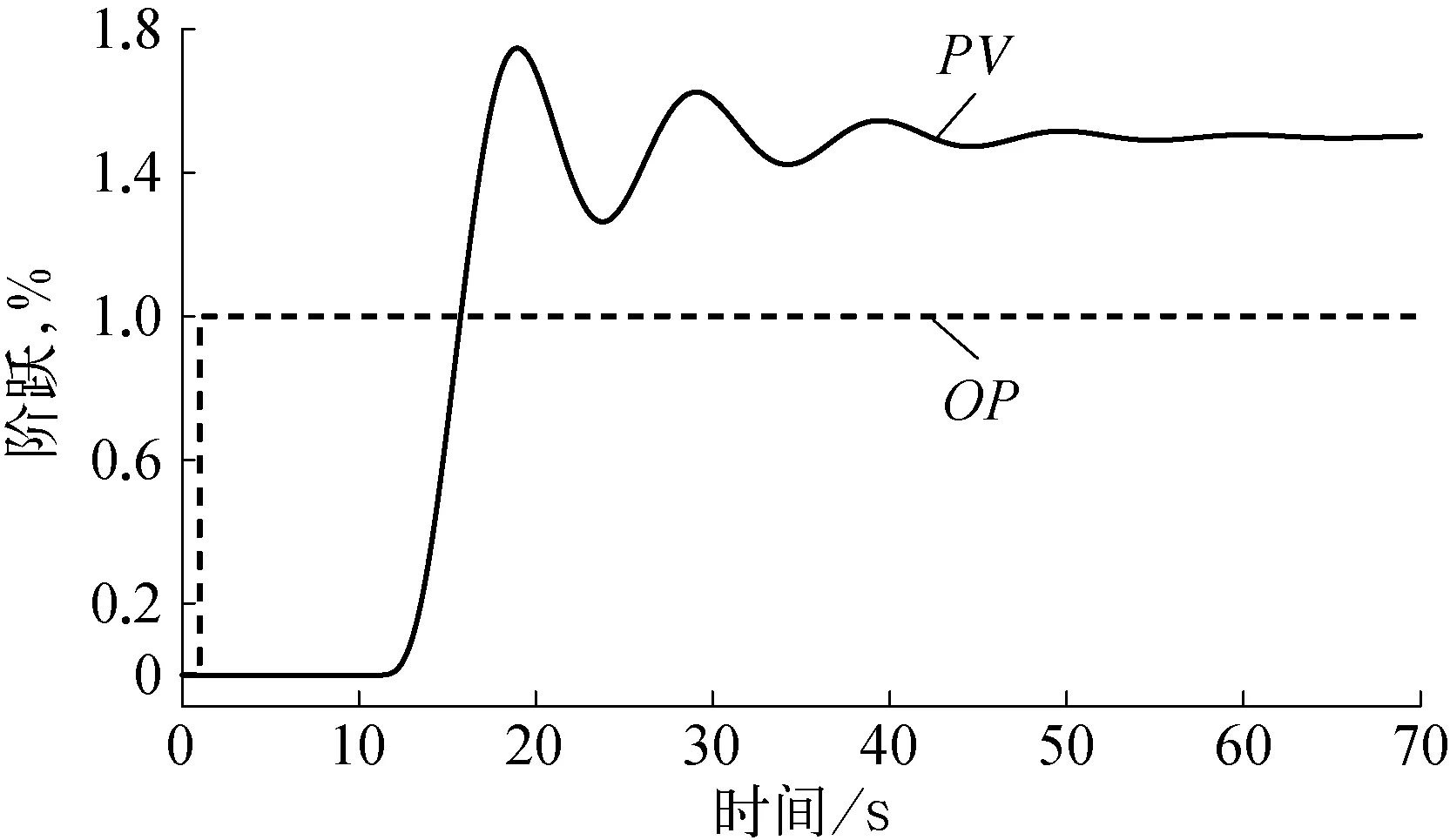
图4 被控对象的开环阶跃响应曲线示意

使用类似图3的方法可以得到对应的一阶纯滞后被控对象模型：

(13)

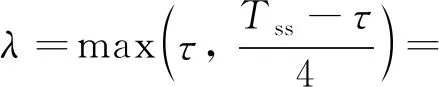
(14)

根据Lambda整定方法，可得到如下的控制器参数：

(15)

使用Lambda整定方法得到的PID控制器参数进行设定值阶跃变化仿真，被控对象的闭环阶跃响应如图5所示。

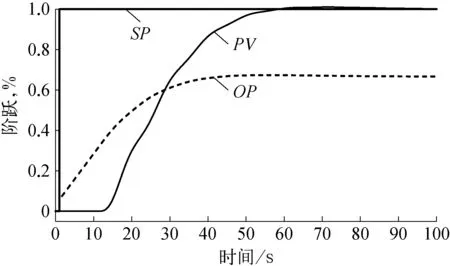
图5 被控对象的闭环阶跃响应曲线示意

由图5可知，在被控对象极其复杂的情况下，使用本文给出的Lambda整定方法仍可以一次得到适用的PID初始参数。

4 结束语

Lambda整定方法具有适用的被控对象特性广、控制器设定值跟踪无振荡的良好特性，是一种值得推广的PID参数整定方法。该方法针对过阻尼的多容自衡对象同样有效，在该整定方法中不涉及微分，在多容特征明显时适当的加入微分也是一个选项，但是微分时间不宜设置的太大。