超宽频带声涡旋装置的调制与研究

2021-08-04林梓彬许卫锴刘成龙祁武超

沈阳航空航天大学学报 2021年3期

林梓彬，许卫锴，刘成龙，祁武超

(沈阳航空航天大学航空宇航学院，沈阳 110136)

超材料(Metamaterial)是一种具有特殊性质的、自然界中不存在的人工材料，通过精心设计材料的几何结构而非改变材料自身成分的方式，使得超材料具有负质量密度和负弹性模量等特性，从而达到波控的目的[1-2]。超表面(Metasurface)作为超材料的一个重要分支，可以看作是超材料轻薄化的结构产物[3]，其最显著的特征就是它的厚度远小于波长，即具有亚波长厚度。因此，相对于三维的超材料来说，超表面不但能显著地节省物理空间，还能大幅降低材料成本。与超材料首先在电磁波领域实现类似，超表面的首次提出也是在光学领域，随即引起了很多科研工作者的关注，并迅速在声学领域设计出几种经典的构型，如迷宫型超表面[4]、亥姆霍斯谐振型超表面[5]及薄膜型超表面[6]。然而，上述超表面往往存在带宽较窄、阻抗失配或者结构脆弱的缺点，因此研究新型的超表面显得尤为重要。2016年，Zhu等[7]设计出嵌入式塔型超表面来实现异常折射，Yuan等[8]利用“鱼骨型”结构实现可调弹性超表面，通过构建不同结构单元的超表面，扩大其应用场景，能够实现更多的功能如自弯曲声束、低频完美吸声、涡旋声束等[9-12]。

随着研究人员对弹性波超表面的深入研究，其更多特性逐渐进入人们的视野，具有螺旋形相位位错的弹性波涡旋场近来受到了大量关注。如同我们日常生活中熟悉的水涡和气涡，弹性波涡旋场也是携带角动量的涡旋现象。但与自然界中的涡旋现象不同的是，弹性波涡旋是人为的在波涡旋场中施加激励，通过弹性波超表面这种特殊的结构使所加激励产生类似涡旋场的现象。弹性波涡旋所产生的力学效应有一定的应用场景，例如Rohde等[13]以超材料孔隙为基础设计的涡旋波天线。在声涡旋方面，“声波镊子”和“声波起子”[14]得到了研究人员深入的研究，前者可以利用声辐射力对微小物体实现精准操控[15-16]，例如将其俘获在特定的空间位置[17]，后者利用声涡旋特有的角动量远程传递能力，能够在不接触物体的情况下，远距离施加一个扭矩使之旋转[18]。

然而，对于上述弹性波涡旋场来说，都是在特定频率范围内实现预期效果，工作带宽相对较窄。本文对所提出的凹槽型超表面进行研究，通过精心设计凹槽列阵，实现了宽频带的涡旋效应，结果对声波的调控及弹性波涡旋场的建立提供了一定的参考意义。

1 涡旋声束的基础理论

1.1 广义斯涅耳定律

当声(光)波从一种介质传播到另一种介质时，入射角与折射角之间的关系可以用斯涅耳定律来表示，即

(1)

其中，θi和θt分别为入射角和折射角，λi为入射波长，λt为折射波长。Yu等[19]指出，根据费马原理，若在交界面引入一个相位变化来改变波的传播路径，则原有的反射和折射角度将会产生异常的效果，此时入射角与折射角的关系需要改写为广义的斯涅耳定律

(2)

其中，dφ(y)/dy是沿界面切向的相位梯度，经整理后折射角度变为

θt=arcsin[(λtsin(θi)/λi)+(λt/2π)(dφ(y)/dy)]

(3)

从式(3)推导出的折射角与相位梯度的关系式看出，通过引入相应的相位函数dφ(y)，可以任意调控折射角度。当这个相位函数为0，即不存在超表面的相位梯度时，式(2)就是传统意义上的斯涅耳定律表达式。

1.2 相位调制机理

超声兰姆波在薄板的无损检测中有着重要的作用，其中兰姆波与缺陷的交互作用得到了广泛的研究[20]。由于兰姆波到达缺陷后会发生模态转换和散射衰减，难以直接进行信号分析。早期的研究主要考虑波的透射与反射，例如，Rokhlin等[21]对兰姆波与焊接缝的交互作用进行研究，分别从数值求解和实验的方法研究了兰姆波在焊缝处的反射和透射系数。Alleyne等[22]同样用数值方法研究了兰姆波与槽型缺陷的交互作用。Benmeddour等[23-24]则分别对对称/非对称的槽型缺陷与兰姆波的交互作用进行了研究。相对而言，目前关于凹槽型缺陷对相位影响的研究较为稀少。

根据惠更斯原理，兰姆波到达凹槽后会发生模态转换，这时可将其视为新的波源。此时薄板中的质点运动位移满足Navier质点平衡方程

(4)

其中，u是质点振动位移矢量，μ和λ是兰姆波拉梅参数。兰姆波在薄板中传递时有两个模态：对称模态(S-mode)和反对称模态(A-mode)。在对称模态兰姆波下，薄板中心质点作纵向振动，上下表面质点作椭圆运动且振动相位相反并对称于中心；而在反对称模态兰姆波下，薄板中心质点作横向振动，上下表面质点作椭圆运动，相位相同且不对称于中心。由兰姆波理论[25]可知，当薄板处于自由边界条件下，即薄板的界面处正应力和切应力为零时，对称模态和反对称模态兰姆波在传递过程中都会出现散射现象，通过势函数分解的方法求解式(4)可得到对称模态和反对称模态兰姆波的频散特性方程，即Rayleigh-Lamb波散射方程[26-27]

(5)

(6)

近日，浩鲸科技携手南京市公安局交通管理局打造的智慧交通综合应用平台二期项目正式通过初验。该平台整合一期项目数据和“一标三实”信息采集会战数据，可广泛用于开展路况拥堵态势分析、道路拥堵分析及大队工作监管等,助力南京市公安局交通管理局推进以大数据研判为支撑，信息主导警务的智慧新交管建设，帮助交警在面对日益复杂的道路状况和出行场景时，有效提升交通管理效能。

(7)

将角频率公式ω=2πf与式(7)整理得到群速度与相速度的关系

(8)

其中，fh为频厚积，从式(8)可以看出，频厚积影响着兰姆波相位的传递，板厚度不同时，兰姆波传递的相位也会随之发生改变。因此，凹槽型超表面可以看作是无损检测的反问题：无损检测中利用兰姆波的信息判断缺陷的位置，而通过人为制造不同位置的凹槽缺陷来实现兰姆波的相位调制。本文利用有限元仿真软件COMSOL Multiphysics对凹槽单元的相移进行计算。图1中展示了凹槽结构的单胞以及根据数值仿真结果得到的凹槽位置与相位变化的关系曲线，单胞的几何参数如表1所示。

从凹槽位置与相位变化的关系曲线中，可以观察到随着凹槽的位置改变，兰姆波的传递相位实现了0～2π的变化，由于凹槽缺陷的尺寸很小，因此可选取对相位影响较大的位置信息作为调制变量，结合广义斯涅耳定律[19]可以实现一系列兰姆波的调制。

1.3 含角动量的涡旋公式

具有螺旋形相位位错的声涡旋场能够实现角动量的传递，产生可以远程局域或者旋转物体的力矩，在粒子操控等领域具有十分重要的意义。本文设计了一种基于凹槽型超表面的声涡旋装置，可以人为添加一个额外的角动量n，这个额外的角动量使得构型中心所激发的点源在经过超表面基本单元排列的结构之后产生涡旋线，在此需要说明，角动量n应为整数以保证产生的涡旋线的条数同样也为整数。通过引入角动量的方式，能够实现对源的改变，这时的源将类似一个涡旋源，呈现出带有螺旋波前的点源形态，所需要的相位突变轮廓如式(9)所示。[13]

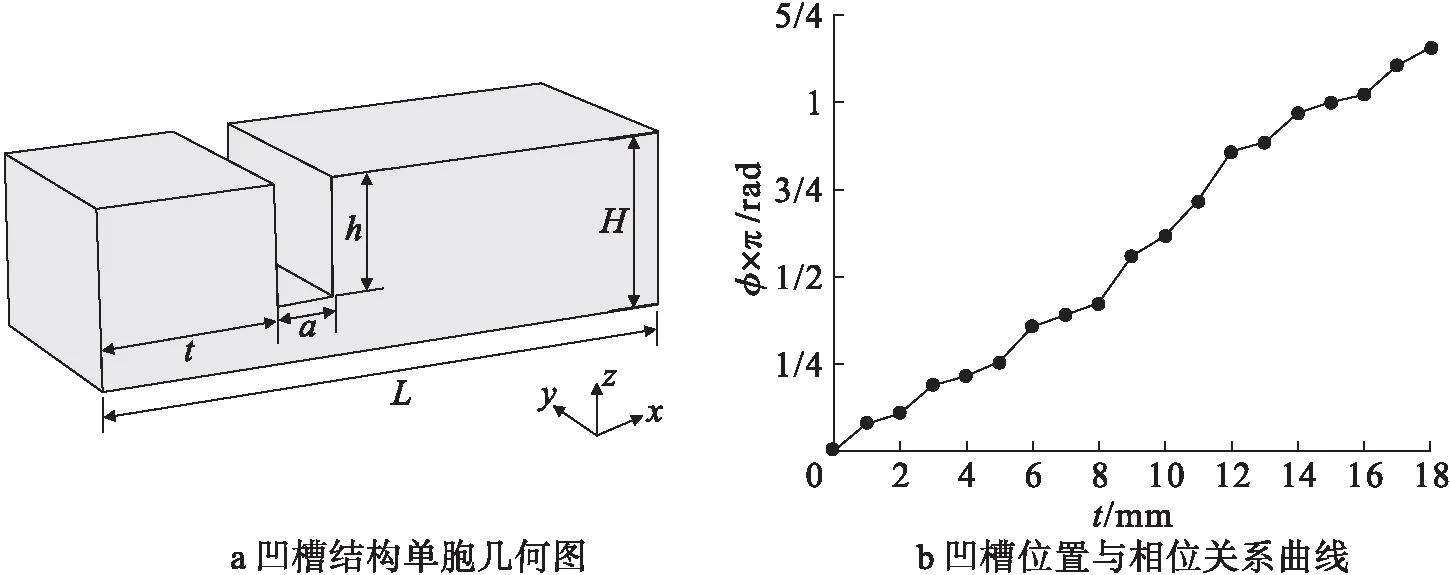
图1 凹槽结构单胞几何及凹槽位置与相位关系曲线图

表1 凹槽结构单胞几何参数

θtar-θori=nθ+θ0

(9)

其中，θori为波源的相位轮廓线，θtar为目标波的相位轮廓线，n为所添加的额外的角动量个数，θ为方位角，θ0为任意的常数。这样就可以通过调整角动量n的数值来调制相应的涡旋场。

2 算例分析

2.1 装置模型

涡旋源装置如图2所示。在平板上有一点源，可激发兰姆波。为使该点源能够产生涡旋场，需在其周围布置一环形的超表面如图2a所示。选取对相位影响最为明显的凹槽位置t作为调整超表面非连续相位的参数，通过严格按照相位变化近线性关系曲线对不同凹槽进行排布，可在2π周期内实现相位变化，进而实现兰姆波的波场调控。文中选取金属铝板作为涡旋源装置超表面的材料，其材料参数如表2所示。

表2 超表面材料(铝)参数

图2 涡旋源装置及功能单元结构图

2.2 仿真结果与讨论

对图2a所示装置进行仿真分析。不失一般性，令n=4，即希望产生4条涡旋线。这需要将环形超表面分为4组，如图2b每组由10个单胞构成以实现连续相位变化的调制。在仿真过程中，在点源处施加一个z方向的单位长度力来模拟A0模态的兰姆波激励，内圆θori和外圆θtar用于区别兰姆波经过凹槽前后波的传播样式，相应的Rori=56 mm，Rtar=73 mm。为了减少边界上的反射，防止兰姆波被边界反射回来影响仿真效果，在结构的四周添加了完美匹配层(PMLs)以吸收进入域内的所有波。

图3 n=4时环形超表面调制生成的涡旋场示意图

为了进一步验证该装置的鲁棒性，分析了角动量n分别为2、3和5的情况，即将基本单元圆周排列为2组、3组和5组。为节省篇幅，以上3种情况统一选择频率为7.2 kHz和35.6 kHz进行仿真并分析结果。图4展示了角动量n为2、3和5时2个频率下的中面面外位移场。从仿真结果可以看出，中心点所激发的兰姆波在经过涡旋装置之后，分别呈现出2条、3条和5条涡旋线。这说明所设计的环形超表面能够在保证涡旋效果的同时，实现多种涡旋场的调制。