基于旋量理论的全方位移动机器人运动与误差分析

叶长龙，王 瑞，赵 东，于苏洋

(沈阳航空航天大学 机电工程学院，沈阳110136)

全方位移动机器人以其全方位运动特性被广泛关注和应用，尤其在一些特殊场合，如装配车间，其作为移动装配机器人的运动平台，使装配变得更加灵活方便[1-2]。为了满足高端装配需要，仍需进一步分析其运动及误差以寻求提高运动精度的方法。

目前机器人的运动学分析建模与误差分析建模多采用速度适量法[3]和矩阵法[4]。然而当同一构件两端关节的轴线互相平行时，参数的微小变化将导致末端位姿的阶跃，使得机构运动学模型中的参数映射不连续，若采用旋量方法会避免这种情况发生。荆学东等[5]应用螺旋公式使用矩阵指数和指数积建立了机器人运动学模型。Yi BJ等[6]用旋量理论建立了移动平台的运动学模型。Moon等[7]将旋量矩阵微分获得机器人的的误差矩阵。

本文应用虚拟连杆原理[8-10]和旋量理论方法[11-14]，以实验室研发的基于MY4轮的全方位移动装配机器人(MY4-robot)为研究对象，建立其运动学模型与误差模型，分析了各误差对装配精度的影响，最后提出改进方法。

1 全方位机器人运动学模型

1.1 MY4-robot

图1为实验室自主研发的MY4-robot试验样机,主要包括全方位移动平台和并联装配平台两部分，末端执行器安置于O1点。其结构与文献[15]中MY3-robot的不同仅在于其全方位移动平台采用并联式MY轮组(即MY4轮)结构，MY4-robot相关参数如表1所示。

1.2 全方位机器人运动学模型建立

1.2.1 全方位移动平台的运动学模型

MY4-robot底盘轮结构布局如图2所示，4组MY4轮组均匀布置，编号1～4，αj为j号轮组的布置角。移动平台坐标系xroryr与实际坐标系xwowyw重合。or为平台的几何中心，设定平台在图2a所示位姿为初始位姿。

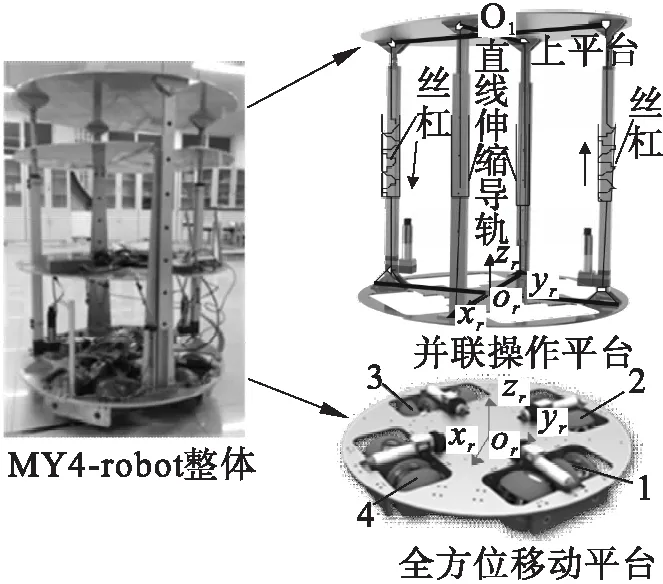
图1 MY4-robot样机

表1 机器人的结构性能参数

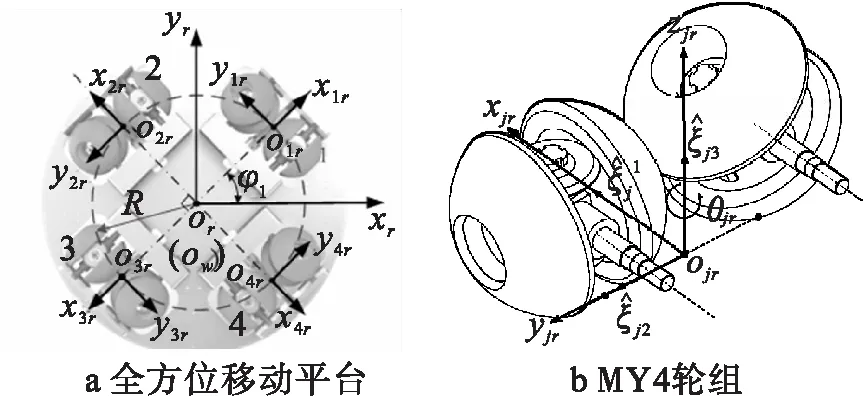
图2 全方位移动平台结构

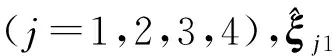
全方位移动平台的运动可看作：沿xw方向的平移sx，沿yw方向的平移sy及绕几何中心or的自转θr。如图3所示，此时世界坐标系为固定基，机器人的位姿变化为xr→x′ry′r→x″ry″r。

图3 全方位移动平台运动分析

由于MY4轮组的驱动始终沿yjr轴方向，为了得到MY4轮组速度与全方位移动平台运动速度的关系，选取变化后轮组坐标系为固定基，以1号轮组为例，如图4所示。

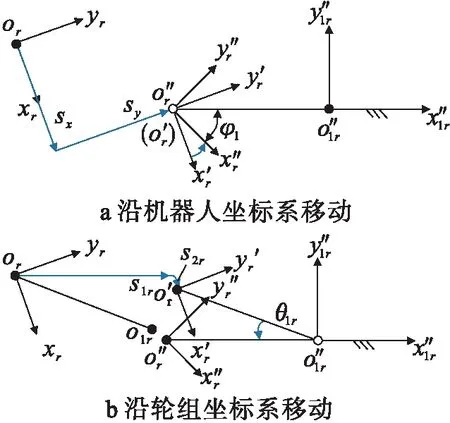
图4 1号轮组为固定基

当移动平台按如图4a方式运动时，全方位移动平台的运动学正解指数积POE公式为

(1)

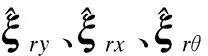
移动平台按图4b所示方式运动也可以到达x″ry″r位姿，全方位移动平台的运动学正解指数积公式为

(2)

由公式(1)、(2)得到螺旋运动方程

(3)

式(3)中：ξ11=[0,1,0]T、ξ12=[0,0,1]T、ξ13=[1,0,0]T、ξrx=[0,cθrφ1,-sθrφ1]T、ξry=[0,sθrφ1,-cθrφ1]T、ξrθ=[1,0,R]T，表示移动平台运动后的运动旋量坐标，其中cθrφ1=cos(θr+φ1)，sθrφ1=sin(θr+φ1)。

轮组驱动只沿yjr轴方向，故由式(3)取得

(4)

同理综合2、3、4号轮组可得到全方位移动平台的逆运动学模型

ψP=JP·VP

(5)

式(5)中：VP=[ωP,vx,vy]T，为全方位移动平台速度矩阵；ψP=[v1,v2,v3,v4]T，为4组轮组驱动速度矩阵；

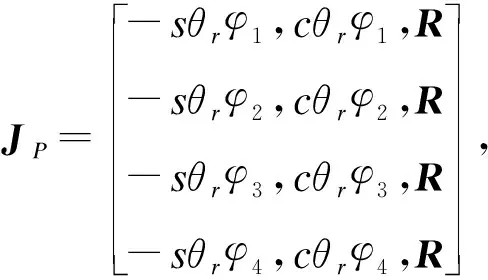
1.2.2 并联装配平台的运动学模型

并联装配平台的驱动丝杠实现举升平台上下的伸缩运动，直线伸缩导轨对上平台起到一定的限位作用，使上平台只能绕着导轨的上铰接位置翻转，所以并联装配平台具有两个自由度：即通过两侧的丝杠实现上平台沿着z轴方向的举升和绕着x轴翻转，所以针对并联机构的运动只需要在zroryr面内进行分析。

图5为并联机构的zr-or-yr面内结构简图。图5中，θ10、θ11、θ21、θ30、θ31、S1、S2、S3表示关节变量，{S}表示惯性坐标系，{T}表示工具坐标系，末端执行器固定于O1点。并联机构包括3条子链：1号链P0-P1-O1，2号链Or-O1，3号链Q0-Q1-O1。为了简化计算,取如图5所示时刻为参考位姿。

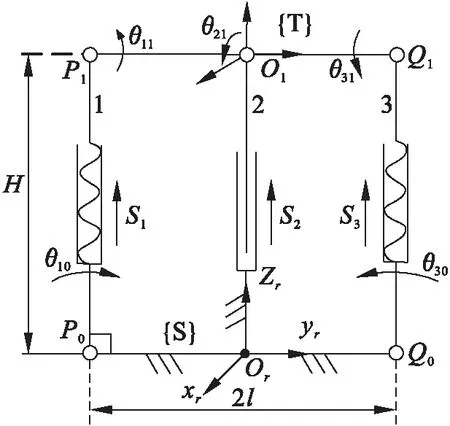
图5 并联机构zr-or-yr面内结构简图

图5中3条子链的运动学正解指数积公式为

(6)

(7)

(8)

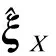
由公式(6)、(8)得到螺旋运动方程

(9)

式(9)中：ξP0=[1,0,l]T、ξ′P1=[1,acθ10,l-asθ10]T、ξS1=[0,sθ10,cθ10]T，表示并联机构运动后1号链各运动副旋量；ξO1=[1,b,0]T、ξS2=[0,0,1]T，表示并联机构运动后2号链各运动副的旋量坐标。

其中a=H+S1，(b=H+S2，c=H+S3)，sθ10=sinθ10，cθ10=cosθ10，后文采用同样的表达方式。

(10)

同理，由式(6)、(7)推导可得

(11)

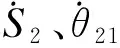
通过式(10)、(11)的相加与相减，得到并联机构的逆运动学模型

ψb=Jb·Vb

(12)

式(12)中，Vb=[ωb,vz]T，为并联装配平台末端速度矩阵；Jb=(pη1-qμ1)·(pη2-qμ2)，为逆雅克比矩阵，p=[ξP0+ξP1,ξQ0-ξQ1]+、q=[ξP0+ξP1,ξQ1-ξQ0]+、μ1=[2ξS2,2ξO1-ξP1-ξQ1]、η1=[0,ξQ1-ξP1]、μ2=[ξS1,ξS3]、η2=[ξS1,-ξS3];ψb=[vs1,vs3]，为丝杠伸缩的线性速度。

综合式(5)、(12)得到全方位移动机器人的整体逆运动学模型

ψr=Jr·Vr

(13)

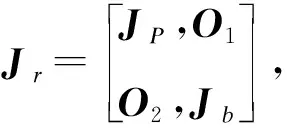
2 全方位移动机器人误差模型

2.1 移动平台误差模型

式(5)两边同时乘以dt，可得到移动平台的简单误差模型

(14)

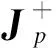
2.2 仿真分析

图6 移动平台位置误差仿真结果

通过比较图6中的仿真结果发现平台的位置误差随着平台姿态周期性变化而呈现出正余弦周期性变化。分析图6b、6c、6d、6f和6g，全方位移动平台位置误差幅值由图6b中的0.707 mm升到6f中的1 mm和降到6c、6d及6g中接近于0 mm可知，对称位置轮组的驱动误差同向相等时可抵消对平台位置误差的影响，但对称轮组驱动误差反向时反而会增加对平台位置误差的影响。比较图6a和图6h，移动平台位置误差幅值由6a中的0.5 mm降到6h中的0.05 mm表明平台的位置误差与轮组驱动误差成正比；图6b和图6e对比分析，位置误差幅值都为0.707 mm可知，非对称轮组驱动误差的方向不会改变平台整体位置误差峰值大小，只会改变平台达到位置误差峰值时的姿态角度。

图7中的仿真结果表明平台的姿态误差与平台起始姿态角无关。图7a表明随着存在误差的轮组数量的增加平台的姿态误差增大；图7b表明平台姿态误差随着轮组驱动误差的增大而增大；分析图7c发现轮组间驱动误差方向相反时对平台姿态误差的影响有抵消作用。上述发现为降低该类全方位移动平台位姿误差提供了参考依据，即可以通过采取合适的控制方法提高各对称位置轮组驱动误差的同步性来降低平台的位置误差。同时，在单轮驱动精度很难进一步提高的情况下，转而调整控制算法使轮组间驱动误差方向相异，以达到进一步降低平台姿态误差的目标。

3 实验

3.1 移动平台实验

移动平台的仿真轨迹为

(16)

仿真结果如图8所示。

在地面上粘贴长半轴为1 000 mm，短半轴为600 mm的椭圆理想轨迹，带宽16 mm。机器人的运动过程如图9所示。图10显示了移动平台在运动过程中的实际轨迹，其中黑色区域为标定理想轨迹域，白色线条为记录的实际轨迹。

因为机器人轮子驱动误差很难定量控制，实验中通过人为设定速度偏差，忽略不可控误差，以验证结论的正确性。通过图9、图10可以看出机器人成功地完成了设定的轨迹运动，说明对称轮组驱动误差同向相等时可抵消对平台位置误差结论的正确性，同时也验证了运动学模型的正确性。

图8 仿真结果

图9 机器人跟踪轨迹实验

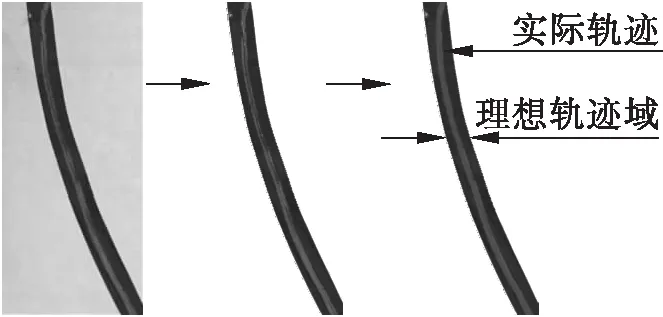
图10 实际轨迹

3.2 举升翻转实验

并联平台的仿真轨迹为

(17)

仿真结果如图11所示。

对并联装配平台进行了两组实验，两组实验分别为举升实验(如图12所示)和翻转实验(如图13所示)。实验采用分辨率为0.1°的数字螺距尺来测量上平台的翻转角度，通过海克斯康视觉检测系统来测量其举升高度，其分辨率为0.1 mm，在实验过程中放置重物的重量为6 kg。两组实验的实验数据如表2、表3所示。

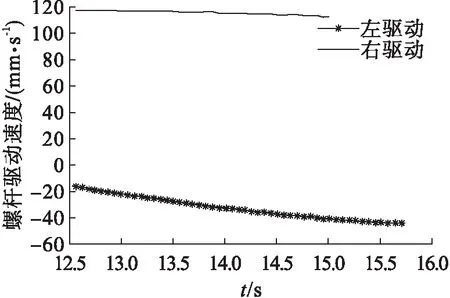
图11 仿真结果

图12 举升实验

图13 举升实验

表2 举升实验数据

通过分析实验数据发现，基于运动学旋量模型的举升和翻转实验误差分别在1 mm和1°左右，验证了并联装配平台运动学模型的正确性，但与高精密作业精度要求还有差距。

4 结论

本文应用旋量理论的指数积公式建立了全方位移动装配机器人的运动学模型，避免了位姿阶跃。速度矢量方法建立的移动平台运动学模型是先确定轮的驱动方式后建立模型，而旋量方法可以一次得到多种运动学模型，然后根据实际选取的驱动方式得到特定的运动学模型，通过仿真实验与样机实验验证了这种建模方法的有效性。并在此基础上，应用旋量理论的指数积公式结合虚拟连杆原理建立了全方位移动装配机器人的误差模型。通过仿真实验分析这种关系得到如下结论：

(1)对于该类全方位移动平台，对称的轮组的驱动误差相近时平台的位置误差会减小，平台的姿态误差与轮组的误差始终成正比，非对称轮组驱动误差的方向不会改变平台整体位置误差幅值大小，其只会改变平台达到位置误差峰值时的姿态角度；

(2)随着存在误差的轮组数量的增加平台的姿态误差增大，平台姿态误差随着轮组驱动误差的增大而增大，轮组间驱动误差方向相反时对平台姿态误差的影响有抵消作用。

通过分析仿真结果提出几点改进措施：

(1)根据全方位移动机器人在X和Y方向的精度要求的不同，调整机器人的姿态角度从而提高机器人在某一方向(如X和Y方向)的精度要求；

(2)在满足运动要求前提下，采用尽量少的驱动轮组数量;

(3)提高铰接的内孔与杆长的尺寸精度，以进一步提高整体运动精度。以上措施为该类全方位移动机器人运动精度的深入研究提供参考。