交错控制双输入Boost变换器的能量传输模式及输出纹波电压分析

皇金锋 韩梦祺

（1.陕西理工大学电气工程学院 汉中 723001 2.陕西省工业自动化重点实验室 汉中 723001）

0 引言

传统采用多种能源供电的分布式发电系统，每种能源均需要一个 DC-DC变换器，导致这种发电系统存在结构复杂、成本高等缺点[1-6]。多输入DC-DC变换器代替传统单输入变换器不仅可以简化电路拓扑结构、降低成本，还可以提高系统供电可靠性，因此，多输入 DC-DC变换器在多种能源联合供电的分布式发电系统中有广阔的应用前景[7-9]。

近年来，国内外学者对多输入直流变换器进行了深入研究[10-15]。文献[11]提出一种双输入 Boost变换器，两个变换器连接到同一直流母线上，通过对每一个变换器单独控制，可以实现对功率和输出电压的有效控制。文献[12]提出一种高增益非隔离多输入 DC-DC变换器，该变换器工作模式简单，并可以通过选择较高的开关频率来降低输入电流纹波。文献[13]提出了采用交错控制的多输入高升压Boost变换器拓扑，并以双输入为例进行分析讨论。该变换器不仅能提高升压比，还能通过调节各功率开关管的占空比来实现变换器的最大功率跟踪。文献[14]提出含有开关电容单元的双输入 Boost变换器，该变换器不仅电压增益高，还能实现两路输入单独供电，提高了供电的灵活性。文献[15]针对电容串接式交错并联Boost变换器全占空比范围内不均流现象，提出不对称占空比的均流控制策略，该均流策略无需额外增加电流传感器，仅改变其中一相电流的占空比就可以实现变换器在全占空比区域内的电流共享。以上研究提出的多输入 DC-DC变换器电路拓扑或控制策略均能有效地提高变换器的电压增益或改善系统性能。

双输入 Boost变换器因其电路拓扑的特殊性以及控制方式灵活等特点，导致其供能模式和输出纹波电压较传统 Boost变换器要复杂得多，而供能模式和输出纹波电压是衡量变换器性能的重要指标，同时也是变换器参数设计的重要依据[16-19]。合理地设计变换器参数，不仅能提高变换器工作效率及稳定性，还能改善系统的暂态性能[20]。但现阶段国内外文献对双输入Boost变换器的供能模式和输出纹波电压的分析不够深入，其参数设计缺乏理论依据。

为给双输入Boost变换器的分析和设计提供正确的理论依据，本文对交错控制双输入 Boost变换器的供能模式及纹波电压进行深入研究，推导出各供能模式的临界电感和输出纹波电压解析式，据此给出了变换器参数设计方法。同时对多输入 Boost变换器的供能模式进行了归纳总结，并对电感L1工作于完全电感供能模式（Complete Inductor Supplying Mode, CISM），其余电感工作于电流连续模式（Continuous Current Mode, CCM）时的纹波电压特征进行分析，研究结果对多输入 Boost变换器的分析设计具有指导意义。

1 能量传输模式

双输入Boost变换器的电路拓扑如图1所示。该拓扑由开关管S1和S2、电感L1和L2、二极管VD1和VDo、电容C1和Co以及负载RL构成。采用交错控制时双输入Boost变换器的开关管占空比存在D＞0.5和D＜0.5两种情况，对应两种工作模式，由于两种工作模式的分析方法类似，限于篇幅，本文仅以D＞0.5为例对其供能模式和输出纹波电压进行分析，设开关周期为T，其不同工作模态的等效电路如图2所示，电感电流与电容电压波形如图3所示。

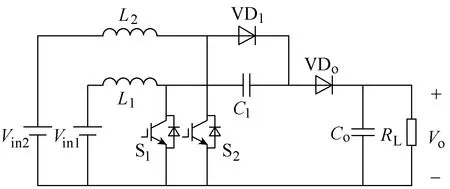
图1 双输入Boost变换器Fig.1 Dual-input Boost converter

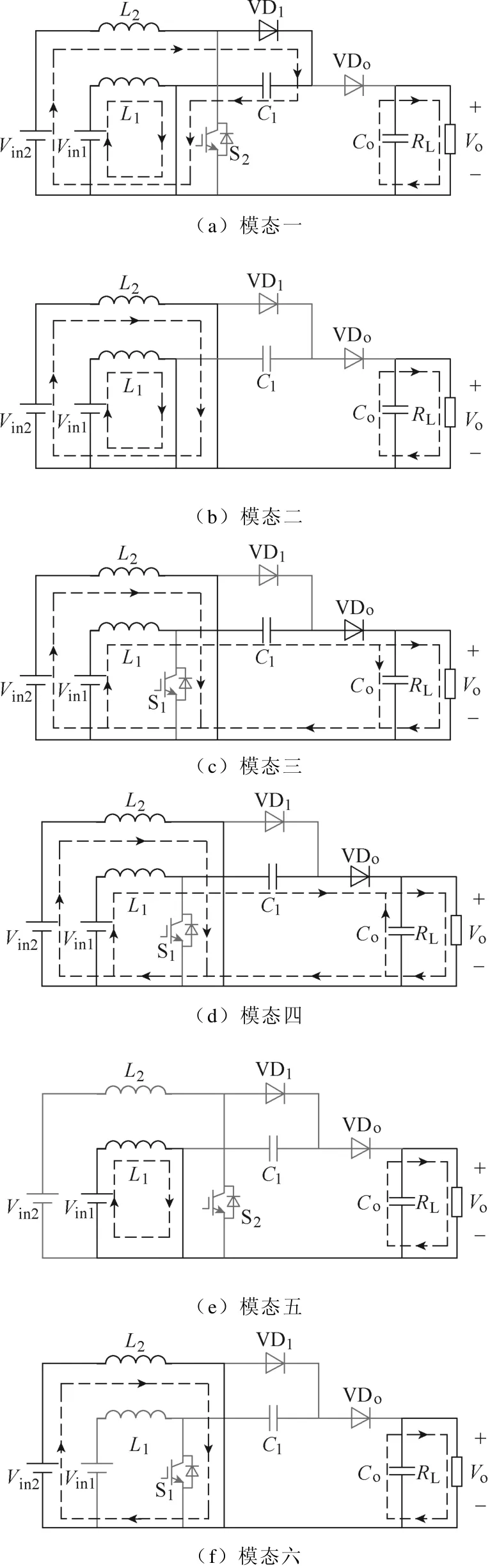
图2 不同工作模态的等效电路Fig.2 Equivalent circuit of different working modes

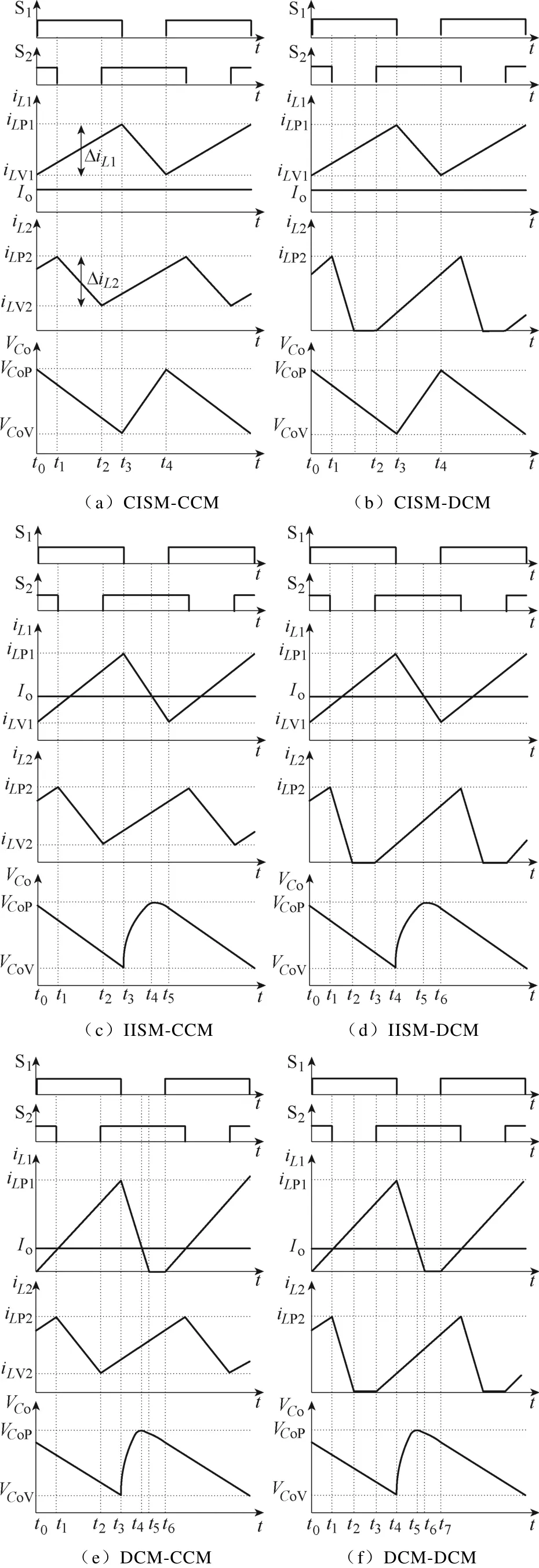
图3 电感电流与电容电压波形Fig.3 Inductor current and capacitor voltage waveforms

1.1 电感L1工作于CCM时的能量传输模式

电感L1工作于CCM时，根据电感L1的最小电流ILV1与负载电流Io之间的大小关系，可将 CCM再分为 CISM 和不完全电感供能模式（IncompleteInductor Supplying Mode, IISM）；根据电感L2的最小电流ILV2是否下降到零，可将L2的工作模式分为CCM和电流断续模式（Discontinuous Current Mode,DCM）[19]。故电感L1工作于CCM时，存在CISM-CCM（L1工作在 CISM，L2工作在 CCM）、CISMDCM、IISM-CCM和IISM-DCM四种供能模式，下面进行具体分析。

当双输入Boost变换器工作于CISM-CCM时，工作波形如图3a所示，图中ILP1为电感L1的最大电感电流，ILP2为电感L2的最大电感电流。此时电感电流满足：ILV1＞Io、ILV2＞0。在t1～t2时间段内电路工作模态如图2a所示，L2向电容C1供能，Vin1向电感L1供能；t2～t3时间段内电路工作模态如图2b所示，开关管S2闭合，Vin2开始向电感L2供能；t3～t4时间段，工作模态如图2c所示，L1同时向负载RL和电容Co供能。

当变换器工作于CISM-DCM时，工作波形如图3b所示，此时电感电流满足：ILV1＞Io、ILV2=0。电感L1的能量传输模式与变换器工作于 CISM-CCM时相同；电感L2在t1～t2时间段内向电容C1供能，t2时刻，ILV2=0，在t2～t3时间段电路工作模态如图2e所示，L2不再向电容C1供能。

当变换器工作于IISM-CCM时，工作波形如图3c所示，此时电感电流满足：Io＞ILV1＞0、ILV2＞0。电感L2的能量传输模式与变换器工作于 CISMCCM时相同；在t4时刻之前，电感L1的能量传输模式与变换器工作于CISM-CCM时相同，t4时刻，ILV1=Io，L1不再为电容Co供能，t4～t5时间段内电路工作模态如图2d所示，L1和Co同时向负载RL供能。

当变换器工作于IISM-DCM时，工作波形如图3d所示，此时电感电流满足：Io＞ILV1＞0、ILV2=0。电感L1的能量传输模式与变换器工作于IISM-CCM时相同；电感L2的能量传输模式与变换器工作于CISM-DCM时相同。

1.2 电感L1工作于DCM时的能量传输模式

当电感L1的最小电流ILV1=0时，电感L1工作于 DCM[19]，此时变换器存在 DCM-CCM（L1工作于DCM，L2工作于CCM）和DCM-DCM两种供能模式。

当变换器工作于DCM-CCM时，工作波形如图3e所示，此时电感电流满足：ILV1=0、ILV2＞0。在t5时刻之前，电感L1的能量传输模式与变换器工作于 IISM-CCM 时相同，t5时刻，ILV1=0，t5～t6时间段，工作模态如图2f所示，Co单独向负载RL供能。

当变换器工作于DCM-DCM时，工作波形如图3f所示，此时电感电流满足，ILV1=0、ILV2=0。电感L1的能量传输模式与变换器工作于DCM-CCM时相同；电感L2的能量传输模式与变换器工作于CCMDCM时相同。

2 稳态关系

2.1 CCM 稳态关系

由状态空间平均法求得电容C1两端电压VC1和输出电压Vo分别为

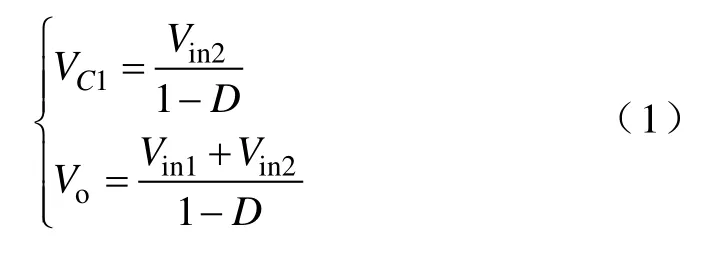
同理可求得，流过电感L1的平均电流IL1和流过电感L2的平均电流IL2间的关系为

令IL1=IL2=IL，由功率守恒可得

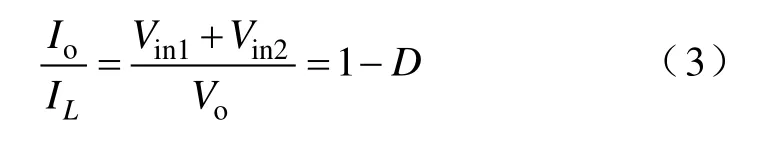
分析图3a可知，电感L1的峰值电流大小为

式中，ΔiL1为电感L1的电流变化量，

联立式（2）～式（4）可得

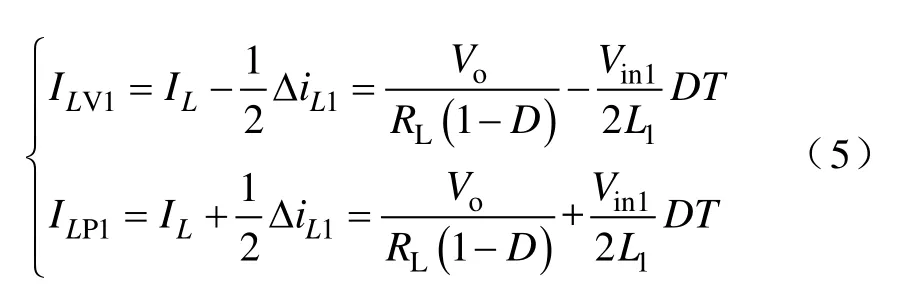
同理可得电感L2的电流变化量ΔiL2为

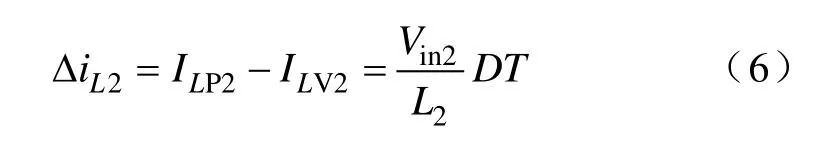
联立式（2）、式（3）和式（6）可得

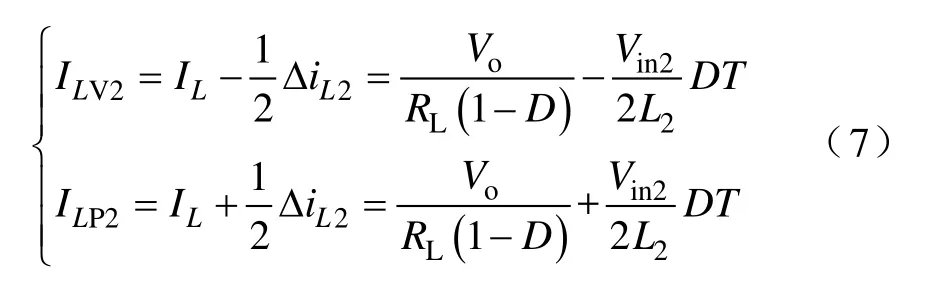
分析式（5）和式（7）可知，IL随着RL的增大而减小，ILV随着电感L的增大而增大，ILP随着电感L的增大而减小。

2.2 DCM 稳态关系

分析图3f可知，电感L1和L2都工作于 DCM时的峰值电流大小为

根据状态空间平均法，可求得变换器工作于DCM时的VC1和Vo分别为

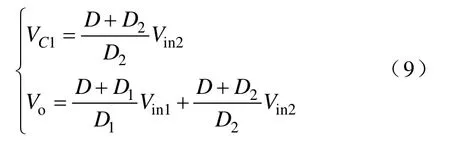
其中

式（9）中，当L1工作在 CCM 时，D1=1−D；当L2工作在CCM时，D2=1−D。

3 临界电感分析

3.1 电感L1工作于CISM与IISM的临界电感

当L1工作于CISM与IISM的临界状态时，满足ILV1=Io，令式（5）中ILV1=Io，可得 CISM与 IISM的临界电感Lk为

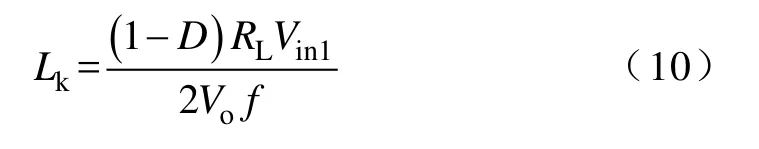
当L1＞Lk时，L1工作于CISM，如图3a所示，整个S1关断期间，L1都向电容Co和负载供能。

3.2 电感L1工作于CCM与DCM的临界电感

当L1工作于CCM与DCM的临界状态时，满足ILV1=0，令式（5）中ILV1=0，可得CCM与DCM的临界电感Lc1为

当Lk＞L1＞Lc1时，L1工作于IISM，如图3c所示，S1关断期间，当电感电流IL1=Io时，L1将不再为电容Co供能，Co开始和L1一起向负载供能；Lc1＞L1时，L1工作于DCM，如图3e所示，IL1=0时，电容Co单独向负载供能。

3.3 电感L2工作于CCM与DCM的临界电感

由于电感L2不直接对负载供能，故不存在CISM和IISM两种模式。当L2工作于CCM与DCM的临界状态时，满足ILV2=0，令式（7）中ILV2=0，可得CCM与DCM的临界电感Lc2为

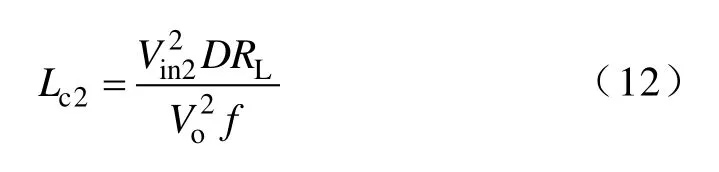
当L2＞Lc2时，L2工作于CCM，整个S2关断期间，L2都向电容C1供能；当Lc2＞L2时，如图3b所示，S2关断期间，当IL2=0时，L2不再为电容C1供能。

分析式（10）～式（12）可知，当电感L1和L2取不同值时，变换器存在六种供能模式，供能模式与电感之间的关系如图4所示。

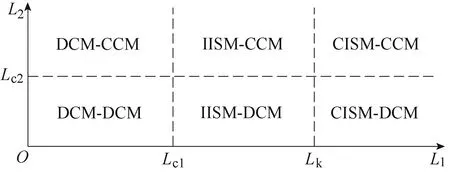
图4 供能模式与电感之间的关系Fig.4 The relationship between energy supply mode and inductance

4 输出纹波电压分析

变换器输出纹波电压可表示为

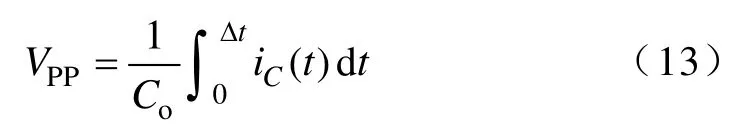
4.1 电感L1工作在CISM时的输出纹波电压分析

当变换器工作于CISM-CCM时，分析图3a可知，此时电容Co的充电时间Δt1为

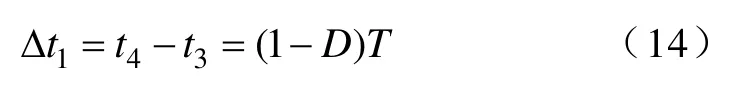
电容Co的充电电流iC(t)为

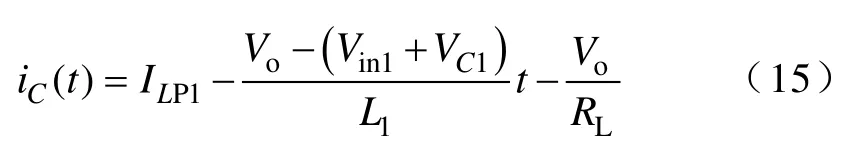
将式（1）、式（5）、式（14）和式（15）代入式（13）可得，此模式下输出纹波电压VPP1为

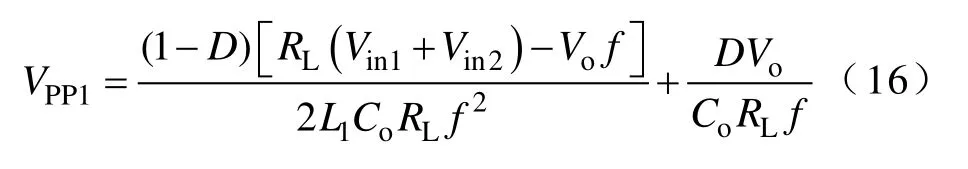
分析式（16）可知，通常满足

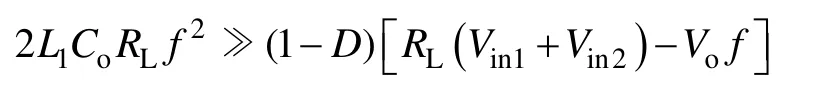
因此式（16）化简可得

当变换器工作于CISM-DCM时，输出纹波电压波形如图3b所示，将式（5）、式（9）、式（14）和式（15）代入式（13）可得，输出纹波电压VPP2为

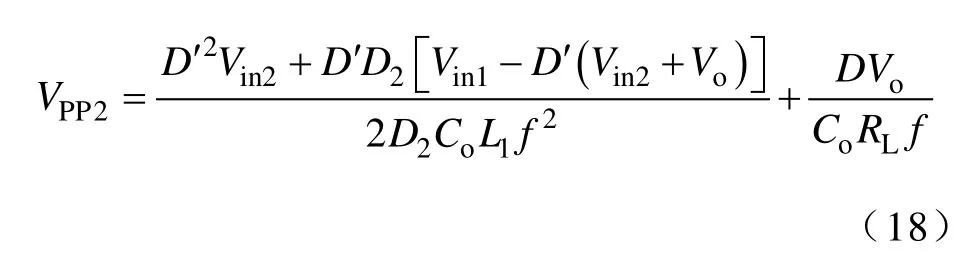
式中，D′=1−D。

分析式（18）可知，通常满足

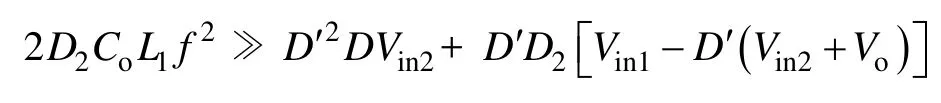
因此，式（18）化简可得

分析式（17）可知，当变换器工作于CISM-CCM时，输出纹波电压大小与电感L1和L2无关；分析式（9）和式（19）可知，当变换器工作于CISM-DCM时，VPP2随着L2的增大而减小。

4.2 电感L1工作于IISM时的输出纹波电压分析

当变换器工作于IISM-CCM时，输出纹波电压波形如图3c所示，令式（15）中iC(t)=0，即iL1(t)=Io，若设定t3=0，可得电容Co的充电时间Δt2为

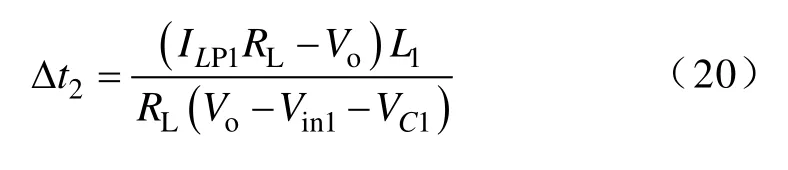
将式（1）、式（5）、式（15）和式（20）代入式（13）可得，输出纹波电压VPP3为

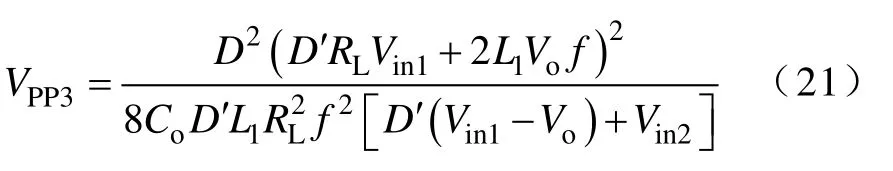
将式（21）分别对L1和RL求偏导可得

当变换器工作于IISM-DCM时，输出纹波电压波形如图3d所示，将式（5）、式（9）、式（15）和式（20）代入式（13）可得，输出纹波电压VPP4为

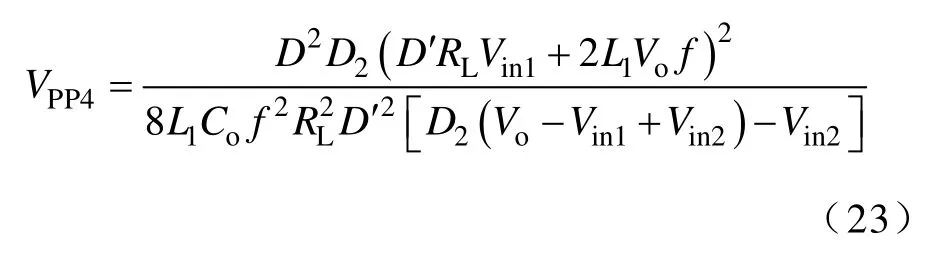
将式（23）分别对L1和RL求偏导可得

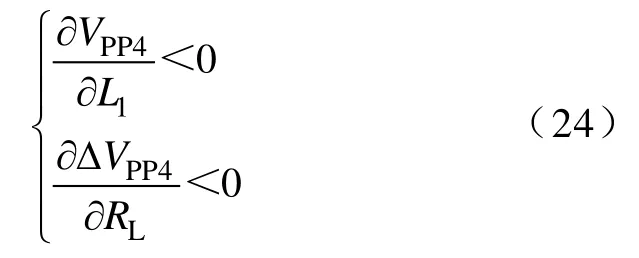
分析式（22）和式（24）可知，当电感L1工作于IISM时，输出纹波电压随着电感L1的增大而减小，随着负载RL的增大而减小。

4.3 电感L1工作于DCM时的输出纹波电压分析

当变换器工作于DCM-CCM时，输出纹波电压波形如图3e所示，根据式（15）可求得电容充电时间Δt3为

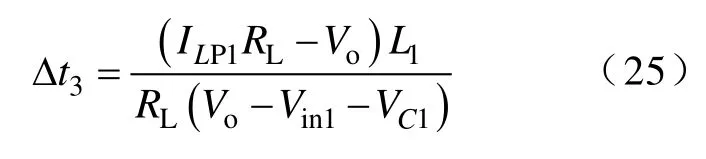
将式（8）、式（9）、式（15）和式（25）代入式（13）可得，输出纹波电压VPP5为

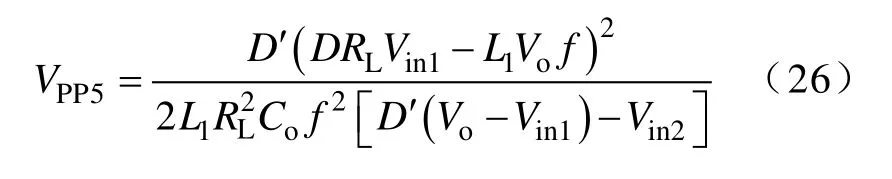
将式（26）分别对L1和RL求偏导可得

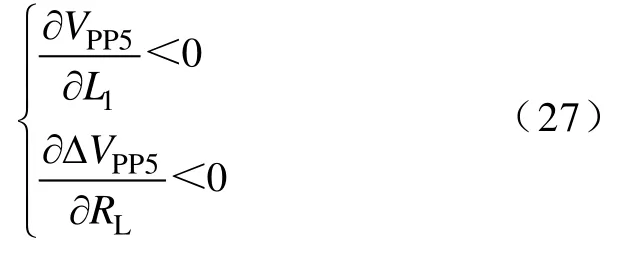
当变换器工作于DCM-DCM时，输出纹波电压波形如图3f所示，将式（8）、式（9）、式（15）和式（25）代入式（13）可得输出纹波电压VPP6为

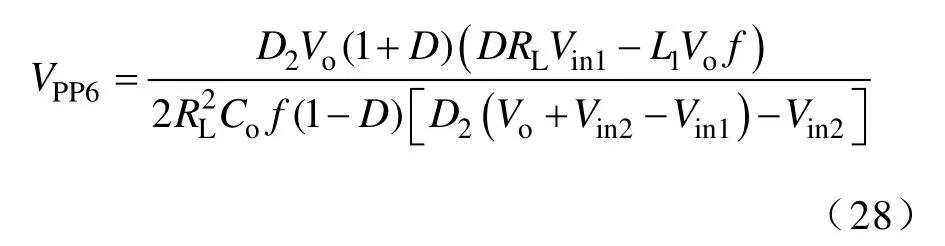
将式（28）分别对L1和RL求偏导可得

分析式（27）和式（29）可知，当电感L1工作于DCM时，输出纹波电压随着电感L1增大而减小，随着负载RL的增大而减小。

根据以上分析可得，双输入 Boost变换器输出纹波电压与电感之间的关系如图5所示。

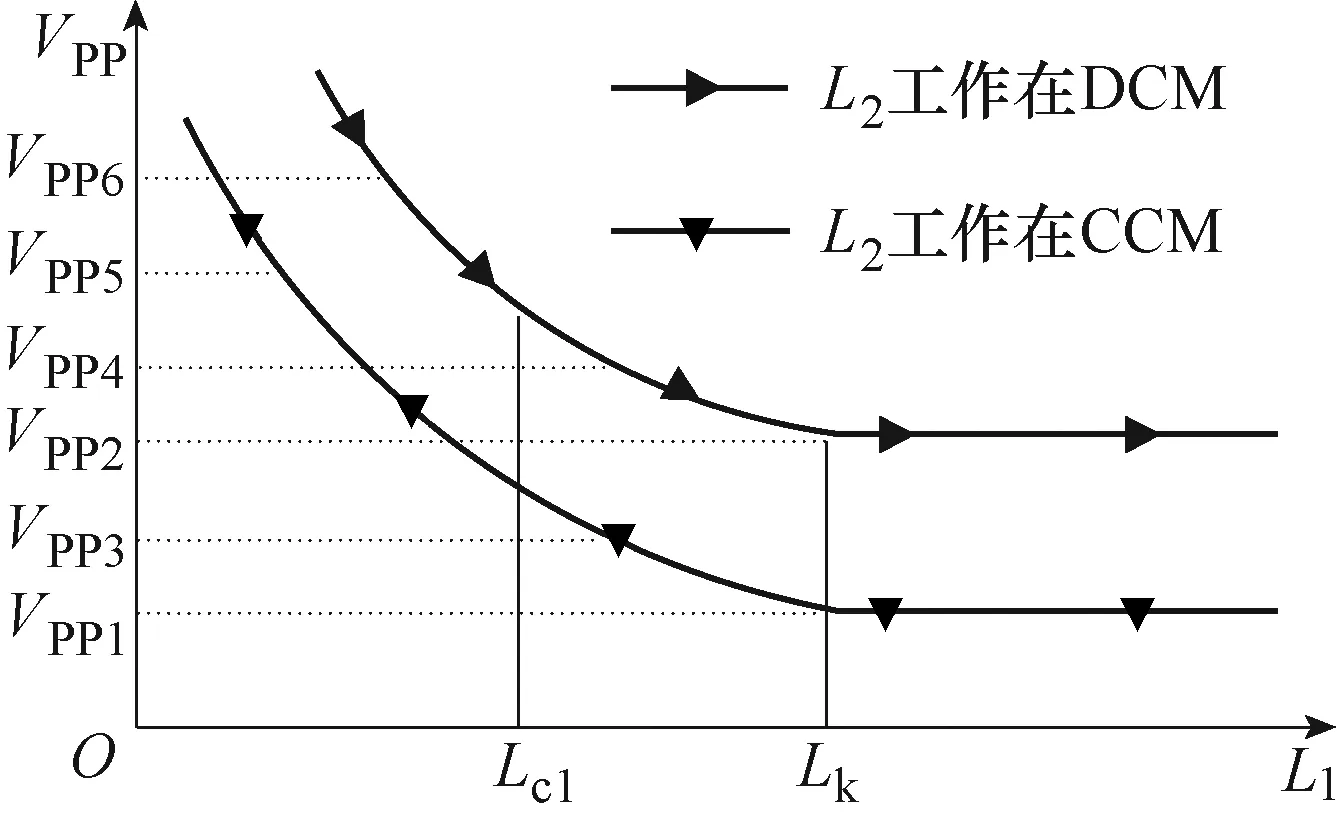
图5 输出纹波电压与电感之间的关系Fig.5 Relationship between output ripple voltage and inductance

5 多输入Boost变换器分析

多输入Boost变换器拓扑如图6所示[13]。

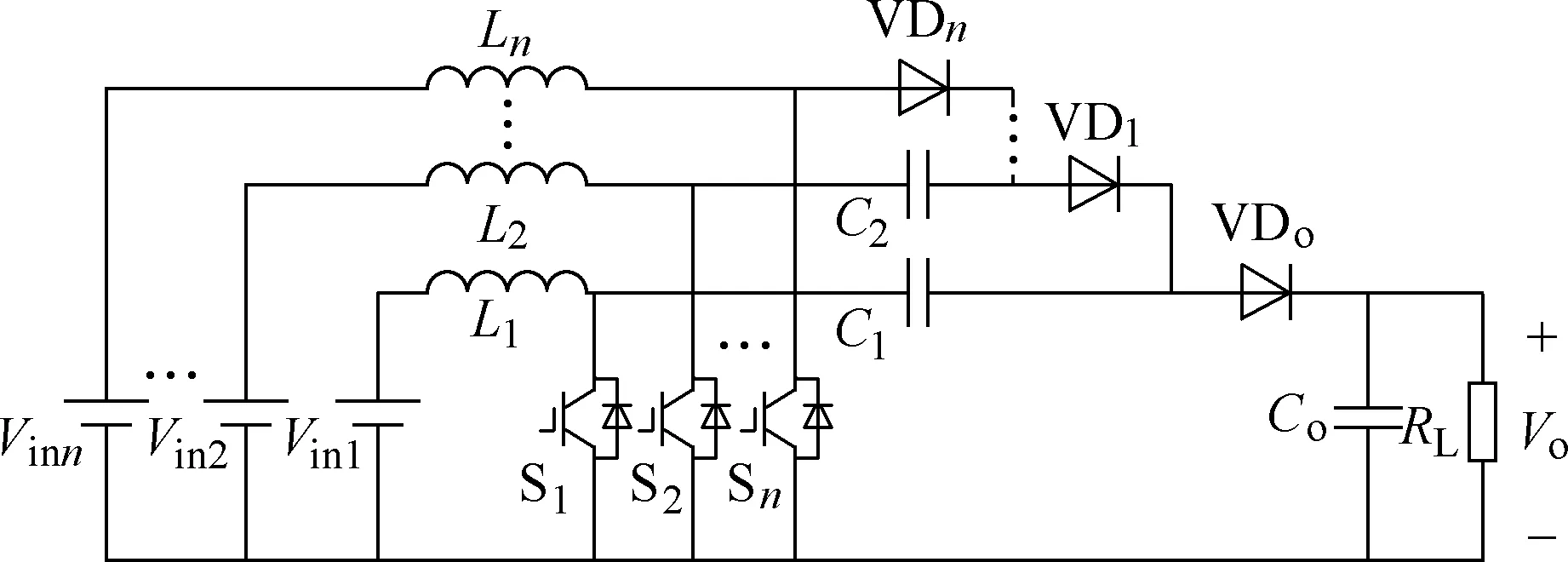
图6 多输入Boost变换器Fig.6 Multi-input Boost converter

5.1 多输入Boost变换器供能模式分析

由第3节可知，在双输入Boost变换器中，电感L1直接对负载供能，故L1存在 CISM、IISM 和DCM三种供能模式，电感L2不能直接对负载供能，故只存在CCM和DCM两种供能模式，据此可得多输入Boost变换器供能模式如图7所示。

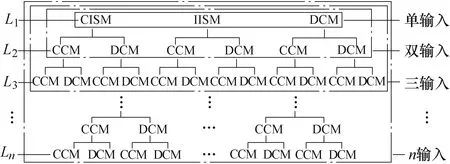
图7 多输入Boost变换器供能模式Fig.7 Energy supply mode of multi-input Boost converter

分析图7可知，当变换器为单输入时，存在CISM、IISM和DCM 3种供能模式；当变换器为双输入时，存在CISM-CCM、CISM-DCM等6种供能模式；当变换器为三输入时，存在 CISM-CCMCCM、CISM-CCM-DCM、CISM-DCM-CCM、CISMDCM-DCM等 12种供能模式；当变换器输入电源个数为n时，将存在 3 × 2n−1种供能模式。

5.2 多输入Boost变换器输出纹波电压分析

由文献[13]可知，n路输入时电容C1两端电压为

输出电压表达式为

多输入 Boost变换器电感L1工作于CISM，其余电感工作于 CCM 时，联立式（5）、式（13）～式（15）、式（30）和式（31）可得，n路输入的输出纹波电压通式为

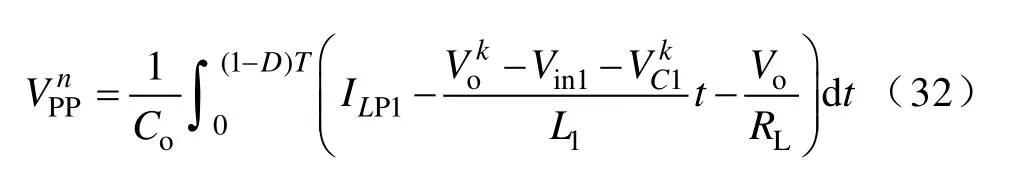
当各输入电源大小取相同值时，可得输出纹波电压为

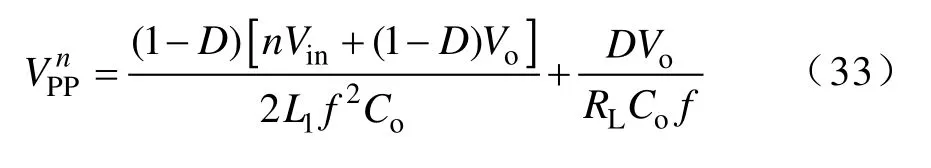
分析式（33）可知，多输入 Boost变换器工作于该模式时，其输出纹波电压大小与双输入类似，其Co越大、f越高、RL越大，输出纹波电压就越小。由于多输入变换器引入了一个新的度量n，当n取不同值时，对输出纹波电压大小将存在影响。在其他参数确定，仅改变输入电源个数时，可得输出纹波电压与输入电源个数之间的关系如图8所示。

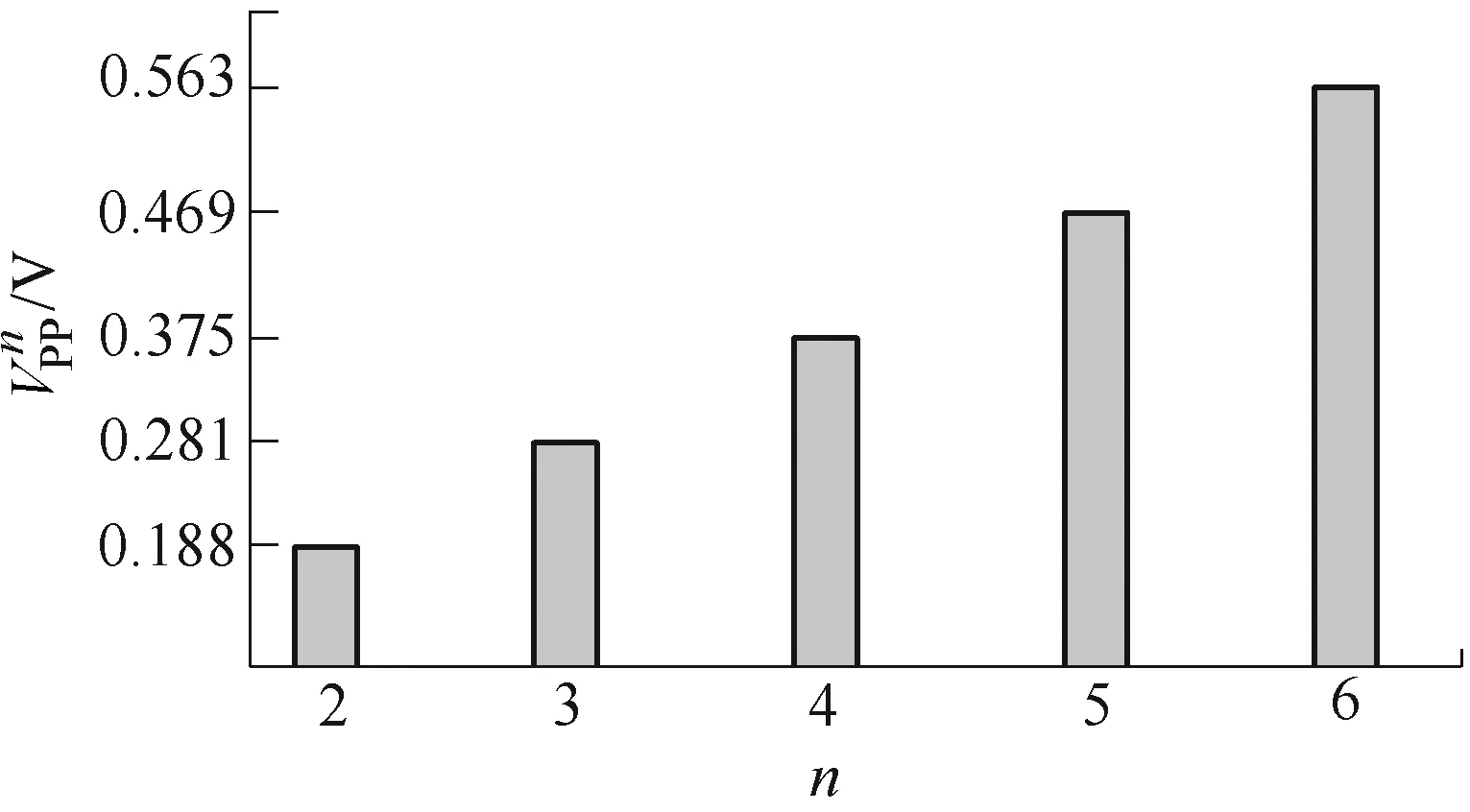
图8 输出纹波电压与输入电源个数之间的关系Fig.8 Relationship between output ripple voltage and number of input power supply

当多输入 Boost变换器工作于其他模式时，输出纹波电压分析过程与CISM-CCM时类似，限于篇幅，在此不再赘述。

6 变换器参数设计

6.1 电感设计

电感设计须满足电感电流纹波要求，若限定最大电感电流纹波为ΔiL，由式（4）和式（6）可知，满足电感电流纹波要求时的最小电感分别为

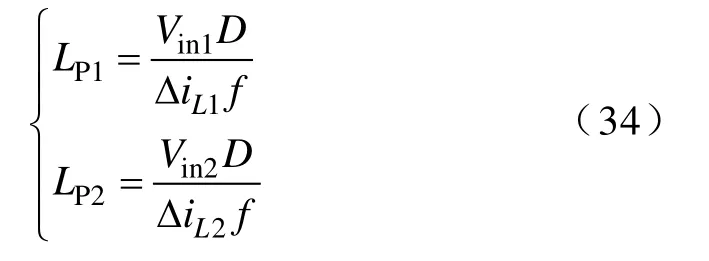
由式（11）和式（12）可知，双输入 Boost变换器CCM和DCM的临界电感Lc与Vin和RL有关，将式（11）和式（12）分别对Vin和RL求偏导可得

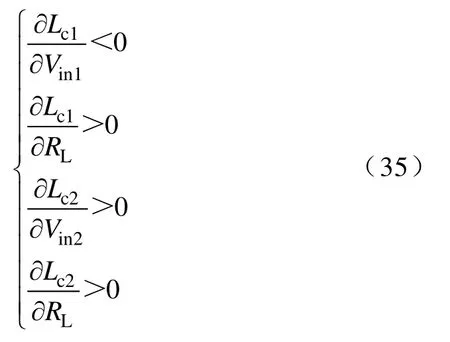
当变换器输入电压范围为[Vin1,min,Vin1,max]和[Vin2,min,Vin2,max]，负载电阻范围为[RL,min,RL,max]时，根据式（11）、式（12）和式（35）可得在动态范围内的最小电感为

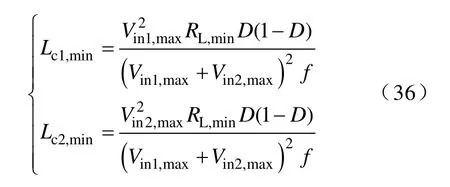
对比式（34）和式（36）可得，满足电流纹波要求和供能模式要求的最小感L1,min和L2,min分别为

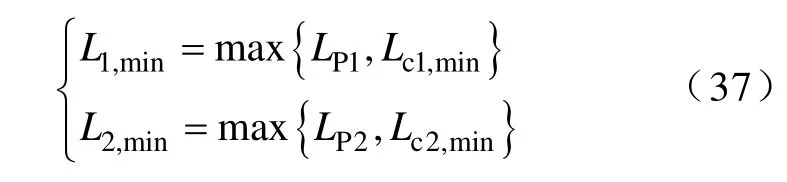
6.2 电容设计

由文献[19]可知，电感确定的变换器最大输出纹波电压如式（17）所示，分析式（17）可知，输出纹波电压大小与Vin1、Vin2和RL有关，将VPP1分别对Vin1、Vin2和RL求偏导可得

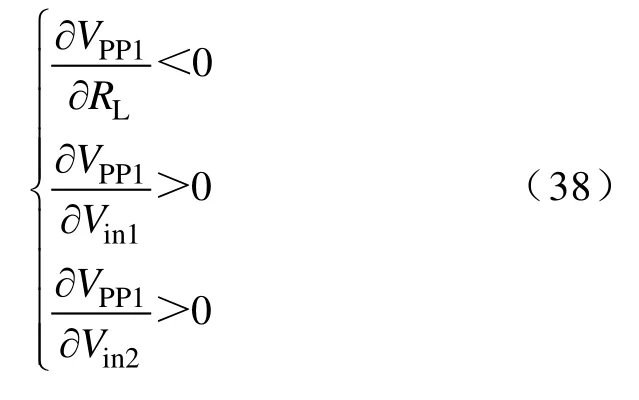
分析式（17）和式（38）可知，在输入电压和负载电阻动态范围内，可得最大输出纹波电压为

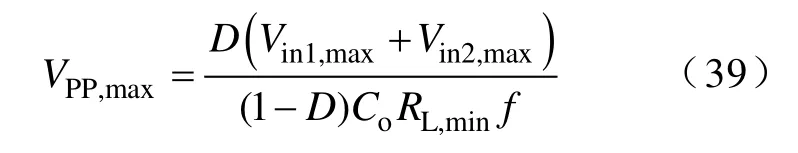
若限定最大输出纹波电压为VPP,max，可得满足输出纹波电压要求的最小电容为

7 实验验证

为了验证理论分析的正确性，对双输入 Boost变换器进行实验分析，双输入 Boost变换器电路参数见表1。

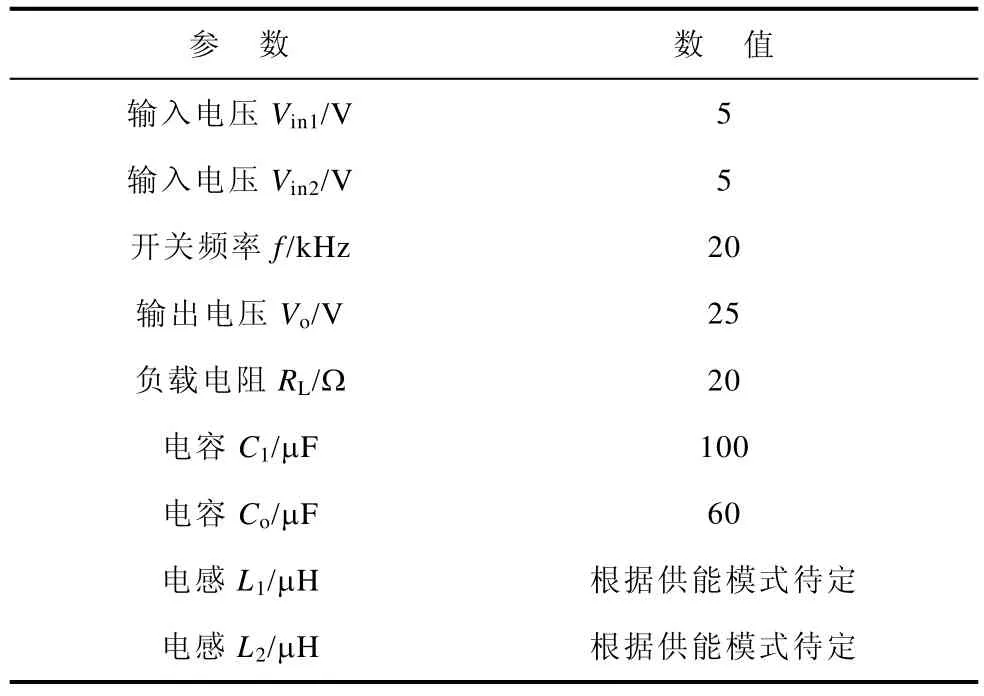
表1 双输入Boost变换器电路参数Tab.1 Dual input Boost converter circuit parameters

将表1中的参数代入式（10）～式（12）中可得，临界电感Lk=40μH、Lc1=24μH、Lc2=24μH。实验中电感L1分别取 212μH、30μH 和 12μH，电感L2分别取 212μH和 12μH，电感电流和电容电压实验波形如图9所示，实验所得输出纹波电压数据见表2和表3，其输出纹波电压标幺值定义ΔV=VPP/Vo。

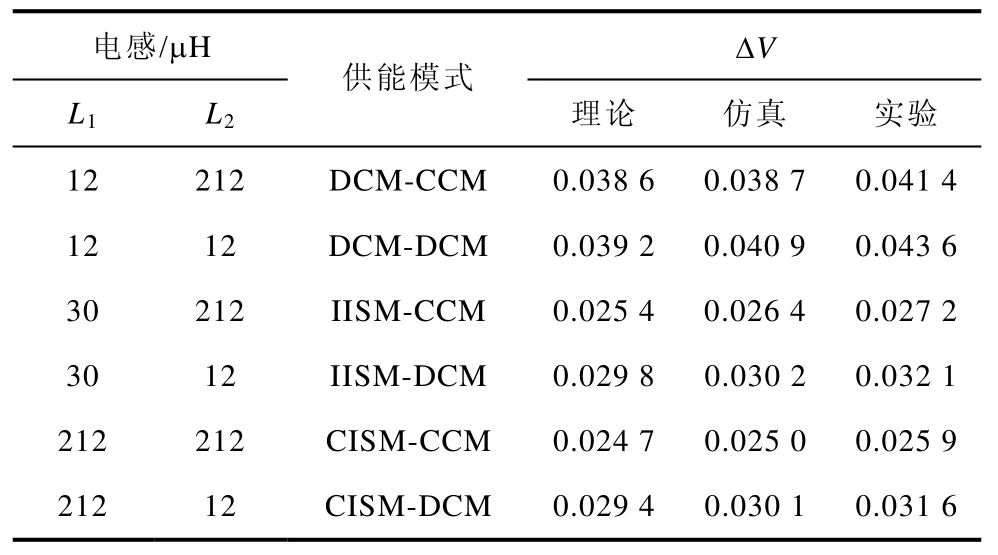
表2 供能模式与输出纹波电压Tab.2 Energy supply mode and output ripple voltage

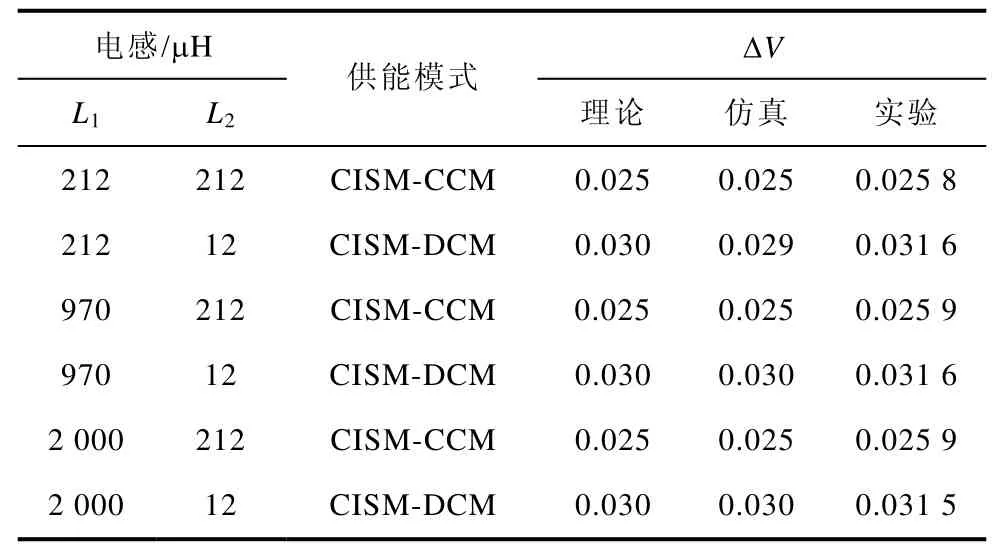
表3 不同电感对输出纹波电压的影响Tab.3 Influence of different inductors on output ripple voltage

分析图9a～图9f可看出，L1=L2=212μH时，ILV1、ILV2均大于 0，且ILV1＞Io，变换器工作于 CISMCCM；L1=212μH、L2=12μH时，存在ILV2=0，变换器工作于CISM-DCM；L1=30μH、L2=212μH时，存在Io＞ILV1＞0，变换器工作于 IISM-CCM；L1=30μH、L2=12μH时，变换器工作于IISM-DCM；L1=12μH、L2=212μH时，存在ILV1=0，变换器工作于DCM-CCM；L1=L2=12μH 时，变换器工作于 DCM-DCM。分析图9c～图9f可知，当IL1=Io时，电感L1不再对电容Co供能，Co开始和L1一起向负载供能，VPP开始减小，当IL1=0时，由电容Co单独向负载供能，直到下一周期。

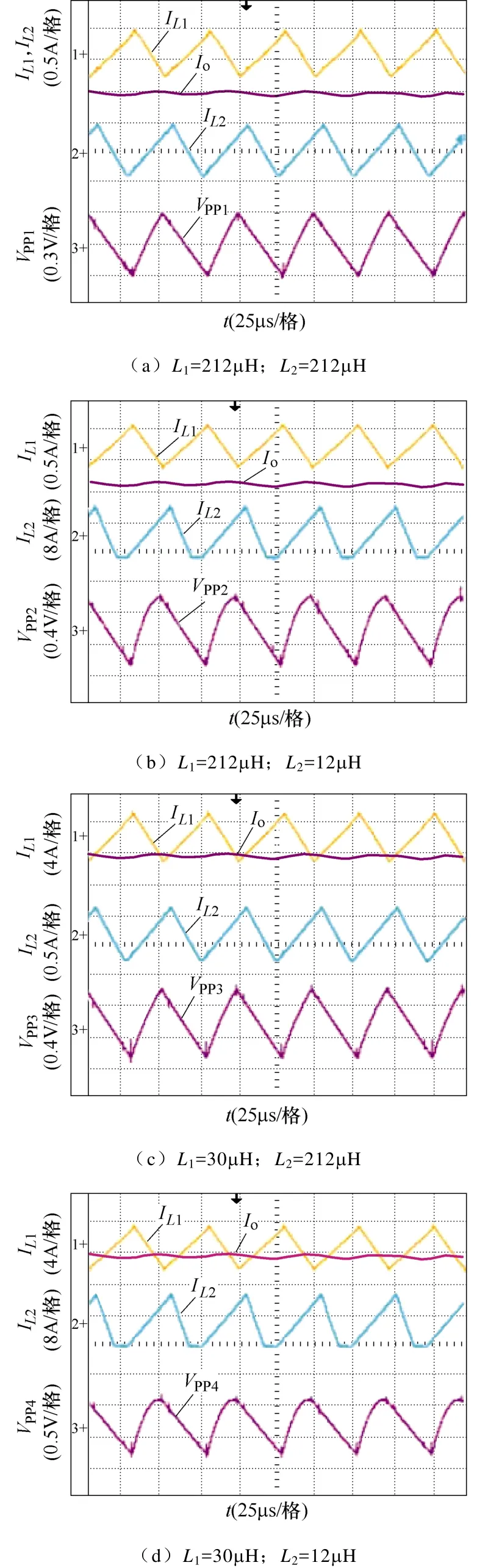
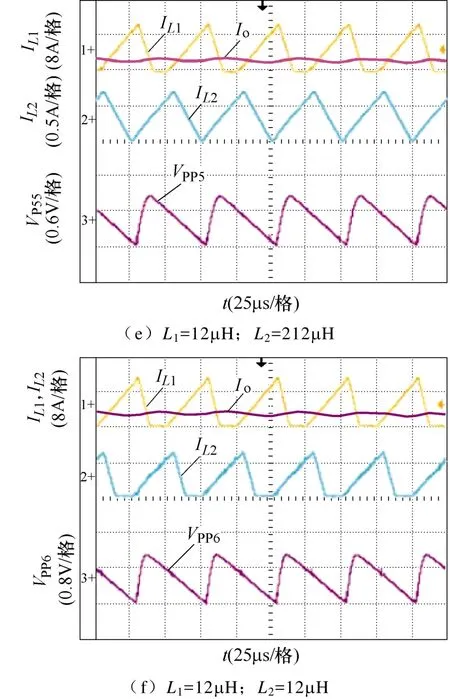
图9 电感电流和电容电压实验波形Fig.9 Experimental waveforms of inductance current and capacitance voltage

供能模式与输出纹波电压见表2。分析表2可知，输出纹波电压随着电感的增大而减小，当变换器工作于CISM-CCM时输出纹波电压最小。不同电感对输出纹波电压的影响见表3。由表3可知，此时变换器分别工作于 CISM-CCM和 CISM-DCM；增大L1的取值，输出纹波电压大小不变；而当L1大小不变时，输出纹波电压随着L2的增大减小。实验结果与理论分析结果十分接近，验证了理论分析的正确性。

下面对双输入 Boost变换器参数设计方法进行实验验证，具体参数为：输入电压范围Vin1=5～10V、Vin2=5～10V，负载电阻范围RL=10～30Ω，输出电压Vo=50V，限定最大电感电流纹波ΔiL1=10%IL1、ΔiL2=10%IL2，限定最大输出纹波电压ΔV=4%Vo，工作频率f=20kHz。根据式（37）和式（40）计算可得，L1,min=480μH，L2,min=480μH，Co,min=75μF。实验中L1和L2取 480μH，Co分别取 75μF 和 100μF。不同参数的实验波形如图10所示，实验数据见表4。

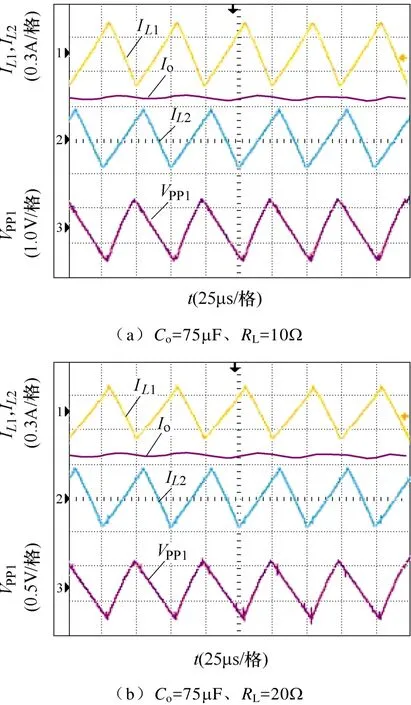
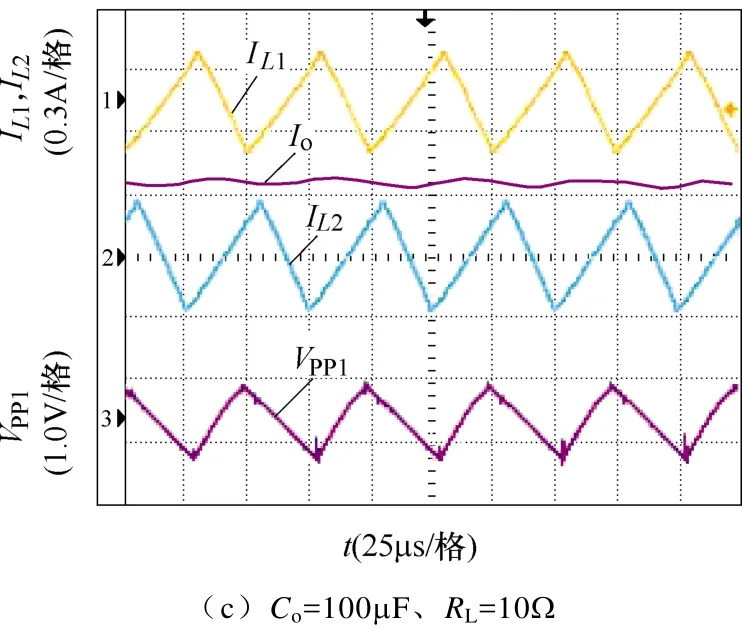
图10 不同参数的实验波形Fig.10 Experimental waveforms for different parameters

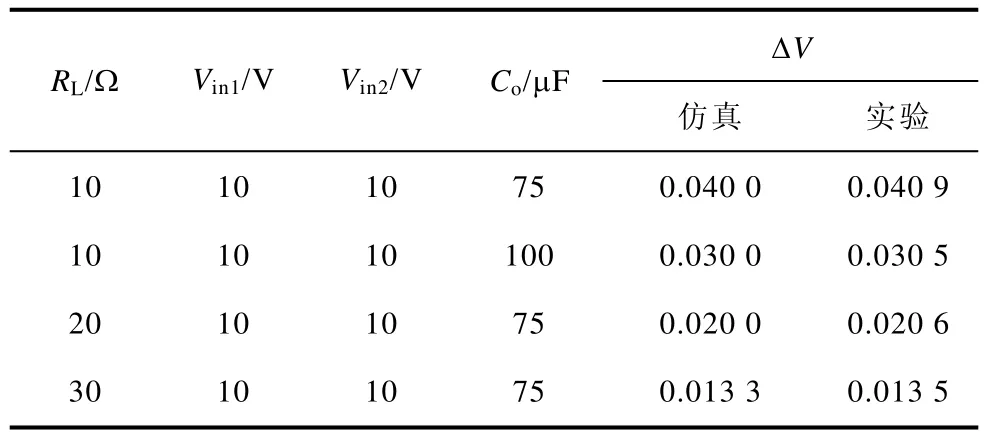
表4 不同参数对输出纹波电压的影响Tab.4 Influence of different parameters on output ripple voltage

分析图10和表4可知，当变换器参数取值为RL=RL,min、Vin1=Vin1,max、Vin2=Vin2,max、Co=Co,min时，输出纹波最大，且满足最大纹波指标要求；当Co、Vin1和Vin2不变时，输出纹波电压随着RL的增大而减小；当RL、Vin1和Vin2不变，输出纹波电压随着Co的增大而减小，故可知，Co,min是满足纹波要求的最小电容，实验结果与理论分析相一致，验证了理论分析的正确性。受元器件寄生参数影响，实验所得输出纹波电压略大于理论值，在实际应用中，在本文理论分析的基础上加入相应的裕度，即可满足供能模式和纹波电压要求。

8 结论

通过对双输入 Boost变换器的能量传输模式及输出纹波电压进行深入研究，得到如下结论：

1）双输入Boost变换器能量传输模式与电感大小密切相关，存在三个临界电感，当L1＞Lk时，电感L1工作于 CISM；当Lk＞L1＞Lc1时，电感L1工作于 IISM；当Lc1＞L1时，电感L1工作于 DCM；当L2＞Lc2时，电感L2工作于CCM；当Lc2＞L2时，电感L2工作于DCM。

2）当L1工作于 CISM时，输出纹波电压大小与L1的取值无关；当L1工作于IISM和DCM时，输出纹波电压随着L1的增大而减小；当L2工作于CCM 时，输出纹波电压大小与L2的取值无关；当L2工作于DCM时，输出纹波电压随着L2的增大而减小。

3）当变换器为单输入时，存在3种供能模式，当变换器为双输入时，存在6种供能模式，当变换器为n路输入时，存在 3 × 2n−1种供能模式。变换器的输出纹波电压大小与输入电源个数有关，且纹波电压随着输入电源个数的增多而增大。

4）通过对变换器参数进行设计，在输入电压和负载电阻动态范围内，得到了满足纹波要求的最小电感和最小电容。本文研究所得结论对于多输入Boost变换器分析和设计具有指导意义。