两极永磁电机静态内外磁场研究

饶 凡 吴旭升 高 嵬 李 达

（海军工程大学电气工程学院 武汉 430033）

0 引言

近年来，电机制造、控制技术[1-3]得到了飞速发展，伴随着更高磁能积的稀土金属永磁体（如钕铁硼）的出现[4-5]，性能优异[6-8]的中小功率永磁电机在航空航天、军事领域、民用工农业等诸多领域应用越来越广泛。在一些特殊的领域，如水下航行器、高精密伺服系统、船舶等，永磁电机等存在的外围漏磁场可能降低水下航行器、船舶的安全隐蔽性，对于高精密伺服系统，永磁电机的外围漏磁大小可能会影响周围的精密传感器等，从而产生误差。

文献[9-10]针对测磁载体的永磁电机在环境中的漏磁场对地磁测量产生明显的干扰进行研究。文献[9]针对空气中测磁的不同情况仿真，定性地得出磁场泄漏的规律，对实际工程具有一定的参考价值，但并没有量化各个量（如铁磁材料、电机本体尺寸）对泄漏磁场的影响，即缺乏数学模型；文献[10]同样也有相应仿真工作，在理论方面，只是罗列了几个电磁场公式，对电机漏磁的数学模型描述较少。

文献[11-12]对永磁直流电机分别进行二维径向漏磁与二维轴向漏磁仿真分析，测量了环境中不同半径漏磁场磁感应强度，定性地得到电机环境漏磁场的分布规律。

对永磁电机内部磁场建模已有很多文献[13-15]，但是鲜有学者对永磁电机外部环境磁场进行理论研究。文献[16-18]对两极平行充磁电机进行内部磁场建模分析，忽略定子铁心影响，得到了电机气隙、永磁体的解析模型。

本文在文献[17-18]的基础上，考虑环境漏磁，对两极平行永磁电机进行理论研究，提出了计算永磁电机内外含定子、外围环境等各个域的磁场解析模型，重点分析了永磁电机外围环境漏磁影响因素和变化规律，并利用有限元软件和实物试验进行验证。对其他电机环境磁场分析具有一定的参考意义，也为地磁测量设备的磁场补偿、外围漏磁优化提供了思路。

1 模型建立

永磁电机模型简化等效为5个区域：转轴域S（shaft）、永磁体域 P（PM）、气隙域 A（air gap）、定子铁心域I（stator iron）、环境域C（circumstance），并忽略定子齿，认为定子是规则圆环，其等效模型如图1所示。

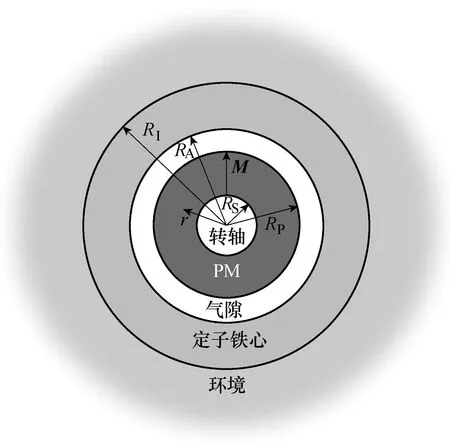
图1 电机等效模型Fig.1 Motor equivalent model

图1中，RS为转轴半径（同时为永磁体内半径），RP为永磁体外半径（同时为气隙内半径），RA为气隙外半径（同时为铁心内半径），RI为铁心外半径。

为分析其规律，将永磁体认为是两极，对于平行充磁的永磁体，其磁化强度M可以写为

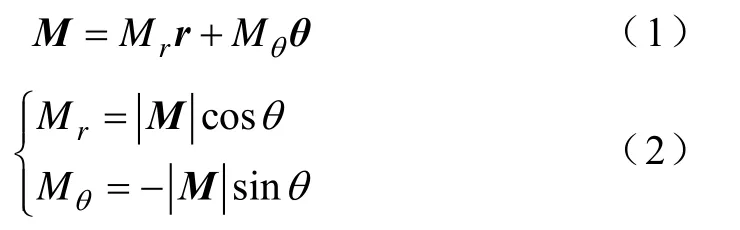
式中，Mr为永磁体的径向分量；Mθ为其周向分量。由其分量可知， ∇ ×M= 0 。对于永磁体，其矢量磁位满足泊松方程，对于铁心、空气域和环境，则满足拉普拉斯方程。

对于二维磁场，矢量磁位A没有径向分量和周向分量[18]，即：Ar=0，Aθ= 0 ，故各个域的矢量磁位A满足

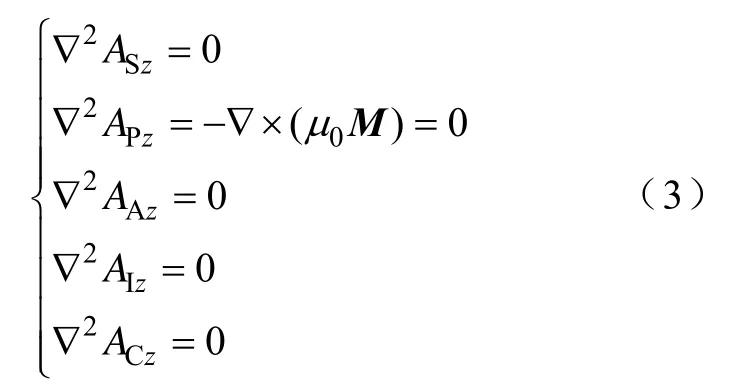
式中，Az的下标S、P、A、I、C分别为转轴域、永磁体域、气隙域、定子铁心域、环境域的矢量磁位z分量；0μ为真空磁导率。

2 模型求解

2.1 求解拉普拉斯方程

式（3）中各式均为齐次偏微分方程，故以任一域为例，可以利用分离变量法求解方程[19]。

由于圆形域利用圆柱坐标系求解更容易，故建立圆柱形坐标系，将式（3）中任一式展开，可得

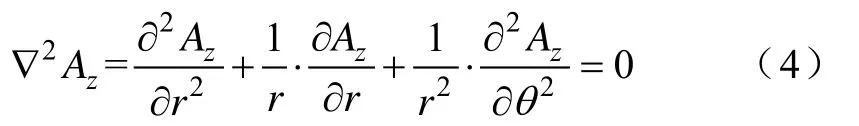
令Az=R(r)Φ(θ)，则式（4）可以变为

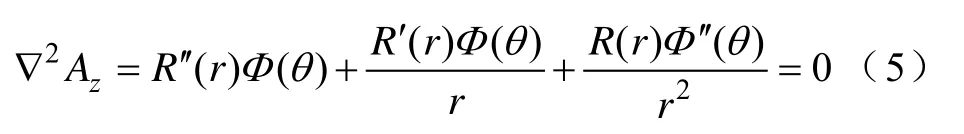
式中，R(r)、Φ()θ为分离变量法的过程量。

整理式（5），可得到两个独立方程，有

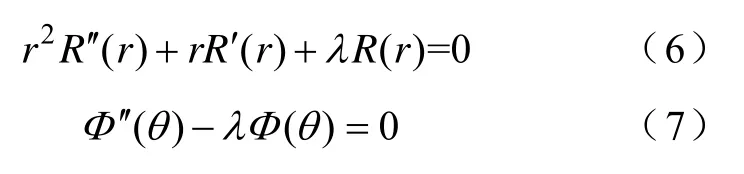
分别求解两个独立方程，可以得到矢量磁位Az的表达式为

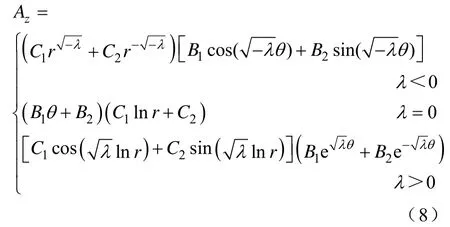
式中，B1、B2、C1、C2均为系数。

2.2 周期性与对称性条件

矢量磁位Az呈现周期性，即Az(r,θ) =Az(r,θ+ 2 π)，故有

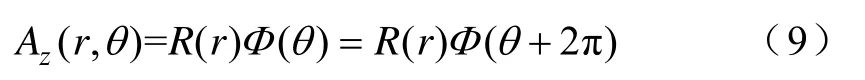
在式（8）中，对λ不同的取值对应不同的Az表达式，但是满足周期性条件的只有λ＜0，只有当为整数m时，式（9）才能成立，即λ=−m2，m= 1 ,2,3,… 。

因此，矢量磁位Az简化为

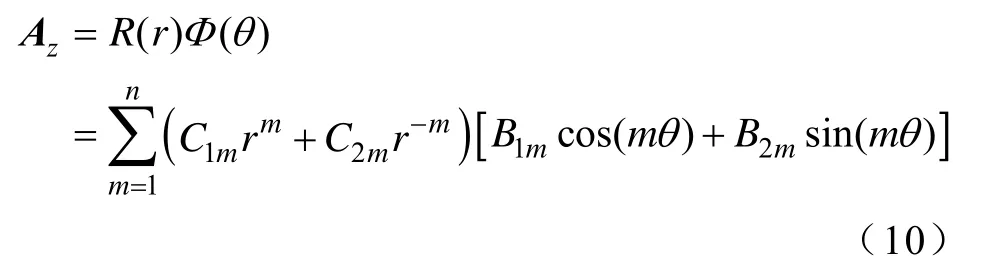
利用磁场的对称性[20]，径向分量关于机械角度θ呈偶对称，周向分量关于机械角度θ呈奇对称，即

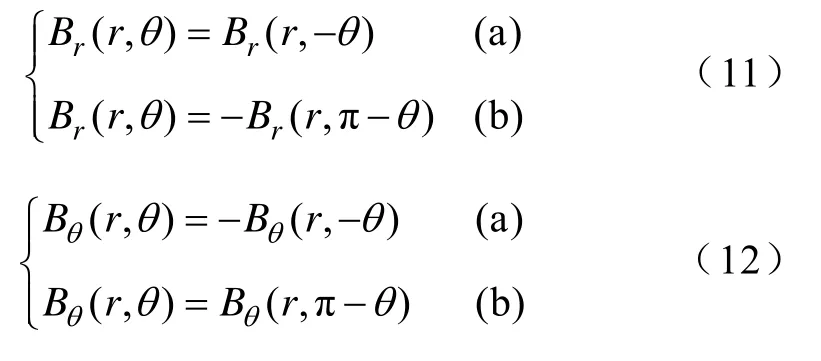
矢量磁位A与磁感应强度B的关系为B=∇×A，在极坐标下，由于在二维中，仅仅只有Az分量，B无z分量，由磁场的对称性，根据式（11a）或者式（12a）可以得到系数B1=0，根据式（11b）或者（12b）可以得到

令磁场系数D1m=mB2mC1m，D2m=mB2mC2m，磁感应强度B的周向、径向分量分别为

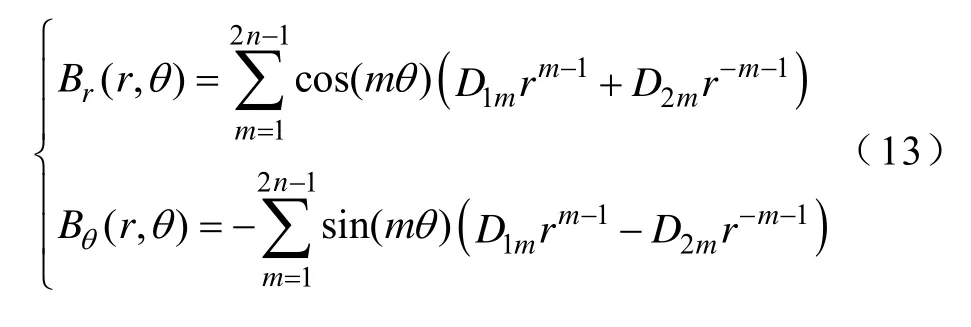
式中，n=1, 2, 3,…。

将式（13）的磁场系数D1m、D2m求出就可以确定不同域的磁感应强度表达式。

2.3 边界条件与自然条件

根据图1的永磁电机等效模型，可以知道永磁电机分5个域、4个边界（转轴与永磁体边界SP、永磁体与气隙边界PA、气隙与定子铁心AI、定子铁心与环境IC），由边界的磁场强度H的周向连续，磁感应强度B的径向连续[21]和铁心磁导率远远大于气隙磁导率，且气隙很小，可以得到4组边界条件为

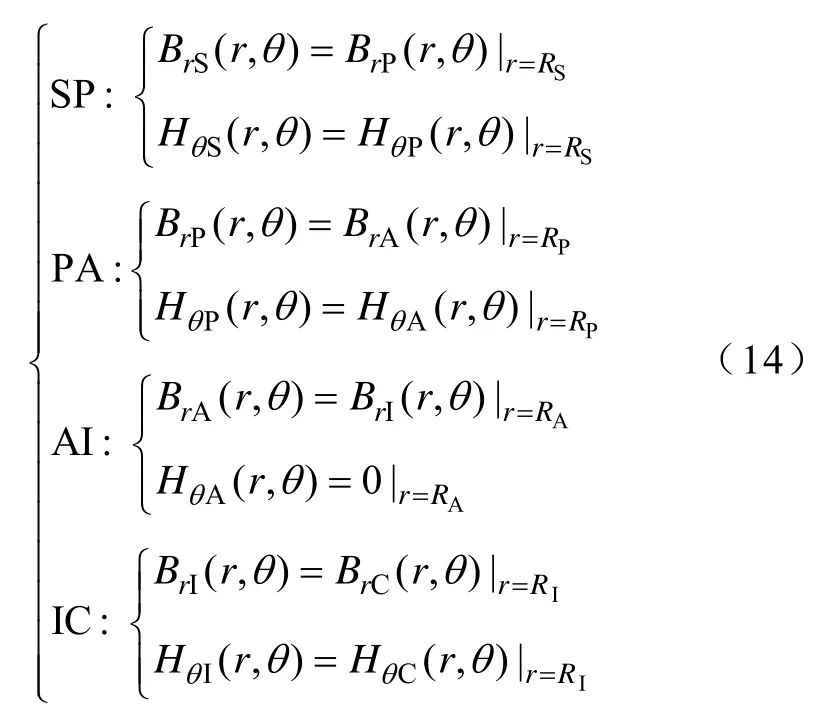
在无穷远处，即r→∞，磁感应强度为0，即

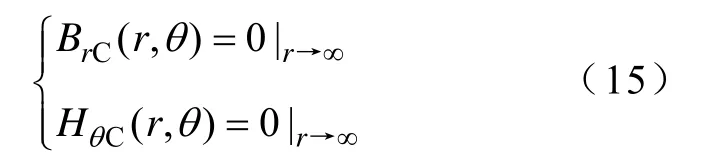
对于电机外围的环境，磁场系数DC1m=0。当r→ 0 时，矢量磁位Az为定值，故系数CS2m= 0 ，即

根据不同区域的H与B的关系[22]，可得磁场强度H的周向分量与磁感应强度B的周向分量关系为

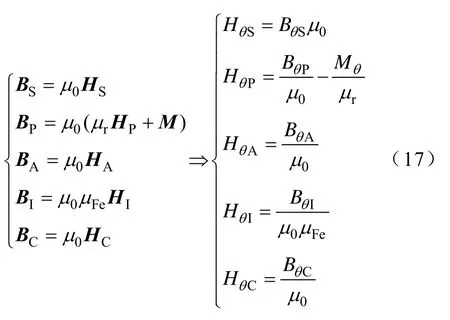
2.4 解析模型结果

将边界条件式（14）、自然条件式（15）、式（16）以及式（17）应用于式（13），如果将磁化强度周向分量Mθ也用级数表示，有

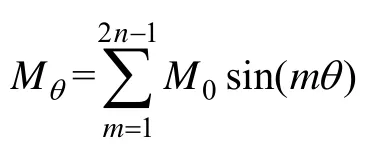
其中

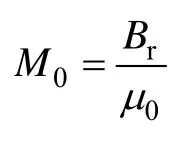
则可以得到各系数之间满足

将式（18）用矩阵形式表示为RmDm+U=0，各个域的磁场系数为

其中

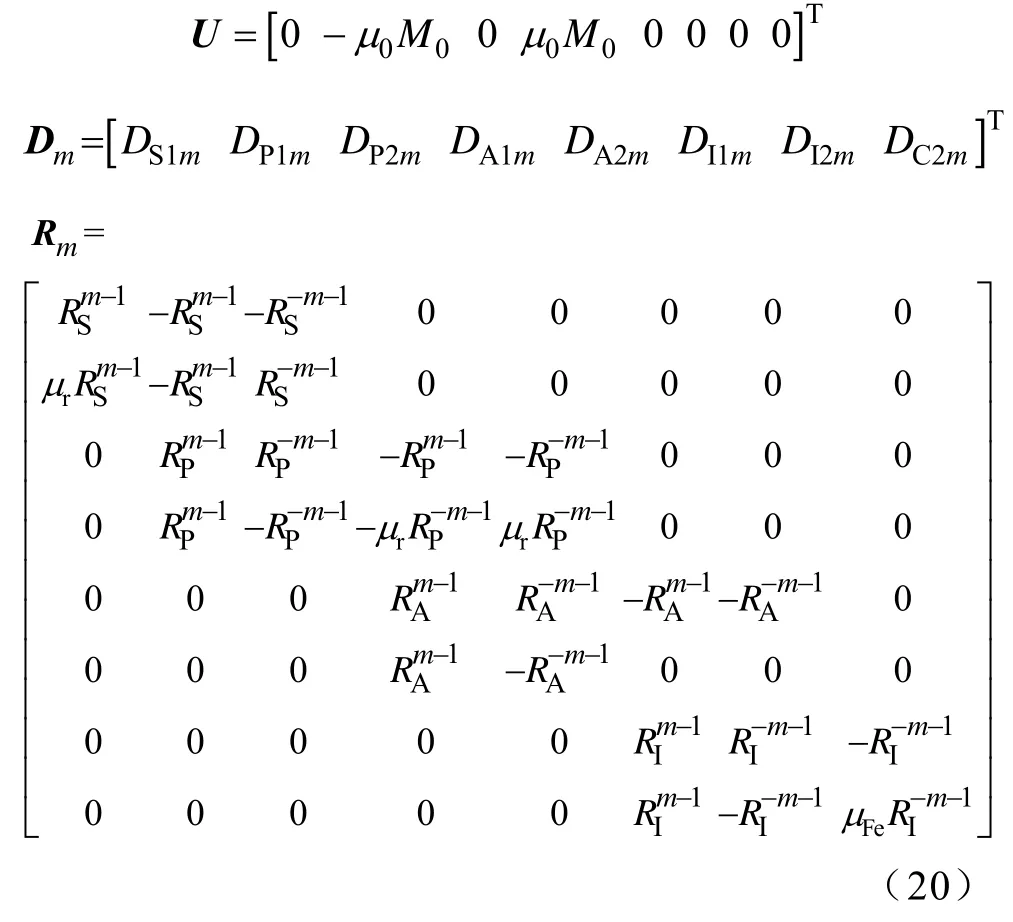
求解式（19）可以得到系数向量Dm（见附录），代入式（13）得到不同域的解析磁场径向、周向分量。从系数向量Dm可知，环境的磁感应强度系数DC2m与磁化强度M0（或剩磁Br）成正比、与铁心的相对磁导率μFe成反比，并与电机各部件尺寸（RS、RP、RA、RI）和永磁体相对磁导率μr相关。

由于工程应用中铁心饱和对电机的性能产生较大影响，同样会对电机的环境泄漏磁场产生影响。电机的气隙磁场越强，定子铁心的饱和程度越明显，即铁心的相对磁导率就越小。

考虑饱和时，铁心磁导率和铁心磁化磁场可以用μr-B曲线描述，解析模型中的磁导率可以根据铁心的工作点来确定，即气隙磁场的强度可以反映铁心工作点的相对磁导率μFe，将μFe代入附录中的磁场系数，就能得到饱和时磁场分布规律。

3 仿真分析

3.1 电机参数及解析结果

利用 Comsol仿真软件对模型进行仿真验证，其电机参数见表1。

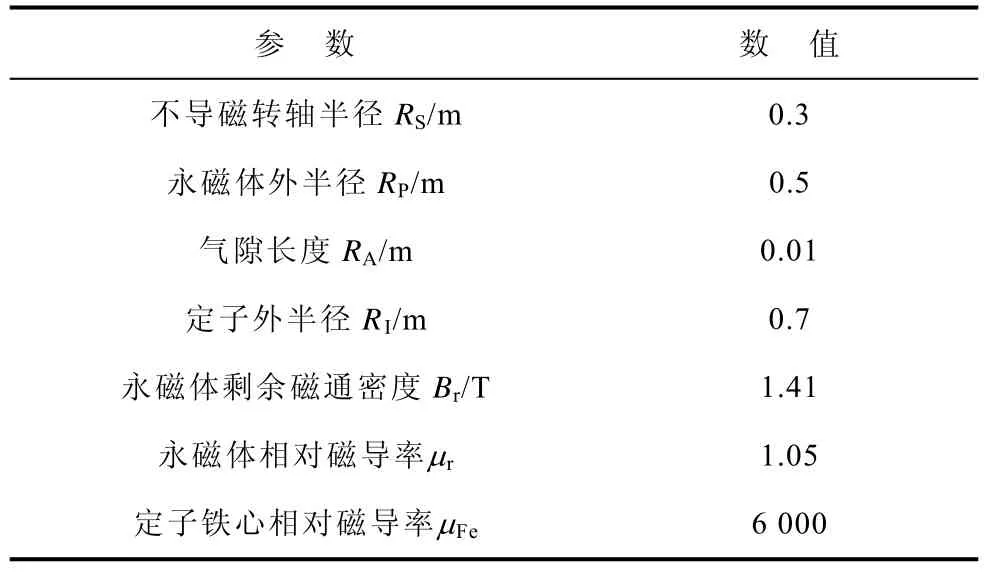
表1 电机参数Tab.1 Motor parameters

平行磁化的永磁体，其气隙磁场的径向分量与周向分量均呈现正弦分布，故取m=1，磁化强度M0=Br/μ0，结合表1的电机参数，利用附录的关系式可以计算出各个域的系数，进而得到各个域的磁场解析式为

可以看出，转轴中径向与周向磁感应强度与半径无关，环境中径向与周向磁感应强度的幅值与距离二次方成反比。

3.2 仿真结果

建立 Comsol电机模型，取磁化方向为x轴正向，永磁电机内外磁场分布如图2所示。

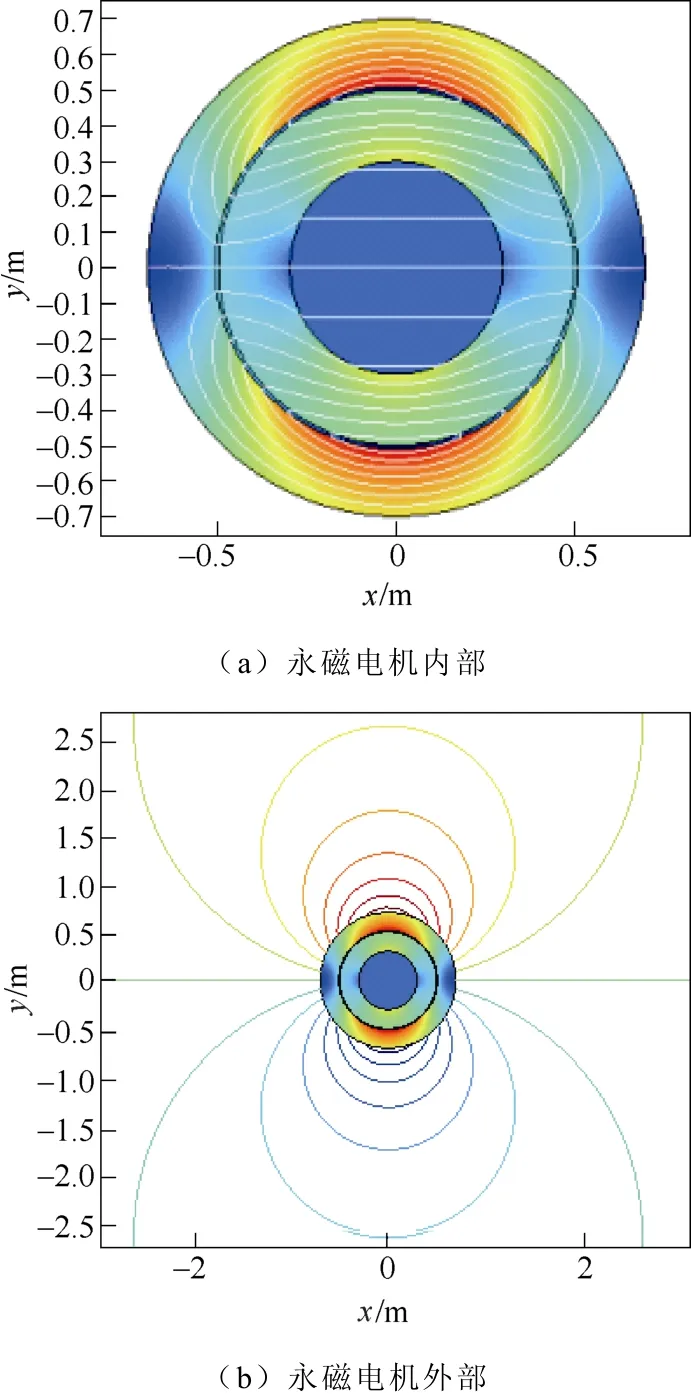
图2 永磁电机内外磁场分布Fig.2 Motor internal and external magnetic field distribution

永磁电机转轴磁场均匀分布，永磁体N极产生的磁场穿过气隙，垂直进入铁心，绝大部分磁场经过定子铁心回到S极，很少部分穿出铁心，进入环境中，但最终还是会回到S极（见图2b）。

3.2.1 永磁电机内部

转轴中的磁场取决于域系数DS1和角度θ，当角度θ不变时，即转轴内的磁感应强度为恒定值，例如取θ=0°（即和x轴方向重合），取测量位置如图3a所示，其磁感应强度随坐标变化如图3b所示。

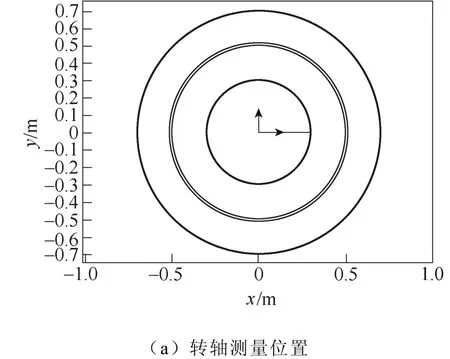
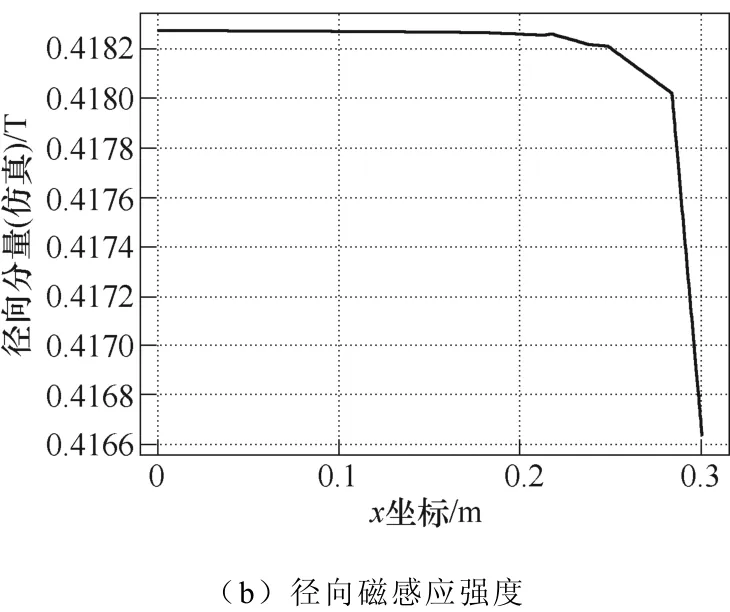
图3 转轴域径向磁感应强度Fig.3 Br (Rotary shaft)

磁感应强度模仿真值约为0.418 3，而理论值DS1=0.418 7，故相差很小，误差约为0.1%。

在电机内部不同区域设置测量圆，可以得到相应的理论与仿真值，结果如图4所示。

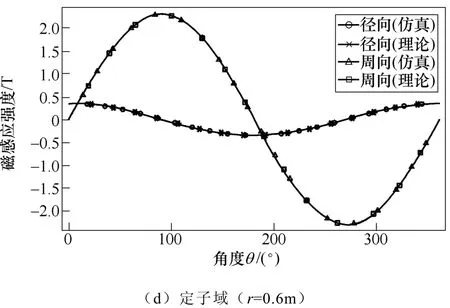
图4 不同区域周向与径向磁感应强度理论和仿真结果Fig.4 Theoretical and simulation results of Br and Bθ in different regions

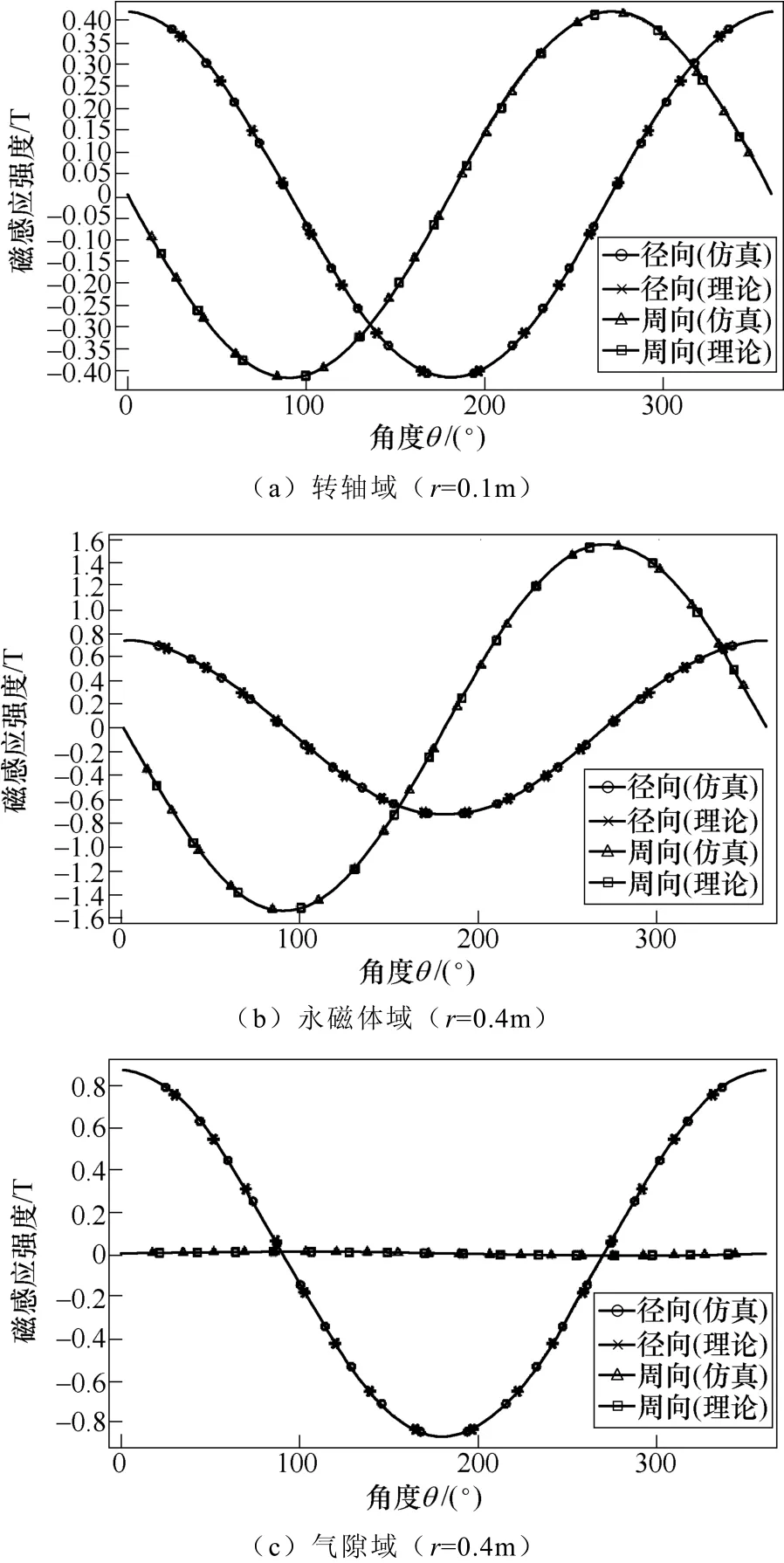
从图4可以知道，理论与仿真结果十分吻合，误差均在0.1%内。在测量圆上，各个域的周向与径向磁感应强度均呈现正弦分布，周向分量与径向分量相位相差 90°。转轴周向与径向幅值相同，且不随测量圆的半径变化；气隙主要是径向分量，由于定子铁心的影响，故周向分量很小；永磁体和定子铁心的周向分量与径向分量不相同，两个区域的周向分量幅值均大于径向分量。

3.2.2 永磁电机外部环境

对于电机外部环境，由于定子铁心的“屏蔽”作用，“泄漏”在环境中的磁场占比十分少，也就是很多文献将其忽略的原因，环境的磁场分布规律如图5所示。仿真与理论结果十分吻合，电机外部环境的周向与径向磁感应强度分量幅值相等，相位相差 90°。不同的测量半径只是影响到磁感应强度幅值大小而已，对相位没有任何影响。

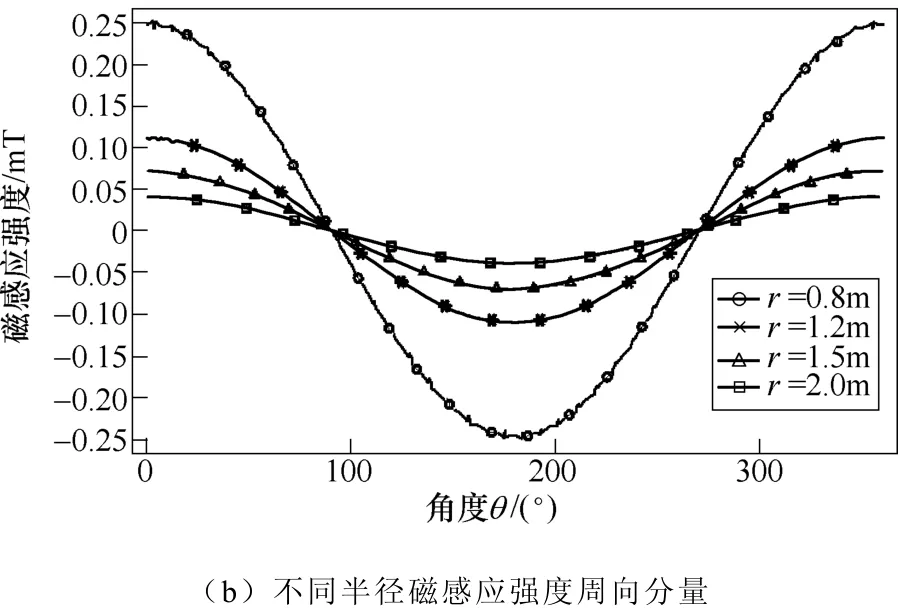
图5 电机外部环境磁场规律Fig.5 Law of external magnetic field of motor

如果只是关心磁场大小，用磁通密度模可以很好衡量，对于圆柱坐标来说，其表示为

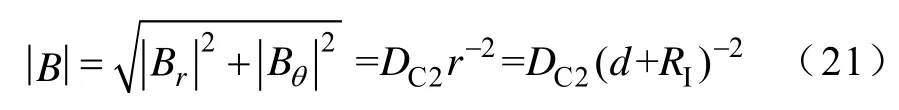
式中，d为距电机表面距离；DC2为磁场系数。

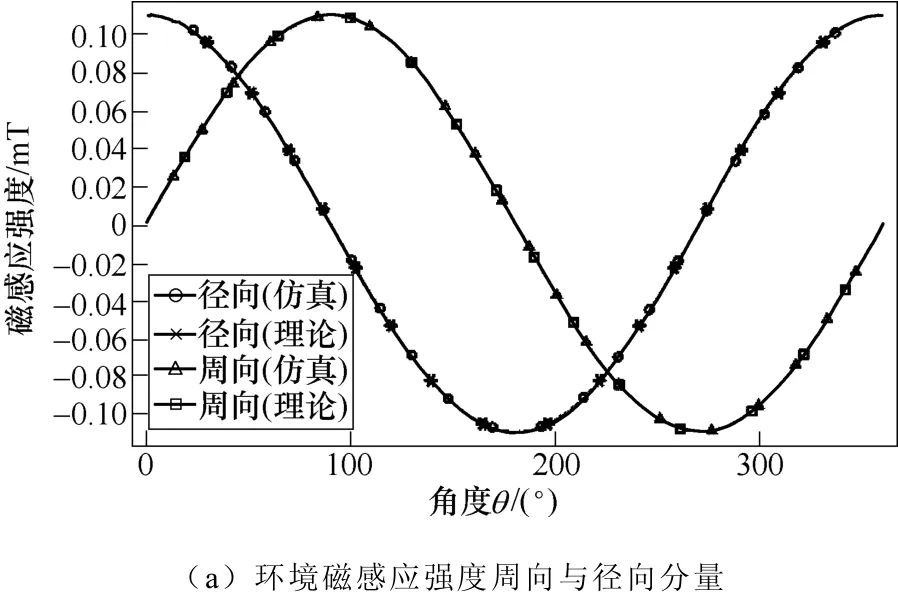
式（21）表示磁通密度模只与d、DC2有关，且与d二次方成反比。理论与仿真结果如图6所示。

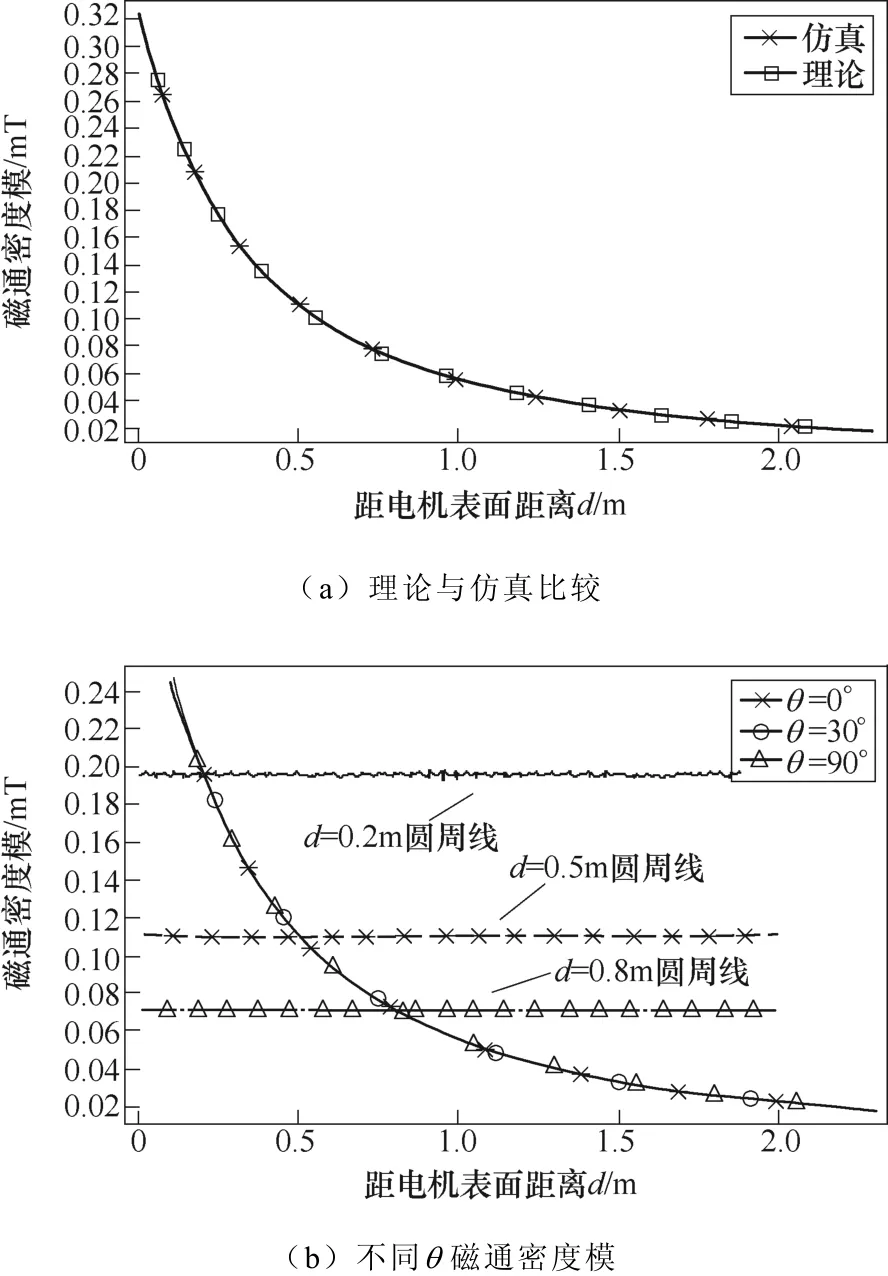
图6 环境磁场衰减规律Fig.6 Low of B in the external environment of the motor

图6a显示了理论与仿真十分吻合，即肯定了模型的正确性；从图6b可知，不同角度θ对磁通密度模没有影响，也即在电机表面等距圆周线上，磁通密度模是相同的，如图中d=0.2m（r=0.9m）、d=0.5m（r=1.2m）、d=0.8m（r=1.5m）圆周线的磁通密度模在圆周线上（与θ无关）均相等，尽管周向分量与径向分量呈现正弦规律（见图5a）。

4 试验分析

磁场测量仪器选用MTB4100B高斯计，精度为±2%，量程为 0～1 000μT；永磁体材料为钕铁硼40H，其剩磁Br为1.25～1.28T，内直径为10mm，外直径为23.5mm，长度为32mm；无齿槽电机定子材料为无取向电工钢WW35−300，内直径为32mm，外直径为55mm，长度为44mm。试验实物如图7所示。

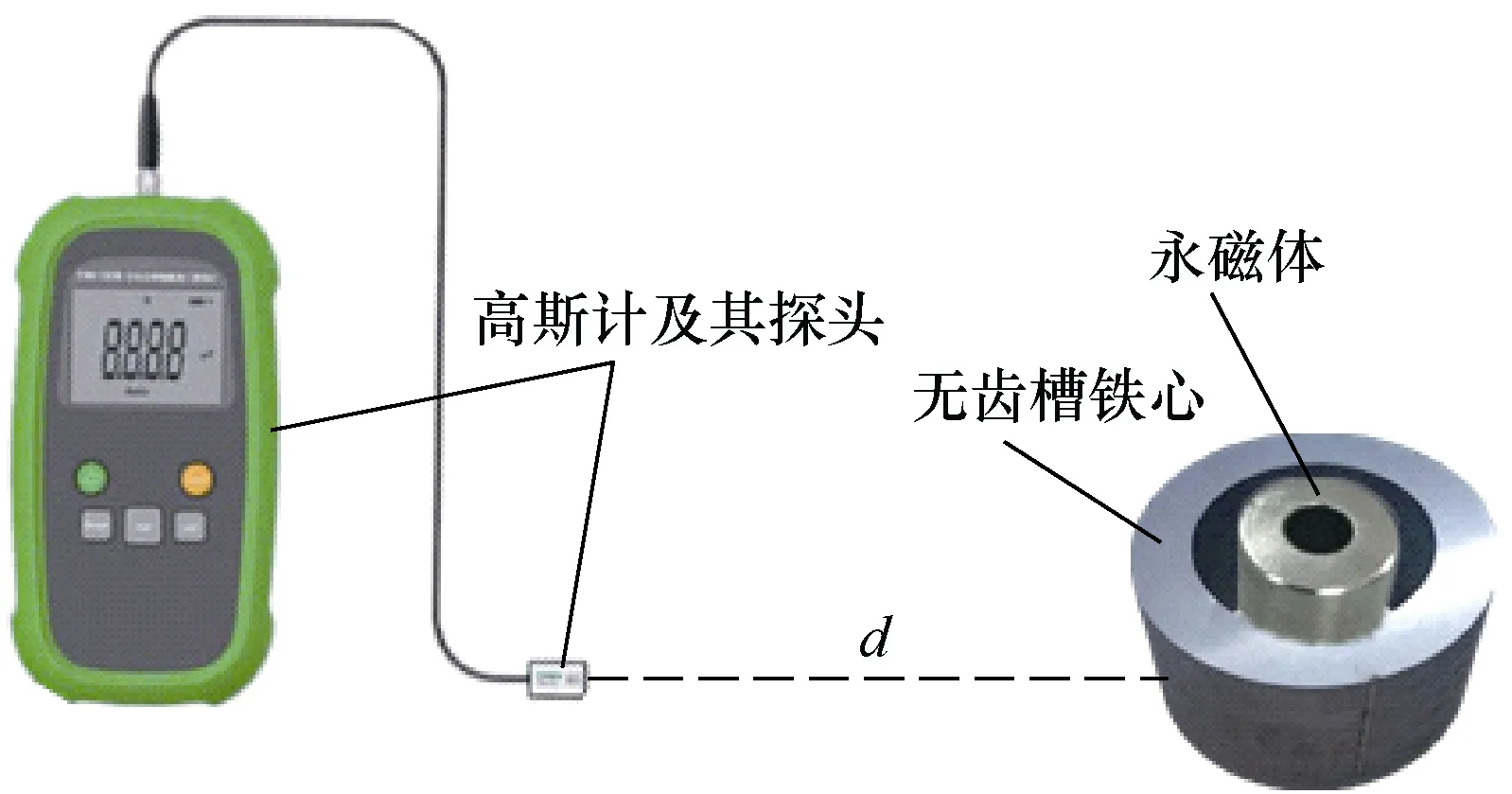
图7 试验实物Fig.7 Experimental prototype

选取一无铁磁性材料、除地磁场外无外加磁场的场地，将高斯计探头置于东西朝向，待仪表显示稳定后按下ZERO键进入相对磁场测量模式，即消除背景磁场的影响。取环境中一测量点r=50mm，d=22.5mm，旋转电机每30°采集一次磁场数据，其径向与周向分量实测与仿真、理论结果对比如图8所示。

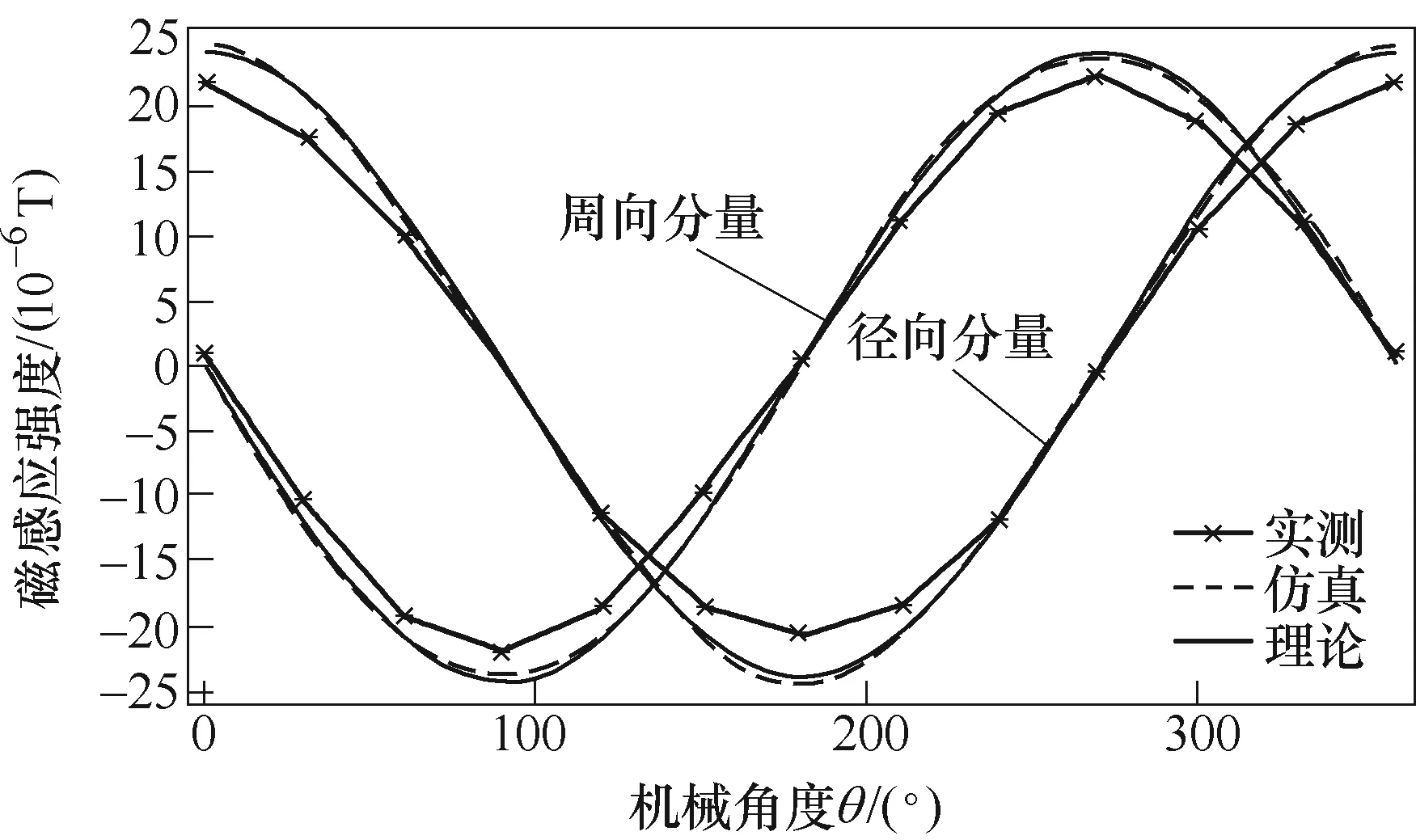
图8 径向与周向对比Fig.8 Comparison result of Br and Bθ

实测结果同样满足正弦规律，与理论值吻合。r=50mm时，其幅值大小与理论结果最大误差约12%。在径向幅值与周向幅值点出选取不同距离进行记录，结果如图9所示。

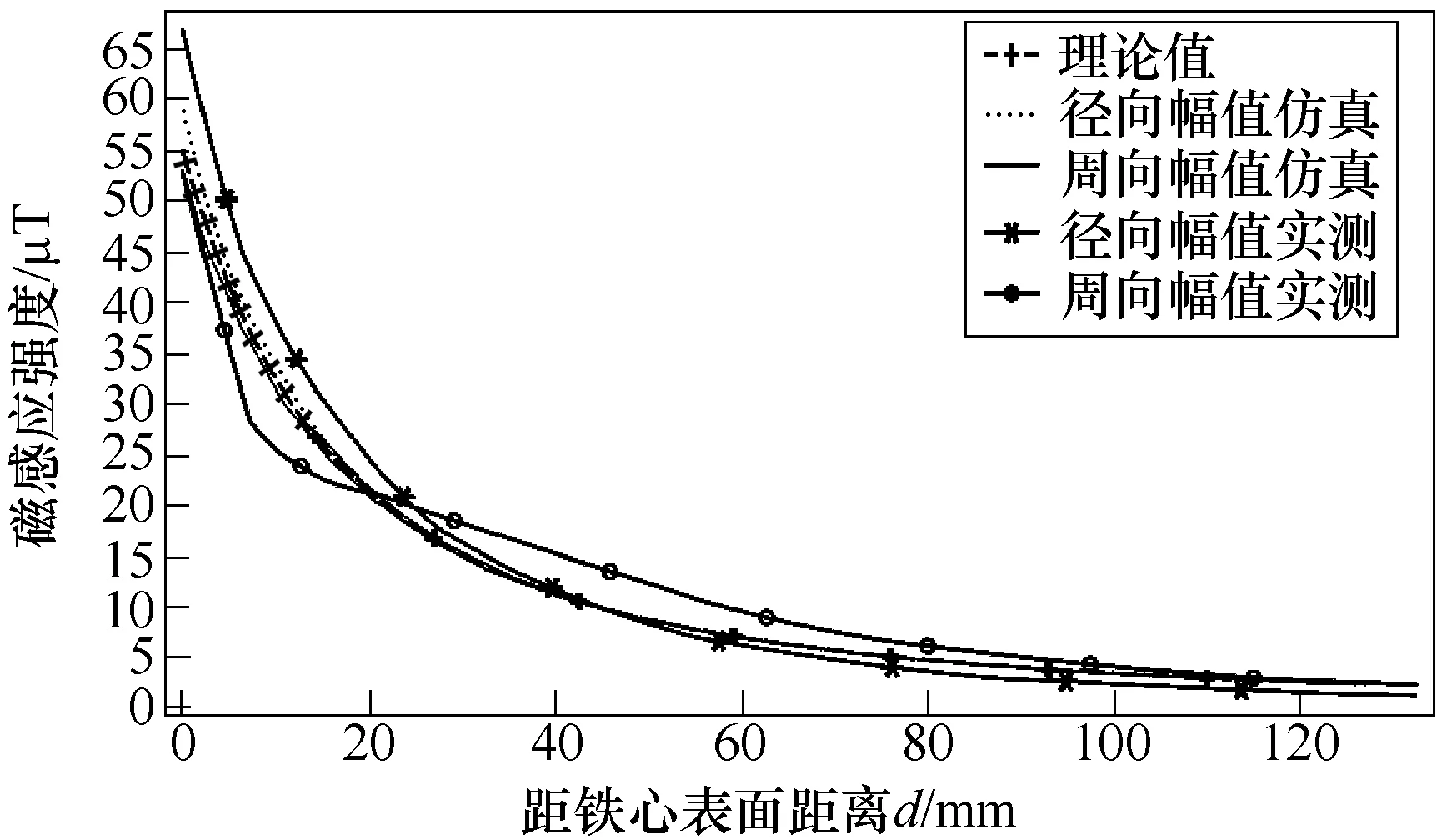
图9 环境磁场衰减规律对比Fig.9 Comparison result of B in the external environment of the motor

衰减规律符合二次方衰减规律，由于铁心饱和影响，径向分量幅值和周向分量幅值衰减规律有一定的误差，理论值虽然没有体现这种小差别，但是也能较好地反映两极电机环境磁场的衰减规律。

5 结论

本文建立了考虑环境漏磁的两极平行充磁电机的理论模型，得出电机内外各个域的磁场精确解析式，各个域的周向与径向磁感应强度均呈正弦分布，周向分量与径向分量相位相差 90°。转轴域的周向与径向分量幅值相同，且不随测量圆的半径而变化；由于定子铁心的影响，气隙域中主要是径向分量，周向分量占比很小；永磁体域和定子铁心域的周向分量与径向分量不相同，两个区域的周向分量幅值均大于径向分量。电机外部环境的周向与径向磁感应强度分量幅值近似相等，在距电机表面地等距圆周线上，磁通密度模是相同的，与距电机表面距离的二次方成反比。

附 录

各个域的磁感应强度系数表达式为