多电机同步运动控制技术综述

叶宇豪 彭 飞 黄允凯

（东南大学电气工程学院 南京 210096）

0 引言

随着工业自动化水平的不断提高，多电机同步协同工作的应用场景越来越多。在纺织与印刷等行业中，为防止过大的张力对材料产生损伤，要求每个环节的多个滚筒同步运转[1-3]。在龙门系统中，两台电机的同步运行能力直接影响着系统的稳定性与精确程度，且由于存在机械上的连接，在同步控制时还需要考虑机械结构带来的影响[4-6]。在XY工作台中，为了能够准确地刻画所需的运动轮廓，需要对两个轴上的电机进行精确的同步控制[7-9]。在工业流水线中，包括等距切割、斜角飞剪、材料填充、纵向切割、拣选和堆放、自动绕线与打包等应用场合，都需要多台电机在变频器与可编程逻辑控制器的配合下实现同步协同工作。

早期的同步控制以机械连接方式为主，包括齿轮啮合、传动杆等方式，物理上的连接较为简单，但存在同步精度低、机械结构易磨损、受限于空间结构与距离等问题，因此需要从电机驱动的角度来突破物理上的缺陷。如今依靠成熟的伺服驱动系统，能够保证电机之间及时地交互转速与位置信息，从而使得同步控制更加容易实现，但是变频器往往只能提供开环的同步控制，存在信息延迟与鲁棒性较低等问题，因此从控制算法上提高同步控制系统性能显得十分重要。

多电机同步控制系统的组成如图1所示，每台电机均有各自的闭环跟随控制，所有电机的实际运行状态通过统一的信息接口反馈到上位机中，上位机一方面给各台电机下发用户指令，另一方面利用得到的反馈信息，通过同步控制结构与算法的配合，输出相应的同步补偿量至每台电机，从而实现消除电机间转速差或保持准确转速比的目的。目前，多电机同步运动控制的研究工作主要集中于同步控制器和跟随控制器上。同步控制器可以采用主令、主从、耦合、虚拟轴等不同控制结构[10-14]，并利用现代控制理论设计合适的控制算法；跟随控制器可以采用滑模、模糊、自抗扰、神经网络、自适应、比例积分微分（Proportional Integral Derivative, PID）等不同控制算法[15-19]，从而加强系统的同步能力。本文以同步控制器为主线，阐述了多电机同步运动控制的主要控制结构和研究进展，仿真对比三种主流控制方案的性能差异，综述了主要研究难点与现有的解决方案，最后给出总结与展望。

图1 多电机同步控制系统的组成Fig.1 The composition of multi-motor synchronous control system

1 主令控制

主令控制是最简单的一种并行控制方式。双电机主令控制结构如图2所示，两套并联的电机控制系统接收同一指令信号，运行状态相互独立。图中，ωref为系统给定的参考转速，ωi、TLi分别为第i号电机（i=1, 2, 3,…,N）的实际转速和负载转矩。

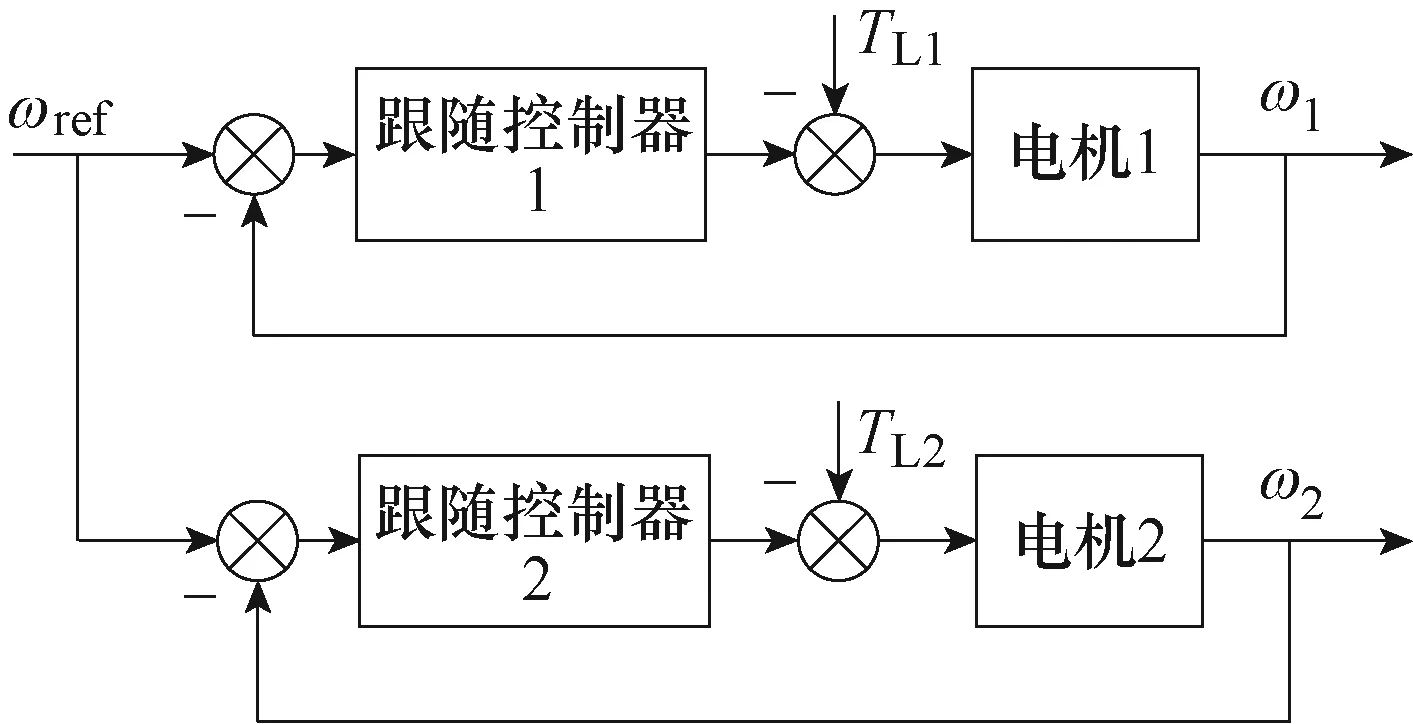
图2 主令控制结构Fig.2 Structure diagram of master control

该方案的优势在于控制结构简单，起停信号无时延，但是由于开环的控制结构使得各支路的运行状态无法交互，同步性能完全依赖于每条支路的跟随能力与抗扰动能力，因而系统整体的同步能力弱。

2 主从控制

在主从同步方式下，将主机的实际运行状态作为从机的参考输入，其控制结构如图3所示。当主机的运行状态发生改变时，从机就会跟着做出相应的改变，但状态的传递是单向的，从机运行状态的变化无法对主机产生影响。同时该方案还存在信号传递时延较大的问题，尤其在起停阶段，一般只用于对同步性能要求较低的场合[20]，也有学者通过滑模、模糊等控制手段对其性能进行优化[21-24]。

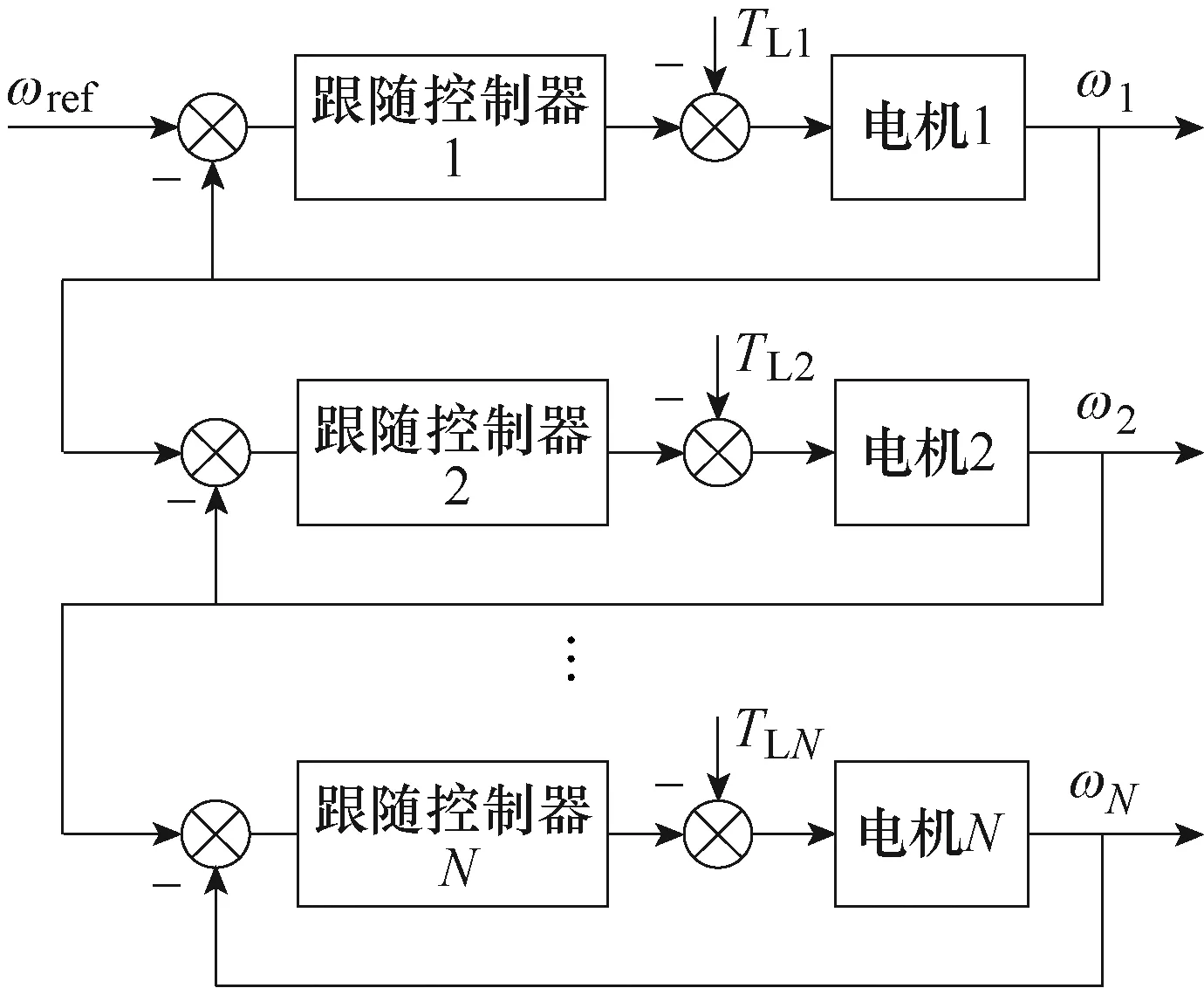
图3 主从控制结构Fig.3 Structure diagram of master-slave control

3 交叉耦合控制

交叉耦合控制是一种闭环的控制方式，最早由Y.Koren[25]于1980年提出，其结构如图4所示，图中，Ki为增益系数。该控制结构在主令控制的基础上，增加了转速误差补偿模块，对电机的转速差进行处理后分别补偿至跟随控制器的输入，实现了电机运行状态之间的耦合。当一方受到扰动而产生转速差时，不仅自身的给定会被补偿以快速对冲这种变化，另一方的给定也会被补偿以跟随对方的变化，从而显著减小了电机之间的转速差，具有较强的抗扰动能力。该方案最适合双电机系统，而面对多电机系统时，结构复杂且补偿效果不够理想。另外，固定增益会带来暂态补偿效果与稳态性能相矛盾的问题。

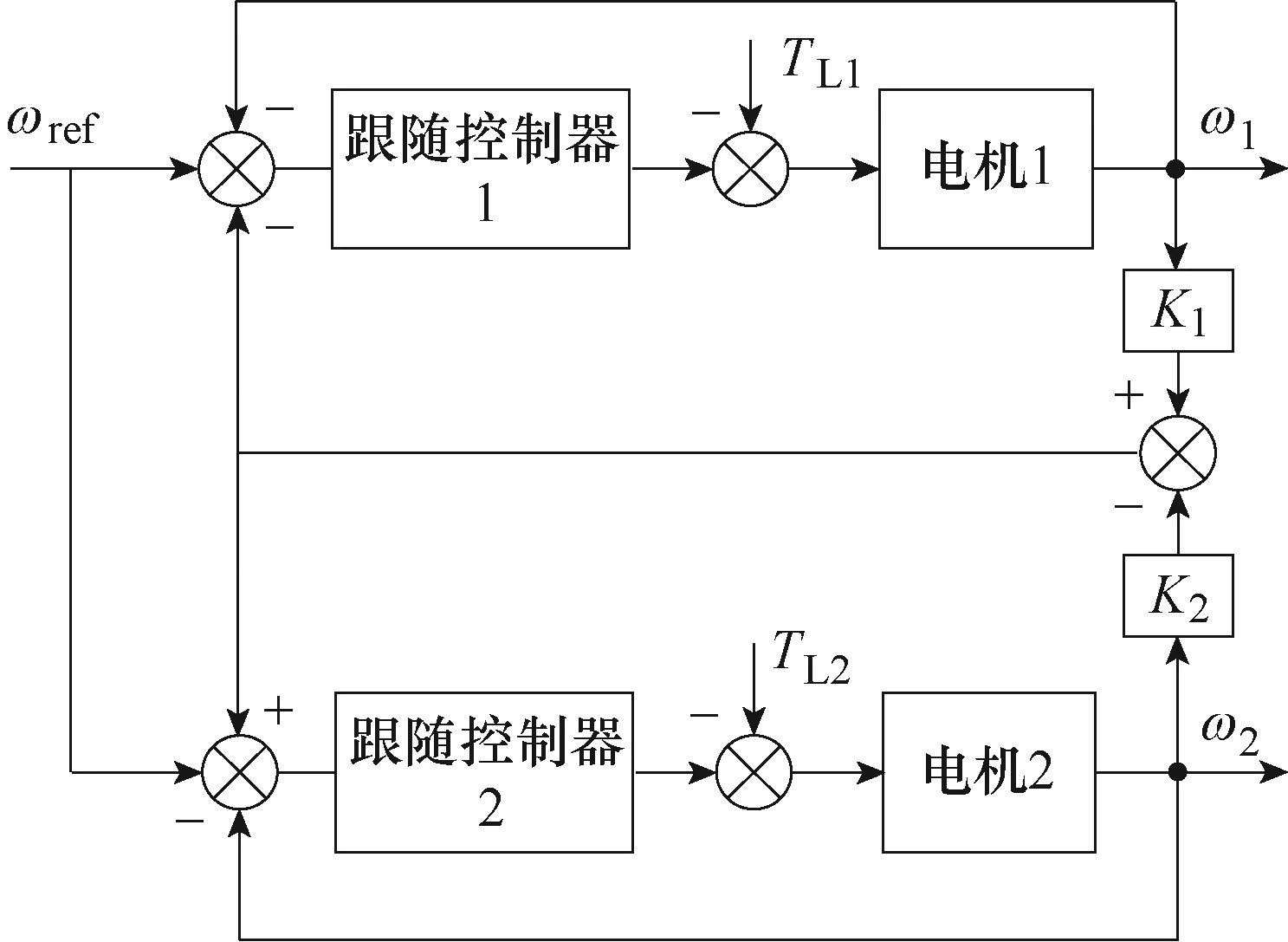
图4 交叉耦合控制结构Fig.4 Structure diagram of cross-coupling control

针对交叉耦合控制存在的固定增益和反馈控制时延问题，Gao Yu等[26]利用转矩观测器，构造了带宽远大于转速环调节器的同步误差调节器，直接对电流环给定信号进行补偿，同时也解决了跟随控制和同步控制相耦合的问题。Xiao Yong等[27]通过设置新的补偿控制表达式，实现了耦合开关的选择控制以及转速比例同步控制，使得控制模式更加灵活。赵希梅等[28]通过将互补滑模跟随控制结合到交叉耦合控制结构中，在精密直驱龙门系统中获得了优异的位置同步效果。齐彪[29]针对双工件台系统，提出了改进型的双交叉耦合控制结构，直接把两个轴向的转角差作为控制目标。夏长亮等[30]利用积分型滑模控制器来提高滑模控制的质量，结合交叉耦合控制有效提升了双永磁同步电机系统的转速同步控制质量。Zhan Lixin等[31]利用自适应模糊滑模控制器来提高滑模控制的质量，结合交叉耦合控制提高了机器人飞机柔性工装系统的工作质量。文献[32]设计了一种基于PID的交叉耦合控制器，其控制效果优于并行的PID控制系统。

在一些存在显著周期性工况的场合，有学者将迭代学习控制引入交叉耦合控制结构，构成了交叉耦合迭代学习控制。文献[8]在XY工作平台上给出了该控制方案的整体收敛性分析，同步误差采用的是双轴各自跟随误差之差，有效收敛了轮廓控制的误差。文献[9]针对交叉耦合迭代控制过程中轮廓误差收敛速度慢、收敛性差的问题，提出一种与经验模态分解算法相结合的改进的两轴间交叉耦合迭代控制方法。

4 相邻耦合控制

相邻耦合控制是针对多电机同步控制场合的一种耦合控制方式，最早由Sun Dong等[33]于2002年提出，其结构如图5所示。图中，ε ij为电机i与电机j之间的同步误差（i,j=1, 2, 3,…,N）。

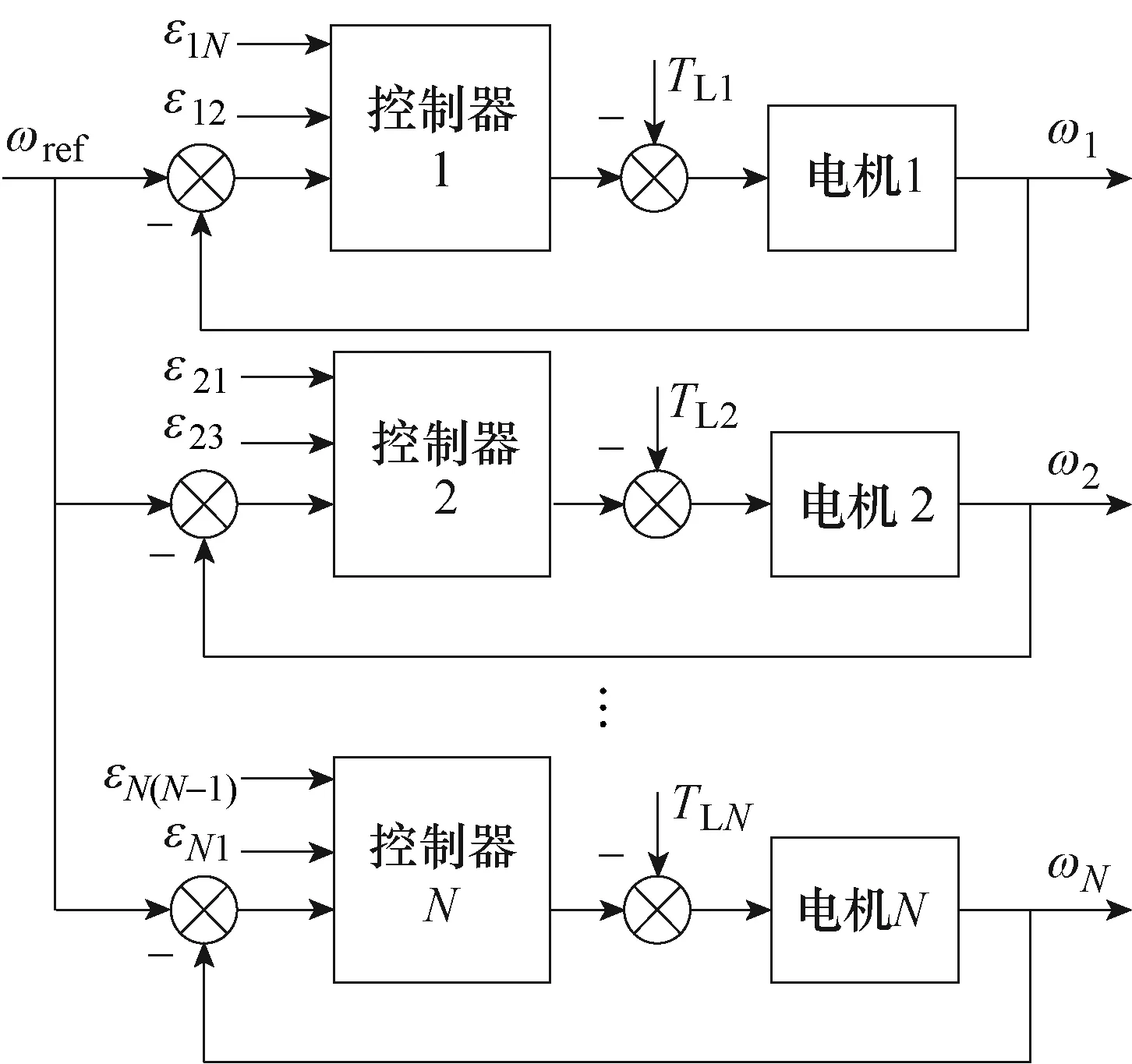
图5 相邻耦合控制结构Fig.5 Structure diagram of adjacent coupling control

该控制结构利用了最小相关个数的思想，在单个电机的转速补偿中考虑相邻两个电机的运行状态反馈，因而单个电机的控制器由一个仅与自身相关的跟随误差控制器和两个受相邻电机影响的同步误差控制器所组成，其结构如图6所示。图中，eN为第N台电机的跟随误差。

图6 相邻耦合控制中控制器的结构Fig.6 Structure diagram of controller in adjacent coupling control

该方法克服了交叉耦合结构只适用于双电机的缺陷，在最小相关的思想下控制结构易于实现，当电机数量较多时，控制器的算法不会变得复杂。但不足在于，某个电机产生的误差只能向两侧顺次传递，无法实时传递给其他所有电机。同时控制器的数量3倍于电机数量，运算量较大。

大连理工大学的孙建忠等[34-35]于2009年提出了环形耦合控制结构，如图7所示。该控制方案中，对电机转速给定的补偿仅与相邻的一台电机相关，信号的传递是环形的单向传递。该方案减少了补偿器数量，在保证同步性能的基础上降低了运算量。缺点在于当电机数量增加时，误差传递迟滞问题会更加严重。

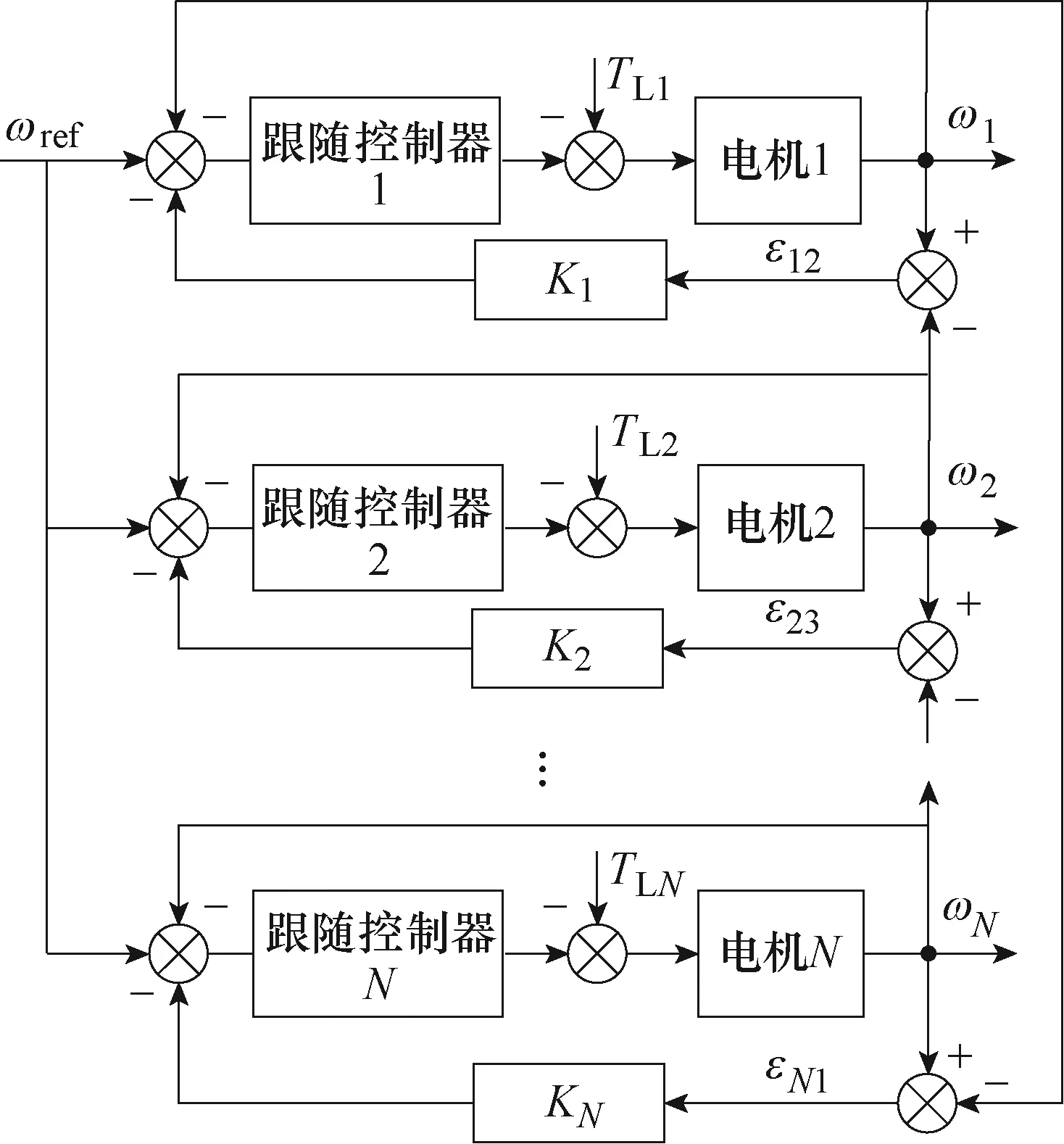
图7 环形耦合控制结构Fig.7 Structure diagram of ring coupling control

此外，Chen Qiang等[36]通过定义新的同步控制器输入信号构成，加以自抗扰控制和积分型滑模控制来提高相邻耦合的性能。张承慧等[37]提出一种基于最小相关轴数目的同步控制思想，并在此基础上设计了基于相邻耦合误差的同步控制算法。文献[38]针对非线性振荡系统中的多台感应电机激振器，利用相邻耦合控制结构和自适应全局滑模算法，实现了对速度和相位的同步控制。文献[39]设计了新的相邻耦合误差表达式，并通过滑模控制的手段实现了较好的性能。文献[40]将相邻耦合控制策略应用于直线开关磁阻电机位置同步控制中，有效实现了3台电机的同步。

5 偏差耦合控制

F.J.Perez-Pinal等[41]提出的偏差耦合控制是对交叉耦合控制在多电机场景下的优化，补偿信号由系统中所有电机的运行状态共同决定，其控制结构如图8所示。将被控电机的实际速度与其他各个电机的实际速度分别作差后乘以一适当系数Kij，求和后作为被控电机的控制输入补偿，该系数通常取为各电机转动惯量J的比值，即Kij=Ji/Jj。其结构如图9所示。

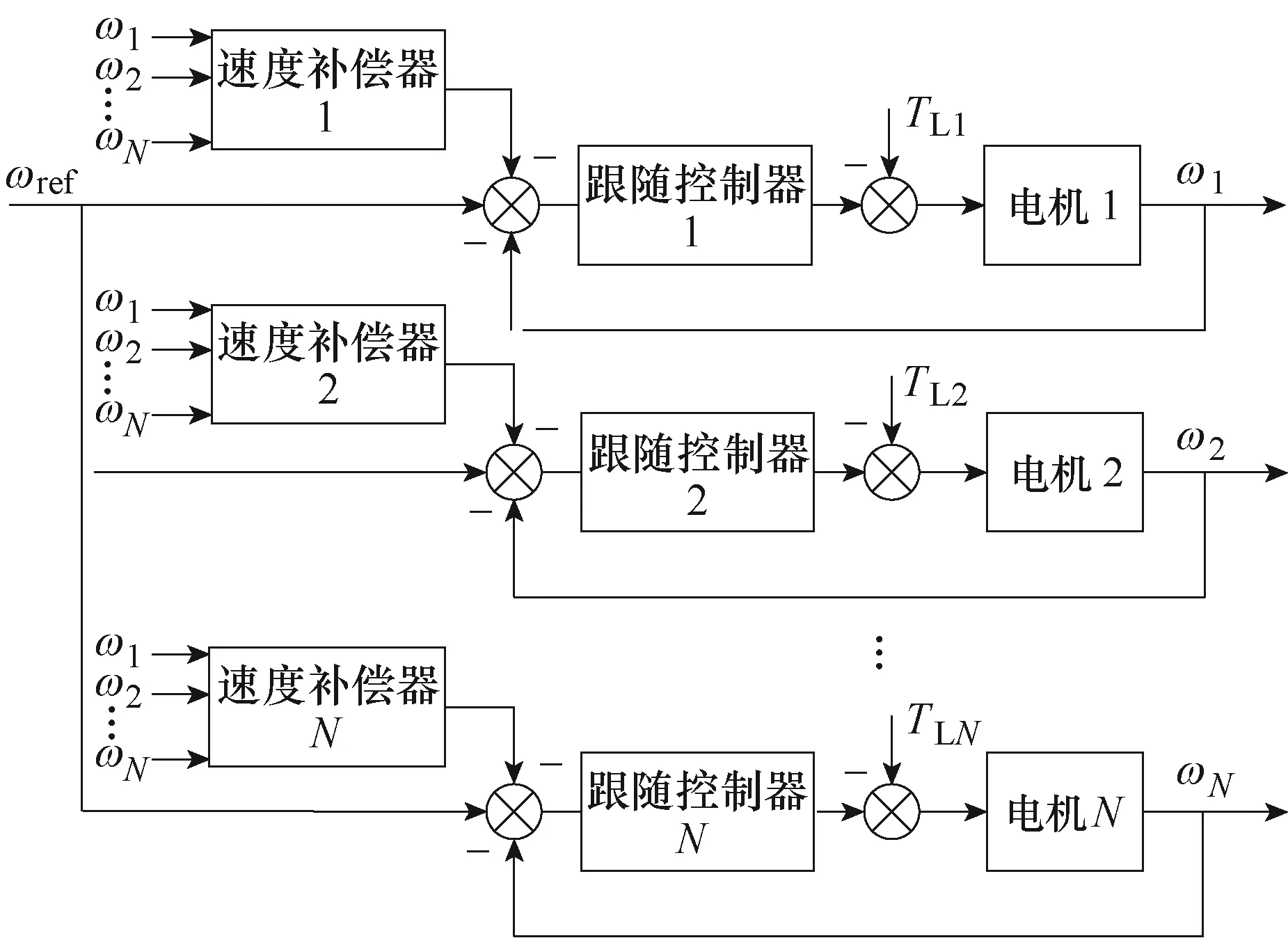
图8 偏差耦合控制结构Fig.8 Structure diagram of relative coupling control

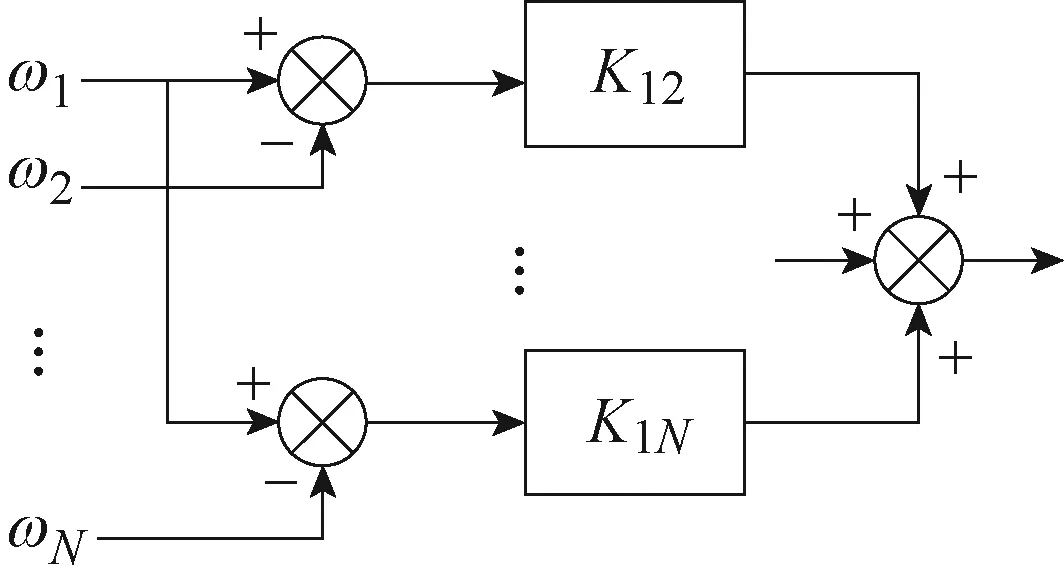
图9 第一台电机速度补偿器结构Fig.9 Structure of speed compensator of the first motor

该控制结构的优点在于系统的耦合程度高，任一电机出现的转速波动信息都会传递给其他电机以采取相应的补偿动作，控制时延低，具有较好的同步能力。其不足之处在于，每个补偿器都要考虑所有电机的转速信息，当系统中电机数量增多时，不仅补偿器的数量会随之增加，单个补偿器的复杂程度也在增加，从而整体的运算量极大增加。

最初的偏差耦合结构使用的是基于电机转动惯量的固定增益补偿，只考虑了电机的转动惯量对同步性能的影响，当负载变化大时，系统波动较大，甚至会导致系统不稳定，针对此问题，彭晓燕等[42]提出一种考虑多因素的改进型PI同步速度补偿器，结合自适应模糊滑模跟随控制器提高精度。谢炜[43]改进了补偿结构，提出了一个速度指标量，这个指标量与多电机同步控制系统中每台电机的转速有直接的相关性，从而增强了系统的耦合程度。程文雅等[44]将跟踪误差评价和耦合误差的概念引入补偿机构，提高了补偿机构的执行效率，结合反步模糊滑模的跟随控制方法获得了优秀的同步性能。张谦[45]借用三环控制的思想设计了更为有效的同步补偿机制，引入了转矩偏置补偿的概念，以更好地处理转矩负载扰动问题。王国亮[46]采用遗传算法整定模糊PID同步补偿器，将模糊控制运用于PID参数调节，动态调节参数以获得最佳的性能。沈阳工业大学崔皆凡等[47-48]将神经元PID与神经网络PID等控制方法运用于同步控制，并利用模糊控制等方式对偏差耦合结构提出了诸多改进之处。天津工业大学耿强等[49-50]对偏差耦合控制同步补偿器提出了新的数据比较方式与补偿算法，并提出最大速度同步误差和最大加速度概念。哈尔滨工业大学伞冶等[51-52]针对大功率随动系统的多电机同步控制，基于偏差耦合同步控制方式，与相邻耦合控制相融合，提出了相平面分区控制方法，提高了同步补偿精度。

6 虚拟主轴控制

虚拟主轴控制结构最早由K.Payette[53]在R.D.Lorenz和P.B.Schmidt[54]的工作成果上发展而来，其结构如图10所示。

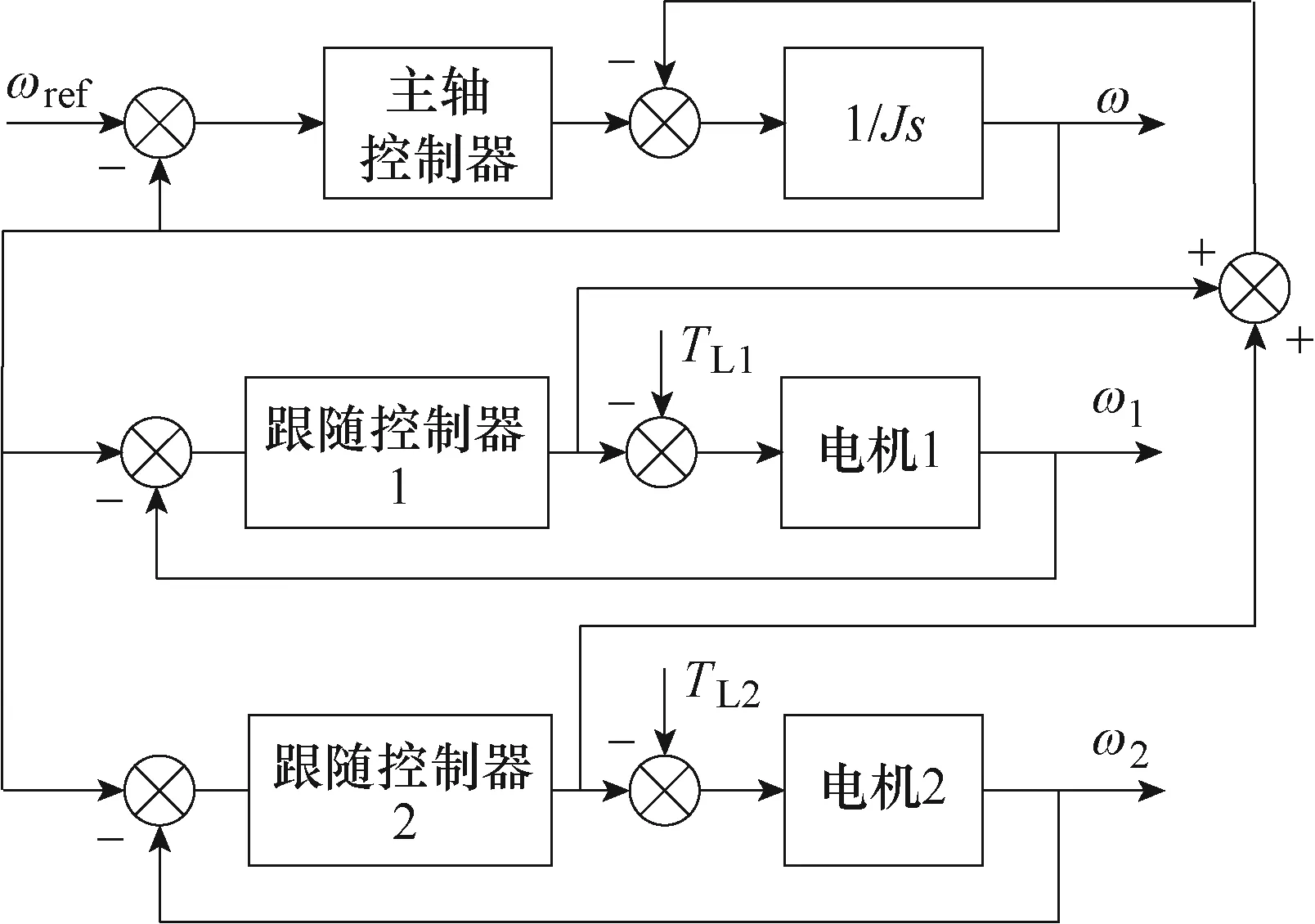
图10 虚拟主轴控制结构Fig.10 Structure diagram of virtual spindle control

该控制方式模拟机械主轴的拖动特点以实现多电机的同步控制，将多电机的实际运行转矩反馈到虚拟的主轴上，主轴对反馈的转矩进行输出调整，从而带动从机恢复到同步的状态。该方法成功地用电信号复制了机械主轴的特性，但也存在着给定信号时延和虚拟主轴惯量难以确定等问题[55-56]。

华中科技大学的张李超团队[57-58]对双螺杆伺服压力平台采用了虚拟主轴的控制方式，利用主从机转速和转矩解耦的方式，获得了理想的控制性能。浙江大学方攸同团队[59-60]对高速列车的多电机同步牵引方案展开深入的研究，实现了用于4台600kW永磁同步电机的虚拟主轴同步控制系统。

7 仿真对比

为对比上述几种同步控制方法的性能和适用场合，本文选用400W伺服电机，对常用的交叉耦合控制、相邻耦合控制和偏差耦合控制进行对比研究。首先，定义了反映跟随性能与同步性能的参数指标。然后在 Matlab/Simulink仿真环境下对上述几种同步控制方法的起动过程、暂态过程和稳态阶段进仿真对比。其中，第一组对比为双电机情况下的交叉耦合与偏差耦合，第二组对比为4台电机情况下的相邻耦合与偏差耦合。

定义跟随误差为

式中，i为电机编号；k为采样时刻；为给定转速；为实际转速。定义同步误差为

采用相邻两电机之间环形相减的方式得到。

令E和D分别为跟随与同步的误差指标，下标m、p分别代表误差的绝对值均值的方均根和峰峰值的方均根，则Em、Ep、Dm、Dp分别为

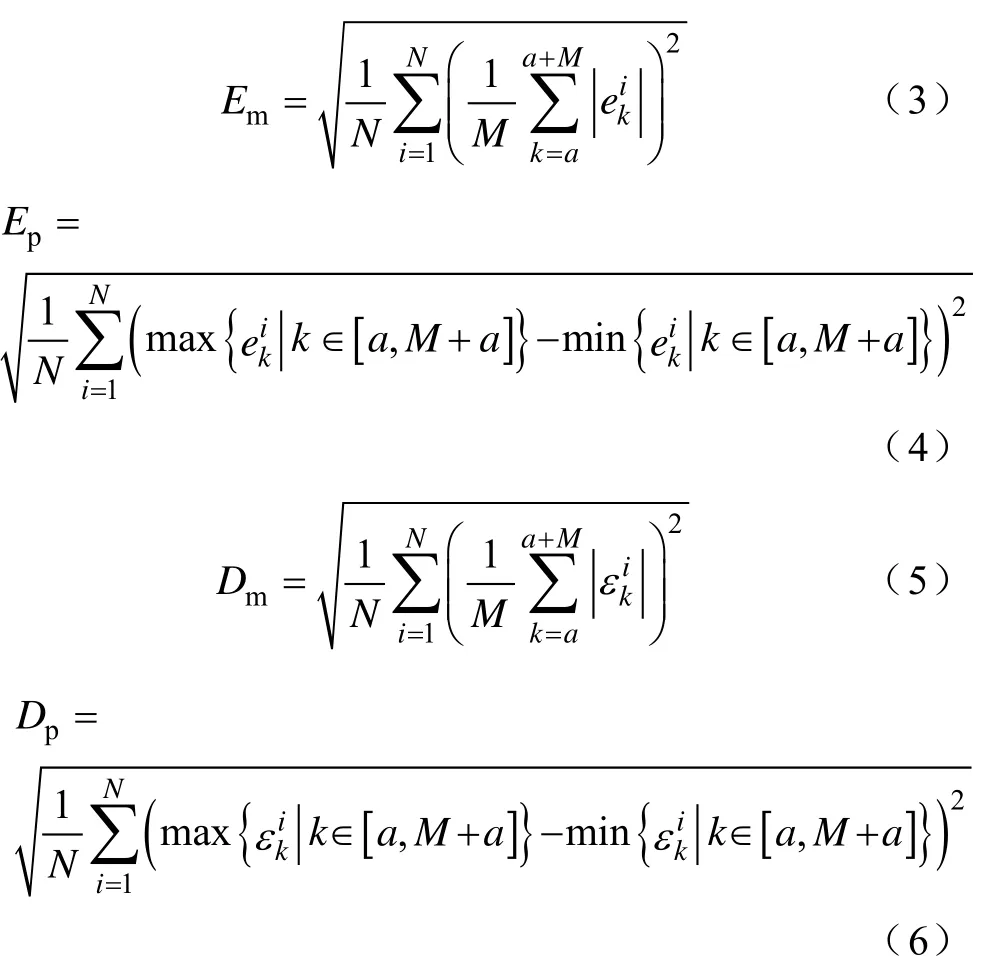
式中，a、M、N分别为不同状态下的开始采样点、状态区间长度、系统内电机的数量。

除转动惯量外，4台电机的电磁参数均一致，每相电阻Rs=2.2Ω，d、q轴电感Ld=Lq=5.93mH，极对数p=4，每相磁链幅值fψ=0.061 2Wb，额定转速3 000r/min，额定转矩TN=1.3N·m。为模拟不同的工况，4 台电机的转动惯量分别为：J1=2.9×10−5kg·m2,J2=2.5×10−5kg·m2,J3=2.3×10−5kg·m2,J4=2.1×10−5kg·m2。4台电机的负载转矩分别在 0.15s, 0.1s, 0.125s,0.175s处由 1.3N·m 变为 0.65N·m。

第一组对比的仿真波形如图11和图12所示。

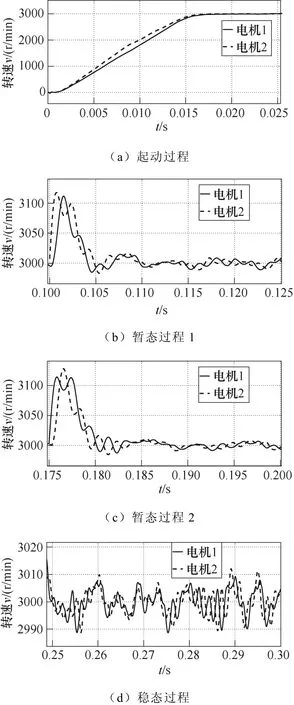
图11 交叉耦合双电机运行情况Fig.11 Cross-coupling dual motor operation

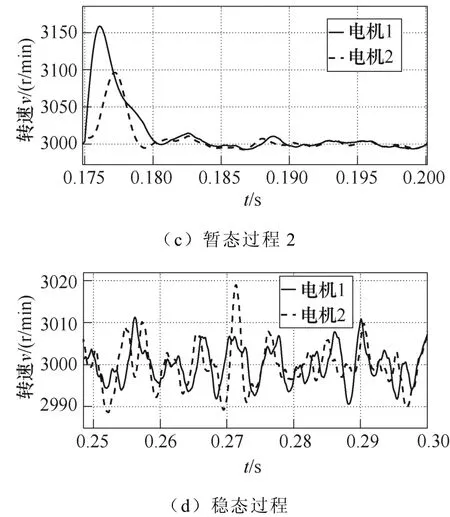
图12 偏差耦合双电机运行情况Fig.12 Relative coupling dual motor operation

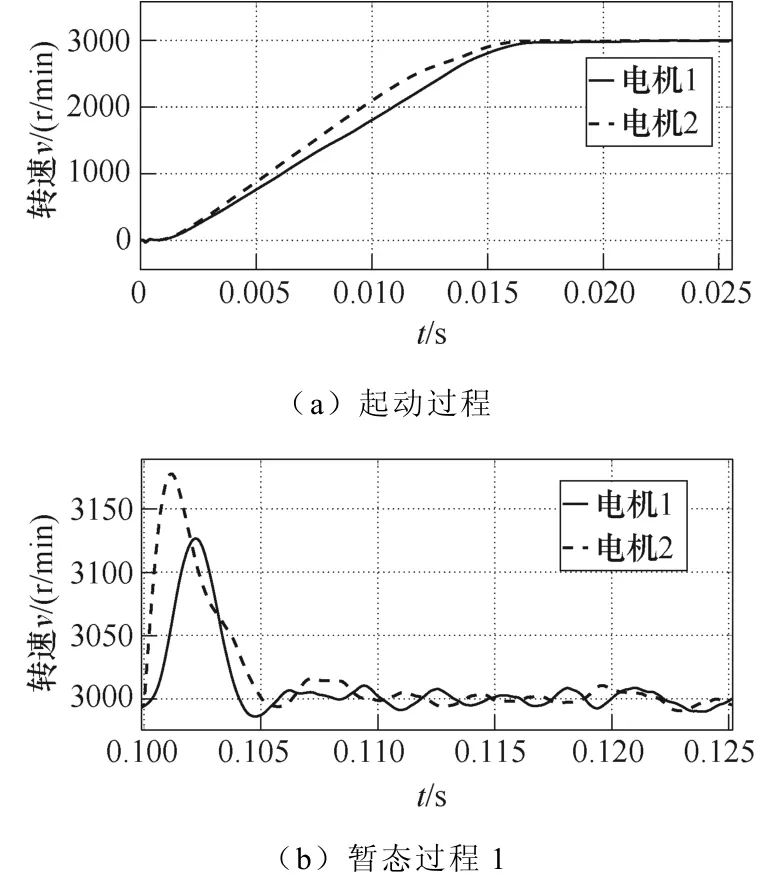
根据仿真结果对比各组数据，交叉耦合与偏差耦合的跟随与同步误差指标对比如图13所示，所有结果均根据给定转速做百分化处理。

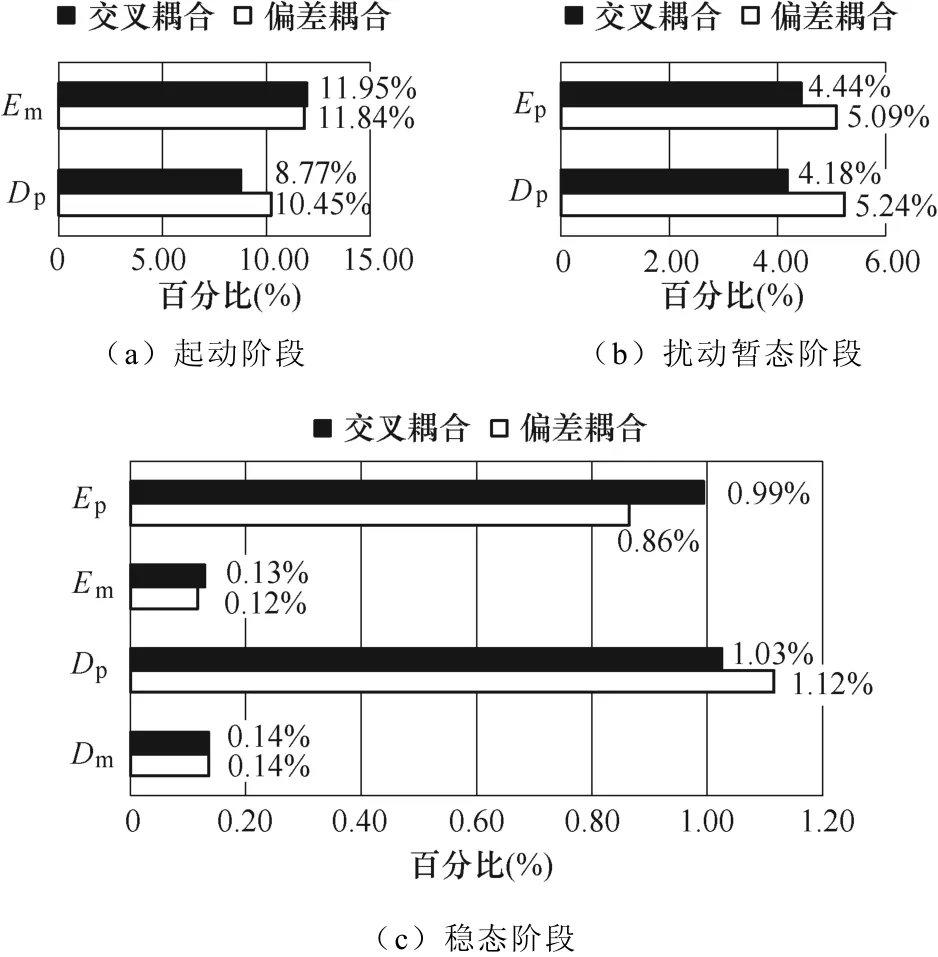
图13 交叉耦合与偏差耦合的跟随与同步误差指标对比Fig.13 Comparison of tracking and synchronization error indexes between cross-coupling and relative coupling

根据指标对比的结果可知，交叉耦合控制在起动和负载扰动情况下有更小的跟随与同步误差，而偏差耦合控制的优势主要体现在稳态性能上。另外，虽然给出了双电机情况下的对比，但是偏差耦合控制更容易拓展至多电机同步控制。

第二组对比，即四电机情况下的相邻耦合与偏差耦合的仿真波形分别如图14和图15所示，根据仿真结果计算并对比各组数据，相邻耦合与偏差耦合的跟随与同步误差指标对比如图16所示。

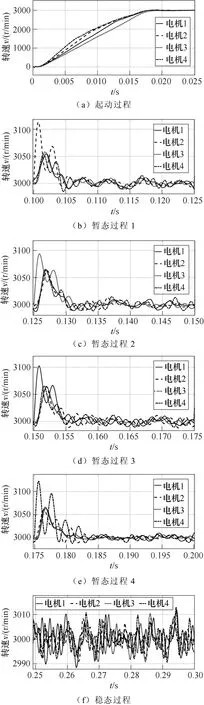
图14 相邻耦合四电机运行情况Fig.14 Adjacent coupling quadruple motor operation

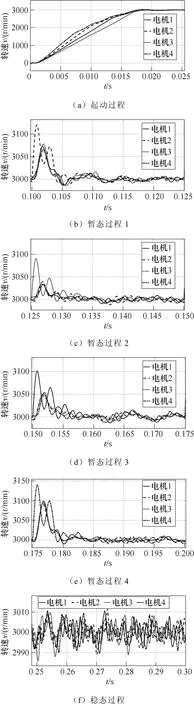
图15 偏差耦合四电机运行情况Fig.15 Relative coupling quadruple motor operation

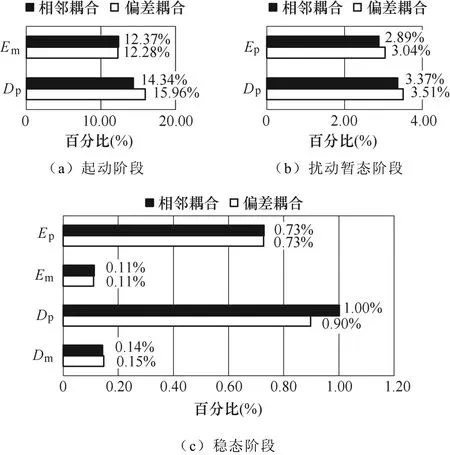
图16 相邻耦合与偏差耦合的跟随与同步误差指标对比Fig.16 Comparison of tracking and synchronization error indexes between adjacent coupling and relative coupling

根据指标对比的结果可知，相邻耦合控制与偏差耦合控制具有相近的跟随能力与同步能力。虽然相邻耦合控制的控制器少、结构简单，且综合误差略小，但是由于其误差传递的结构导致系统对扰动的响应速度较慢，因此这两种控制结构需要根据被控系统的实际需求进行选择。

8 主要研究难点

8.1 电机数量与控制层面

一方面是由双电机的同步控制向多电机同步控制甚至多电机集群同步控制的延伸发展。文献[61]针对机械臂中的多电机协同控制需求，在结合了主令、主从、交叉耦合三种控制结构的特点后，提出了基于模糊控制的新型环形耦合控制方法，有效地提高了同步能力。文献[62]在多电机集群控制环境下，根据盾构机的实际工况设计了新的区域耦合控制拓扑，在降低系统复杂程度的同时保证了同步精度。文献[63]为了简化在多电机同步情况下的补偿器数量和系统运算量，提出了平均值偏差耦合控制方式。文献[64]针对负载惯量变化给多电机驱动平台带来的影响，将多电机同步结构置于平台位置控制闭环内，结合惯量辨识的方法，取得了有效的同步。

另一方面是从针对单个电机的调节上升到对系统整体层面的调节控制。传统耦合方法不考虑每个电机转速在系统中的权重，且一系列改良算法大多只考虑了提高每个电机的运行性能，而不从改善系统整体架构性能的角度出发，文献[65]提供一种从整体看问题的方法，添加了额外的参考速度控制器以获得更好的整体性能。文献[66]利用协同控制算法区分不同电机在系统中的重要程度，从而提高了系统整体的鲁棒性和协调性，且易于拓展至超过三电机的多电机同步系统。文献[67]针对多层次多轴系统，利用主从结构与环形耦合结构的结合，提出了一种基于组合交叉耦合误差的控制方法，取得了理想的同步性能与抗扰动能力。文献[68]在多机械手电机网络化系统中，设计了双层次控制结构，第一层对于单机械手上的多关节电机，采用模糊 PID作为跟随与同步控制器，第二层针对多个机械手，设计了预测控制机制，从而保证了系统整体的性能。

8.2 位置同步与速度同步的关系

早期的同步控制研究以速度同步控制为主，但越来越多的伺服应用场景对位置同步提出了要求。文献[69]专门针对位置同步控制，提出了改进型的交叉耦合结构，对补偿器的输入输出以及算法逻辑进行了调整。文献[70]对普通交叉耦合结构进行了自适应控制改造，实现了多电机的位置准确同步。文献[71]则是在交叉耦合结构的基础上，通过分别设计位置与转速同步补偿器，同时实现了转速同步与位置同步控制。文献[72]针对双直线电机位置伺服系统中的时变轨迹问题，提出了利用Sugeno型模糊神经网络的同步控制器，结合互补滑模跟随控制器的方法，在对比实验中显著提高了同步精度。文献[73]设计了能够同时估计集总扰动和系统状态的广义扩张状态观测器，结合同步解耦控制器，实现了对网络化多轴运动系统的高精度位置同步控制。

8.3 模型不确定性与参数敏感性

跟随控制器的设计往往需要考虑被控对象的实际模型，而工业中往往无法对对象进行精确的建模。文献[74]设计了基于预测的自适应鲁棒控制策略，使得在存在未知非线性情况下，依旧实现了多电机伺服驱动系统的同步控制。文献[75]在偏差耦合控制结构的基础上，将模糊控制作为转速补偿控制方案，在系统内电机的转动惯量存在显著差别的情况下依旧保持了高精度的同步。文献[76]通过引入具有直流电机标称参数值的扰动动态模型，显式地处理了参数和负载变化问题，使用自调节同步补偿器和基于扰动观测与比例控制的跟随控制器，实现了优异的控制效果。文献[77]通过自适应鲁棒控制器，提升了同步补偿器的调节能力与性能，降低了系统对模型和参数的敏感性。

8.4 跟随控制算法运算量

由于高级智能算法的运算量较大，常常不适用于低级的处理器，且无法满足特定场合的需求。文献[27]结合交叉耦合结构设计了最优 PID算法，实现在降低运算量的情况下保证控制精度。文献[78]使用主从控制与交叉耦合控制结合，以虚拟轴的形式作为主机给定信号，利用模糊PID设计同步控制机构，并省略跟随控制器，在液电双轴、双电机轴等工况下取得成功。文献[79]利用非线性 PID，在保留普通PID计算优势的基础上，提高了控制的收敛速度与稳态性能，并一定程度上提高了鲁棒性。

8.5 跟随控制与同步控制的解耦

常用的同步控制方案将跟随控制与同步控制混合在一起，导致性能相互牵制，控制主体不清晰不明确，为此不同学者在解耦控制方面做出了努力。文献[26]通过增大同步控制器的带宽以强调同步控制的优先作用。文献[80]根据最优控制原理，分别设计了跟随控制器和同步控制器，基于平均值偏差耦合控制策略，提出了同步控制内环、跟随控制外环的解耦控制结构。文献[81]研究专用于高精度龙门运动平台的同步控制方法，控制模型使用单纯的解耦控制的方法，利用两个控制器，分别进行跟随控制和同步控制。

8.6 齿隙非线性问题

针对有齿轮啮合于各电机之间的多电机同步系统，需要充分考虑齿隙非线性对控制系统精确程度带来的影响。文献[82]针对未建模的动态过程和具有齿隙非线性的双电机伺服系统，提出了基于改进型扩张状态观测器的快速递归动态滑模控制，通过在扩张状态观测器中引入新的非线性函数，简化了控制器的设计流程，提高了系统的跟踪准确性。文献[83]进一步利用递归自适应积分滑模控制解决到达相位和奇异性问题，处理了齿隙非线性带来的影响。文献[84]使用了模糊滑模自适应控制的方式来解决该问题。

9 结论

多电机同步控制技术是保证复杂机电系统中各个执行部件协同工作的关键技术。本文综述了多电机同步控制技术的主要结构、设计思想、相关应用及其优缺点和改进方案，通过仿真对比了几种主要同步控制方法的特点。综合而言，主令控制与主从控制作为初级的开环控制方式，在一些精度要求较低的场合依然有着广泛的应用；交叉耦合控制作为双电机同步系统中常用的控制结构，已经得到了十分完善的发展，同步精度也可以控制在较高的水平；相邻耦合与偏差耦合控制继承了交叉耦合的思想，广泛运用于多电机同步控制的应用中，两者具有相近的同步能力，但是相邻耦合存在误差传递时延问题，偏差耦合存在运算量过大的问题；虚拟主轴控制模拟了机械主轴的同步能力，通常适用于单个电机达到输出极限的应用场景。在实际的应用中，需要综合考虑同步精度、跟随精度、计算量、成本等因素来选取合适的控制方案。

结合多电机同步控制技术的研究难点与主要研究成果，总结了未来的发展趋势：

1）更高的控制精度。通过更加优化的控制结构与算法来进一步提高跟踪精度与同步精度。

2）更高的可靠性。通过应对模型不确定性与参数敏感性，提高极端工况下容错能力等方式，确保系统稳定运行的能力。

3）更大的控制规模。针对大规模电机集群与大空间跨度协作系统，结合适当的控制结构与实时通信手段以实现有效控制。

4）更高的专用性。根据系统的实际运行工况的需求和特性，开发具有针对性的控制方案。