QT800-2 球墨铸铁表面激光熔覆工艺参数多目标优化

张胜江，王明娣，倪超，徐悠源，尹梓航，林瑶，郭敏超，王贤宝

（苏州大学 机电工程学院，江苏 苏州 215000）

激光熔覆能形成强度、耐磨性等综合性质较好的熔覆层，是一项拥有广泛应用前景的表面处理技术。但目前在应用激光熔覆时也存在一些问题，如熔覆层塌陷、裂纹、孔隙等[1-2]。研究表明，这些问题可以通过工艺参数优化[3-5]来解决。传统的优化算法都具有一定的局限性，而基于神经网络利用算法（遗传算法[6-8]、粒子群算法[9-11]等）来优化，具有可行性和通用性。其中NSGA-II 遗传算法能进行全局优化，较为灵活，从而实现多目标寻优，有效提高激光熔覆的熔覆层质量，提升经济效益。

目前国内外学者已对激光熔覆工艺参数的优化算法进行了很多研究。方琳等人[12]利用Kriging 方法建立P20H 钢上熔覆层各质量目标与工艺参数的数学模型，并采用NSGA-II 遗传算法寻求出满足设计要求的最优参数。Kriging 能够给出最优线性无偏估计，但在处理非线性问题时具有一定的局限性。倪立斌等人[13]利用BP 神经网络建立了熔覆带宽度、高度与熔覆工艺参数之间的预测模型，并结合粒子群算法对熔覆过程中的工艺参数进行寻优，最终验证优化结果。PSO 算法收敛速度快，但收敛结果易受参数大小和初始种群的影响。Marzban 等人[14]设计L9 正交试验研究工艺参数对熔覆高度、宽度和深度的影响，随后进行主成分分析以确定每个参数的权重影响，以此采用TOPSIS 算法进行过程参数的寻优，并通过验证试验对最优解检验。TOPSIS 算法能逐渐贴近各目标最优理想解，但其只反映各目标内部的相对接近度，不能反映与整体最优方案的相对接近度。

前人的研究已经证实优化算法对参数的优化卓有成效。在QT800-2 球墨铸铁基体材料表面激光熔覆铁基合金粉末，其熔覆层质量有多个指标，NSGA-II算法能够快速寻找这些指标的最优结果。本文以激光功率、送粉率、扫描速度为优化参数，熔覆层表面粗糙度和硬度为优化指标，通过极差分析得到正交优化结果；然后通过MATLAB 神经网络工具箱建立预测模型，改进NSGA-II 算法得出最终优化结果，与正交试验结果进行比较；最后分析了优化后的工艺参数对基材性能的影响。

1 试验

1.1 材料和设备

本试验熔覆粉末选用铁基339 粉末，该粉末成本低，耐磨性能较好，适用于要求局部耐磨性高且容易变形的零件熔覆，其成分以及主要性能如表1 所示。

表1 熔覆层粉末材料性质Tab.1 Material properties of cladding layer powder

基材选取直径为23.5～26.5 mm 的QT800-2 球墨铸铁，具有较高的强度、耐磨性，广泛应用于铸造行业。基材性能如表2 所示。

表2 基体材料性质Tab.2 Properties of the base material

本文选用的激光器为YLS-6000-CT-Y11 型光纤激光器，激光功率由光纤激光器连续调节，输出功率达6000 W。该激光器内置一路输出光光耦合器，采用水冷的冷却方式。送粉设备为RC-PGF-D2 双桶式同步送粉器，送粉连续稳定，可精确控制送粉量和载粉气流。旁轴送粉的粉末输送装置在激光束一侧，在高能量密度的激光束照射下，涂层粉末先与激光束接触，再和基体表面薄层快速熔化并急冷，形成熔覆层，粉末利用率较高、通用性较好。

1.2 方法及结果测量

激光熔覆过程涉及很多参数，根据先前的文献和经验[15-20]，本试验选择激光功率、扫描速度、送粉速度作为优化的工艺参数。选择表面粗糙度和表面硬度作为评价熔覆层质量的指标。送粉气流量为8 L/min，气压为0.5 MPa，三爪卡盘转速为3 r/min，试验过程如图1 所示。

图 1 熔覆试验过程Fig.1 Cladding experiment process

表面粗糙度测量采用比较判别法。Ra>1.6 μm 时，通过目测鉴别被测样品表面粗糙度的等级。硬度测量采用HR-150A 洛氏硬度计，选用C 标尺，测量范围为20～70HRC，采用机械-手动测试结合的测量方式。

2 正交试验及结果分析

2.1 试验方案

由于本试验待优化的工艺参数有3 个，即有3 个试验因素：激光功率、送粉速度、扫描速度。为简化试验过程，提高试验效率，采用正交试验设计[21]，该方法可通过少量次数试验来寻求最优工艺条件。本次正交试验设计有3 个因素，每个因素对应3 个水平，相应水平设置如表3 所示。

表3 工艺参数及相应水平Tab.3 Process parameters and corresponding levels

2.2 试验结果

正交试验设计9 组方案，不同组的试验参数及对应熔覆表面参数如表4 所示。

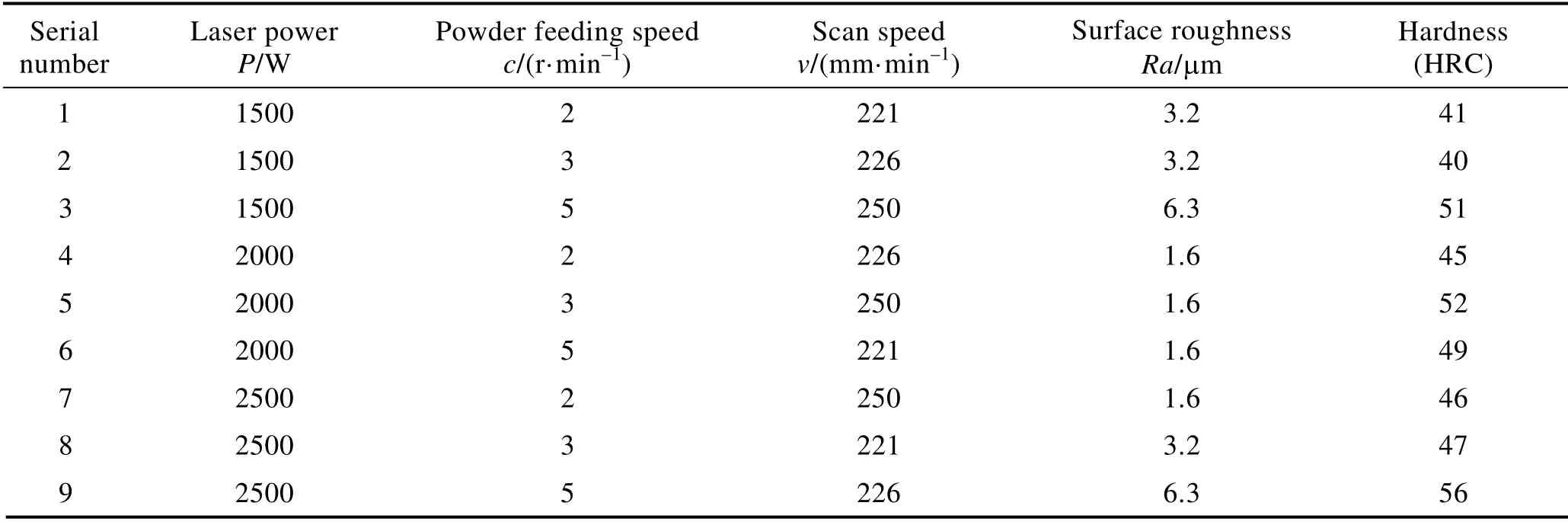
表4 L9(34)正交试验表Tab.4 L9(34) orthogonal experiment table

图2 显示了熔覆结束后的表面状况。各表面状况初步说明，熔覆层表面质量因激光功率、送粉速度、扫描速度的不同而不同。

图2 熔覆表面状况Fig.2 Surface condition of cladding

2.3 结果分析

本课题进行的正交试验有3 个因素，2 个评价指标，属于多指标试验。拟采用排队评分法进行质量指标评价，属于“综合评分法”的一种[22]。排队评分结果如表5 所示。

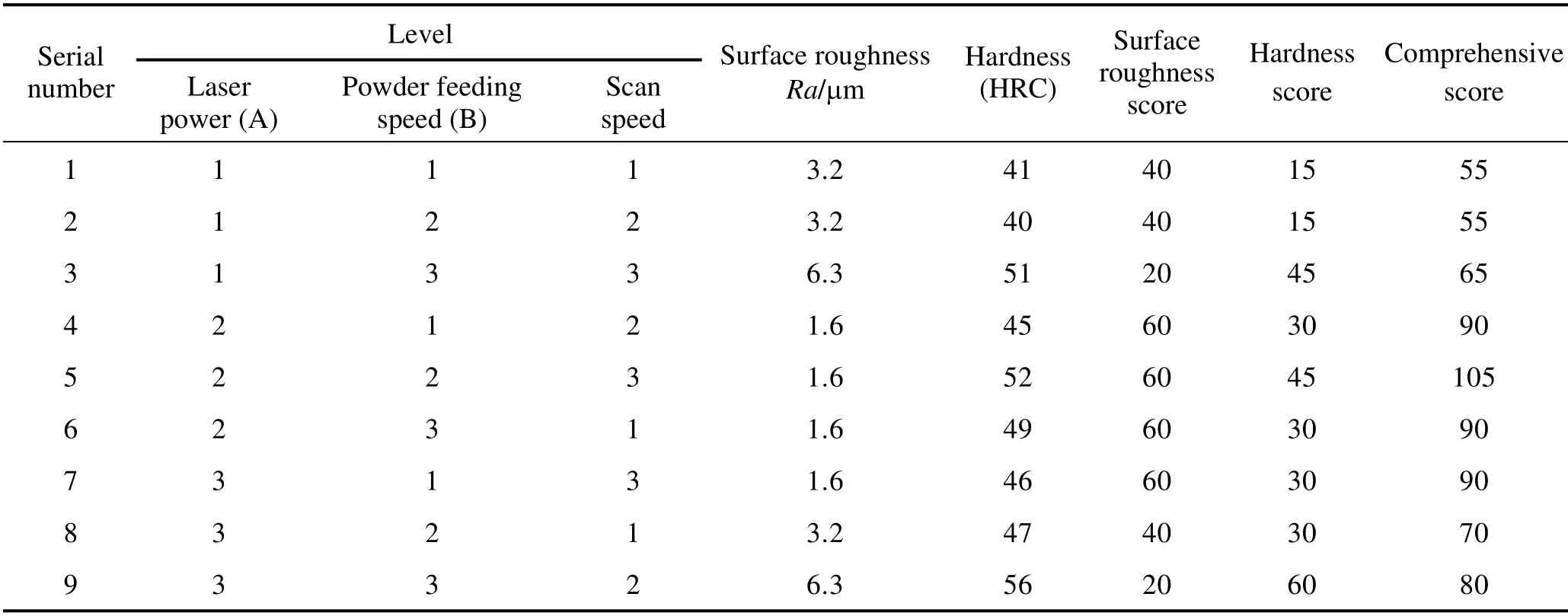
表5 排队评分表Tab.5 Queue score table

试验结果中，表面粗糙度最优值Ra=1.6 μm，最劣值Ra=6.3 μm。当表面粗糙度Ra=1.6 μm 时得分60，Ra=3.2 μm 得分40，Ra=6.32 μm 得分20。表面硬度最大值为56HRC，最小值为40HRC。规定硬度区间为[40, 45]、[45, 50]、[50, 55]、[55, 60]，对应的评分分别为15、30、45、60。将所有指标的评分值依次填入正交表中，所得结果见表5。表5 中因素A、B、C 对应的1、2、3 代表各因素的水平。

根据综合平衡法准则可得，改变激光功率对熔覆层表面质量有较为显著的影响；送粉速度对表面硬度有突出贡献，但对综合质量影响不大；扫描速度对表面粗糙度影响不大，但对表面硬度有明显影响。同时，不同的送粉速度会导致不同的优化偏向，若选择2 r/min则偏向于优化表面粗糙度，若选择5 r/min 则偏向于优化表面硬度，但是极差分析表明，它们对综合质量具有相同的优化效果。

极差分析法是正交试验的一种分析方法，其由于简单易懂、实用性强等优点而被广泛运用。极差分析时，利用公式R=max(k1,k2,k3)–min(k1,k2,k3)计算极差R值，根据极差R的大小即可判断因素A、B、C对相应评价指标的重要程度，据此获得针对该评价指标的最优方案。本次正交试验的极差分析结果如表6所示。

由表6 可知，3 个工艺参数对不同的优化指标有不同的最优参数组合。参数对熔覆层表面粗糙度的影响大小依次为：激光功率>送粉速度>扫描速度。按照表面粗糙度最小原则，最优工艺参数组合为：激光功率2000 W，送粉速度2 r/min，扫描速度221 mm/min或250 mm/min。参数对硬度的影响大小依次为：送粉速度>激光功率=扫描速度。按照硬度最大原则，最优工艺参数组合为：激光功率2500 W，送粉速度5 r/min，扫描速度250 mm/min。参数对综合质量的影响大小依次为：激光功率>扫描速度>送粉速度。综合考虑表面粗糙度和表面硬度这两个指标，选择参数优化组合为：激光功率2000 W，扫描速度250 mm/min，送粉速度2 r/min 或5 r/min。

表6 极差分析Tab.6 Range analysis

本试验考虑工艺参数对熔覆层综合质量的影响，选择其对应的最优参数组合，将其应用于实际熔覆过程，得到实际熔覆层表面状况如图3 所示。测得此时表面粗糙度为4.83 μm，硬度为52HRC，初步说明了正交试验优化设计能够高效快速地得出优化方案。

图3 正交优化熔覆表面状况Fig.3 Orthogonal optimization of cladding surface conditions

3 神经网络与NSGA-II 算法结合优化

3.1 算法优化模型描述

此优化方法的基本思想为：首先将试验数据输入神经网络，利用MATLAB 神经网络工具箱构建质量指标的预测模型；其次将神经网络的预测值作为适应度值应用到NSGA-II 算法中，进行多目标优化；最后对比实际优化结果，验算算法优化结果的有效性。

3.2 算法优化方案

对工艺参数-表面粗糙度、工艺参数-硬度分别用神经网络进行建模。由于正交试验所得数据较少，另外补充输入数据和测试数据，补充后的输入数据和测试数据及相应的熔覆层表面质量如表7、表8 所示。

表7 输入数据Tab.7 Input data

表8 测试数据Tab.8 Test data

3.3 算法优化过程及结果

图4 显示了神经网络对表面粗糙度和硬度的预测结果，可以看出误差随训练次数的增加而逐渐下降，最终达到设定值。

图4 Net-MSE 图Fig.4 Net-MSE diagram: a) surface roughness, b) hardness

图5 显示了训练结束后，神经网络分别对表面粗糙度和硬度的预测值与样本实际值对比情况。蓝色的点表示样本实际值，红色的点表示预测值。折线图表示测值和样本实际值之间的误差。

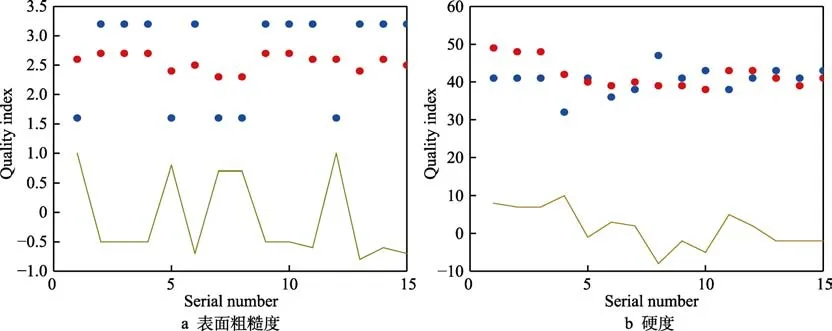
图5 预测、实际对比情况Fig.5 Forecast and actual comparison: a) surface roughness, b) hardness

使用MATLAB 的Gamultiobj 函数进行优化，参考同样运用BP-NSGAⅡ方法进行多目标优化的文献[24-27]，选择最优前端个体系数为0.1，初始种群数Population Size 为100，停止代数StallGenlimit 为100，适应度函数偏差为0.1，代码罗列如下：

经过一系列程序优化，最终结果如表9 所示。

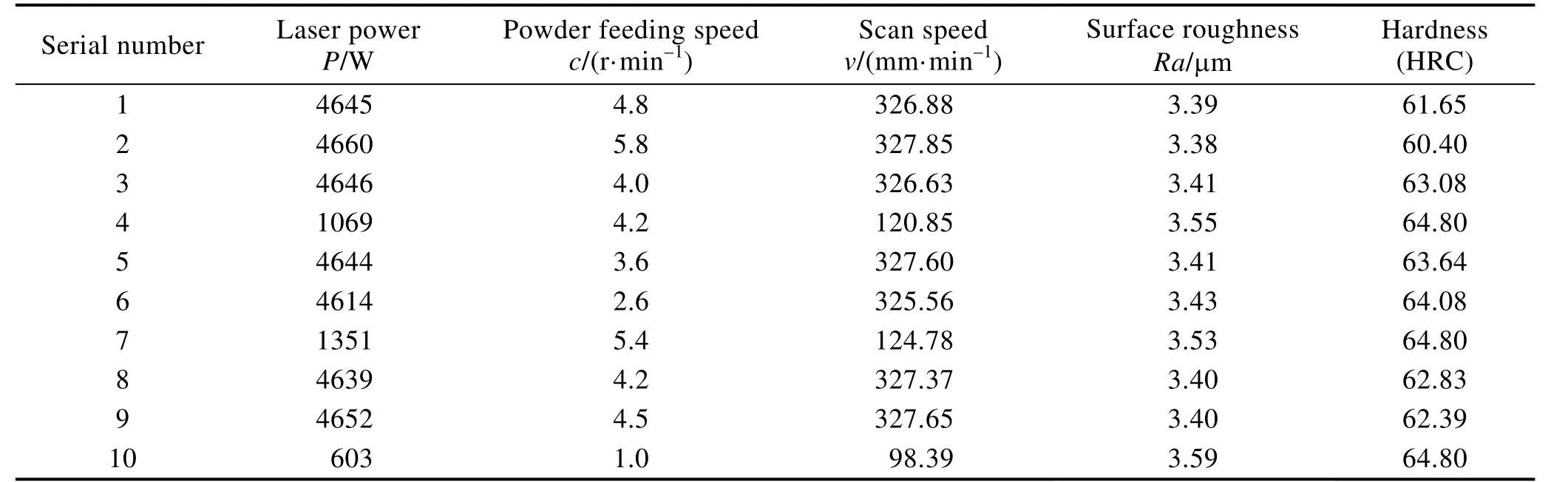
表9 优化结果Tab.9 Optimization results

3.4 算法优化分析与验证

分析表9 优化结果，所得优化解的表面粗糙度数值差别不大。根据硬度最大原则，选取最优工艺参数组合：激光功率4614 W，送粉速度2.6 r/min，扫描速度325.6 mm/min。将上述参数组合应用到实际熔覆当中，最优参数实际熔覆层表面状况如图6 所示，熔覆表面无塌陷及厚度不均等问题，直观表达了通过算法获得的最优工艺参数能大幅提高熔覆层表面质量。

图6 算法优化实际熔覆表面状况Fig.6 Algorithm to optimize the actual cladding surface condition

实际测得表面粗糙度为3.75 μm，表面硬度为59.7HRC，对比实际优化值与算法优化值，各优化指标对比情况如表10 所示。对比发现，误差为5%～10%，证实基于神经网络的NSGA-II 算法优化有效，可信度高。

表10 优化的实际值与算法值数据对比Tab.10 Comparison of optimized actual value and algorithm value data

4 优化方案分析

分别对比NSGA-II 算法实际优化的指标、正交优化的指标及优化前的指标，优化前后各参数对比情况如表11 所示。

由表11 可知，正交优化后，熔覆层表面粗糙度降低了23.3%，但硬度没有优化效果；NSGA-II 算法实际优化后，熔覆层表面粗糙度降低了40.5%，硬度提高了6.6%。对比发现，NSGA-II 算法对熔覆层质量的优化效果更好，能够更加快速、有效地获得多目标优化最优工艺参数组合。其原因主要有：1）原理上正交试验设计和分析方法通过部分试验方案反映了全面试验信息，因此试验方案较少，且数据点分配均匀。本次正交试验设计虽然高效快速，但相对于基于更多样本的NSGA-II 算法无法得到更精确的数据参数。2）实际优化过程中，正交试验设计和分析过程误差较大，且只有在试验所考察的范围内才有意义，而NSGA-II 算法在基于神经网络之后，通过改进避免了局部最小等缺点，能够获得更精确的最优解。

表11 正交优化与算法优化数据对比Tab.11 Comparison of orthogonal optimization and algorithm optimization data

5 结论

通过正交试验设计，采用排队评分法综合评价熔覆层质量，并进行极差分析，得出对熔覆层综合质量影响大小的排序依次为激光功率>扫描速度>送粉速度。在此基础上，得到的正交优化方案可使熔覆层表面粗糙度降低23.3%，但对硬度无优化效果。

利用神经网络结合NSGA-II 遗传优化算法，对比实际测量值，最终得到优化工艺参数：激光功率4614 W，送粉速度2.6 r/min，扫描速度325.6 mm/min。此条件下，表面粗糙度Ra=3.75 μm，硬度达59.7HRC。NSGA-II 算法对熔覆层表面粗糙度的优化效果较为显著，对表面硬度的优化效果一般。

基于神经网络的NSGA-II 算法的优化效果比正交优化效果更快更好。NSGA-II 优化算法对表面粗糙度的优化效果较为明显，对表面硬度的优化效果较为微弱。本试验仅简单地将目标函数加以正负变换即作为适应度函数，后续应选取多种适应度函数构造方法，比较优化结果而后选取。