隔膜压缩机曲轴的静力学及动力学分析

田金艳，张海龙

（1.中国农业大学工学院，北京 100083；2.丰电金凯威（苏州）通用机械有限公司，江苏苏州 215558）

1 引言

随着氢能源的不断发展，隔膜压缩机因其结构特殊性，在增压储氢环节得以广泛应用。隔膜压缩机主要由曲轴连杆机构和气缸组件两大部分组成。曲轴作为传动机构中的最关键零件，承受复杂的交变载荷，曲轴的使用寿命一定程度上决定了传动机构的可靠性，进而决定了压缩机的使用寿命。曲轴的强度问题是影响隔膜压缩机可靠性的一个重要因素。此外，除了曲轴的强度，若曲轴发生共振也会导致曲轴发生疲劳而失效[1]。对于此类大型机械，一旦曲轴发生失效，机器停用一段时间，会造成较大的经济损失。因此，本文对曲轴进行静力学和动力学特性分析，为曲轴的设计优化提供一定的参考依据。

本文采用ANSYS软件，结合APDL和Workbench的使用特点，对曲轴进行静力学分析，完成强度静力学校核；但静力学分析结果无法判断曲轴在整个运转周期内的应力分布情况。因此，为了更准确分析曲轴的动力学特性，首先对曲轴进行模态分析，得到各阶固有频率和振型，判断曲轴是否发生共振以及可能出现的失效形式；再对曲轴连杆机构进行刚柔耦合瞬态动力学分析，计算曲轴在一个循环周期的应力应变分布情况。

2 曲轴受力分析

隔膜压缩机的基础传动部件主要包括曲轴、连杆瓦、连杆、小头衬套、十字头销、十字头和滑道等。通过三维绘图软件绘制装配体模型见图1，各零部件的材料参数见表1。

表1 各零部件的材料参数

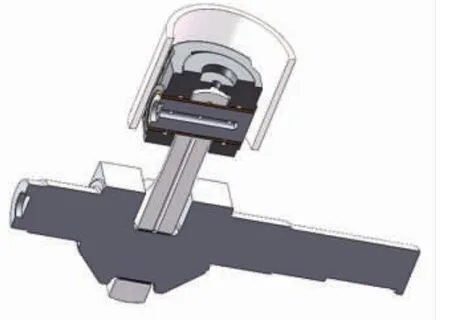
图1 装配体模型

曲轴连杆机构承受气缸部分传递的气体力、往复惯性力以及旋转惯性力，且都为与曲轴转角呈相应函数关系的变化载荷。曲轴连杆机构受力示意图如图2所示。

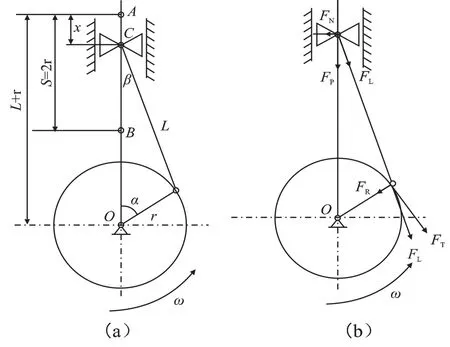
图2 曲轴连杆机构受力分析图解

此外曲轴连杆机构还承受十字头、十字头销以及连杆小头往复运动引起的往复惯性力FIs和曲柄、曲柄销以及连杆大头不平衡质量旋转引起的旋转惯性力FIr等力。

将曲轴所受力等效到曲柄销处，主要包含切向力FT、法向力FR此外，还承受由旋转质量mr引起的旋转惯性力FIr；因此曲轴的曲柄销处所受的合力为

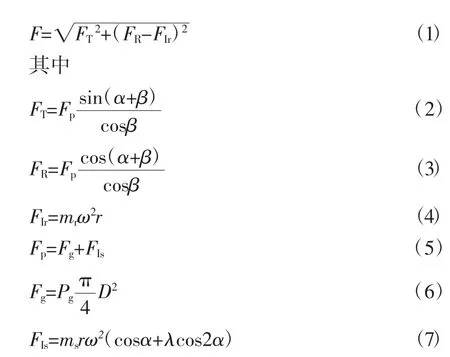
其中Fg是随压缩机的4个过程不断变化的气体力如图3，具体分以下4个过程计算。

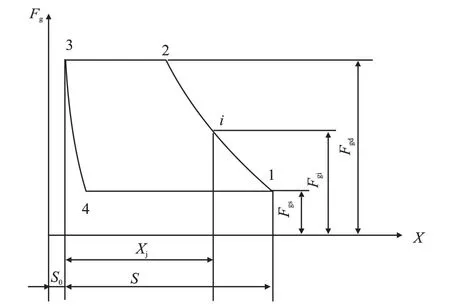
图3 气体力指示图

其中，1～2段表示压缩过程，2～3段表示排气过程，3～4段表示膨胀过程，4～1表示进气过程。

（1）膨胀过程

（2）吸气过程

（3）压缩过程

（4）排气过程

式中 pi——任意时刻的气体压力

pd′——排气终了压力

ps′——吸气终了压力

xi——任意时刻活塞的位移

S——隔膜压缩机的行程

S0——余隙容积的当量行程

m——膨胀指数

n——压缩指数

曲轴的转速为600 r/min，进气压力为12.5 MPa，排气压力为45 MPa，通过matlab编写程序，计算得到隔膜压缩机一个工作循环的随角度变化的气体力载荷数据，通过origin绘制曲线如图4。

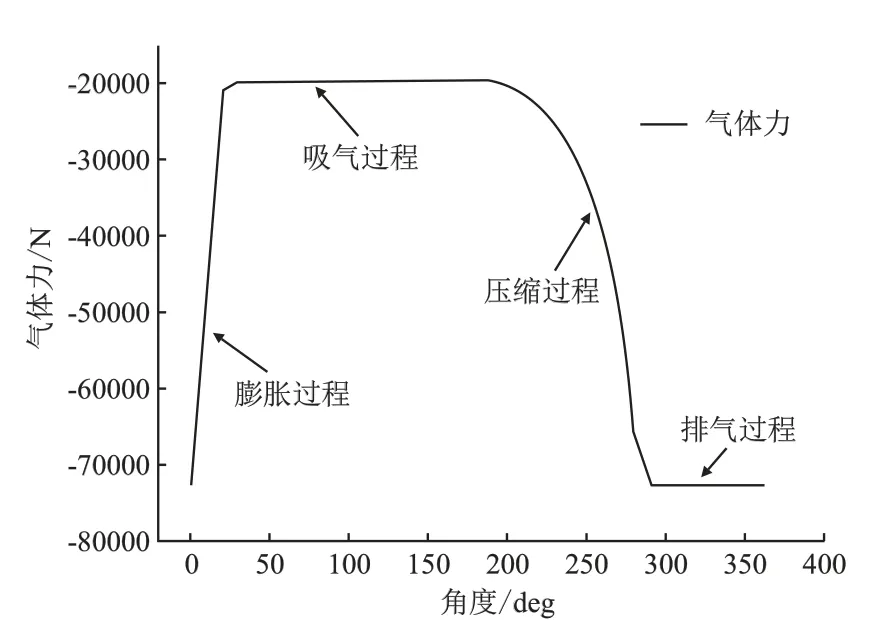
图4 隔膜压缩机一个工作循环的气体力

如图4可知，最大气体力出现在排气过程，为72661 N。

3 曲轴的静力学分析

以排气终了，气体力最大时刻为基准，将曲轴连杆传动机构中的旋转惯性力以及连杆力等效到曲轴的曲柄销上，进行静力学强度分析。参考相关文献可知，曲轴连杆机构的曲柄销受力情况分布复杂，沿着轴线方向受力呈二次抛物线分布；沿着圆周120°范围内，载荷呈余弦分布。载荷分布示意图如5所示。

因此，对曲轴进行有限元静力学分析时，通过以下函数进行边界条件的加载

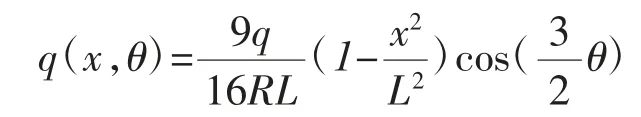
式中 L——曲柄销处曲柄销的半长

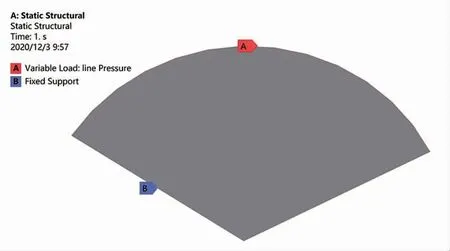
图6 圆周方向加载示意图

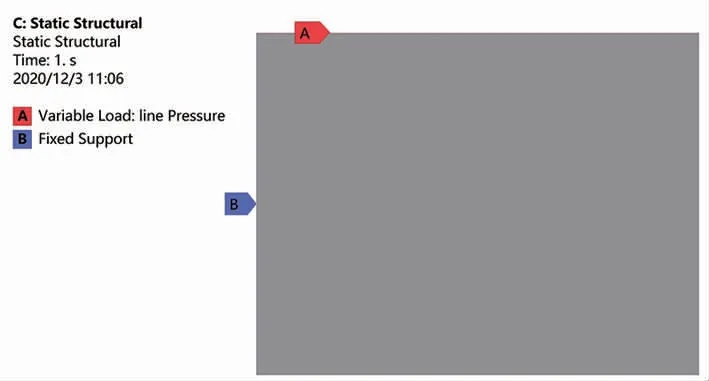
图7 轴向方向加载示意图

R——曲柄销的半径

x——曲柄销处沿曲轴轴线方向的位移，x=-L～L

θ——曲柄销处圆周方向的角度范围，

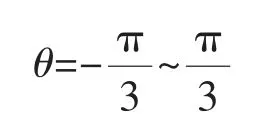
首先，通过2D模型分析，分别模拟轴向、周向的中面载荷部分，为曲轴实体模型函数加载奠定基础。最终，基于ANSYSAPDL 的命令流和Workbench进行曲轴的函数加载及求解，完成联合仿真。

3.1 2D 模型分析

（1）有限元模型的建立

通过Workbench自带DM绘图插件，绘制曲柄销轴向和周向的中面截面，定义单元类型为surf153单元，结合曲柄销周向和轴向中面的载荷分布情况，分别进行约束条件以及余弦函数载荷的加载，具体见图6、7；进行相应的求解设定，并进行求解。

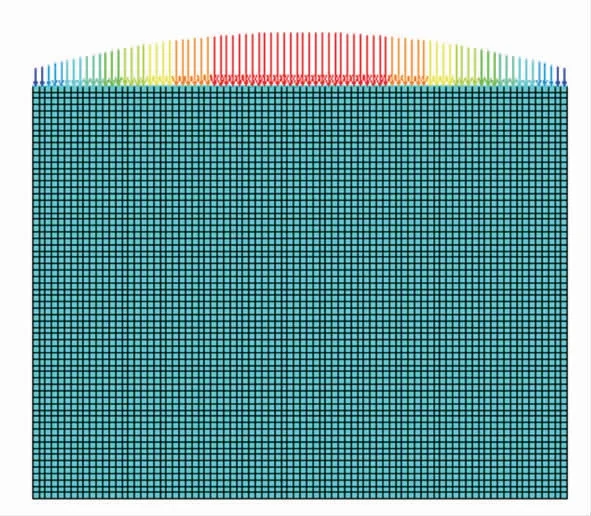
图9 轴向方向载荷分布

（2）载荷分布情况

将Workbench 加载的结果导入至Mechanical APDL，并输入相关命令流，显示载荷分布情况如图8、9所示。

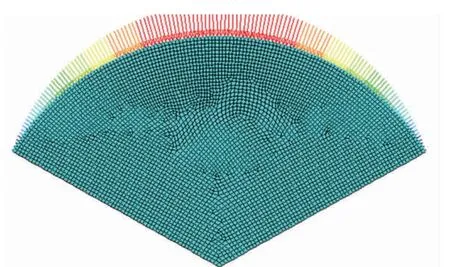
图8 圆周方向载荷分布

综上所述，仿真的载荷分布与理论载荷分布情况图5结果一致，此加载方法合理，根据其思路，可对曲轴三维模型进行函数加载。

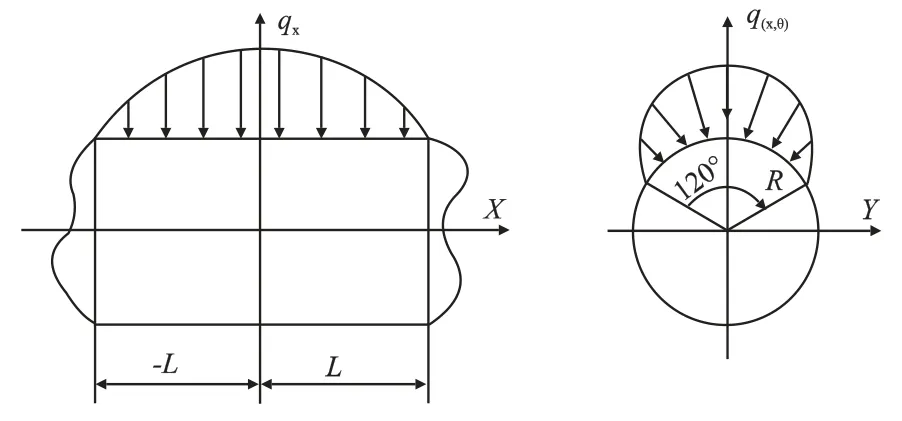
图5 曲柄销轴向、周向载荷分布示意图

3.2 曲轴3D 模型的函数加载

通过APDL的GUI操作进行函数定义并加载，导出相应的命令流文件，删除多余的程序，再将此命令流在Workbench环境中对曲柄销进行命令流函数加载并求解。

（1）有限元系统的建立

（a）进行材料设定及赋予：材料参数见表1；

（b）划分网格；

因结构较为复杂，采用PatchConformingMethod算法，进行四面体网格划分，并对过渡处进行网格细分，网格单元为Solid187，网格节点数为132375，网格单元数为90098，OrthogonalQuality达到0.8577，网格质量较好。

（c）进行约束条件和函数载荷的加载。

根据隔膜压缩机中曲轴实际约束条件，即主轴颈处通过滑动轴承连接，通过3阻尼弹簧单元模拟轴承约束，支撑刚度与主轴承刚度的参数设定为一致，即6×107N/mm；端盖约束曲轴的轴向位移，将曲轴的输入端约束轴向位移，因考虑到压缩机实际运转过程中曲轴受热的膨胀过程轴向会有一定的伸缩量，因此，将曲轴的另一端自由度释放，在该自由端施加圆柱约束，约束径向位移。

通过命令流函数载荷加载，模拟曲柄销处复杂分布的载荷，以排气过程的最大气体力载荷为基准，通过上述计算公式（1～10）计算此时刻的往复惯性力、旋转惯性力、综合活塞力、曲柄销切向力、法向力、曲柄销总受力以及曲柄销处合力载荷见表2，通过命令流将函数载荷加载至曲柄销圆周方向120°范围内，见图10并进行求解设定及求解。

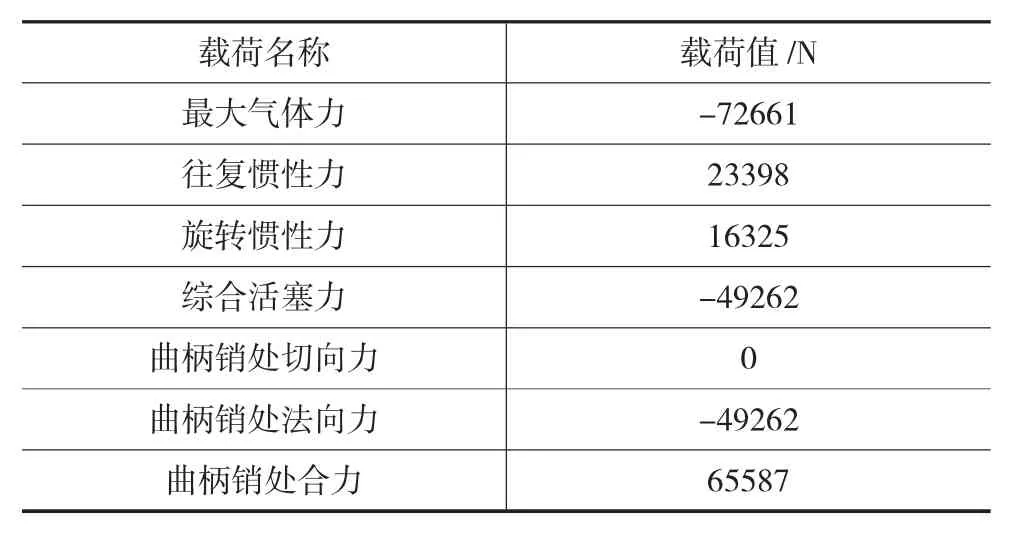
表2 排气终了时刻的各个载荷值

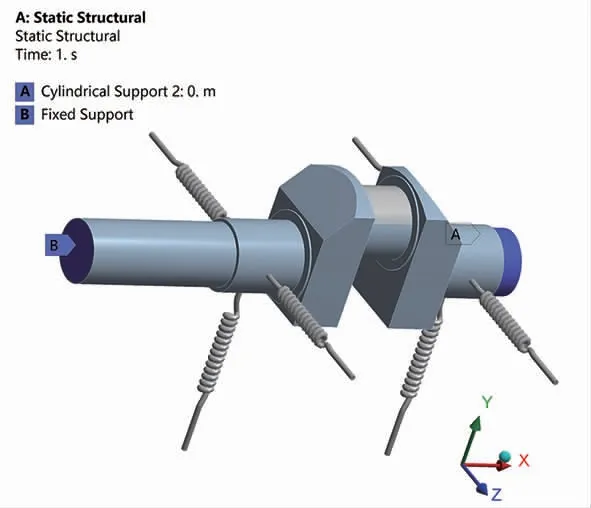
图10 曲轴加载情况示意图

（2）结果后处理

（a）载荷分布情况

将Workbench得到的结果导入至APDL界面进行载荷分布的查看，载荷分布图见图11、12，其载荷分布正确，因此，证明命令流加载合理。

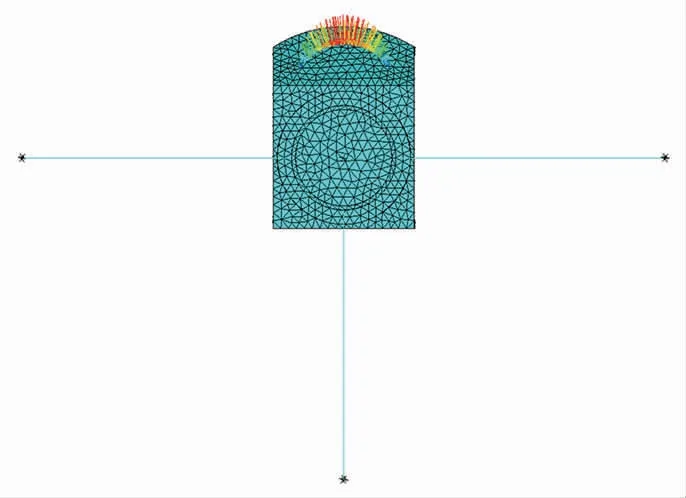
图11 曲柄销处圆周方向载荷分布

（b）结果分析

曲轴的变形和应力云图如图13、14所示。

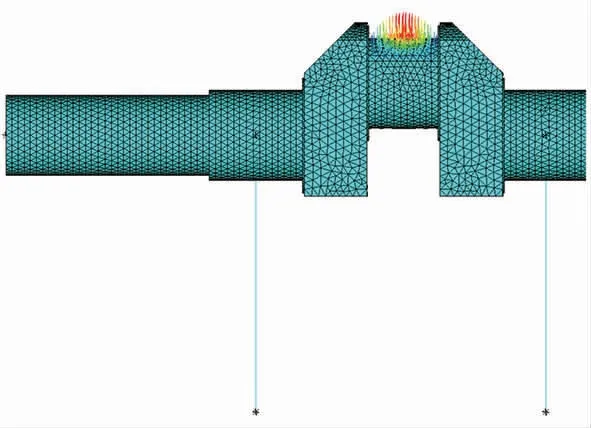
图12 曲柄销处轴线方向载荷分布

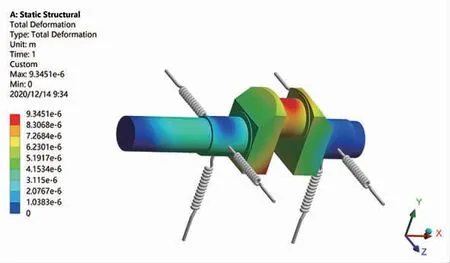
图13 曲轴的变形云图

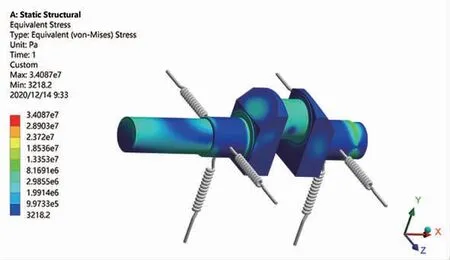
图14 曲轴的应力云图

由结果图可知，在曲柄与曲轴的主轴颈、曲柄销的过渡圆角处出现应力集中，在设计时应重点考虑此问题。曲轴的最大应力值达到34 MPa，远小于曲轴的屈服强度，因此满足强度需求。然而，静力学分析对实际运转中遇到的冲击等工况进行了忽略，无法确定整个运转周期的应力分布情况。因此，对曲轴进行模态及多体动力学特性分析。

4 曲轴的模态分析

模态分析是一系列动力学分析的基础，可通过得到结构的固有频率和振型，判断是否发生共振以及可能出现的失效形式，指导研发人员对结构进行优化。

4.1 曲轴的自由模态

通过ANSYS Workbench软件导入CAD模型，并进行材料设定及赋予；通过Modal模块进行自由模态分析，不设定任何外部载荷及约束，进行模态分析求解。

4.2 曲轴的约束模态

为接近曲轴的真实工况的模态分析结果，施加与静力学分析相同的约束条件，即将曲轴的输入端约束轴向位移；自由端添加圆柱约束，约束径向位移；通过三阻尼弹簧单元模拟轴承约束，进行前10阶模态分析。

4.3 结果对比分析

曲轴的振动主要与低阶激励频率相关，且自由模态分析的前6阶接近于0，为刚体运动部分，因此，提取了自由模态非零的前6阶模态结果（即7～12阶）以及约束模态的前6阶结果如表3所示。

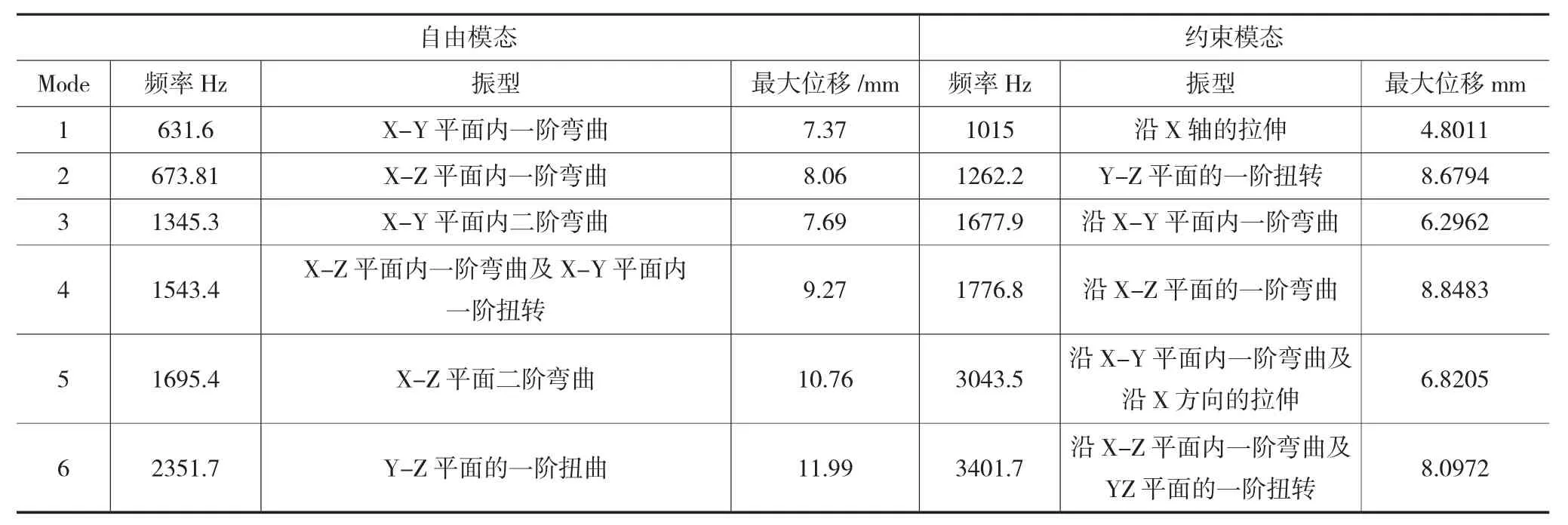
表3 模态分析结果对比

约束模态的1～6阶振型图如图15所示。

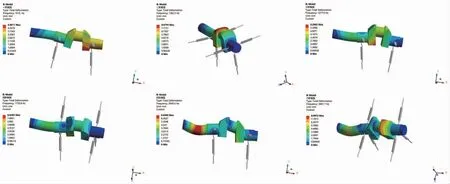
图15 约束模态的1～6 阶振型图

由上述结果对比可得，约束模态的固有频率相对于自由模态的固有频率较大。根据振型可知，多数情况下，最大变形表现为曲轴的弯曲现象。由表3可知，在约束条件下，曲轴的最小固有频率为1015 Hz，某型号隔膜压缩机曲轴转速600 r/min，在运转工况下，转动基频为62.8 Hz，曲轴的最小固有频率远大于转动基频，因此，避免了共振。

5 曲轴连杆机构瞬态动力学分析

5.1 有限元模型的建立

导入图1的装配体模型，并参照表1进行各个零件的材料定义。

5.2 边界条件的设定

为减少计算量，进行刚柔耦合瞬态动力学分析，将模拟滑道刚性化，将重要零部件曲轴、连杆、十字头销等进行柔性化。根据隔膜压缩机曲轴连杆传动机构实际运动工况，通过ANSYS软件的运动副模拟各零部件之间的运动关系，具体如下：

（1）曲轴输入端与大地建立转动副；

（2）曲柄销和连杆瓦内圈建立转动副；

（3）连杆瓦内圈与连杆瓦外圈建立固定副；

（4）连杆瓦外圈与连杆大头建立固定副；

（5）连杆小头和小头衬套建立固定副；

（6）十字头销与连杆小头衬套以及十字头衬套建立转动副；

（7）十字头衬套与十字头建立转动副；

（8）十字头与外部滑道建立移动副；

（9）外部滑道与大地建立固定副。

曲轴连杆机构主要承受气体力、往复惯性力和旋转惯性力等作用，惯性力在多体动力学分析时，软件会自动加入。因此，在ANSYS动力学分析载荷设定界面，只需设定气体力即可。曲轴转速600 r/min，一个周期为0.1 s。因此，将上述计算的一个循环周期的气体力载荷值通过表格对应加载，并进行动力学分析。

5.3 结果分析

为减少结果存储空间，每隔0.008333 s（即每隔30°）输出结果，以下为曲轴分别转过30°、90°、180°、270°以及360°度时的应力分布情况如图16～20。

表4 各个角度的时间及载荷对应值

图16 曲轴转过30°

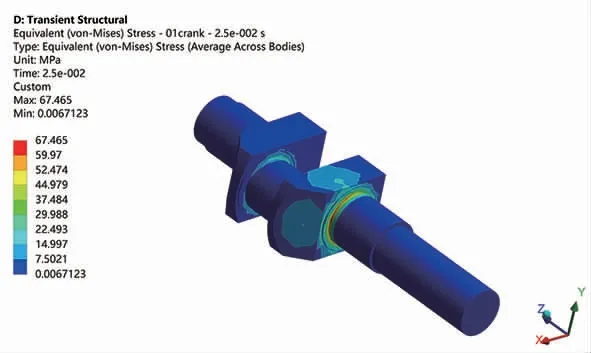
图17 曲轴转过90°

图18 曲轴转过180°

由以上曲轴转过各个角度的应力云图分布可知，最大应力主要发生在1、2、3以及4等部位，且在曲轴转过30°（即0.008333 s）时各个部位相对于其他角度都达到最大值，其中部位1的最大应力值高于其他几个危险部位，为曲轴最容易发生失效的部位，设计优化时应重点考虑如图21～23。

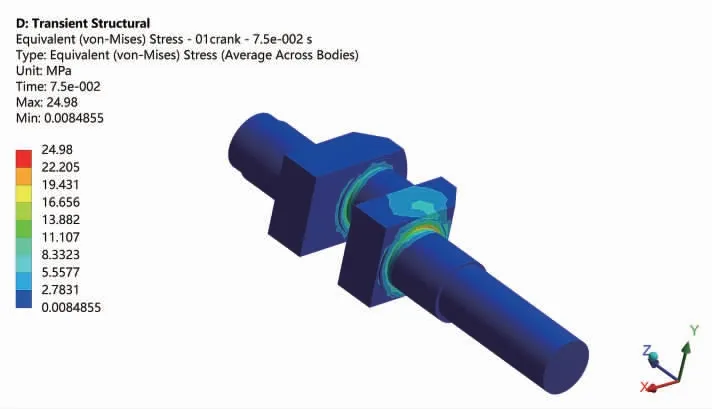
图19 曲轴转过270°

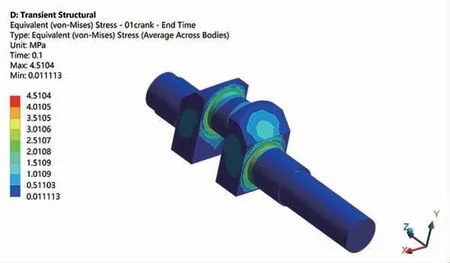
图20 曲轴转过360°

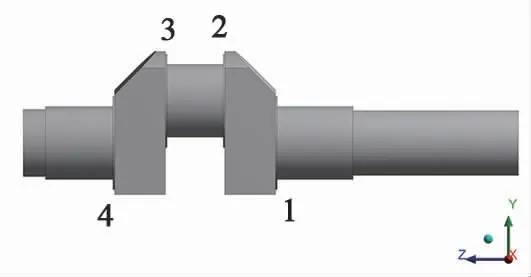
图21 危险部位示意图

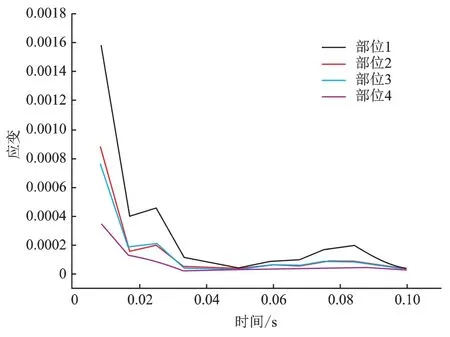
图22 危险截面的应变

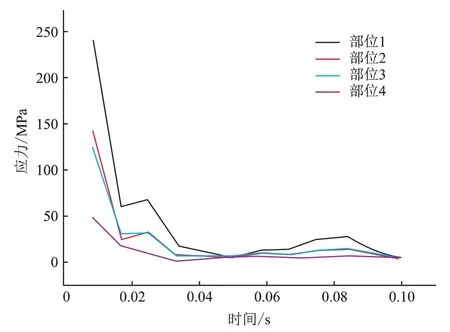
图23 危险截面的应力

6 结论

首先，基于APDL和Workbench联合对曲轴在最大压力载荷下，进行了静力学强度分析，得到的载荷分布情况与理论分布结果一致，证明命令流函数加载合理，应力分布结果表明在曲柄和曲柄销以及主轴颈过渡处出现应力集中，设计时应重点考虑；其次，对曲轴分别进行了自由模态和约束模态分析，结果表明，约束模态的固有频率比自由模态的大，最小固有频率远大于曲轴的转动基频，避免了共振的产生，且其振型多表现为弯曲变形。最后，为更准确模拟曲轴在实际运转过程中的受力情况，对曲轴连杆机构进行装配体动力学分析，结果表明，曲轴在转过各个不同角度，应力最大值主要出现在1～4个部位，且最大应力主要集中在部位1。因此，此处最容易导致曲轴的疲劳失效等问题，为曲轴的结构优化改进提供参考依据。