多中继协作空间调制的中继选择及性能分析

李 彤，仇润鹤*

（1.东华大学信息科学与技术学院，上海 201620；2.数字化纺织服装技术教育部工程研究中心（东华大学），上海 201620）

0 引言

随着第五代移动通信（5G）技术的快速发展，多输入多输出（Multiple-Input Multiple-Output，MIMO）系统由于其能够有效提高系统的传输速率且不会使用额外的带宽而得到了广泛应用［1］。然而MIMO 在给我们带来各种增益的同时，由于其系统需要同时激活多根天线，因此存在如信道间干扰、天线间同步等问题［2］；而且为了保证MIMO 系统的分集增益，还要求接收天线的数量应大于发射天线的数量，这会导致成本升高，实际应用也会较复杂［3］。为了克服上述传统MIMO 系统的不足，近年来提出了一种被称为空间调制（Spatial Modulation，SM）的多天线MIMO 方案［4］。在SM 系统中，每一时隙仅激活一根发射天线，因此在发射端仅需要一个射频单元用来进行数据传输，这样能够有效避免传统MIMO 系统中信道间干扰、天线间同步等问题，且发射天线数也可以大于接收天线数，能够达到更好的系统性能。协作通信作为一种虚拟的MIMO 技术，可以获得更高的吞吐量、更好的可靠性以及更大的通信覆盖率［5］。利用协作通信技术，在接收端能够收到来自多条链路传输的相同信号，实现空间分集。目前协作通信的中继传输协议有放大转发（Amplify Forward，AF）、解码转发（Decode-Forward，DF）、增量中继协议等。将空间调制技术与协作通信相结合，不仅能够避免传统MIMO 系统中存在的不足，还可以增大系统的分集增益，增加传输面积、速度和性能，提高信息传输的可靠性［6］。文献［7］中分析了使用DF 中继的协作空间调制系统的性能，其中每一个节点均配置为多天线；文献［8］中则在前文的基础上分别推导出了多天线AF 中继和DF中继协作空间调制系统的误比特率（Bit Error Rate，BER）性能，证明使用空间调制的系统与普通MIMO 系统相比有更高的传输可靠性。文献［9］中在分析AF中继协作空间调制系统的基础上，还对源节点和发射节点提出了一种次优功率分配方案，仿真结果表明进行功率分配的系统能够拥有更低的误码率，且所提出的次优功率分配方案效果与最优功率分配效果相近，但复杂度更低。前面的研究多是假设目的节点已经完全了解信道状态信息，且信道服从瑞利衰落，而实际情况下信道状态更加复杂，因此文献［10］和文献［11］中分别给出了在不完全信道状态信息和空间相关信道下的AF 中继协作空间调制系统的误码率性能。

当系统中存在多个中继时，除了以上分析外还涉及中继选择的问题：既可以让全部中继参与转发，增加系统的复用增益；也可以从中选择满足要求的一个或多个中继进行转发，降低系统的复杂度。文献［12］中分析了空间移位键控系统在存在多AF 中继和多DF 中继时的误比特率，当文献所提出系统使用AF中继时，中继放大接收到的信号并以循环的方式转发到目的节点，此时每一个中继节点均参与协作；当使用DF 中继时，仅正确检测到源节点信号的中继才能将信号转发给目的节点。文献［13-14］中分别分析了正交空间调制系统在多AF 中继和多DF 中继协作时的误比特率，将要传输的信息比特分为四部分：一部分用于选择中继，一部分用于调制信号，其余两部分分别用于选择传输调制信号实部和虚部的两根天线，在每一时隙仅激活一个中继。文献［15］中提出了一种多DF 中继的空间调制系统，选择出可以正确解码的DF 中继形成中继簇，再次进行空间调制后进行发送。综上所述，现有文献中多AF 中继协作空间调制系统用于对中继进行选择的方法主要是所有中继循环转发或者随机选择中继转发。

目前有关多中继协作通信系统的研究多与传统MIMO、蜂窝网络系统等相结合，但与空间调制技术相结合的较少，且这些论文多考虑的是源节点到中继和中继到目的节点间距离相等的情况，当多个中继节点处于源节点和目的节点间不同位置时，文献［12］中所使用的中继节点循环转发或文献［13］中的使用传输比特信息中的一部分来随机选择中继的方法显然不适用，因为若选择到信道系数不理想的中继，则系统误码率将增大，传输性能变差。且文献［13］中提出的使用lb(N)（N为中继数量）比特来选择中继的方法在中继数量上也存在局限性，系统中中继数量必须为2的对数。

基于以上分析，本文将空间调制技术与协作通信相结合。在源节点使用空间调制技术，分别向多个处于不同位置的AF中继和目的节点发送数据，在中继处基于节点位置信息对全部中继进行选择，选择最接近源节点和目的节点间中点位置，即等效信道增益最大的中继进行放大转发，目的节点使用基于最大似然的最优解调方法来恢复出选择的天线序号和调制信号。最后运用矩生成函数法分析系统的理论误比特率，并对该理论结果进行了仿真验证。

1 系统模型

本文提出的多中继选择空间调制系统的系统模型如图1所示，这是一个工作在半双工模式下的源节点使用空间调制的多AF中继协作三节点通信系统模型，图中Ri表示中继。

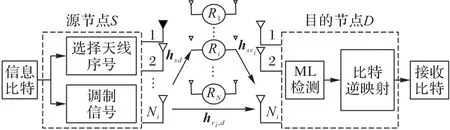
图1 多中继选择空间调制系统的系统模型Fig.1 System model of multi-relay selective SM system

该系统模型由一个源节点(S)、一个目的节点(D)和N个工作在AF 协议下的中继节点(Ri)组成，源节点和目的节点各自配置有Nt、Nr根天线。在后文中为简化计算，令发射端具有两根发射天线，接收端具有两根接收天线，即Nt=Nr=2，而中继只包含一根接收天线和一根发射天线，即且该N个中继与源节点的距离不等，即它们的各不相同，但均满足，其中dsd表示源节点至目的节点的距离表示源节点至所选中继的距离，表示所选中继至目的节点的距离。假设中继节点已知自己的信道状态信息，目的节点都已知全部完整信道状态信息，且所有节点间距离均已知。该系统模型包括两条通信链路：其中一条为直接链路S-D，即源节点发送的信号直接传输到目的节点，不经过中继转发；另一条为放大转发中继协作的通信链路S-R-D，即源节点发送的信号被中继接收后，经过放大转发中继放大后再转发给目的节点。假设任意两节点间均为独立的平坦瑞利衰落信道，信道矩阵分别为信道矩阵内各元素均是零均值的复高斯随机变量，在一个传输时隙中保持不变。所有信道噪声分布相同，均为独立的零均值、方差为N0的复高斯随机变量。

在该系统中，对源节点使用空间调制技术，每时隙在全部发射天线中仅激活一根天线，用于承载调制后的信息。因此将发送的比特流分为两个部分：一部分用于进行符号调制，另一部分用于选择天线。故调制后的符号可通过所选择的天线来从源节点进行传输，每一时隙所发送的符号矢量为：

其中：xq为的第l个元素，l为所激活的天线序号。

由于图1 所提出的三节点系统模型工作在半双工模式下，在该工作模式中，一组数据需要通过两个时隙由源节点向目的节点传输，对图1 的系统模型进行简化，用三节点描述该组数据的传输过程如图2所示。其中：xlq为源节点发送矢量，ysd为源节点发送、目的节点接收到的信号为源节点发送、中继节点接收到的信号为中继节点转发、目的节点接收到的信号。

图2 数据传输过程Fig.2 Data transmission process

在第一时隙，源节点首先将需要发送的比特流一部分进行调制，得到xq，并将其映射到另一部分比特流所选择激活的天线l上，形成发送矢量xlq，分别传输给目的节点和基于全部中继节点所处的位置在N个中继节点中选择出位置最接近源节点和目的节点间中点的第i个中继。因此在这一时隙中目的节点接收到的信号ysd和中继节点接收到的信号可以分别表示为：

在第二时隙，被选中的第i个中继节点对第一阶段接收到的来自源节点的信号ysri进行放大后再将其转发至目的节点，节点放大系数Ai可表示为Ai=，式中i表示所选择的中继序号，Pr和Ps分别表示中继节点和源节点的发射功率，假设所有的中继节点发射功率相同，均为为源节点和中继节点间信道系数分布的方差，N0为噪声方差。此时目的节点接收到的来自中继放大后的信号可以表示为：

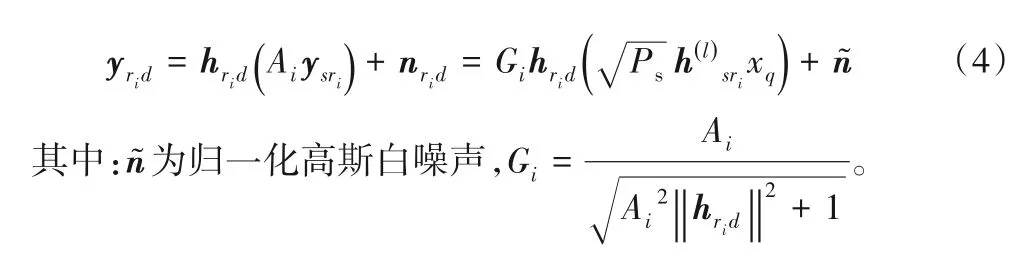
图1 所示的系统在目的节点处基于最大似然检测算法，对目的节点接收的信号进行接收解调，对选择的天线序号和星座符号进行联合检测［16］，最终解调出的天线序号和星座调制符号可表示为：

2 误比特率性能分析

本章将对前文所提出的多中继协作空间调制系统的理论误比特率进行分析。假设源节点所激活的天线序号和发送的调制符号为λ(l，xq)，目的节点检测得到的天线序号和调制符号的估计值为可以得出该系统的条件成对错误概率如式（6）：

其中：Pr(·)表示概率，Q(·)为Q函数。

令 式（6）的 Q 函数内根号下的γsd=为直接链路S-D 的瞬时信噪比，γsrid=为中继协作链路S-R-D的瞬时信噪比，对式（6）进行化简与计算可以得到该系统的成对错误概率如式（7）：

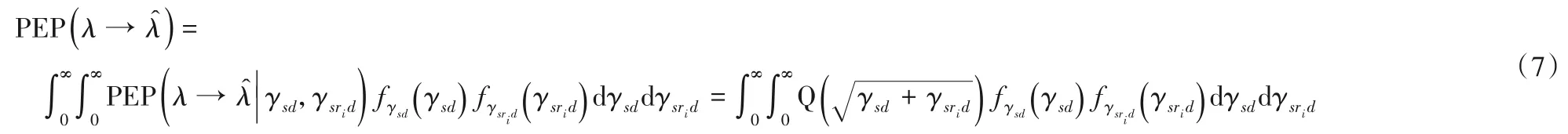
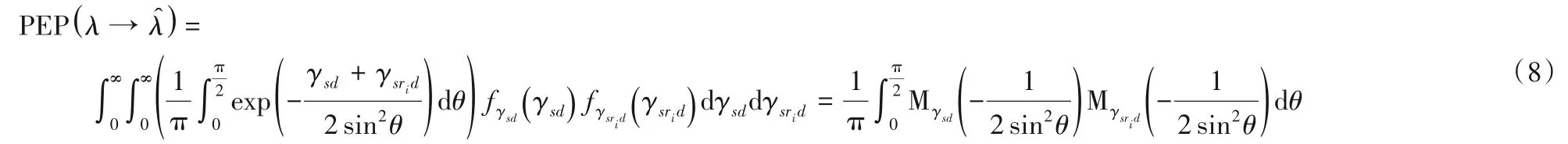
由以上推导可知，该系统的平均成对错误概率可由其系统中两条链路的矩生成函数之积来得出，因此以下将分别对这两条链路的矩生成函数进行分析。

2.1 S-D链路瞬时信噪比的矩生成函数Mγsd(s)

2.2 S-R-D链路瞬时信噪比的矩生成函数

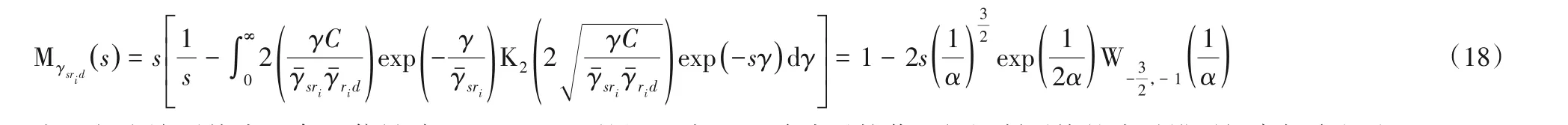
由此得出该系统中两条通信链路S-D 和S-R-D 的矩生成函数可表示为式（12）和式（18），将它们代入式（9）中，可得此多中继协作空间调制系统的成对错误概率如式（19）：

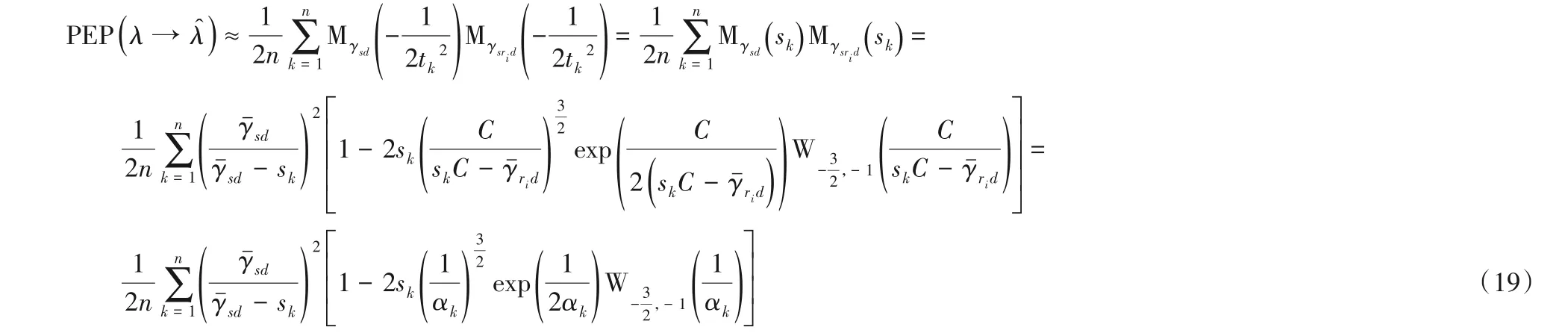
由文献［13］中的式（21）已知，AF 中继协作空间调制系统的理论误比特率可表示为以下的上界：

将式（19）中得到的系统成对错误概率代入式（20），最终可以得到该基于位置对全部中继进行选择的多中继协作空间调制系统的理论误比特率为：

3 次优中继选择

在该系统中，中继采用AF中继协议进行转发。考虑到尽量降低系统的复杂程度，当系统中存在任意数量个不同位置的AF中继时，在单个中继节点完全能够承担系统中协作转发任务的条件下，每时隙只需从多个位置不同的中继节点中选择一个最接近最优位置的中继即可；且当系统中存在多个中继时，传统的中继选择方法如所有中继节点循环转发或者随机选择的方法，由于不考虑中继所处位置的影响，在选择时可能会选择到位置不佳的中继，对系统的误比特率造成影响，因此本文提出了一种考虑中继位置的中继选择方法，并在本章对所提出的方法进行理论分析和实验验证。

3.1 理论分析

从文献［20］中可知，为降低系统的误比特率，应选择等效信道增益较大的中继进行放大转发。以降低系统的误比特率为目标，为使接收端信噪比γ=最大，通过前文中已知的信噪比γsd和对接收端信噪比γ求平均后根据数-距离的路径损耗模型，令等效信道增益为：

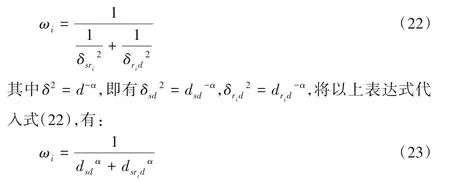
从信号衰落的角度来看，当中继距离源节点或目的节点其中一方较近时，和另一方的距离就会较远，此时较远的距离传递信号会遭受严重的路径损耗。中继协作S-R-D 链路的信噪比取决于S-R 链路以及R-D 链路的质量，其中任何一个链路的路径损耗严重都会影响系统的整体性能；而当中继位于源节点和目的节点中间时，S-R 和R-D 的距离相等，不会出现一方存在严重的路径损耗，此时系统的误比特率最低。

因此所提出的中继选择方法的重点即为选择出全部中继中最接近最优位置的中继进行放大转发。假设节点均已知自身位置，所提出的中继选择方法具体步骤如下：

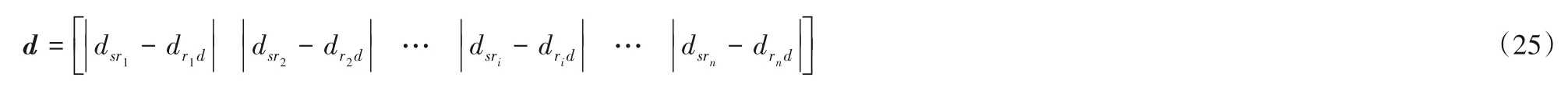
3）行矩阵d中的最小值即表示中继和源节点间距离以及中继和目的节点间距离的值最接近，此时该中继即为本中继选择方法所选中的次优中继，中继序号可表示为：

式中：R表示选择的中继序号，d为距离矩阵，n为带选择的全部中继数量。

3.2 实验验证

对单个AF中继协作SM系统在中继处于源节点和目的节点间不同位置的情况下使用Matlab 进行仿真实验，规定源节点和目的节点间距离为1，考虑瑞利衰落信道，使用正交相移键控（Quadrature Phase Shift Keying，QPSK）调制，源节点和中继间距离取值为1/2、1/4、1/6、1/8。仿真模型如图3（a）所示，仿真实验结果如图3（b）所示。从图中可以看出，当中继处于源节点和目的节点中间的位置，即=1/2时，系统的误比特率最低，且误比特率随着两者间距离的减少而增加，故称=1/2 此时的中继为最优位置中继，即源节点和中继间距离越接近源节点和目的节点间距离dsd的一半越好，此时源节点和中继间距离与中继和目的节点间距离最接近，也就是满足最小。

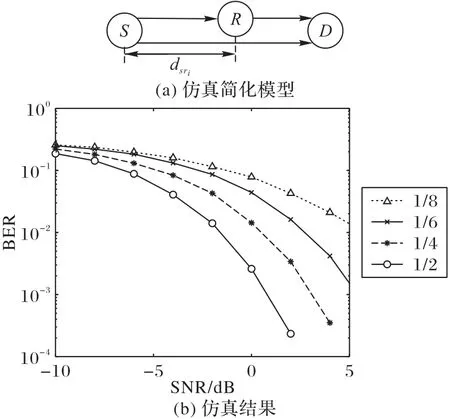
图3 单中继协作SM系统仿真Fig.3 Simulation of single relay cooperative SM system

4 仿真结果及性能分析

使用Matlab 对本文所提出的多AF 中继协作空间调制系统的误比特率进行仿真验证。在源节点使用空间调制技术，考虑瑞利衰落信道，假设各节点间距离均已知，源节点和目的节点间距离规定为1，中继均匀分布于两节点之间。源节点发射天线数目Nt=2，目的节点接收天线数目Nr=2，中继发射天线数目=1，接收天线数目=1，调制方式为二进制相移键控（Binary Phase Shift Keying，BPSK）和QPSK，中继数量为0、1、4，信道间衰落系数α=5，信号带宽为单位带宽。

图4 分别给出了中继数量为0、1、4 时空间调制系统误比特率的仿真值和理论值对比。使用QPSK 调制，目的节点接收天线数目Nr=2，单中继系统中继位于源节点和目的节点间中点位置（即=1/2），即最优位置的中继，多中继系统包含四个中继，均匀分布于源节点和目的节点之间。由图可看出无论中继的个数是多少，采用AF中继协作空间调制系统的误比特率均低于无中继协作的系统。且当系统采用本文提出的基于中继位置的方法进行中继选择时，仿真得出的误比特率与中继位置处于两节点间中点的单中继系统的误比特率相近，这是因为使用本文所采用的中继选择方法所选择的中继是所有处于不同位置的中继中位置最接近=1/2 的中继。故当系统中存在多个不同位置中继时，使用本文所提出的方法也可以选择出最接近最优位置的中继，得到与其相近的性能。图中的实线表示仿真结果，虚线表示理论误码率，仿真曲线和理论曲线之间的微小误差是由式（9）省略的余项以及式（21）的上界带来的。可看出两曲线较吻合，证明计算结果的准确性。

图4 中继数量对系统性能的影响Fig.4 Influence of number of relays on system performance

图5 给出了本文所使用的中继选择方法与文献［12］中所采用的所有中继循环转发及文献［13］中所采用的随机选择中继方法的对比。使用QPSK 调制，目的节点接收天线数目Nr=2。图中可以看出，随着信噪比的增大，误码率呈下降趋势，且本文选择出的最接近最优位置的次优中继误比特率要优于另外两种常见的中继选择方法。这是因为在位置不同时，另外两种方法由于无法保证能够选择到接近最优位置的中继，可能会造成中继等效信道增益不佳，从而影响系统的误比特率性能。

图5 中继选择方法对系统性能的影响Fig.5 Influence of relay selection method on system performance

图6 给出了本文所提出的多中继协作空间调制系统在使用不同调制方法以及不同数目接收天线的情况下的误比特率的曲线。中继数N=4，分别令调制阶数M=2（BPSK）或M=4（QPSK），目的节点接收天线数目Nr为2或4，此时可以看出调制阶数和接收天线的数目均会对系统的误比特率带来影响。在接收天线数目相同的时候，采用BPSK 调制的系统的误比特率要低于采用QPSK 的系统。这是因为当调制阶数增大时，相邻星座点之间的欧氏距离减小，解调时会更加容易产生错误，导致误比特率增高。在调制阶数相同的时候，接收天线数目为4 时系统误比特率与接收天线数目为2 时相比较低。这是因为系统的分集增益受限制于接收天线的数目，随着接收天线数目的增多，系统所获得的分集增益也越多，接收端能够得到更多来自不同链路所传输的信号，误比特率会降低。且当接收天线数目相同时，较高信噪比下误比特率曲线的斜率也趋于一致，因此也可以看出系统的分集增益由接收天线的数目所决定。

图6 调制阶数和接收天线数目对系统误比特率性能的影响Fig.6 Influence of modulation order and the number of receiving antennas on system BER performance

5 结语

本文将空间调制与协作通信相结合，提出了一种多中继协作空间调制方案，选择最接近最优位置的中继进行转发，并对该方案在瑞利衰落信道下的性能进行了分析。推导出了各链路的瞬时信噪比的矩生成函数，并进一步推导出了多中继协作空间调制系统的成对错误概率解的表达式和平均误比特率的上界。仿真结果表明本文所提出的多中继空间调制方案在中继处于不同位置时也可以获得较好的性能。本文模型考虑的是简单的瑞利衰落信道，且所有节点都已经知道完整信道状态信息，但在实际情况中存在多种类型的信道且信道状态复杂，因此考虑不完全信道状态信息下的多中继协作空间调制系统将是未来研究的方向