基于图卷积与长短期记忆网络的动态网络表示学习模型

张元钧，张曦煌

（江南大学人工智能与计算机学院，江苏无锡 214002）

0 引言

随着大数据时代的到来，数据信息急剧增加，而且各种数据之间存在千丝万缕的关系，因此复杂信息网络普遍被用来存储实体间复杂的关系信息，而事物之间的联系可以自然地用图数据的形式表示。比如学术论文之间的引用和被引用关系可以看作网络中的边，各类论文便是网络中的各个节点，由此学术论文之间的引用关系就可以用图数据集的形式表示成相应的复杂网络；社交媒体［1］中的用户可以看作网络中的节点，用户之间的联系是相对应的边，由此形成了社交网络；城市交通中的城市即为网络中的节点，道路的通畅情况可作为网络中的边，由此形成了交通网络。上述三个复杂网络案例都是经典的动态网络，随着时间的推移，边之间的联系也会不断变化。链路预测的主要目的是预测未来网络中丢失的边，或者可能出现的边。近年来，大数据和深度学习技术日渐成熟，上述交通网络中可以通过分析前段时间的道路拥堵情况来判断未来时刻交通的畅通情况，类似此种应用的广泛增加，因此复杂信息网络的链路预测［2］已经成为一个热门的研究课题。

大数据时代下，网络被用来存储事物间复杂的关系信息，将复杂的网络信息表示成相应的拓扑图结构，提取拓扑图的信息与时间之间的联系，来预测未来时刻节点之间的链路关系。以图1 所示的简单社交网络为例，模拟链路预测模型提取特征的一些方法。

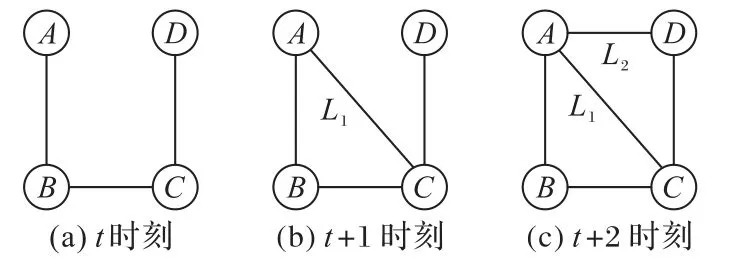
图1 社交关系网络演变图Fig.1 Social network evolution diagram

图1中，A、B、C、D分别代表四名用户，用户之间出现的连线表示用户之间相互认识，没有连线则彼此不认识。在初始状态t时刻：用户A只认识用户B，用户B只认识用户C，用户C只认识用户D；进入下一个时刻即t+1时刻，就可能因为在t时刻用户A认识用户B，用户B把用户C介绍给用户A，导致用户A认识用户C，即A和C两个节点之间产生连线；在t+2 时刻，可能因为t时刻用户C与用户D认识和t+1 时刻用户A认识了用户C，导致用户A认识了用户D，即A和D两个节点之间产生连线。本文在进行链路预测时提取特征的部分手段就与上述举例方法类似，即通过学习不同时刻的链路演化信息对未来时刻节点之间的链路信息进行预测。目前大多数网络表示学习算法都能有效学习静态网络［3］中节点的向量表示，然而现实世界的网络大部分都是动态的，网络中的节点和边会随着时间的推移而变化。近年来网络表示学习的算法［4］在处理动态网络时，往往收效甚微，存在不能保留动态图的长时间跨度的演化信息，面对复杂的动态网络时存在预测精度较低、模型的复杂度较高等问题。

针对近年来动态网络中存在的问题，受Kipf 等［5］提出的图卷积网络（Graph Convolutional Network，GCN）和Goyal 等［6］提出的dyngraph2vecAE 模型启发，本文提出了一种以降噪自编码器（denoising AutoEncoder，dAE）［7］为框架的动态网络表示学习模型dynGAELSTM。该模型利用GCN［5］提取图的特征向量作为dAE 的编码层输入，编码层的输出进入长短期记忆（Long Short-Term Memory，LSTM）网络采集时空依赖特征，最后输入dAE 的解码层得到下一个时刻拓扑图的预测，并加入惩罚参数和真实拓扑图进行对比得到损失函数，以此来构建链路预测［2］。将dyngraph2vecAE 模型在SBM、Hep-th、AS 三个数据集上进行实验，结果表明该模型在提高链路预测的精度和降低参数复杂度上有显著效果。

本文的主要工作如下：

1）提出了一种链路预测的动态网络表示学习模型——dynGAELSTM，该模型可以学习动态图节点之间的结构信息和时空依赖特征来预测链路，同时也实现了动态网络预测图的可视化；

2）dynGAELSTM 模型的节点采样端加入了GCN 进行高阶图邻域结构特征的提取，并利用LSTM 网络来获取动态图的长时间跨度的演化信息，在面对复杂的动态图时，预测结果更加准确；

3）dynGAELSTM 模型以节点随机断开的dAE 为框架，能有效降低模型的复杂度，提高运算效率。

1 相关工作

动态网络数据在本文中表示成一系列随时间变化的静态图像，实验时也是将此类动态数据集β={G1，G2，…，Gt} 转化为静态图G=(V，E)进行输入，其中：V代表节点的集合，E代表边的集合。

近年来的动态网络表示学习模型主要是通过施加一个时间正则化来增强相邻动态网络镜像中节点表示的平滑性。比如，2018 年Goyal 等［6］提出了使用自编码器（AutoEncoder，AE）将输入数据映射到高度非线性空间来捕捉当前时刻网络连通性的dynGEM［8］模型，并通过PropSize［8］来动态扩展模型；虽然该模型能学习到动态网络的演化依赖信息和网络的结构信息，但只用了前一个时间的网络信息进行预测，不能保留动态图的长时间跨度的演化信息。2018 年Zhou 等［9］提出的DynamicTriad 模型假设动态图的时空演化持续时间很短，仅有两个时间步长，模型采用的时间节点表示仅限于一阶邻近度的建模，忽略了高阶图邻域的结构。2019 年，Goyal 等［6］提出的dyngraph2vecRNN 模型如图2 所示。该模型利用自编码器（AE）结合循环神经网络（Rerrent Neural Network，RNN）学习复杂网络的动态信息，可以有效提取有权图的长时间跨度演化信息；但dyngraph2vecRNN 模型的高阶图邻域结构特征提取不完善，且与其他基准模型相比复杂度较高。此外，Luo等［10］提出的OptimalSVD 模型和Taheri 等［11］提出的RerunSVD模型都基于邻接矩阵的奇异值分解表示图中的各个节点，但获取高阶图邻域结构特征的能力都较差。

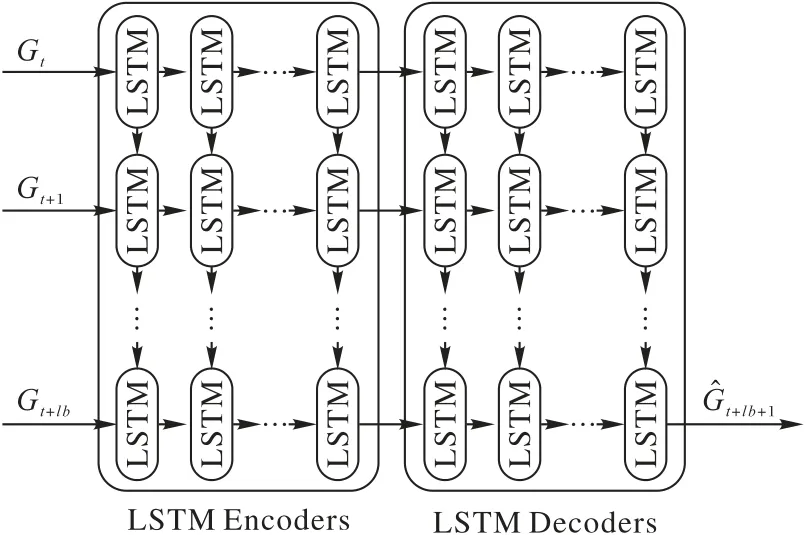
图2 dyngraph2vecRNN模型结构Fig.2 Structure of dyngraph2vecRNN model

上述近年来动态网络表示学习模型的不足之处总结如下：1）不能保留动态图的长时间跨度的演化信息；2）忽略了高阶图邻域的结构，在面对复杂的动态网络时预测精度较低；3）动态网络模型的复杂度较高。本文针对上述问题给出了相应的改进方法，提出了dynGAELSTM模型。

本文dynGAELSTM 模型的链路预测主要从动态图节点之间的特征和时空依赖特征这两方面着手。该模型受Kipf 等［5］改进的K阶多项式代替传统卷积神经网络（Convolutional Neural Network，CNN）上的卷积核的启发，并结合Bengio 等［12］提出的基于图的标签传播算法，以此抽取动态图中心节点k步范围内节点的局部结构特征；时空依赖特征的提取以Sathasivam 等［13］提出的RNN 为基础，通过历史信息的保留和输入信息来处理和预测序列数据。下面具体介绍dynGAELSTM模型的三个基本构成组件。

1.1 降噪自编码器

dynGAELSTM 模型采用了降噪自编码器（dAE）的框架，通过重建网络与输入网络进行对比，反向传播更新参数优化模型。自编码器（AE）是在2006 年由Hinton 等［14］提出的一种无监督神经网络模型，dAE 在在自编码器的隐藏层上设置了一个断开率，获得输入图的低维特征。dAE 的结构如图3所示。

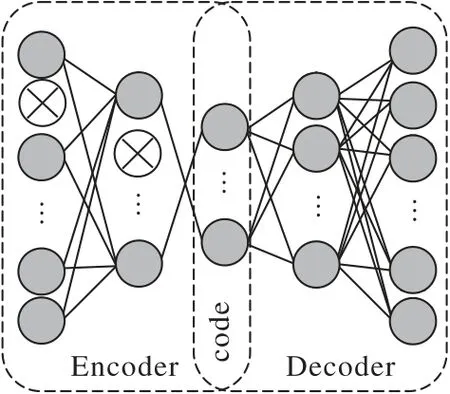
图3 降噪自编码器结构Fig.3 Structure of dAE

dAE 由编码器和解码器两个部分组成：编码器就是将输入层映射到隐藏层，并在映射过程中的节点链接之间设置一个断开率，防止干扰因素过多，避免过拟合现象；解码器则是将隐藏层的特征信息重建至输出层，和输入数据进行对比，使用梯度下降算法优化模型。此模型的组件利用其编码层的随机断开率降低模型复杂度。

1.2 图卷积网络

dynGAELSTM 模型编码器的前端加入了图卷积网络（GCN），相应的图卷积框架如图4 所示，其目的是从输入的复杂的拓扑结构中提取图的特征信息，并精简进入到dAE 的编码器的输入，其中σ(x)为图卷积层的激活函数。传统的CNN可以提取空间特征，在图像处理和语言处理等应用上效果显著，但在面对由顶点和边建立相应关系的拓扑网络时，由于每个顶点相邻点的数目不同，使用共享权值来进行卷积运算无法准确提取特征。研究图信号处理的学者基于拉普拉斯矩阵［15］的图谱分解，把拉普拉斯算子的特征函数e-iwt转变为图对应的拉普拉斯矩阵的特征向量。Kipf 等［5］在GCN［5］中加入一阶Chebyshev多项式作为卷积核，克服了传统的离散卷积在拓扑结构上无法保持平移不变性的缺点，GCN 中结合Bengio等［12］提出的基于图的标签传播算法抽取中心节点的局部结构特征，相较于传统的离散卷积神经网络，算法的复杂度从O(N2)降低到了O(N)，其中N表示节点的个数，图数据集特征提取精度提高。此模型的组件提取了高阶图邻域的结构特征信息，解决了复杂动态网络预测精度较低的问题。

图4 图卷积网络结构Fig.4 Structure of GCN

1.3 长短期记忆网络

dynGAELSTM 模型利用长短期记忆（LSTM）网络采集时空依赖特征。LSTM 网络是基于RNN［13］的一种变种，RNN 的结构如图5所示。

图5 RNN结构Fig.5 Structure of RNN

一个长度为T的序列用RNN 建模，展开之后是一个T层的前馈神经网络。其中，第t层的隐含状态ht编码了序列中前t个输入的信息，通过当前的输入xt和上一层神经网络的状态ht-1建模，隐藏状态ht和输出y的表达为：

其中：f和g为激活函数；U为输入层到隐含层的权重矩阵；U1为隐藏层到输出层的权重矩阵；W为隐含层从上一时刻到下一个时刻的状态转移的权重矩阵。

由于RNN 存在梯度弥散和梯度爆炸问题，学习能力有限，往往达不到预期的效果，于是李卫疆等［16］在RNN 的基础上给出了如图6所示的LSTM网络框架。

图6 LSTM网络结构Fig.6 Structure of LSTM network

与传统的RNN 相比，LSTM 网络仍然是基于输入xt和隐含状态ht-1来计算ht，只不过对内部的结构进行了优化设计，加入了输入门it、遗忘门ft、和输出门ot三个门和一个内部记忆单元ct。输入门控制当前的新状态以多大程度更新到记忆单元中，遗忘门控制前一步记忆单元中的信息以多大程度被遗忘，而输出门控制记忆单元在当前输出中的程度。多个此组件组合成的LSTM 网络模块可以保留动态图的长时间跨度的演化信息。

2 dynGAELSTM模型

针对第1 章总结的近年来链路预测模型的三个不足之处，在面对复杂的动态网络时预测精度较低、高阶图邻域的特征信息提取不完善的问题时，Fu 等［17］利用GCN［8］完成静态网络的节点聚类，能较好地提取高阶图的结构特征，模型的节点聚类能力强。受此启发，本文将GCN 作为dynGAELSTM 模型的前端模型来采集动态图的特征信息。面对不能保留动态图的长时间跨度的演化信息时，由于李卫疆等［16］提出的LSTM网络可以通过上一个时刻的信息来预测下一个时刻的信息，虽然可以提取部分时空依赖度，但无法保存大跨度时间的信息，于是将多个LSTM 网络层组合成LSTM 网络模块可以接收多个时间的动态图信息，因此选择LSTM 网络模块来采集动态图长时间跨度的演化信息。面对动态网络模型复杂度较高的问题时，利用dAE的编码层的随机断开率，能减少模型的节点参数，降低模型复杂度。

下面将详细阐述dynGAELSTM 模型结构和损失函数的定义。输入该模型的三个数据集都是动态图的数据集，将其划分为不同时刻的有权图G=(V，E)，其中：V代表节点的集合；E代表边的集合，∀eij∈E(i，j=1，2，3，…)，eij表示边的权重。

dynGAELSTM 模型通过学习输入的t+lb时刻之前的网络演化信息，根据第t个时刻至第t+lb时刻的输入图去预测t+lb+1 时刻的输出图。该模型以dAE 为框架，前端加入了GCN 来提炼动态图节点之间的高阶相似特征，将获得的拓扑图的节点向量作为dAE 的输入向量，使用随机断开的特性进一步获得相应的低维向量表示，将第t至第t+lb个时刻获得的低维向量输入LSTM 网络中获取其相应的低维时空依赖特征向量，并将低维向量输入解码器进行解码，重构预测图，并引入惩罚参数将预测图与真实图对比构建损失函数，以随机梯度下降的方法不断优化模型。本文dynGAELSTM 模型的结构如图7所示。

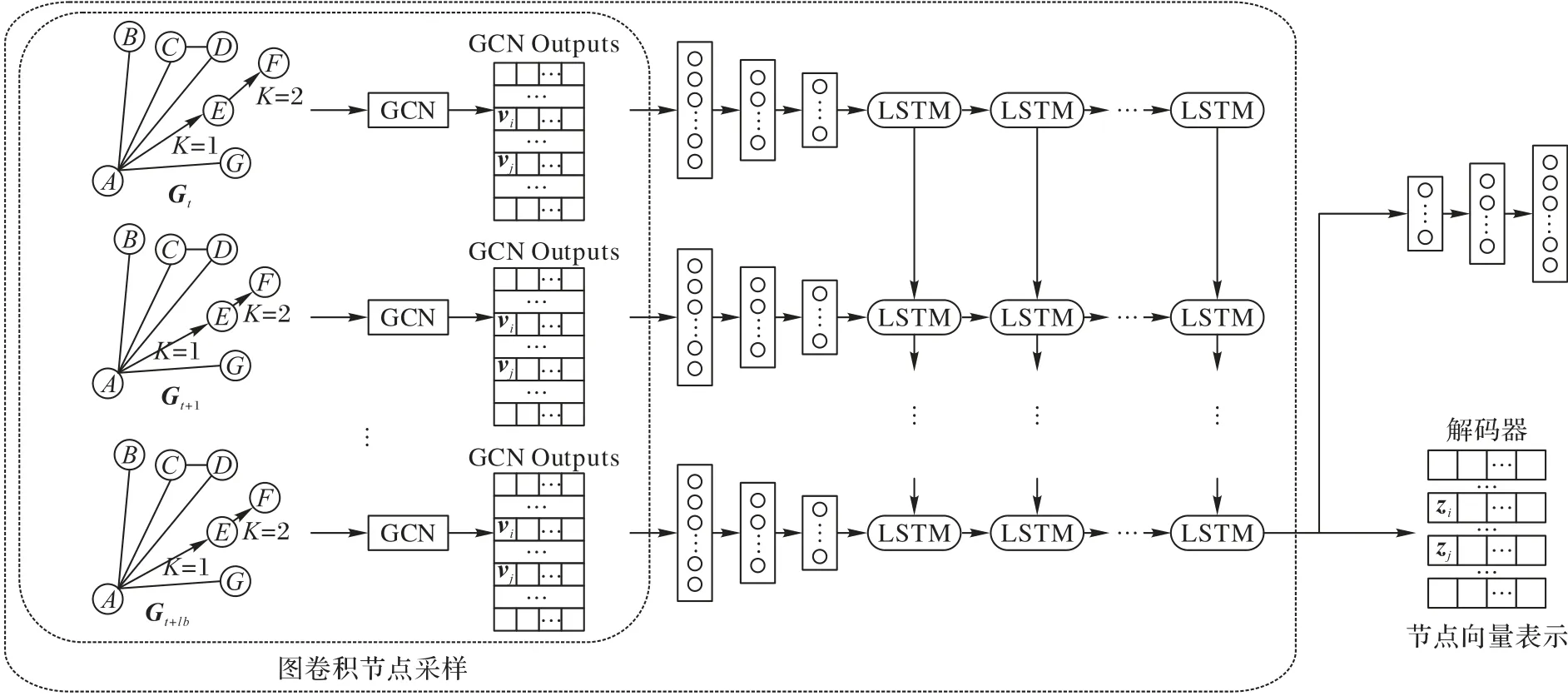
图7 dynGAELSTM模型结构Fig.7 Structure of dynGAELSTM model

GCN 层的输出进入dAE 后，输入进LSTM 网络层。LSTM网络是在RNN 中加入输入门it、遗忘门ft、和输出门ot三个门和一个内部记忆单元ct。三个门的记忆单元及节点v在t时刻的第一层LSTM网络层的定义式为：

dAE 的解码器层提取LSTM 网络层输出的时空依赖特征的有效信息，重建动态输入的网络，即为预测的t+lb+1 时刻的图。

上述为模型的GCN 层和LSTM 网络层的输出，以此为基准构建模型的损失函数。引入惩罚参数γ对图在t+lb+1 时刻不正确的重构就进行纠正，利用均方误差（Mean Square Error，MSE）的概念，将得到的预测结果与实际结果建立损失函数为：

3 实验与分析

本章将描述所使用的数据集并阐述比较基准模型的基本原理和参数设置；此外，为实验结果设置评价指标。所有实验的环境配置均在64位Ubuntu16.04.1LTS系统上进行，该系统使用型号为intel Core i7-9700KF 的CPU，具有8 个CPU 内核，主频为3.60 GHz；显卡型号为GeForce RTX 2080Ti，显存容量为11 GB。

3.1 实验数据集

本文采用了一个模拟数据集SBM（Stochastic Block Model）［6］和两个真实数据集（Hep-th［19］和AutonomousSystems（AS）［20］）对dynGAELSTM 模型进行实验，这三个数据集为Goyal 等［6］在测试dyngraph2vecAERNN 模型链路预测能力时使用的三个公共数据集，能有效评估该模型链路预测的综合能力。这三个数据集中的节点数量均不随时间的变化增加或减少，随时间改变的只有现有时间节点之间的链接关系。现将SBM、Hep-th和AS三个数据集的信息汇总于表1。

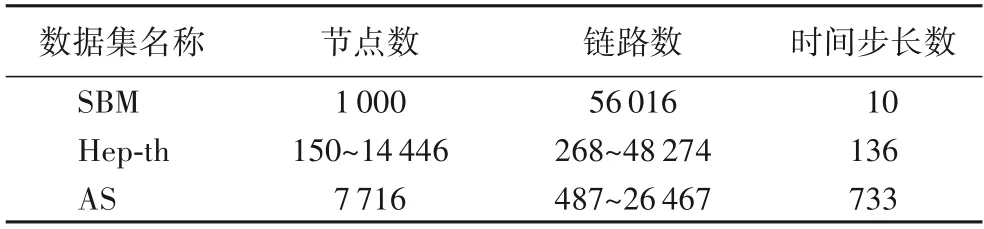
表1 数据集汇总Tab.1 Summary of datasets

SBM：该模拟数据集用Wang 等提出的随机模型，该模型可生成相应的SBM 数据集，拥有两个社区，每个社区包含500个节点，最多可以生成56 016 条链路，经历每个时间步长时，其社区间的移动概率为0.01，社区内的移动概率为0.1，该数据集随时间的不断推移，节点由一个社区逐步迁移到另一个社区，每个时间步长平均都有10至20个节点进行迁移。

Hep-th：该真实数据集是第一个用来测试动态网络模型综合能力的数据集，描述了高能物理理论会议上各作者之间合作关系的复杂网络。原始数据集包含1993 年1 月至2003年4 月期间在高能物理理论会议上的作者合作关系，每次统计其时间步长为一个月。模型实验选用该数据集从2000年4月以后的有权图。

AS：该真实数据集是基于边界网关协议（Border Gateway Protocol）日志中“与谁通话”的通信网络。数据集包含从1997年11月8日到2000年1月2日的733个实例，其时间步长为一个月。对数据集进行整理，使用该数据集的一个子集，包含最新的100个快照，共4 154个节点进行训练与测试。

3.2 基准模型

本节具体介绍与dynGAELSTM 模型做对比的其他6 种基准模型的参数设置，如表2。这6个模型主要使用的模型原理及在动态网络链路预测应用中存在的不足已经在相关工作进行了介绍。

表2 模型参数设置Tab.2 Model parameter setting

3.3 评价标准

本文中引入前k个节点的精确率［21］（Precision@k，P@k）和平均精确率均值（mean Average Precision，mAP）两个指标评估dynGAELSTM 模型在链路预测的综合性能，P@k测试模型的最高预测性能，mAP 反映模型的综合性性能。将预测为正类实际也为正类的个数记为TP（True Positive）；将预测为负类实际为正类的个数记为FP（False Positive）；将预测为正类实际为负类的个数记为TN（True Negative），在此基础上给出精确率Pr（precision）和召回率Re（recall）的定义式为：

其中：Y为链路集合。精确率反映链路预测的正确比例，召回率反映能预测出来的比例，并以节点数量进行分批实验，记为P@k，直观反映网络重构的精确率。在精确率的基础上融入召回率，设置k个召回率的阈值列表，并实验出相应的精确率，以横轴为召回率，纵轴为精确率，绘制P-R 曲线。由此平均精确率（Average Precision，AP）和mAP［22］的定义式为：

其中：SPR为在不同的召回率阈值上精确率与召回率构成的图形的面积；APi表示第i个召回率阈值的平均精确率。

3.4 节点社区预测可视化

SBM数据集由两个社区组成，在两个社区中共选取320个节点，使用OptimalSVD［10］、dynGEM［8］、dyngraph2vecAERNN［6］、dynGAELSTM 四个模型（为方便表示在图8 中分别简称为OSVD、dGEM、dAER和本文模型）通过学习前t-1个时刻的动态图进行训练，将训练好的四个模型预测t、t+1、t+2和t+3这4个时刻的预测图并在二维平面上表示出来，与真实时刻的拓扑图8（a）进行对比，结果如图8（b）～（e）所示。由于点数过多，使用不同颜色标记动态图中的10个节点，直观比较这10个节点的分布位置来比较各模型节点转移和所有节点在社区中聚类的预测性能。

图8 SBM数据集上的节点社区预测可视化Fig.8 Node community prediction visualization on SBM dataset

图8（b）、（c）为OptimalSVD 和dynGEM 两个模型在4 个不同时刻的预测图，与真实图（a）相比，可以观察出两个模型的预测图社区分类相对明显，但dynGEM 的后两张预测图社区分类的两种点互相掺杂，并且一部分红点的分布位置不在相应的社区内。图8（d）、（e）为dyngraph2vecAERNN 和dynGAELSTM 两个模型在4 个不同时刻的预测图，社区分类的区分度较高，红点的分布位置大致准确，预测精度相较于OptimalSVD 和dynGEM 两个模型的预测图有了明显的提高，但在图（d）的第一张图（t时刻）中可以观察有一个红点不在所属的社区内，图（e）的第二张图（t+1时刻）可以观察出有一个紫色节点在黄色节点所属的社区内，两相比较，可较为直观地判断dynGAELSTM 模型捕捉动态网络时空演化特征的能力略胜一筹。由于可视化中只取了一部分节点可视化出来做比较差异并不明显，下述实验中将采用三个不同的数据集进行实验比较。

3.5 实验结果

本节在SBM、Hep-th 和AS 三个数据集进行测试，GCN 上的第一层神经元个数设置为256，第二层设置为128；LSTM 网络的隐藏层单元个数为128；CNN 层第一层设置为128，第二层设置为64；dAE的断开率设置为0.1。

在SBM 数据集上的实验结果如图9 所示。为表示方便，后面的实验结果图中均用d2vAERNN、d2vAERNN 分别表示dyngraph2vecRNN、dyngraph2vecAERNN。由图9 可以得出除dynamicTriad 模型的链路预测效果较差外，其他模型在SBM数据集上前1 000 个节点的普遍精度都可以达到0.95 以上，说明dynGAELSTM 模型适合动态图的链路预测。由于SBM数据集的节点个数较少，数据信息的复杂情况一般，模型在提取特征时更偏向于对时空依赖特征的提取，因此可以说明dynGAELSTM 模型中的LSTM 网络模块能够有效提取动态图长时间的跨度演化信息。

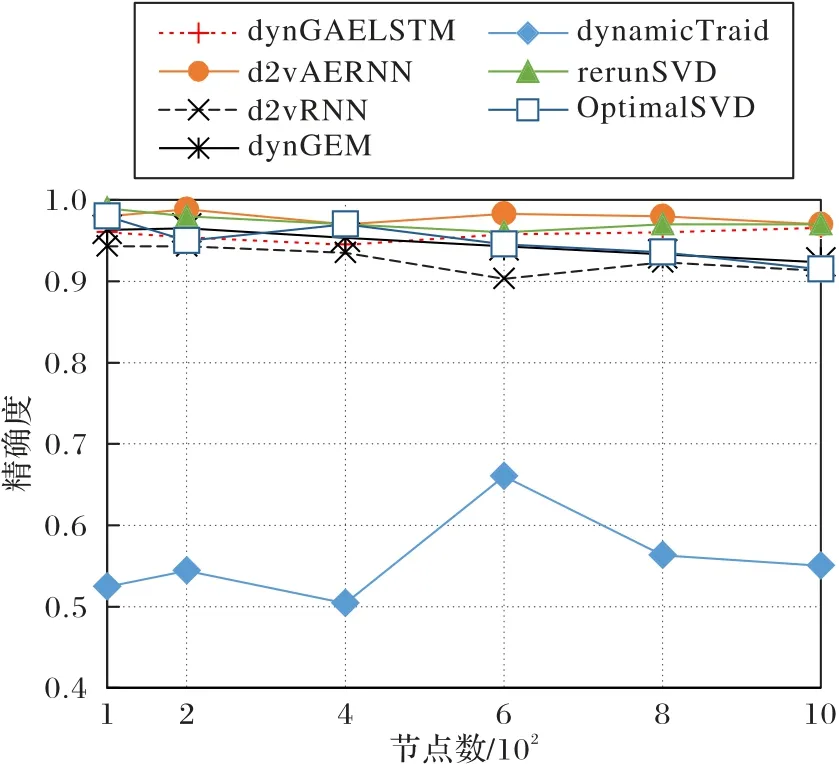
图9 SBM数据集上的P@k性能Fig.9 P@k performance on SBM dataset

在Hep-th 数据集上的实验结果如图10 所示。在Hep-th数据集上可以明显观察出dynGAELSTM 模型在前2 000 个节点的精确率在k为100，800，1 200，2 000 时都要略高于精度第二的dyngraph2vecAERNN，且前2 000 个节点的精确率都可以达到0.99 以上，dynGAELSTM 模型的链路预测能力比dyngraph2vecAERNN 模型以外的模型明显要高。Hep-th 数据集取了前2 000个节点，节点数多，链路较多，此动态图数据集的预测对时空的依赖特征和高阶图邻域结构特征的提取要求较高，dynGAELSTM 模型比其他基准模型的精度都高，足以说明模型中的LSTM 网络模块能够有效提取动态图长时间的跨度演化信息，且GCN 对高阶图邻域结构特征的信息获取能力较强。

图10 Hep-th数据集上的P@k性能Fig.10 P@k performance on Hep-th dataset

在节点和链路较多的AS 数据集上的实验结果如图11 所示。在AS 数据集上可以明显观察出dynGAELSTM 模型在前2 000个节点的精确率都高于精度第二的dyngraph2vecAERNN模型，且前2 000 个节点的精确率都可以达到0.97 以上。AS数据集相较于SBM 和Hep-th 数据集的节点数更多，链路的权重因素更复杂，模型在面对更加复杂的动态图数据集AS 时，dynGAELSTM 模型链路预测的竞争力明显强于其他基准模型，可以说明dynGAELSTM 模型的GCN 在面对关系复杂的数据集时可以高效地提取高阶图邻域结构特征信息。

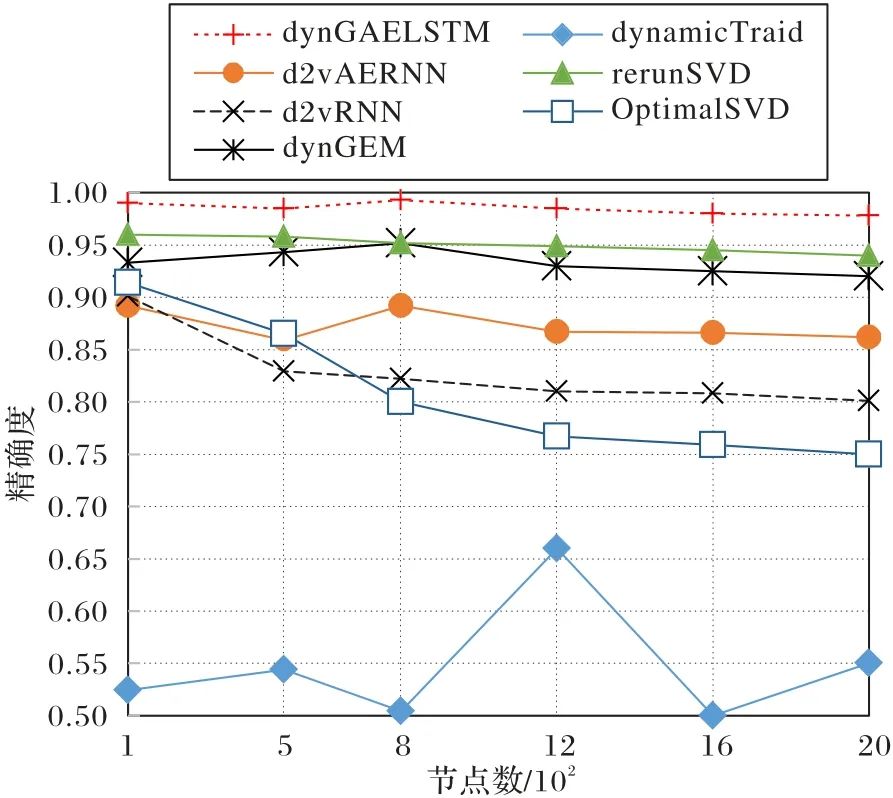
图11 AS数据集上的P@k性能Fig.11 P@k performance on AS dataset

dynGAELSTM 模型在SBM、Hep-th 和AS 三个数据集进行mAP 性能的测试，结果如表3。由表3 可得，dynGAELSTM 模型在SBM、Hep-th 两个数据集上的mAP 性能略高于dyngraph2vecAERNN 模型，提高了7.9和1.19个百分点，而且远高于其他基准模型。在复杂的AS 数据集上dynGAELSTM模型的mAP 性能比dyngraph2vecAERNN 模型高出3.13 个百分点，实验结果可以说明模型前端的GCN 提取了拓扑图的高阶特征，第t至第t+lb个时刻的LSTM 网络层获取了数据集的时空依赖特征，提升了dynGAELSTM 模型链路预测的综合性能。

表3 SBM、Hep-th和AS数据集上的mAP性能Tab.3 mAP performance on SBM，Hep-th and AS datasets

3.6 模型复杂度分析

为验证dynGAELSTM 模型的复杂度较低，将它与基准模型在复杂度上进行对比。首先与链路预测综合性能第二的dyngraph2vecAERNN 模型在模型结构上进行对比，可以看出，dyngraph2vecAERNN 模型采用了AE 的框架，编码层之间采用全连接层，节点参数并未减少；而dynGAELSTM 模型采用了dAE 的框架，节点之间设置随机断开率为0.1，在dAE 的编码层的参数量将会变为原来的0.9，后续的解码层两者都为全连接重建，参数量接近。由此可以认为：与链路预测综合性能第二的dyngraph2vecAERNN 模型相比，dynGAELSTM 模型的参数复杂程度有所下降，训练效率提高，并且预测精度更高。

复杂度的对比还借鉴了文献［23］中研究的复杂度对比方法。该方法在相同的实验环境配置下将所提出的模型作为基准，其相应的训练时间记为1×，基准模型和对比模型同时进行训练，得出对比模型的训练时间与基准训练时间的对比度，以此判断模型的时间复杂度。本次实验中，上述实验环境配置不变，在SBM 数据集取前200 个点和前300 个点进行两次实验，dynGAELSTM 模型与6 个对比模型在相同环境同时进行训练，将dynGAELSTM 模型的训练时间设为基准（记为1×），其余6个基准模型的训练时间与基准的训练时间进行对比，相应的对比度记为A×，A为相应的比值。其实验结果如表4所示。

由表4 可得出模型链路预测综合性能排名前三的模型分别是dynGAELSTM 模型、dyngraph2vecRNN 模型和dynGEM 模型，其他四个模型在三个数据集上的mAP 性能均比前三个模型下降较多，即使在表3 中dynamicTraid 模型的运行时间比dynGAELSTM 模型短，但dynGAELSTM 模型的链路预测综合性能要远高于dynamicTraid 模型，在精度相差较大的情况下不再做运行时间的对比，以精度优先。由表4 还可以看出，dynGAELSTM 模型的运行时间最短，相比预测性能第二的dyngraph2vecAERNN 模型在SBM 数据集的前200 个点上运行时间降低了0.92%，在前300 个点上的运行时间降低了1.73%。

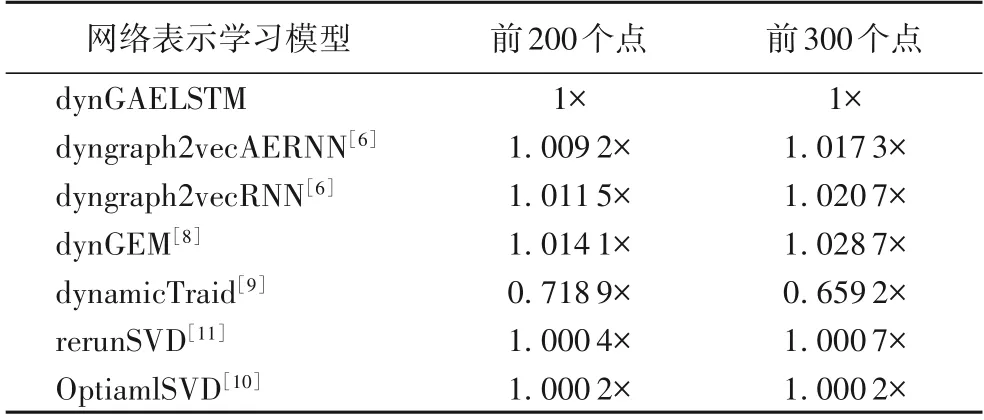
表4 网络表示学习模型在SBM数据集上的运行时间对比Tab.4 Running time comparison of network representation learning models on SBM dataset

综上所述，dynGAELSTM 模型与6 个基准模型相比，参数复杂度降低，运行效率提升，而且链路预测综合性能最高。

4 结语

本文提出了一种用于链路预测的动态网络表示学习模型dynGAELSTM。针对相关工作中总结出的链路预测模型的三个不足之处，该模型分别用了降噪自编码器（dAE）节点之间的随机断开率来降低模型的复杂度，利用图卷积网络（GCN）来提取高阶图邻域结构的特征信息，第t至第t+lb个时刻的LSTM 网络层提取动态图的长时间跨度的演化信息。在三个数据集上进行链路预测实验的结果显示，dynGAELSTM 模型在SBM、Hep-th 和AS 数据集上的精确率高，说明该模型适合动态图的链路预测，可以有效提取动态图长时间的跨度演化信息；在Hep-th 和AS 数据集上的实验结果表明，dynGAELSTM 模型在面对节点之间关系复杂的动态图时，预测精确率明显优于其他基准模型，说明它可以高效地提取网络的高阶图邻域结构特征信息。在SBM 数据集上的复杂度实验结果也表明，dynGAELSTM 模型的复杂度低于其他基准模型，运行效率更高。综上所述，dynGAELSTM 模型适合处理结构复杂和时间跨度较长的动态图的链路预测任务。

在未来的研究中，我们将针对回溯参数（LSTM 网络的层数）进行研究，探索回溯参数的设置与时空依赖特征提取之间的关联，并用复杂的数据集对模型复杂度的对比作进一步研究。