基于改进三元组网络和K近邻算法的入侵检测

王 月，江逸茗，兰巨龙

（战略支援部队信息工程大学，郑州 450001）

0 引言

信息通信系统（包括服务器、网络通信设备等）通常要处理大量敏感的用户数据，而这些数据容易受攻击。网络威胁和攻击带来了严重的安全问题由此激发了组织和个人对安全工具和系统越来越大的需求［1］。灵活、可靠、检测准确率高的实时入侵检测系统随着网络攻击技术的不断更新而成为应对安全问题的基本需求。

入侵检测系统根据网络数据来源可以分为基于网络的入侵检测系统和基于主机的入侵检测系统。基于网络的入侵检测系统通过从网络设备如交换机、路由器等收集获得的网络流量分析和检测攻击行为；基于主机的入侵检测系统可以从不同种类的日志文件、计算机资源利用率中提取系统活动事件，进而对异常进行检测。基于网络流量的入侵检测是本文的主要关注点。近年来，深度学习技术在入侵检测领域迅速发展并且出现了很多包括有监督分类方法［1-5］和无监督聚类方法［6-8］在内的相关方法。在基于深度学习的入侵检测方法中，基于深度神经网络的入侵检测系统（Deep Neural Network in Intrusion Detection System，IDS-DNN）和基于卷积神经网络与长短期记忆（Convolutional Neural Networks and Long Short Term Memory，CNN-LSTM）的检测模型是其中的典型代表。IDS-DNN的特点是具有多层隐藏层并且相邻隐藏层之间是全连接方式，使得该模型具有很强的表征能力；但IDS-DNN 的网络规模会随着输入样本的维度线性增加并且计算效率降低。在CNN-LSTM 模型中，CNN 的共享卷积核能够缩小神经网络规模并提高计算效率，LSTM 能够学习时序特征；但CNN中的池化层会丢失大量有价值的信息，而且LSTM 模型的计算复杂度较高。本文对目前的网络入侵检测方法进行调研，重点关注基于深度学习的网络入侵检测方法的研究，发现仍存在以下问题：1）大部分方法所用数据集比较过时，年代久远的KDD99 数据集被大量用于验证，因此无法反映不断更新变化的攻击特征而缺乏实用性；2）现有的基于异常的入侵检测统存在高误报率并且在较新的数据集上由于复杂的网络攻击行为表现出较低的检测准确率；3）在分类任务中，尽管数据特征很重要，但有些表示形式和相应的诱导度量可能对分类起副作用。以上述三个问题为研究动机，为进一步提升分类模型的检测准确率和计算效率，利用三元组网络模型学习高效的距离表示，并且学习对检测结果更有用的特征，进而基于距离特征进行正常和异常攻击行为的识别［9］。本文提出一种改进三元组网络（improved Ttriplet Nnetwork，imTN）结合K 近邻（K-Nearest Neighbor，KNN）算法的网络入侵检测模型imTNKNN，以提升检测准确率和计算效率，并在最近公开的入侵检测数据集CSE-CIC-IDS2018（以下简称IDS2018）进行了验证。

本文的主要工作包括：

1）将经典的深度度量学习模型三元组网络引入网络入侵检测领域并对其进行多方面改进，而且通过实验验证了三元组网络适用于入侵检测领域。

2）结合KNN 进一步提升检测准确率，将三元组模型输出的待测样本与各个正例样本的距离向量，以及待测样本与各个负例样本的距离向量作为KNN分类器的输入，由KNN分类器进一步学习得到更加准确的分类结果。

3）采用最近的公开数据集IDS2018 进行实验评估，并与多个表现良好的模型进行比较。

1 相关研究

1.1 入侵检测方法

网络入侵检测方法可以分为基于统计的检测方法、基于信息论的检测方法、基于传统机器学习的检测方法和基于深度学习的检测方法。

1.1.1 基于统计和信息论的方法

基于统计的方法大多广泛地应用于信息技术发展初期，包括混合模型和主成分分析［10］等。基于信息论的方法，主要使用信息熵、条件信息熵、信息增益、信息成本作为数据集的特征衡量指标［11］。

1.1.2 基于传统机器学习的方法

传统机器学习包括有监督分类方法和无监督聚类方法。Heller 等［12］将支持向量机（Support Vector Machine，SVM）用于网络异常检测，但假设训练集中不能存在噪声，在实际中不可行。Yang 等［13］将基于规则的方法用于采用深度分析协议的IEC 60870-5-104 数据采集与监视控制网络。基于传统机器学习的无监督聚类包括K 均值聚类和层次聚类等方法。吴剑［14］提出了一种将遗传算法和K均值聚类结合的入侵检测方法以解决入侵检测中的特征选择问题。Noorbehbahani 等［15］提出一种半监督流分类算法，使用增量聚类算法和监督方法创建初始分类模型，支持不平衡数据，并使用数量有限的带标签实例和有限的存储来实现高性能。传统机器学习入侵检测方法存在的主要问题包括：缺乏一套协商一致的输入特征以实现特定目标，例如网络安全、异常检测和流量分类等；与深度学习模型相比，传统机器学习方法的检测准确率不够高。因此在需要智能分析和高维数据学习时，传统机器学习通常不符合要求。

1.1.3 基于深度学习的方法

近年来，出现了很多基于深度学习的网络入侵检测方法，在检测性能上更具优势。Kim 等［2］采用长短期记忆（Long Short Term Memory，LSTM）模型进行网络入侵检测，可以很好地检测到攻击，但未能解决误报率高的问题。在此基础上，Zhu等［16］在LSTM 中引入注意力模型，在多分类问题上提高了准确性。Li 等［3］在NSL-KDD 公开数据集和边界网关协议（Border Gateway Protocol，BGP）路由数据集上对比了多种LSTM 模型和门控循环单元（Gated Recurrent Unit，GRU）模型的检测准确率。Vinayakumar 等［1］设计了一种深度神经网络入侵检测模型，并对网络结构和参数进行优化设计。另有一些研究提出的混合神经网络模型能取得良好检测效果，如Yuan等［17］和Saaudi等［18］将卷积神经网络与长短期记忆（CNNLSTM）模型用于内部威胁检测，对日志文本数据进行用户行为建模分析；Agarwal 等［19］同样利用CNN 和LSTM 的组合优势实现流量数据的攻击检测。但是这些方法大部分仍然使用过时的网络数据集进行验证，对当前现实世界的网络流量变化缺乏考虑。深度学习模型的计算效率远低于传统的机器学习方法，需要进一步提升深度学习模型计算效率以满足入侵检测的实时性要求。

1.2 三元组网络

深度度量学习已经广泛应用于图像识别和人脸检测等领域，利用不同对象的相似度分析来完成任务。三元组网络是由Hoffer等［9］提出的一种典型深度度量学习模型，核心思想是通过学习使相似样本之间的距离尽可能小而不相似样本之间的距离尽可能大。实验表明在多个图像数据集上三元组网络的分类准确率比CNN 等模型更突出，为进一步利用三元组网络的性能优势，很多改进算法被提出。如Ustinova 等［20］提出了基于直方图损失函数的三元组网络。在直方图损失函数中，相似样本对和不相似样本对排列组成概率分布，将相似样本对和不相似样本对的累计密度分布相乘，再进行积分得到直方图损失函数。通过直方图损失函数可以缩小相似样本和不相似样本之间的重叠。实验表明，在行人重识别数据集上基于直方图损失函数的方法拥有较好的识别率；但该方法的局限是相似性评估仍采用单一方式，即样本对的自相似性。Song等［21］认为采用传统的方法可能会使同类别相似性差异较大，并且提出了一种基于簇的相似度度量方法；但该方法需要采用大量贪婪搜索操作寻找簇中心以获得局部最优值，计算效率较低。Wang 等［22］认为现有深度度量学习模型的不足之处是普遍采用单一的相似度度量，因此提出了一种多重相似度损失函数，结合了样本对之间的自相似性、负样本对之间的相对相似性以及正样本对之间的相对相似性等多种相似度衡量方式。实验表明该方法在多个图像检索数据集上的性能优于其他方法。

不少相关研究证明了三元组网络的表现优于传统的深度学习模型，目前主要应用于图像处理领域。本文探索了如何将三元组网络用于入侵检测领域，并通过优化设计网络结构、损失函数以进一步提升入侵检测方法的检测准确率、计算效率等性能指标。

2 算法设计

深度度量学习过程中产生了相似度距离特征，可用于分类。在此首次将一种典型的名为三元组网络的深度度量模型应用于网络入侵检测，并改进了传统三元组网络以在网络入侵检测中发挥优势，而且结合KNN 分类器进一步学习得到二分类结果，实现高精度网络入侵检测。

2.1 传统三元组网络

三元组网络中，三个样本a、b和c作为输入。其中，样本a和b属于同一类别，样本c属于不同类别。假设样本a和样本b间的距离为d1，样本a和样本c间的距离为d2。学习目标是最小化同类样本之间的距离而最大化不同类样本之间的距离。

其中距离di用欧氏距离计算，公式如下：

距离特征d1和d2归一化后，距离向量中各元素和等于1，产生输出向量：

每个（a，b，c）三元组所对应的输出向量的取值范围是［0，1］。传统三元组网络架构如图1所示。

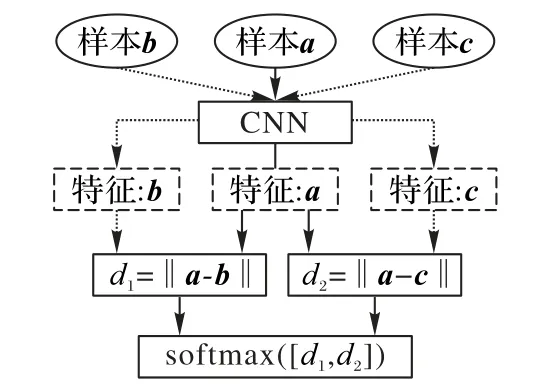
图1 三元组网络架构Fig.1 Architecture of triplet network

在2.3 节中详细描述了对传统三元组网络的改进，包括卷积层结构和参数、批量归一化（Batch Normalization，BN）层和损失函数以最大化入侵检测准确率和计算效率。

2.2 KNN

KNN 因为简单有效且容易实现而广泛应用［23］。KNN 算法的基本思想：首先，把训练样本作为欧氏空间的点存放，所有样本对应于n维空间的点，根据客观事实或专家经验，给训练数据设定分组；然后，挑选训练样本集中与待分类样本距离最近的k个样本；最后，根据这距离最近的k个样本的类别标签对待预测样本进行分类。

近邻数k是KNN 的参数，对模型训练精度起决定性作用，本文主要通过实验确定最优k值。

2.3 改进三元组网络和KNN组合模型

三元组网络预测模型输出样本间的距离向量，将待测样本与正例样本距离求和得到d1，待测样本与负例样本距离求和得到d2。理想情况下，当d1≤T，认为待测样本是正例；当d1＞T，认为待测样本是负例。用于网络入侵检测时，由于正例样本间也存在较大差异，难以确定合适的阈值T。为解决这个问题，将三元组模型输出的距离向量作为KNN 分类器的输入，由KNN分类器进一步学习得到二分类结果。

为提升KNN 的计算效率和检测精度，将得到的距离向量按照先后次序分成s组，对每组向量求平均值，将这s个平均距离向量作为KNN 的输入。imTN-KNN 模型架构如图2所示。

图2 imTN-KNN架构Fig.2 imTN-KNN architecture

适用于网络入侵检测领域的改进三元组网络模型中CNN网络结构设计如表1所示。

表1 改进三元组网络采用的CNN结构Tab.1 CNN structure employed by improved triplet network

在改进三元组网络中移除了BN层。BN层在图像处理领域主要应用于输入图像的数据分布和输出数据的分布不一致或有很大变动的情况，它在该应用领域具有良好的表现；但在网络入侵检测领域，输入与输出的数据分布一般一致，因此去掉它影响不大。相反，加入了BN层导致输入输出的数据分布发生了不必要的变化从而造成了信息损失，进而给检测准确率的提升带来了负面影响。此外，移除BN层可以减小内存消耗并提升计算效率［24］。

损失函数一般用于机器学习中预测模型的预测准确率衡量。损失函数的选择需要考虑很多问题，并且发现一个适合于大部分数据集的损失函数比较困难。

在三元组网络中，损失函数的设计对于提升模型性能指标比较关键，近年来出现了不少有关三元组损失函数的研究。Hoffer 等［9］提出了主要关注同类样本和不同类样本的相似性的经典三元组损失函数，通过训练减小同类样本的相似距离而增大不同类样本之间的相似距离。这种方法生成的大量成对样本是高度冗余的且包含很多无信息样本。后来又出现了很多其他类型的用于度量学习的损失函数，包括提升结构损失函数［25］、直方图损失函数［20］、层次三元组损失函数［26］等。经典三元组损失函数在批量训练大小较小时很难利用所有的样本对之间的关系，为了应对这个问题，研究者提出了提升结构损失函数；但结构损失函数仅随机采样相等数量的正例样本对和负例样本对，依然损失了大量信息。直方图损失函数将同类样本对和不同类样本对进行排列组成概率分布，通过概率分布使得不同类样本的相似性远小于同类样本的相似性。直方图损失函数的优点是不需要额外参数，并且不需要困难样本挖掘，但缺点是计算复杂度较高。在层次三元组损失函数中，建立了所有类的层次树，样本对的选择依据一个动态的边界阈值。层次三元组损失函数虽然提升了检测准确率等性能但实现比较复杂。Wang 等［22］对度量学习中的损失函数进行了全面深入分析，研究了这些损失函数的共性，发现关键的影响因素是数据样本的包含自相似度和相对相似度在内的多种相似度，其中相对相似度主要取决于其他样本对。但大多数现有方法仅探索了自相似度和相对相似度其中的一个因素，于是提出了多重相似性损失函数。本文最终采用Wang等［22］提出的多重相似性损失函数，它从多个角度对相似性进行衡量，克服了以往对相似度衡量的片面性。具体地，多重相似性损失函数能够从自相似性、负例相对相似性和正例相对相似性三方面评估损失值，该损失函数表达式为：

其中：m为训练样本数，Sij表示两个样本i和j的相似度。在改进三元组网络模型中采用多重相似函数获得了两方面的收益：一是通过对嵌入大小embedding_size进行调参的方式明显提升实验部分的检测准确率；二是提升了模型训练的收敛速度，训练过程中经过第一次迭代就获得了最好的检测准确率，大幅节省了训练时间、提升了计算效率。

此外，使用高效的自适应学习率优化器Adam［27］，为不同的参数设计独立的自适应性学习率。学习率值设定为0.000 1，β1=0.9，β2=0.999。

2.4 imTN-KNN算法流程

算法主要包括数据预处理、模型训练和模型测试等主要步骤，模型训练和模型测试阶段通过不断迭代来得到最优的网络参数（如图3所示）。

图3 imTN-KNN流程Fig.3 Flowchart of imTN-KNN

公开基准数据集IDS2018 包含了提取的80 多个特征数据，这些数据需要预处理，包含两个操作：一是将无穷大或者空值异常数据进行修正和补齐；二是进行归一化处理。为保证数据尽量不损失信息并且确保数据均映射到［0，1］区间内，采用最小值-最大值函数（Min-Max）进行归一化以实现对原始数据的等比缩放。函数Min-Max定义为：

经过预处理的数据集被分成训练数据集和测试数据集分别用于训练和测试阶段。以上所有样本子集都从总样本集中随机选取，不作人为筛选。

3 实验评估

实验硬件环境包括：Intel Xeon（Cascade Lake）Platinum 82692.5 GHz/3.2 GHz 的4 核心中央处理单元（Central Processing Unit，CPU），8 GB 内存。在基准数据集IDS2018 上进行实验评估，与现有性能良好的深度学习算法进行对比，验证imTN-KNN的有效性。此外，imTN-KNN还与浅层学习方法主成分分析（Principal Component Analysis，PCA）和KNN 相结合的PCA+KNN、SVM［28］、PCA+SVM［28］和朴素贝叶斯（Naive Bayes，NB）［29］进行了对比，验证了改进三元组网络模型进行特征提取的高效性。

3.1 数据集

IDS2018 是一个包含大量网络流量和系统日志的数据集，通过10 天的数据采集获得，每天的数据形成一个数据子集，总大小超过400 GB。该数据集包括7 种攻击类型和16 种子类型攻击的有场景标记的数据，包括暴力破解、拒绝服务（Denial of Service，DoS）攻击、监视网络攻击和渗透攻击等。通过特征生成工具CICFlowMeter-V3［30］分析IDS2018 数据集，生成约80 种特征数据，表征了网络流量和数据包的活动行为。在相关研究基础上，本文选取两个检测精度比较高的数据子集（分别简写为Sub_DS1 和Sub_DS2）和一个检测精度比较低的数据子集（简写为Sub_DS3）作为实验的测试集。这三个数据子集在已有模型中的检测准确率差异较大，对验证模型具有代表意义，数据子集的说明如表2所示。

表2 IDS2018三个数据子集概要Tab.2 Summary of three data subsets of IDS2018

3.2 对比算法

基于深度学习的入侵检测算法近年来得到广泛研究，相关研究表明：IDS-DNN 和CNN-LSTM 在性能指标上达到了良好的效果，前者能够自动提取高级特征，后者在捕捉时间和空间特征上具有优势。基于上述原因，本文选择IDS-DNN 和CNN-LSTM两种深度学习模型作为对比模型。

IDS-DNN 结构包含6 个Dense 层和1 个激活层。为防止过拟合，Dense 层之间加入Dropout 层。每个Dense 层的维数如表3 所示。激活层采用Sigmoid 函数，Dense 层激活函数采用线性整流单元（Rectified Linear Unit，ReLU）函数。损失函数为二元交叉熵函数，优化函数为Adam［27］。

表3 IDS-DNN结构Tab.3 Structure of IDS-DNN

CNN-LSTM［19］混合网络结构如表4所示，其损失函数为稀疏分类交叉熵函数，优化函数为Adam。

表4 CNN-LSTM结构Tab.4 Structure of CNN-LSTM

3.3 衡量指标

采用全局准确率Acc（Accuracy）、正例准确率AccP（Accuracy of Positives）、负例准确率AccN（Accuracy of Negtives）、假正率FPR（False Positive Rate）、真正率TPR（True Positive Rate）和模型训练时间Training_Time等指标对模型进行对比分析［1］。

本文将训练时间用作易于衡量的计算效率的指标。减少模型的训练时间不是提高计算效率的唯一目标，但训练时间通常与其他计算效率指标呈正相关关系，例如模型测试时间或在线响应时间。He 等［31］详细分析了CNN 模型的在训练阶段的时间复杂度。该文献中涉及到的相同的理论公式同样适用于分析训练时间和测试时间。基于以上考虑，本文采用训练时间作为检测计算效率的衡量指标。

3.4 实验对比分析

首先，与检测准确率较高的浅层机器学习方法SVM、PCA-SVM 以及NB 进行对比，imTN-KNN 只采用一层包含32个单元的卷积层就能够获得最高准确率，而且对比时已将SVM［28］、PCA-SVM［28］、NB［29］方法中的参数调整到最优值。在这种情形下，尽管因为深度学习模型本身的复杂性导致imTN-KNN 的归一化训练时间大于其他浅层机器学习方法，但在调整检测计算效率与检测准确率性能的平衡方面，imTNKNN 具有更强的自由度（如表5所示）。关注检测准确率的网络入侵检测应用场合更适合采用imTN-KNN 等深度学习模型。此外，对于某些动态复杂场景可以将imTN-KNN 深度学习模型和PCA+SVM等浅层学习模型结合起来使用。

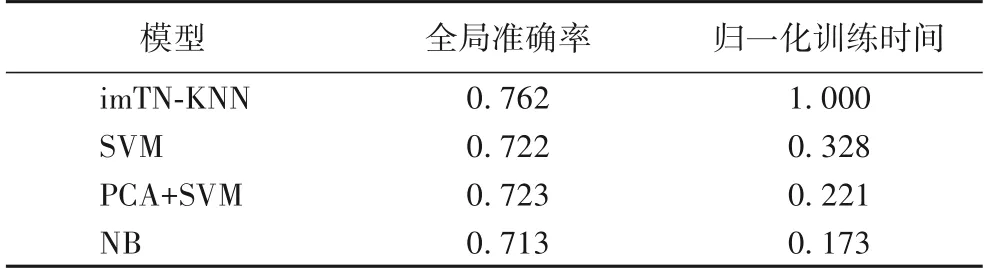
表5 imTN-KNN与浅层机器学习模型性能对比Tab.5 Performance comparison between imTN-KNN and shallow machine learning models

图4 呈现了imTN-KNN、IDS-DNN、CNN-LSTM 和PCAKNN 在数据子集上的Acc对比，图5 和图6 分别为不同数据集上四个算法的AccP和AccN分析。可以看出，在Sub_DS1、Sub_DS2和Sub_DS3三个数据子集上，imTN-KNN 的性能都优于其他方法。其中在Sub_DS3 数据子集上，相比IDS-DNN、CNN-LSTM 和PCA-KNN，imTN-KNN 的Acc分别提升2.76%、4.68%和6.53%。值得注意，在Sub_DS3 数据子集上所有模型的表现都不够理想，说明渗透攻击和正常流量的区分度不高，现有模型对这种攻击类型的检测率依然偏低。

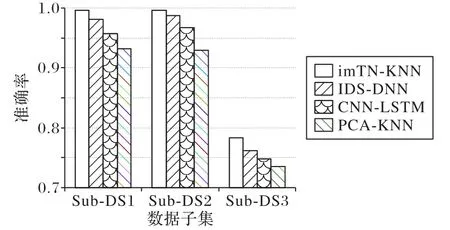
图4 识别准确率对比图Fig.4 Comparison of Acc

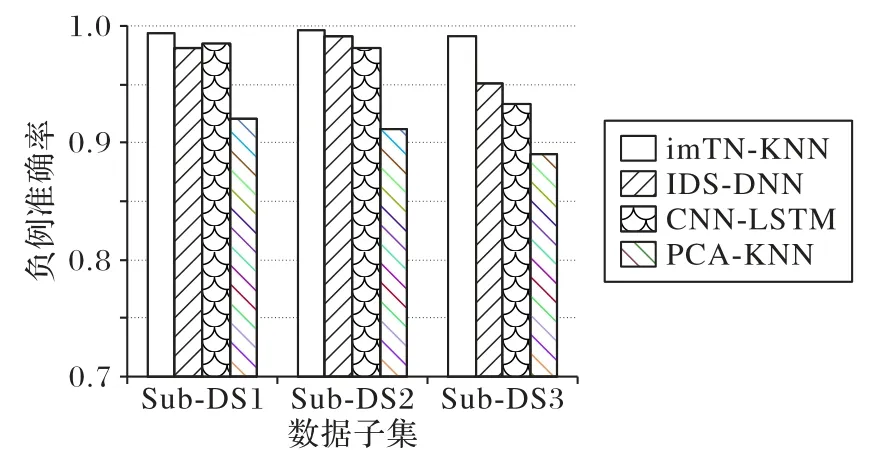
图5 负例识别准确率对比Fig.5 Comparison of AccN

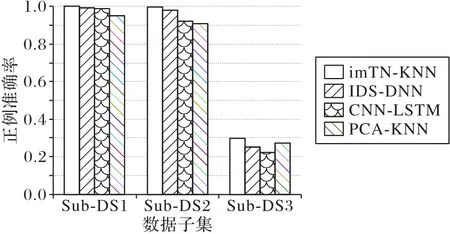
图6 正例识别准确率对比Fig.6 Comparison of AccP

在数据集Sub_DS3上，检测模型的Acc随训练样本个数的变化如图7所示。可以看出，imTN-KNN和IDS-DNN在小样本训练时比CNN-LSTM 更具优势，但随着训练样本数增多，imTN-KNN 和IDS-DNN 的Acc逐渐缓慢降低，而CNN-LSTM 的Acc开始缓慢上升至逐渐超过DNN 并接近imTN-KNN。训练样本数在从2 000 到140 000 变化的过程中，imTN-KNN 的Acc总是高于其余三个方法，尤其在训练样本数为2 000时，imTNKNN 的Acc明显高于IDS-DN、CNN-LSTM 和PCA-KNN，说明imTN-KNN 更适合小样本场景，这与在图像检测领域的性能表现一致。

图7 训练样本数对检测准确率的影响Fig.7 Influence of training sample number on detection accuracy

图8展示了其他参数保持不变的情况下，KNN中参数k值在10 到170 变换过程中，imTN-KNN 和PCA-KNN 检测准确率的变化。从图中可以看出两个方法的检测准确率都随着k值的变大先变大再变小并且变化较大，最优k值都是50。虽然imTN-KNN 的检测准确率受k值的影响更大，但imTN-KNN 的检测准确率总是明显高于PCA-KNN。

图8 KNN中参数k对检测准确率的影响Fig.8 Influence of parameter k in KNN on Acc

在数据子集Sub_DS3 上，四个方法的受试者工作特征（Receiver Operating Characteristic，ROC）曲线由图9 所示，可以看出imTN-KNN 的总是优于其余方法。相比IDS-DNN、CNN-LSTM 和PCA-KNN，imTN-KNN 的ROC 曲线下面的面积（Area Under ROC Curve，AUC）分别提升了6.53%、7.03%、8.10%。

图9 ROC对比Fig.9 Comparison of ROCs

图10 呈现了在训练迭代次数e从1 到10 变化过程中，imTN-KNN、IDS-DNN 和CNN-LSTM 三个模型Acc的变化。这三个模型取得最优Acc值时，对应e的值分别为1、7、9，说明在模型训练时imTN-KNN 的收敛速度远快于IDS-DNN 和CNNLSTM；这三个模型在达到最优Acc时所用的归一化训练时间分别为0.256 9，0.843 9 和1。imTN-KNN 的归一化训练时间远小于其余两个模型，相较于IDS-DNN 和CNN-LSTM，imTNKNN缩短训练时间分别高达69.56%和74.31%。

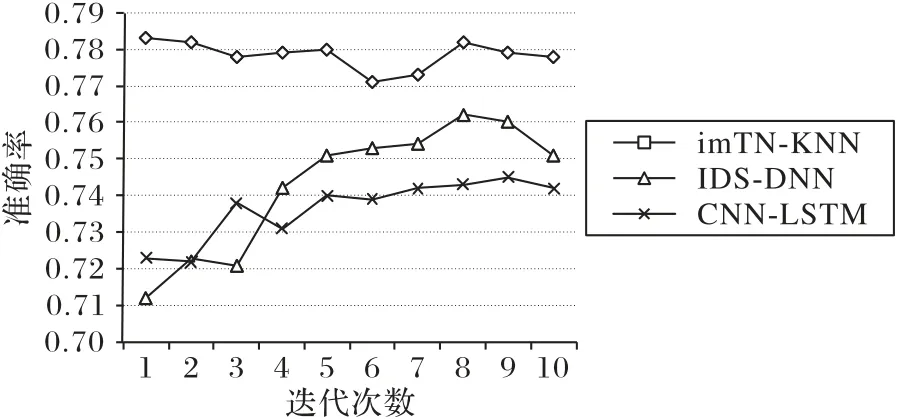
图10 迭代次数对模型准确率的影响Fig.10 Influence of iteration number on accuracy

4 结语

针对用深度学习解决网络入侵检测问题时计算效率普遍低下的问题，本文借鉴深度度量学习思想，以距离特征作为分类标准，提出了imTN-KNN 模型。从CNN 结构和参数角度改进了传统三元组网络，用Dropout 层和Sigmoid 激活函数层替换了BN 层。此外，利用高效的KNN 分类算法学习距离特征，解决了依据特定阈值进行简单分类导致检测精度不高的问题。在公开数据集IDS2018 上的实验结果表明，与其他算法相比，imTN-KNN 能更好地兼顾检测准确率和计算效率。在后续研究中，为提高对渗透攻击的识别率，需要在保证检测率的计算效率的同时尽可能多地学习原始流量中包含的信息以进一步提高入侵检测模型的检测准确率和检测计算效率等多种性能。