集中荷载和均布荷载下T形简支梁不同截面的剪力滞效应
2021-07-30赵明岩董毓利雒家琪
赵明岩, 董毓利, 雒家琪
(华侨大学 土木工程学院, 福建 厦门 361021)
混凝土T形薄壁梁具有良好的抗弯性能,这种结构形式广泛应用于城市高架道路、立交桥等,且更倾向于应用大悬臂结构,但其受力特性较为复杂,与传统矩形截面等相比,T形截面的剪力滞效应尤为突出[1-2],其中,温度、梁高、腹板厚度等参数的变化都会影响剪力滞效应[3-5],而同一截面剪力滞效应沿翼缘分布是不均匀的[6].剪切变形对梁挠度的影响不仅反映在剪力自身引起挠度,即竖向相邻截面滑动,还反映在剪切变形对翘曲函数的影响,进而导致附加挠度的增加[7].在荷载作用下,T 形简支梁翼板内靠近支座位置区域存在显著的负剪力滞现象[8].因此,应用初等梁理论,进行混凝土抗弯性能试验研究时,探究翼板剪力滞效应分布规律是关键.
国内有很多针对剪力滞效应研究的理论方法,罗旗帜[9]利用有机玻璃箱梁模型开展试验,研究连续箱梁和简支箱梁的剪力滞效应,验证了基于能量变分法原理研究剪力滞效应的准确性.程海根等[10]采用级数近似解的方法,计算组合箱梁剪力滞效应,且得到较满意的结果,表明该方法对箱梁进行简化分析是足够的.本文采用有机玻璃T形简支梁代替混凝土,从试验数据出发,探究剪力滞沿翼缘的分布规律[11-12],重点研究在集中荷载和均布荷载作用下,T形简支梁的剪力滞系数沿翼缘长度方向的传递规律,将试验和理论结果进行对比分析.
1 试验概况
1.1 试验模型
为研究集中荷载和均布荷载作用下有机玻璃T形简支梁的剪力滞效应,依据JTG D60-2015《公路桥涵设计通用规范》[13],参考杨燕飞[14]研究的悬臂T梁交接处的剪应力传递模型设计试验模型.T形简支梁长度(L)为900 mm,腹板高度为72 mm,腹板宽度为10 mm,翼板宽度为200 mm,翼板厚度为8 mm,两端设有厚度为25 mm的隔板,以增强简支梁的稳定性.T形简支梁模型的设计,如图1所示.

(a) 模型平面图 (b) 截面尺寸及应变片布置
选择有机玻璃作为模型材料,因为有机玻璃与应变片连接更紧密,应变片不容易损坏,且有机玻璃与混凝土力学性能相似,有良好的弹性性能,可以更好地模拟桥梁的力学性能,易于制作同系数三维模型缩尺,对实际桥梁尺寸进行同系数缩放,可以更好地贴合实际.经试验测得材料的弹性模量E=2 425 MPa,泊松比μ=0.436 5[15].
1.2 试验装置及加载方案
由于T形简支梁在放置时不具稳定性,故在支座两端设置厚度为25 mm的隔板以增加稳定性,在保证构件不发生开裂的情况下,使构件保持在弹性范围内.为了研究有机玻璃T形简支梁模型的剪力滞效应,取跨中7个控制截面(A-A,B-B,C-C,D-D,E-E,F-F,G-G)作为研究对象,每个控制截面上、下共布置25个应变片(图1(b)).
简支梁集中荷载研究采用分配梁对称加载,加力螺栓下方连接压力传感器和电子读数,控制加载力大小,分4级加载,每级100 N,加载点布置在简支梁三分点处.均布荷载采用砝码加载,每个砝码质量为3 kg,分4级加载,每级满布5个砝码.集中加载和均布加载的力作用点均为腹板对应的翼板位置,每级加载完毕后,采用DH3816型静态应变采集仪记录15 min内的应变变化,收集应变测量数据.计算简图和加载装置,如图2所示.图2中:P为集中荷载;q为均布荷载.

(a) 计算简图
2 试验结果及分析
2.1 试验结果
为了更好地研究剪力滞传递机理,工程中采用剪力滞系数(λ)表示剪力滞效应的大小,其计算式为

(1)

T形截面中性轴在距底端63.6 mm处,对Y轴的惯性矩IY=1 114 056 mm4,初等梁理论应力的计算式为
(2)
式(2)中:M为弯矩;y为计算截面至中性轴距离.
根据结构力学求解器计算所得集中荷载(P)和均布荷载(q)作用的弯矩,得到理论正应力结果,如表1所示.由于A-A截面位于边缘支座处,数据稳定性较差,故不作为代表性数据.

表1 理论正应力结果
考虑到T形简支梁受力基本处于弹性范围内,采取相同试验重复进行,利用截面对称性,取平均值作为最终试验结果,研究成果主要包括不同截面翼板的应变分布和剪力滞系数分布.
在不同荷载作用下,测得有机玻璃T形简支梁不同截面的应变分布.取拉应变为正,压应变为负.为了减少试验误差,采取相同试验进行多次,取各组数据的应变平均值.
由于截面G-G位于支座位置处,在集中荷载和均布荷载作用下,截面不承受弯矩,正应力为0,只承受剪力.将截面G-G翼板上表面应变(ε)作为研究对象,在不同荷载作用下,截面G-G的应变分布,如图3(a),(b)所示.由图3(a),(b)可知:施加第1级荷载后,截面G-G的应变变化均表现为翼板腹板处最大,向两侧逐渐变小,且翼板两侧出现了压应变.集中荷载和均布荷载作用位置均为翼板腹板处,根据圣维南原理,翼板腹板处一定范围内会出现拉应变且应变较大.在支座位置,支座反力通过隔板传递给翼板,使腹板处翼板出现拉应变,忽略支反力作用,腹板处翼板应为压应变,即将图3(a),(b)的应变平移至0以下,变为压应变,但应变的变化趋势不变,此时,腹板处翼板应变绝对值小于相邻截面应变值,为负剪力滞效应.
截面G-G翼板变形示意图,如图3(c)所示.由图3(c)可知:在支座处,由于支座反力作用,翼板出现了虚线所示变形,翼板腹板受拉,边缘受压,两部分变形量不一致.

(a) 集中荷载作用 (b) 均布荷载作用
为方便讲述,取支座附近隔离体,分析截面的受力状态.T形简支梁受支座集中力作用,翼板产生变形的平面图及受力分析,如图4所示.
由图4可知:隔离体1为靠近支座一侧,翼板两侧为压应变,中间为拉应变,截面A-A移动到虚线所示位置;由于结构具有连续性,截面A-A和截面B-B为同一截面,满足变形协调条件,截面B-B对截面A-A有力的约束,应变方向不同导致约束方向不同(图4(b));翼板腹板处受压,压应变向两侧减小,逐渐变为拉应变,边缘处与翼板腹板处位移差最大,拉应力最大.故在T形简支梁翼板出现边缘应力大于翼板腹板处应力的负剪力滞效应,随荷载的增加,负剪力滞效应逐渐增强.

(a) 翼板变形图 (b) 翼板受力分析
由于加载点位置具有对称性,故只分析截面F-F,E-E,D-D.截面F-F距左侧支座90 mm(L/10).集中荷载作用下,截面F-F翼板上表面应变及剪力滞系数,如图5所示.因应变数值的正负号仅代表方向,故根据绝对值判断应变大小.由图5可知:第1级荷载(100 N)加载时,翼板腹板处应变大于相邻两测点应变,为正剪力滞效应;随着荷载的增加,腹板处应变与相邻测点应变的差值逐渐增大,截面F-F在各级荷载作用下,翼板腹板处及相邻两测点的剪力滞系数均小于1,且变化趋势基本相同,翼板腹板部分范围内的剪力滞系数小于1,向两侧逐渐增大至大于1.

(a) 上表面应变 (b) 剪力滞系数
均布荷载作用下,截面F-F翼板上表面应变及剪力滞系数,如图6所示.由图6可知:第1级荷载(166.7 N·m-1)加载后,翼板腹板处应变大于相邻测点应变,为正剪力滞效应;随着荷载的增加,翼板腹板处应变与相邻测点差值增大;截面F-F的剪力滞系数全部小于1,翼板腹板处剪力滞系数最小,向两侧逐渐增大,随着荷载的增加,剪力滞系数逐渐增大,但不超过1.

(a) 上表面应变 (b) 剪力滞系数
由图5,6可知:集中荷载和均布荷载作用时,截面F-F腹板处翼板均为正剪力滞效应,但该处剪力滞系数均小于1,表明不可简单地根据剪力滞系数判断剪力滞效应的正负,剪力滞系数仅代表实际应力与理论应力之比,与正负剪力滞效应无直接关系.
截面E-E距左侧支座220 mm(L/4).集中荷载作用下,截面E-E翼板上表面应变及剪力滞系数,如图7所示.由图7可知:各级荷载作用时,翼板腹板处应变均大于相邻两测点应变,且随荷载的增大,应变差值逐渐增大,至第4级荷载作用时,应变差值接近100×10-6;该截面剪力滞系数均大于1,为正剪力滞效应,翼板腹板处剪力滞系数最大,向两侧逐渐减小,随着荷载增加,剪力滞系数逐渐减小,即正剪力滞效应逐渐减弱.

(a) 上表面应变 (b) 剪力滞系数
均布荷载作用下,截面E-E翼板上表面应变及剪力滞系数,如图8所示.由图8可知:翼板腹板处与相邻两侧无较大应变差值,最大差值为第4级荷载作用时的10×10-6;剪力滞系数在翼板腹板处一定范围内大于1,向两侧逐渐减小至小于1,第1,2,3级荷载作用时,剪力滞系数随着荷载的增加逐渐增大,最大值为第3级荷载荷载作用时的1.25,即正剪力滞效应逐渐增强,但当第4级荷载作用时,剪力滞系数整体小于第3级荷载,但大于第2级荷载,为1.21.施加荷载后,T形简支梁腹板底部受拉,翼板上表面受压,翼板与腹板交界面产生的剪切力通过肋板传递给翼板,剪切力在翼板上分布不均匀,在靠近腹板处最大,远离腹板逐渐减小.因此,剪切变形沿翼板分布不均匀,引起弯曲时远离腹板的翼板的纵向位移滞后于靠近腹板的翼板的纵向位移,即正剪力滞效应.截面E-E远离支座截面,支座反力对截面的负剪力滞效应有限,该截面为正剪力滞效应.

(a) 上表面应变 (b) 剪力滞系数
截面D-D距左侧支座300 mm(L/3),属于纯弯段.集中荷载作用下,截面D-D翼板上表面应变及剪力滞系数,如图9所示.由图9可知:在各级荷载作用下,翼板腹板处的应变无较大差值;截面D-D的剪力滞系数在翼板腹板处大于1,仅有靠边缘两侧翼板的剪力滞系数小于1,最大值为第1级荷载作用下的1.13,为正剪力滞效应;随着荷载的增加,剪力滞系数逐渐减小,即正剪力滞效应逐渐减弱.

(a) 上表面应变 (b) 剪力滞系数
均布荷载作用下,截面D-D翼板上表面应变及剪力滞系数,如图10所示.由图10可知:翼板腹板处应变与相邻两测点在各级荷载作用时无较大差值,剪力滞系数仅在翼板腹板处及相邻两测点大于1,最大值为1.05,即正剪力滞系数;随着荷载的增加,剪力滞系数逐渐较小.综上可知,两种荷载作用下,同一级荷载时,剪力滞系数均向两侧逐渐减小.

(a) 上表面应变 (b) 剪力滞系数
2.2 结果分析
不同荷载形式、不同等级荷载作用下,各截面翼板腹板处的剪力滞系数,如表2所示.由于截面G-G位于支座截面,弯矩为0,故无法计算其剪力滞系数.

表2 各截面翼板腹板处的剪力滞系数
集中荷载作用下,截面F-F为正剪力滞效应,从第1级荷载到第4级,剪力滞系数降低了8.3%,下降幅度较大.在实际工程设计中,需根据实际受力的大小,在靠近支座截面的翼板上表面适当布置受压钢筋.截面E-E为正剪力滞效应,从第1级荷载到第4级,剪力滞系数下降了2.5%.截面D-D为正剪力滞效应,从第1级荷载到第4级,剪力滞系数下降4.0%;其弯矩大于截面E-E,剪力小于截面E-E,属纯弯段;在各级荷载作用下,截面D-D的剪力滞系数均小于截面E-E.由此可知,纯弯段剪力滞系数小于相邻截面剪力滞系数,但随着荷载增加,剪力滞系数的降幅较大.截面C-C,D-D均属纯弯段,剪力滞系数降幅相比截面E-E较小.根据加载点位置判断,截面B-B与截面E-E属对称位置,性质相同不赘述.
均布荷载作用时,截面F-F为正剪力滞效应,随着荷载的增加,剪力滞系数逐渐增大,其变化趋势与集中荷载作用时相反;截面F-F的剪力滞系数整体偏小,最小值为第1级荷载作用下的0.485 5,这是因为截面F-F靠近简支梁支座截面,支座反力约束较强,导致实测应变值较小,而理论计算所得应变值未考虑支座反力的影响.截面E-E为正剪力滞效应,其剪力滞系数随荷载的增加,先逐渐增大,后逐渐减小,最大值为第3级荷载作用时的1.245 6,最小值为第4级荷载作用时的1.210 3.截面D-D的剪力滞系数随着荷载的增加而逐渐减小,从第1级荷载到第4级,剪力滞系数下降了1.2%,降幅较小;其弯矩大于截面E-E,剪力小于截面E-E,剪力滞系数整体小于截面E-E.截面C-C仍为正剪力滞效应,剪力滞系数随荷载的增加而减小,从第1级荷载到第4级,剪力滞系数降低了2.6%.截面B-B剪力为负值,剪力滞系数随荷载的增加而逐渐减小,从第1级荷载到第4级,剪力滞系数下降4.2%.结合截面D-D,C-C,B-B的数据可知,剪力滞系数的变化趋势与剪力的正负无关.
3 有效翼缘宽度算例
由于剪力滞效应的存在,使靠近腹板处的翼板受力较大,应力较集中.为了在计算中应用初等梁理论计算方法,引入有效翼缘宽度的概念.
实际工程中,梁的受力以均布荷载为主,以本试验为例,计算T形简支梁在不同等级荷载作用时的有效翼缘宽度.T形简支梁示意图,如图11所示.图11中:t,tw分别为翼板、腹板的厚度;b为翼板宽度;σmax为翼板最大正应力;h1,H1,H2分别为中性轴距翼板中心、上表面、下表面的距离;翼板最大正应力σmax的虚线所示面积等于实际应力曲线包围面积,虚线矩形面积的边长就是翼缘的有效宽度(bf′),其表达式为

图11 T形简支梁示意图
(3)
横截面上相应于翘曲位移的翘曲正应力(σw)为
上式中:D为附加于梁全截面的均匀纵向翘曲位移;U(x)为广义位移函数.
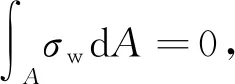
即得
D=-3bt/(2A).
上式中:A为T形简支梁的全截面面积.
由文献 [16],[17]可得剪力广义位移微分方程和应力表达式分别为
(4)
(5)
承受均布荷载的T形简支梁,如图12所示,其弯矩M(x)和剪力Q(x)的函数表达式分别为

图12 承受均布荷载的T形简支梁
非固定端支座的边界条件为U1|x=L/2=U2|x=L/2.
将Q(x)代入式(2),再由边界条件可得均布荷载作用下T形简支梁的有效翼缘宽度为
计算可得均布荷载作用下T形简支梁翼板的最大正应力和有效翼缘宽度,如表3所示.

表3 均布荷载作用下T形简支梁翼板的最大正应力和有效翼缘宽度

4 结论
通过有机玻璃T形简支梁试验,研究T形梁不同截面应变和剪力滞系数的大小,分析剪力滞传递的机理,利用公式计算有效翼缘宽度,探究不同剪力滞效应对有效翼缘宽度的影响,得出以下4点结论.
1) 集中荷载作用下,翼板存在明显的剪力滞现象,靠近支座截面存在负剪力滞效应,剪力滞系数沿腹板向两侧逐渐增大,距左侧支座L/4截面处开始出现正剪力滞效应,且该截面剪力滞系数均大于1,实测最大剪力滞系数为1.22,沿腹板向两侧逐渐减小,在纯弯段出现正剪力滞效应,但效应不明显.
2) 均布荷载作用下,靠近支座截面为负剪力滞现象,且剪力滞系数均小于1,距左侧支座L/4截面为正剪力滞效应,剪力滞系数在1上下浮动,实测最大值为1.25.与集中荷载作用相比,均布荷载作用时的剪力滞系数普遍较小,且降幅不大.
3) 剪力滞系数的变化趋势与剪力的正负无关,随着弯矩的增加,同一截面的剪力滞系数降幅逐渐增大.
4) 正剪力滞效应作用时的有效翼缘宽度为正,同一截面位置处的T形简支梁的有效翼缘宽度与该截面的正应力大小无关,不同截面的有效翼缘宽度受剪力影响较大.
