基于BP神经网络模型的柔性喷管动力学仿真

薛牧遥，胡嘉鑫，张金尧，童 悦，李修明，郑 庆，任军学

(1 上海航天动力技术研究所，上海 200125;2 北京航空航天大学宇航学院，北京 100191)

0 引言

为实现导弹轨道调整与姿态控制，以柔性喷管为代表的推力矢量控制装置目前已得到了广泛应用。柔性喷管推力矢量系统主要由柔性接头、活动体、固定体以及与之相匹配的伺服控制系统所组成[1-6]。在柔性喷管推力矢量控制系统中，柔性接头对整个系统的动态特性起着决定性作用。柔性喷管是一种典型的非线性迟滞系统。由于柔性接头中的橡胶弹性件具有粘弹性特性，柔性接头在摆动时会在摆动角度和恢复力矩间产生迟滞现象[2]，并且迟滞曲线受到摆动振幅、摆动频率、工作压强、环境温度[2-3]等因素的影响，使得其动态特性十分复杂。准确描述柔性喷管在不同条件下的迟滞曲线，对于控制系统的精确控制有着重要意义。

描述迟滞现象的典型物理模型有定刚度定阻尼模型[5]、线性粘性阻尼模型[6]、混合阻尼模型[7-8]等。其中，定刚度定阻尼模型忽略了摆动振幅、频率、工作压强等条件对力矩的影响，不能满足柔性喷管推力矢量控制系统精确建模的需要；线性粘性阻尼模型适应柔性喷管摆动力矩，但在不同工况的能力(即泛化能力)方面仍然不足[6]；混合阻尼模型具有较好的泛化能力，但存在高频情况下阻尼成分系数发散的问题[7-8]。

神经网络模型由于具有逼近任意非线性函数，且不需要给出具体函数形式的优点，近年来被用于非线性迟滞系统建模中[9-10]。其中，误差逆传播(BP)神经网络模型结构简单，自适应能力强，应用更广泛。因此，将基于BP神经网络模型构造柔性喷管迟滞曲线模型，并结合伺服机构模型对柔性喷管进行动力学仿真，以实现对柔性喷管摆动的精确描述。

1 柔性喷管动力学模型建立

1.1 BP神经网络模型

BP神经网络通常是指由一层输入层、若干层隐含层、一层输出层组成，并采取误差逆传递学习算法进行权值和阈值修正的前向网络[11]，如图1所示。在BP神经网络模型中，各层之间采取全联接，层内无连接，输入层即为当前时刻的自变量，通过隐含层计算，并由输出层得出最终输出值。

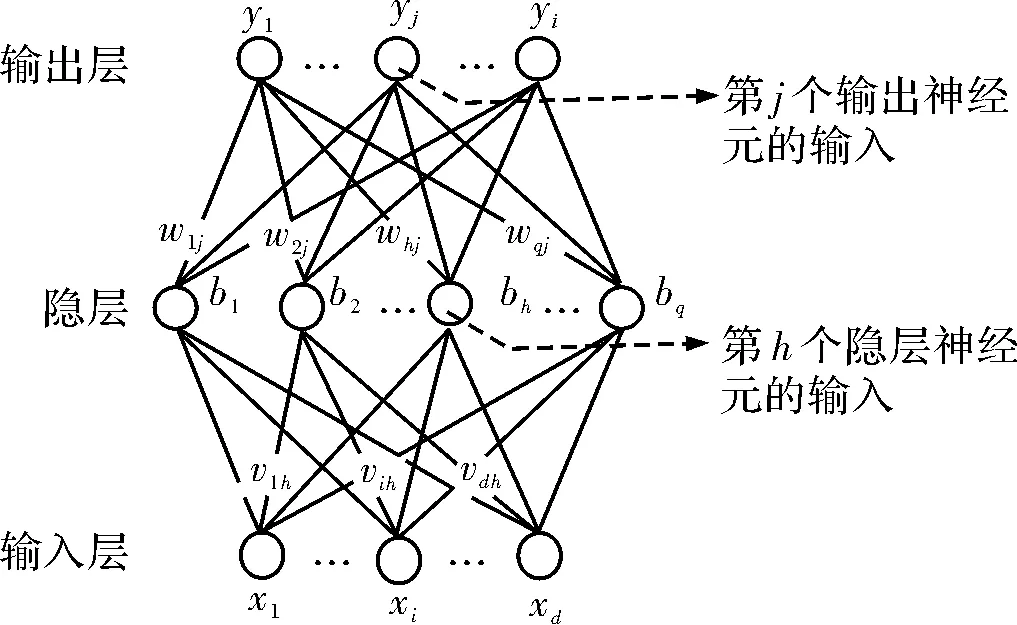
图1 BP神经网络模型示意图

由于柔性喷管迟滞曲线主要受摆动振幅、摆动频率、工作压强影响，而迟滞曲线的恢复力矩则主要由当前的摆动角度和摆动速度决定[2]。则以摆动振幅、摆动频率、工作压强、摆动角度以及摆动速度作为输入变量，即此时输入层神经元个数为5。而输出层节点个数则取决于网络目标输出变量的个数，需要研究的关系为柔性喷管迟滞曲线恢复力矩与摆动振幅、摆动频率、工作压强、摆动速度以及摆动角度的关系，即此时输出层输出变量为迟滞曲线恢复力矩，输出神经元个数为1。

采取三层神经网络，即只含有一层隐含层，默认取10个神经元，输入层与隐含层之间采取Sigmoid传递函数用于保证网络可以逼近非线性函数，隐含层与输出层之间则采取线性传递函数以达到任意输出值[11]。此外训练函数取Levenberg-Marquart propagation法以避免计算Hessian矩阵从而加快计算速度[12]。为了减弱过拟合的影响，在训练时还将输入样本随机分为训练集、验证集和测试集3部分，比例分别为70%，15%，15%。当训练集误差持续降低，同时测试集误差不断增加时，则停止训练，取训练集与实验数据误差最小所对应的权值和阈值作为网格结果。

1.2 电液伺服机构-柔性喷管神经网络模型

图2为电液伺服机构-柔性喷管模型示意图。采用神经网络模型描述柔性喷管模块，其余部分采用电液伺服机构模型。在柔性喷管模型中，输入参数为力矩，输出为角度。

图2 伺服机构-柔性喷管动力学模型

采用BP神经网络模型以摆动振幅、摆动频率、工作压强、摆动速度以及迟滞曲线恢复力矩为输入变量，以摆动角度为输出变量，所得电液伺服机构-柔性喷管神经网络模型示意图如图3所示。

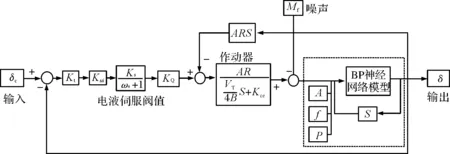
图3 电液伺服机构-柔性喷管神经网络模型示意图

以不同工作压强(0 MPa，3 MPa，6 MPa，9 MPa)、不同摆动振幅(2°，4°，6°)以及不同摆动频率(0.1 Hz，0.3 Hz，0.6 Hz，0.9 Hz)下迟滞曲线所对应的振幅、频率、压强、速度、摆动力矩作为输入变量。训练数据共计48组工况，8 841组输入样本，随机的分为70%，15%，15%的训练集、验证集与测试集，所得结果的均方误差和相关系数如表1所示。

表1 以摆动力矩为输入条件下的BP神经网络模型训练结果

2 仿真结果与分析

2.1 仿真结果及与实验曲线对比

图4～图6分别为不同摆动频率、摆动振幅和工作压强下，柔性接头摆动实验结果和电液伺服机构-神经网络模型仿真结果的对比。

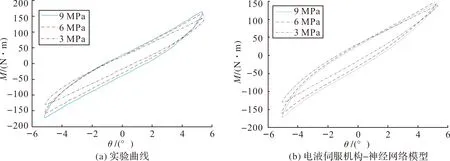
图6 不同工作压强下的迟滞曲线(5°,0.7 Hz)

由图4(a)可知，随着频率的增加，迟滞曲线所围成的面积稍有增大，在0°摆角位置的力矩略有增大，迟滞曲线先沿顺时针后沿逆时针方向发生了转动。由图4(b)可以看出，电液伺服机构-神经网络模型所构造的迟滞曲线形状可以准确的与实验结果相吻合，并符合实验曲线随频率变化的规律。

图4 不同摆动频率下的迟滞曲线(9 MPa,6°)

由图5和图6可以看出，电液伺服机构-神经网络模型所构造的迟滞曲线均与实验结果相吻合。

图5 不同摆动振幅下的迟滞曲线(6 MPa,0.5 Hz)

2.2 与物理模型的比较

为了与电液伺服机构-神经网络模型的预测和泛化能力进行对比，图7～图9给出了电液伺服机构-定刚度定阻尼模型和电液伺服机构-混合阻尼模型的预测结果。

图7(a)为不同摆动频率下，电液伺服机构-定刚度定阻尼模型的迟滞曲线。可以看出，随着频率的增加，迟滞曲线所围成的面积大幅增加，在0°摆角位置的力矩也大幅增大，并且迟滞曲线不发生转动，与图4(a)实验结果相差较大。图8(a)为不同摆动振幅作用下的电液伺服机构-定刚度定阻尼模型迟滞曲线，可以看出，随着振幅的增加，迟滞曲线并不发生转动，这与图5(a)实验结果相差较大。图9(a)为不同工作压强作用下的电液伺服机构-定刚度定阻尼模型迟滞曲线,可以看出，随着压强的增加，迟滞曲线并没有发生改变，与图6(a)实验结果相差较大。

图7(b)～图9(b)表明，电液伺服机构-混合阻尼模型所构造的迟滞曲线与实验结果相吻合。

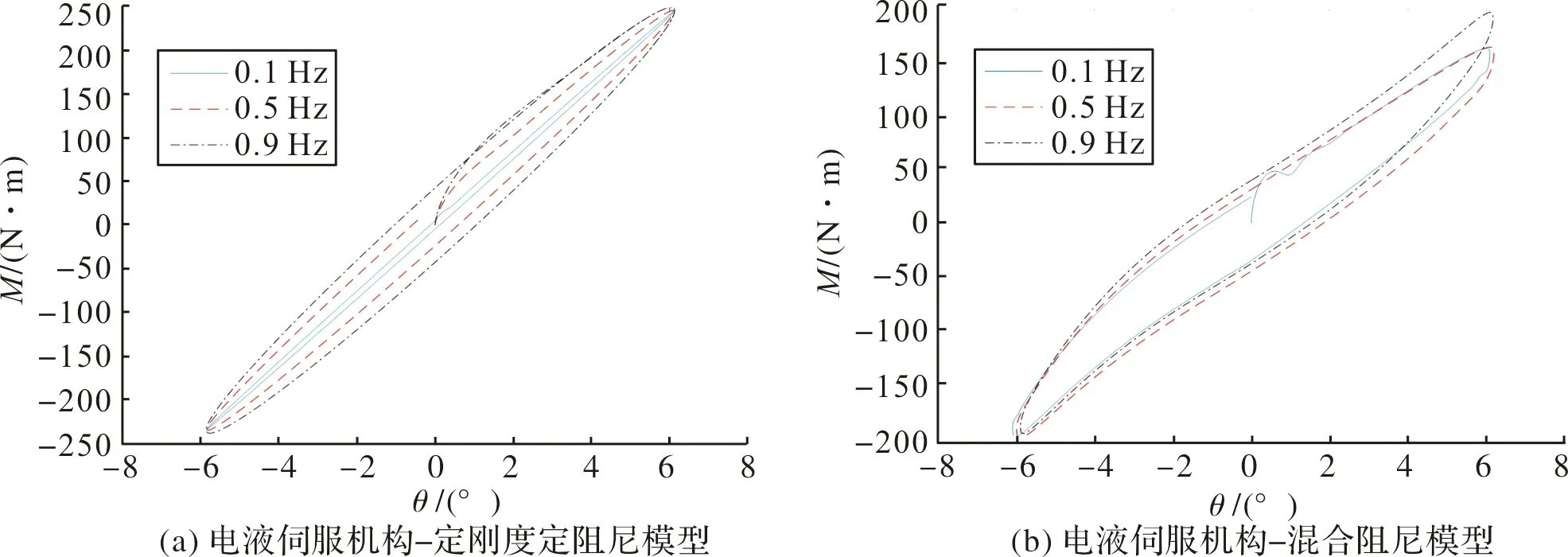
图7 不同摆动频率下两种物理模型迟滞曲线

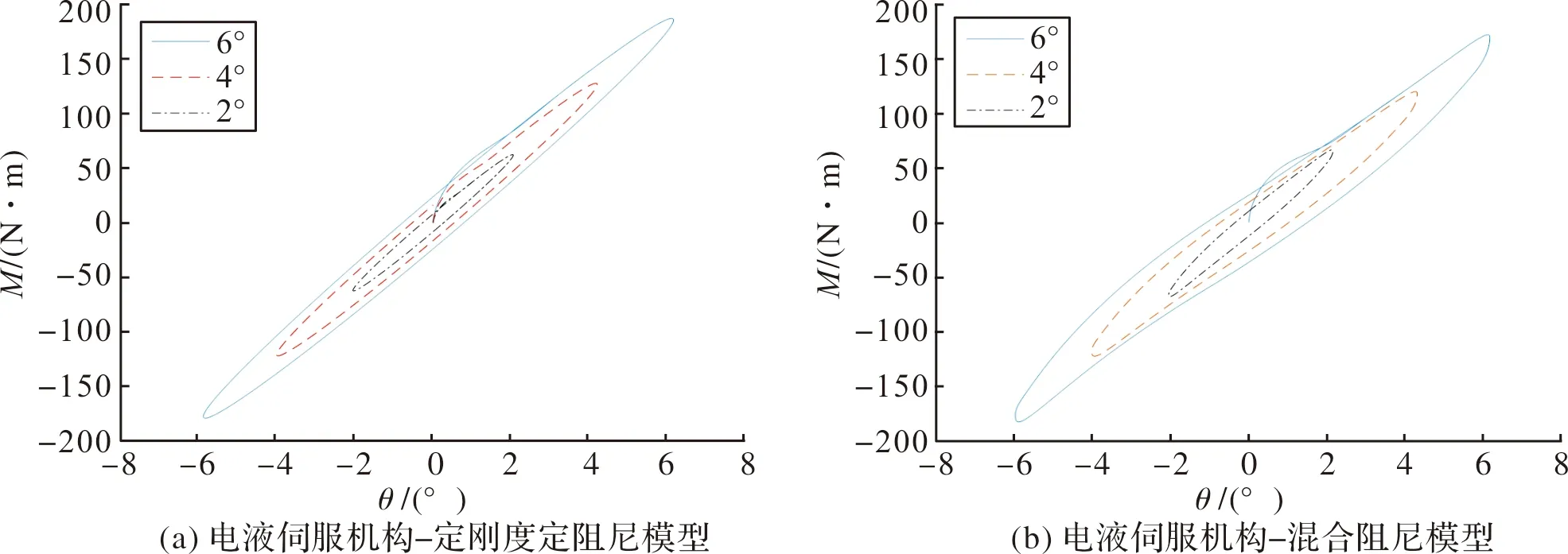
图8 不同摆动振幅下两种物理模型迟滞曲线

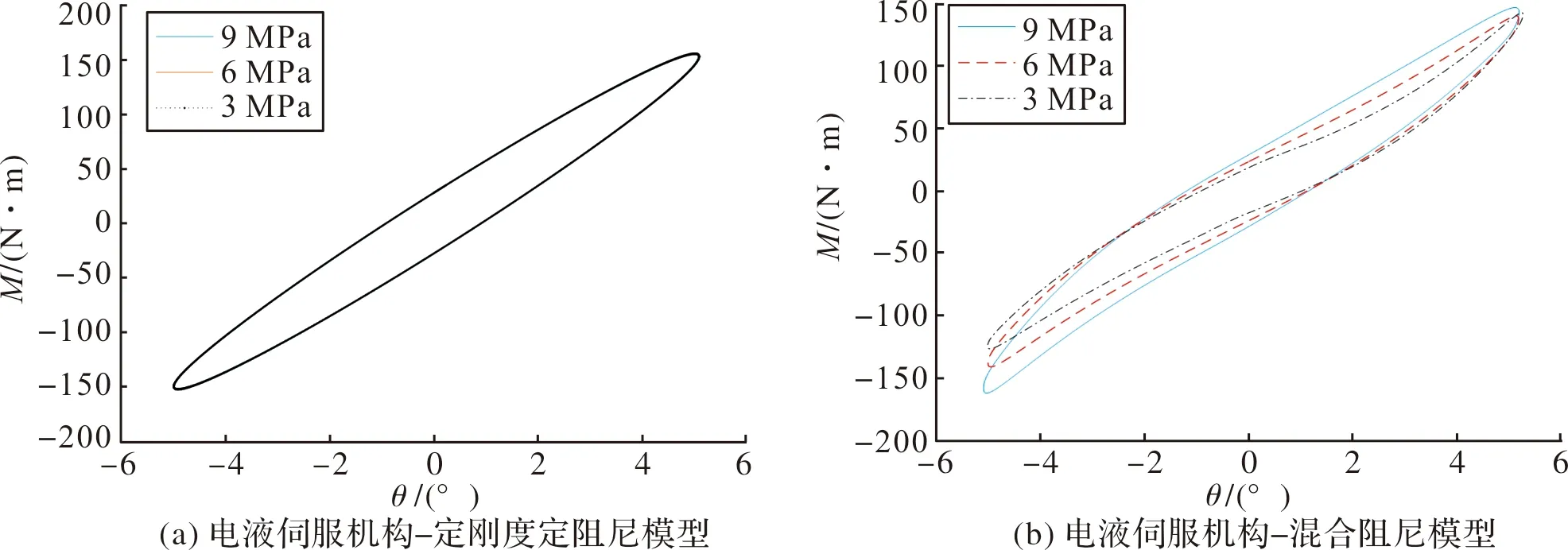
图9 不同工作压强下两种物理模型迟滞曲线

为进一步对比各模型的预测精度和适应能力，图10给出了不同工作条件下的BP神经网络模型、混合阻尼模型[7-8]、线性粘性阻尼模型[6]以及定刚度定阻尼模型[5]迟滞曲线预测误差的定量比较结果。这里定义相对误差e用来表示模型结果的预测误差，其表达式为：

(1)

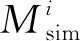
图10(a)、图10(b)、图10(c)分别代表：较大摆动振幅、摆动频率、压强，中等摆动振幅、摆动频率、压强以及较小摆动振幅、摆动频率、压强3种典型工况。由图10可以看出，BP神经网络模型在较广工作范围内的预测误差e1与混合阻尼模型预测误差e2相当(3.02%～8.52%)，远低于线性粘性阻尼模型误差e3和定刚度定阻尼模型误差e4(9.94%～40.71%)。

图10 不同工况条件下的模型迟滞曲线

图11给出了振幅为6°时电液伺服机构-神经网络模型的系统闭环幅频特性曲线和动态响应曲线。可以看出，随着频率的升高，振幅逐渐降低，系统带宽在10 Hz左右。需要指出的是，对于混合阻尼模型，当计算系统闭环幅频特性曲线时，其阻尼成分系数将会随着频率发生较大的变化，使得闭环幅频特性曲线发散[4]，而神经网络模型不存在此问题。因此，相比于上述3种物理模型，BP神经网络模型对柔性接头迟滞曲线的预测具有更好的适应性。

图11 电液伺服机构-神经网络模型的系统动态特性

为了比较不同模型对电液伺服机构-柔性喷管模型位置精度的影响，对电液伺服机构-混合阻尼模型、电液伺服机构-线性粘性阻尼模型、电液伺服机构-神经网络模型、电液伺服机构-定刚度定阻尼模型的位置精度进行了对比，如图12所示。

由图12可知，电液伺服机构-神经网络模型的位置精度比电液伺服机构-线性粘性阻尼模型、电液伺服机构-定刚度定阻尼模型的位置精度分别高0.02°～0.10°以及0.10°～0.15°，而此时神经网络模型对应工况条件下的仿真迟滞曲线相对误差比线性粘性阻尼模型和定刚度定阻尼模型小6.92%～13.68%以及19.01%～32.19%(参见图10)。此外，电液伺服机构-神经网络模型与电液伺服机构-混合阻尼模型具有相似的位置精度(最大误差为0.03°)，其原因是两模型具有相似精度的迟滞曲线模型结果(参见图10)。

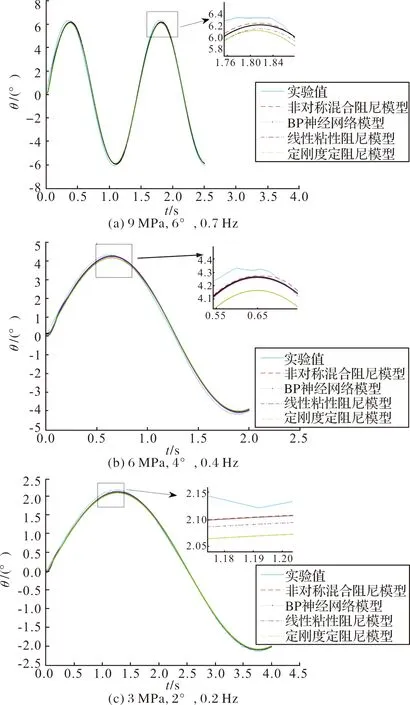
图12 不同工况和模型下的位置精度对比

3 结论

在BP神经网络模型的基础上，构造了电液伺服机构-柔性喷管神经网络动力学模型，通过与多种电液伺服机构-物理模型的仿真结果进行对比，结论如下：

1)电液伺服机构-神经网络模型结果符合实验结果随摆动振幅、摆动频率、工作压强的变化规律,可以很好的与实验结果相吻合。

2)相比于物理模型，电液伺服机构-柔性喷管的神经网络模型具有更好的精度和泛化能力。

3)由于神经网络模型具有较高的迟滞曲线预测精度，电液伺服机构-神经网络模型相比物理模型的位置精度可以提高。