基于超声波测距和多普勒测速的室内无人机跟踪定位算法

2021-07-30黄婷，徐明

弹箭与制导学报 2021年3期

关键词：接收端测距室内环境

黄婷，徐明

(江西财经职业学院南昌校区信息中心，南昌 331700)

0 引言

随着电子通信技术的发展，无人机(UAV)已在环境监测，农业植保，影像航拍等多个领域中广泛使用[1]。位于地面上的控制基站通过向无人机的航行控制器发送指令，使无人机依据用户的指令飞行。因此，控制基站需实时对无人机进行定位和跟踪。

目前，借助于全球定位系统(GPS)和无人机的惯性测量装置(IMU), 控制基站能够方便对室外环境的无人机进行定位跟踪[2]。然而，由于GPS在室内环境的定位精度低，对室内环境的无人机进行定位跟踪存在挑战。

针对室内环境的无人机定位问题，研究人员提出多种定位算法。其中基于视觉定位算法受到广泛关注[3]，但由于无人机在飞行中的震动，基于视觉定位算法的精度并不高。研究人员提出了其他的定位算法，如基于射频定位[4]、基于多普勒频移跟踪[5]以及基于蜂窝网络跟踪等[6]。但是在室内环境，蜂窝网络信号不稳，容量受到环境影响。

超声波测距和多普勒测速的跟踪定位算法(TLUD)先估计超声波信号的到达时间差ToA[7]，利用跳频扩频(FHSS)技术消除室内多径衰减的影响，提高基于ToA的测距精度，利用卡尔曼滤波估计实现实时测距，并利用多普勒频移估计无人机的移动速度。仿真结果表明，提出的TLUD算法有效提高了室内定位精度。

1 TLUD定位跟踪算法

系统模型如图1所示，无人机在室内飞行，通过WI-FI与终端用户进行数据通信。无人机内安装了超声波发射器，周期地传输超声波信号。接收终端收集数据，并执行定位算法，最终对无人机进行定位跟踪。

图1 系统模型

1.1 基于ToA的测距

无人机发射信号，经二相相移键控(BPSK)调制[8]，再通过扩频传输至用户。BPSK调制有两个变化的状态，一个状态表示一位比特信息。如用相位+90°表示1，相位-90°表示0。如图2(a)所示。令S(t)表示无人机发射的BPSK调制信号，其表达式为：

S(t)=b·T(t)·sin(2πfmt+φ)

(1)

式中：b为数据符号；T(t)为矩形脉冲函数；TB为矩形脉冲的宽度，当0≤t≤TB，T(t)=1，否则为零，如图2(b)所示；fm为信号跳频点的频率集；φ为初始相位。

图2 BPSK和矩形脉冲信号

信号S(t)经多径信道传输至接收端,接收端所接收的信号r为：

r(t-τ)=d·T(t-τ)·sin(2πfm(t-τ)+φ)+M(t)+N(t)

(2)

式中：τ为传输时延；M(t)为多径衰落的影响;N(t)为高斯噪声。M(t)可表示为：

(3)

式中：αi为第i条路径的信号衰减；τi为第i条路径信号的时延。多径衰弱在室内环境无法避免。为此，利用FHSS技术[9]消除多径衰弱，进而提高对时延τ的估计。因此，式(2)可转换成：

r(t-τ)=b·T(t-τ)·sin(2πfm(t-τ)+φ)+N(t)

(4)

接下来，利用广义互相关估计时延τ，令R1,2(τ)表示信号S(t)与r(t-τ)的互相关值，其表达式为：

R1,2(τ)=E{S(t)·r(t-τ)}

(5)

(6)

1.2 基于多普勒频移测速

当信号接收端与发送端间相对位置发生移动时，信号频率就发生偏移。令Fs表示频移的频率，其表达式为：

Fs=(υ/c)F0

(7)

式中：F0为原始信号频率；υ为相对于发送端的接收端的相对速度；c为声波的传输速度。

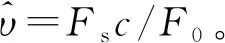
1.3 基于Kalman滤波的测距修正

充分利用所测的距离和1.2节所测的速度信息，Kalman滤波实时地估计无人机与控制基站(接收端)间的距离。令Dk表示在第k个时间窗口内，无人机与控制基站的实际距离：

(8)

(9)

(10)

式中：σk，ζk分别为nk，ωk的标准方差。

1.4 基于泰勒级数展开的最小二乘法的无人机位置估计

令(x,y,z)表示无人机位置。估计三维坐标的位置，至少需要建立3个方程：

(11)

式中：i=1,2,3。di表示第i个超声波接收端离UAV的距离。该距离是依据式(10)所估计距离。

1.4.1 基于最小二乘法的位置估计

考虑到测距误差，di3总是与实际值存在误差。若只依据式(11)所构建的3个方程求解无人机位置，位置误差会较大。为此，增加方程数量，并利用基于泰勒级数展开的最小二乘法求解，进而提高位置估计的精度。

4S的营销战略告诉我们从消费者需求出发，打破传统的追求市场占有率营销模式，建立起一种全新的“消费者占有”的营销导向。通过满意(satisfaction)、服务(SERVICE)、速度(speed)以及诚意(sincerity)四个方面来不断满足消费者的消费需求。要求对产品、服务、品牌不断进行综合性消费者满意指数和消费者满意级度的测评与改进，以服务品质最优化，使消费者满意度最大化，进而达到消费者忠诚的“指名度”，同时强化了企业的抵御市场风险经营管理创新和持续稳定增效的“三大能力”。

建立4个方程,即在空间内部署4个超声波接收端，并由这4个接收端离无人机的距离，估计无人机的位置。因此，结合式(11)可得:

(12)

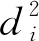
X=(ATA)-1ATB

(13)

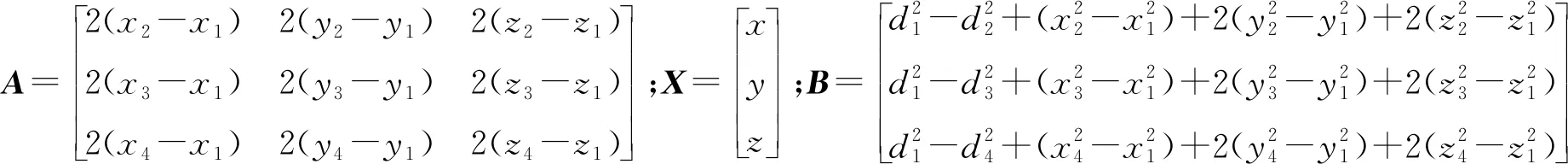
1.4.2 基于泰勒级数展开

对式(12)进行线性化处理丢失了一部分测距信息，这可能降低了估计精度。为此，再利用泰勒级数展开，进一步估计无人机的位置。

考虑到式(12)为2阶方程组，先对式(12)进行开方运算，再改写成关于x,y,z的函数得：

(14)

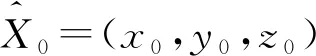
(15)

经简化整理可得：

MX=L+E

(16)

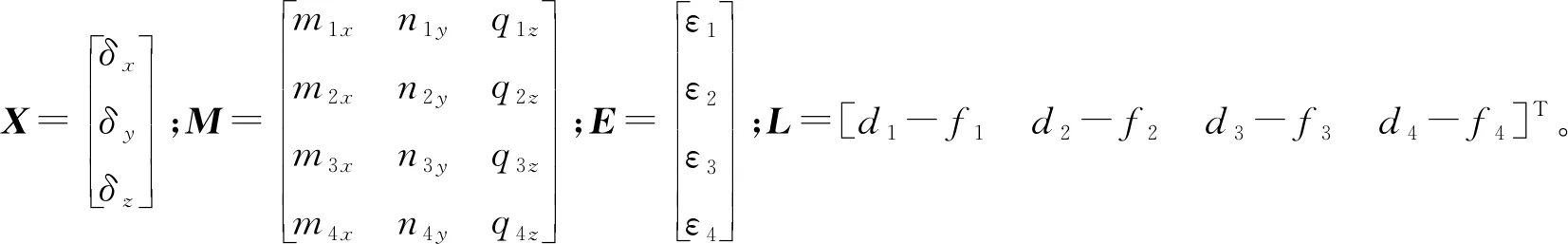
X=(MTQ-1M)-1MTQ-1L

(17)

2 性能分析

2.1 仿真环境

利用MATLAB软件建立仿真，分析TLUD算法的性能。在5 m×5 m×3 m的房间内部署一个无人机和4个超声波接收端(4个智能手机)。4个智能手机的位置分别为：(2.5,0,1.5)，(5,2.5,2.5)，(2.5,5,2)和(0,5,3),单位为m。无人机在室内随机飞行。

在无人机内部安装一个超声波发射器，并由该发射器传输FHSS信号。频率范围为25～55 kHz。抽样频率fs=340 kHz。在25～55 kHz频率区间内选取6个子频率(跳频)：27.5 kHz,32.5 kHz,37.5 kHz,42.5 kHz,47.5 kHz和52.5 kHz。每个子频的的带宽为5 kHz。