后框独立驱动式双框架位标器的指向分析

汤海亮，陈余辉，席 斐，朱全发，屈军利

(西安导引科技有限责任公司，西安 710065)

0 引言

目前导引头位标器大都采用框架结构来实现导引头俯仰-方位角运动，以其框架角范围大、隔离扰动能力强而广泛应用[1]。包括单框架和双框架两种形式：单框架位标器的内外框均采用力矩电机直驱、电位计或旋变进行测角，形式为万向支架；双框架位标器将驱动或者测角部件与内外框架平行轴分离后置安装，采用平行四边形机构实现驱动力矩或框架角位移传递。相比单框架位标器，双框架位标器更适用于导引头小口径、结构紧凑、类锥外形且框架角要求大的场合，尤为适用红外、雷达及复合类大尺寸探测部件的配备需求[2-4]。

单框架位标器的指向角等于驱动角，吕常波等[5-6]研究了装调误差对滚仰式导引头视轴指向的影响，在装调层面对万向支架式位标器的指向精度进行了深入分析。周琼等[2]设计的大跟踪场图像导引头位标器就是双框架位标器的前后框均采用万向支架式连接，且前内框-后内框、前外框-后外框通过连杆连接分别形成两组平行四边形机构，其前框指向角与后框驱动角相等，采用这种结构形式，保证了前后框内环的同步运动。

文中所述的后框独立驱动式双框架位标器即是：位标器的前框采用万向支架式连接，后内环与后外环分别通过一根连杆与前内环、前外环连接，区别于前述双框架位标器，此形式后框的内外环相互独立。设计中发现，采用这种连接形式时前内环的指向角与后内环的驱动角不相等，建立了后框独立驱动式双框架位标器的几何模型，通过运动仿真确立了前后内环运动的非线性。利用坐标变换和位标器前后框的空间几何关系，得到了前框指向角与后框驱动角、内框连杆长度及后内环摇臂长度的函数关系；通过对函数方程进行数值求解，定性分析了前框指向角随后框驱动角的变化趋势，彻底解决了此形式位标器的指向问题。

1 后框独立驱动式双框架位标器几何模型

后框独立驱动式双框架位标器的前框采用万向支架式连接，后内环与后外环分别通过一根连杆与前内环、前外环连接，此形式后框内外环相互独立，由两个力矩电机分别驱动的内外环摇臂组成，两个测角元件分别与两个力矩电机同轴固连，这样由外环摇臂-外框连杆-前外环-本体、内环摇臂-内框连杆-前内环-本体形成两个四连杆机构，前者为平行四边形四连杆机构，后者为空间四连杆机构。后框独立驱动式双框架位标器几何模型如图1所示。

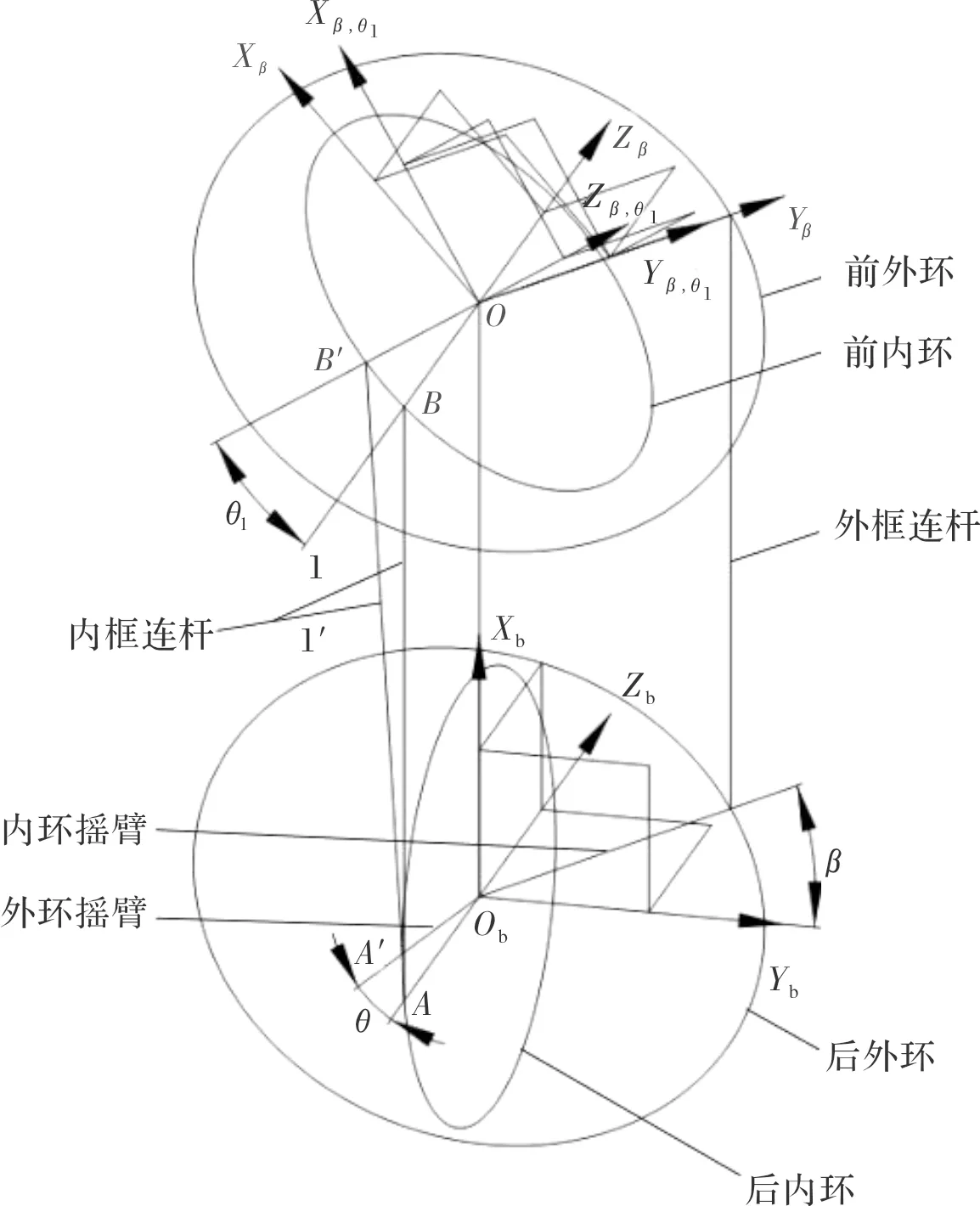
图1 后框独立驱动式双框架位标器几何模型

2 坐标系及参数定义

如图1所示，设外框连杆、内框连杆长度均为l(与本体机架长度相等)，内环摇臂长度为r。

后框坐标系Ob-XbYbZb。原点Ob取两个力矩电机轴线的交点。ObXb轴和导引头的纵轴重合，方向指向导引头头部。Yb轴与外环驱动电机轴线重合，和Xb轴垂直，图示向右为正。Zb轴和Xb轴与Yb轴成右手系。可知后框坐标系是通过弹体坐标系平移得到，此不赘述。

前框外环坐标系O-XβYβZβ。原点O取前内环与前外环旋转轴线的交点。由后框坐标系Ob-XbYbZb经过平移l后绕Zb轴旋转一个角度β后得到，即是外环摇臂转动一个角度β后引起前外环同步转动。

前框内环坐标系O-Xβ,θ1Yβ,θ1Zβ,θ1。在前框外环坐标系O-XβYβZβ的基础上，内环摇臂再转动一个角度θ后引起前内环绕Yβ轴转动一个角度θ1后得到。

各坐标系的变换关系[7]如图2所示。

图2 各坐标系之间的变换关系

3 指向分析

3.1 坐标变换矩阵

采用旋转矩阵[8](旋转向量)实现三维空间坐标变换。

以世界坐标系到相机坐标系的变换为例，旋转的欧拉角从世界坐标系转换到相机坐标系，先绕z轴旋转，再绕y轴旋转，之后绕x轴旋转，最终得到相机坐标系，角度分别是φy、φp、φr。

从相机坐标转换的世界坐标实际上是反变换过程，通过定义Rx反旋转将相机坐标反旋转过来，之后依次绕y,z轴反旋转，从相机坐标系到世界坐标系的旋转矩阵按如下方式定义：

(1)

(2)

(3)

因此，相机c坐标系到世界w坐标系间的旋转矩阵为：

(4)

对于平移矩阵为相机坐标系原点在世界坐标系下的坐标T，最终得到的坐标变换方程为：

Xw=RzRyRxXc+Tc，w

(5)

其中对z，y，x方向的旋转按照右手系定则，大拇指指向轴线方向，四指方向为旋转的正方向。

3.2 前框指向角与后框驱动角函数关系

由第1节的论述，后框独立驱动式双框架位标器的俯仰指向角与其后框的外环摇臂驱动角相等，即β′=β。下面主要分析此形式位标器偏航角与其后框的内环摇臂驱动角的关系。

接第2节，得到前框外环坐标系O-XβYβZβ后，此时内框连杆的位置保持在状态1处，两端点记为A，B。得到前框内环坐标系O-Xβ，θ1Yβ,θ1Zβ,θ1时，内环连杆运动到状态1′处，两端点记为A′，B′。则O-XβYβZβ下B点的坐标可记为(0，0，-r)，Ob-XbYbZb下A′点的坐标可记为(rsinθ，0，-rcosθ)。记平移向量l=(l，0，0)T，lOB′为从O到B′的向量，lOB为从O到B的向量，lA′B′为从A′到B′的向量，由3.1节坐标变换理论可得：

lOB′=Rzb·Ryβ·lOB+l

(6)

其中：

则lA′B′=lOB′-lOA′。

内环连杆的长度l保持不变，则有：

l2=lA′B′·lA′B′

(7)

解式(7)便可得θ1与l，r，θ，β的关系式。

4 数值仿真

由第3节的论述可知，式(7)是θ1关于l，r，θ，β的隐函数关系式，即f(θ1,θ,β,l,r)=0，式中还存在三角函数，所以得到θ1的解析式比较困难，下面对后框独立驱动式双框架位标器的偏航角θ1在不同后框外环摇臂驱动角β下与其后框的内环摇臂驱动角θ的对应关系进行数值计算[9]。

为了便于分析，取l=100 mm，r=50 mm。取β=(0，12.5，25，37.5，50)×π/180(θ1是关于β的偶函数，所以这里仅对β的正向进行分析)，在Matlab中绘制出θ1关于θ(θ∈[-20,20]·π/180)的函数图像如图3所示,β,θ的单位为(°)。

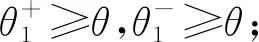
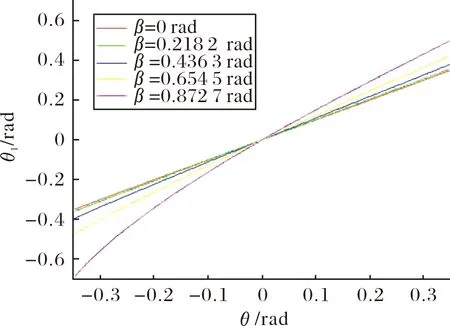
图3 位标器偏航角与内外环驱动角的关系曲线

此外，随着β的增大，θ1与θ的差值越来越大。表1中列举了不同β值时，θ值下θ1值。

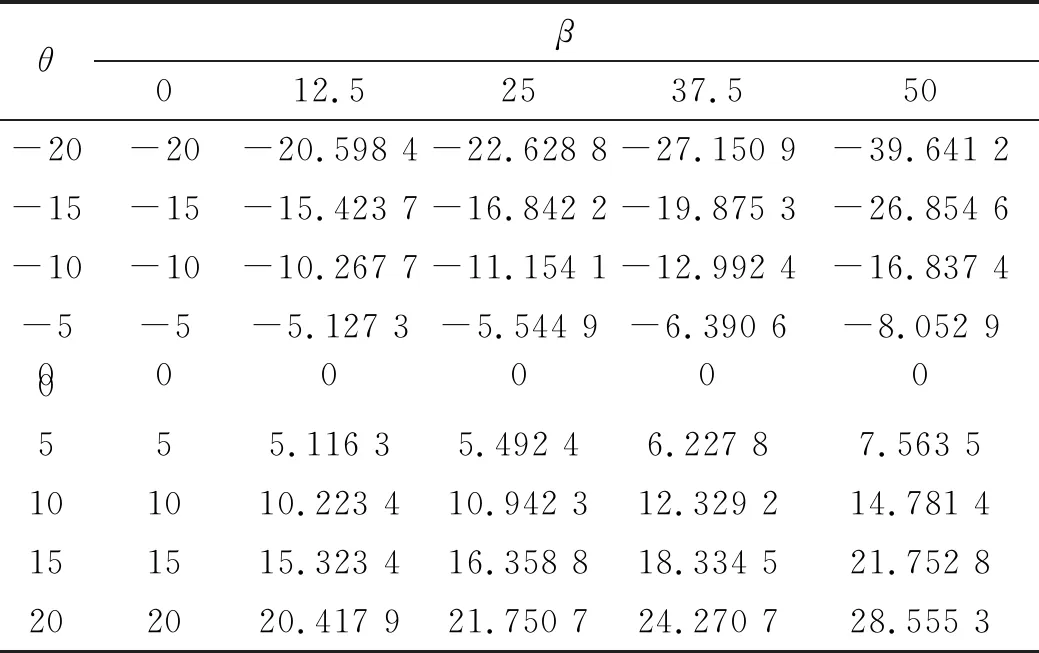
表1 前框偏航指向角θ1计算结果 单位：(°)

5 运动仿真结果对比

为了验证分析的正确性，在三维CAD软件建立后框独立驱动式双框架位标器的简易运动仿真模型，如图4所示。在UG(Unigraphics NX)中通过同轴、接触、对称、替换位置等约束实现内外环摇臂绕本体固定轴、前内环绕前外环、前外环绕本体的旋转运动，且实现外框连杆独立时各端一个旋转自由度、内框连杆独立时各端两个旋转自由度加连杆轴向的一个旋转自由度。

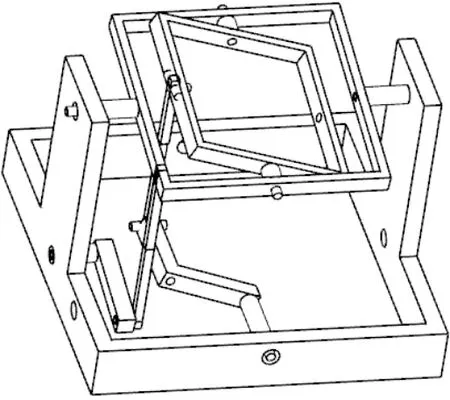
图4 后框独立驱动式双框架位标器简易运动仿真模型

当后内环摇臂及后外环摇臂施加角度约束后，前内环、前外环立即随动到一定角度，那么测量前内环与前外环两个框架平面的夹角就可得位标器的偏航指向角。仿真测量结果见表2，β=0时的结果忽略。

对比表1中各θ1与表2中各θ′1的数据可以看出，两者中的个别数据仅在小数点后第四位略有不同，其它数据完全相等。个别数据的细微差异是由于数值计算的精度导致的，所以文中对后框独立驱动式双框架位标器指向问题的分析结果完全正确。

接第4节分析，随着β，θ的增大，表2中β=50°、θ=-20°时，θ1已达到-39.641 2°，几乎是其θ的两倍，此时若用θ代替θ1作为位标器偏航角完全不可取。鉴于此形式θ与θ1存在巨大差异，所以位标器的偏航指向角不能用后内环驱动角替代。此外，在设计此形式位标器之初，可根据导引头对位标器的框架角(即指向角)要求及导引头尺寸要求反向估计其位标器后框内外环驱动角的大小，这对驱动测角部件的选型及位标器设计有重要意义。

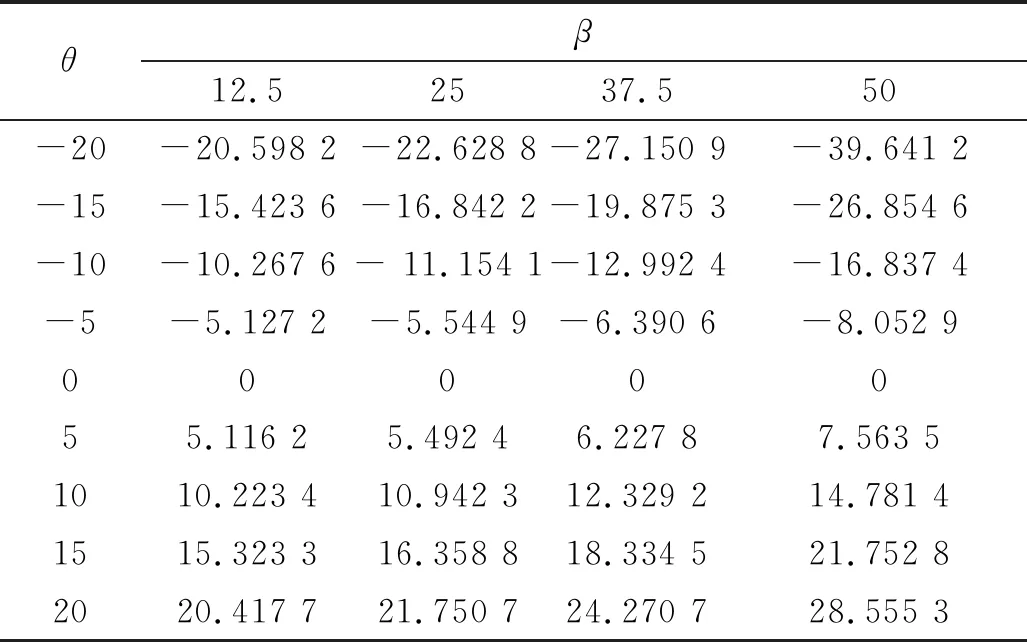
表2 θ′1仿真结果 单位：(°)

6 结论

通过理论分析、数值计算及运动仿真对后框独立驱动式双框架位标器的指向问题做了详细论述。

1)建立了后框独立驱动式双框架位标器的几何模型，分析了该形式位标器前后框、内外环的坐标变换关系及运动传递路径，得出了前框指向角与后框驱动角函数关系。

2)采用数值计算，得到了位标器偏航角与内外环驱动角的关系曲线，并通过典型角度数据的表格列举，定性、定量两方面分析了此形式位标器前框偏航指向角随后框驱动角的变化趋势及前框偏航指向角与后内环驱动角的差异。

3)运动仿真结果表明：本文针对后框独立驱动式双框架位标器指向问题的分析是正确的，位标器的偏航指向角不能用后内环驱动角替代。

为采用此形式位标器的导引头的指标分解、伺服控制及其位标器结构设计提供了设计依据，具有较高的工程应用价值。