一种低复杂度的超高阶码索引调制方法
2021-07-29冯永新
刘 芳 冯永新
①(沈阳理工大学信息科学与工程学院 沈阳 110159)
②(沈阳理工大学研究生院 沈阳 110159)
1 引言
直接序列扩频[1,2]具有抗多径、抗干扰、适应高动态环境[3]等优势,然而其优势都是以展宽信号频谱为代价的,从而引发了带宽利用率低以及信息传输率受限等问题。因此,应对高信息传输应用需求的提高,出现了多进制扩频(软扩频)[4,5]以及MBOK技术[6–8],其伪码都是由多个正交码集组成,每个码字映射若干比特信息,由于这部分信息是通过映射传输,并没有调制传输,所以信息传输率和频带利用率有所提高。基于多进制扩频,又出现了并行组合扩频[9,10],其将信息比特分割为两部分,一部分映射为一个码组,另一部分映射为码组中每个伪码的相位信息,此类方法也可提升信息传输率。进一步,随着更高信息速率要求的提高,又出现了索引调制[11,12]技术,其将部分信息比特映射为特定的索引,并索引控制调制信息,此索引部分信息不会耗费额外的能量,从而提升系统的传输率和能量效率。正是由于索引调制所具备在频谱效率和能量效率方面的独特优势,其已经受到越来越多的关注。目前的索引调制技术主要分为3类,即空间索引调制、子载波索引调制[13]和码索引调制[14,15]。直扩通信中有效的索引调制为码索引调制,其是将原本用来扩展频谱的伪码序列作为一种索引资源,即发射端的信息比特首先分割为两个部分,一部分信息比特通过调制符号进行传输,另一部分信息比特通过映射为伪码索引(编号)进行传输。基于码索引调制技术,又相继出现了码索引调制的扩展性研究[16],以及索引调制-差分混沌键控方案[17,18]。后续又出现了非正交码索引调制方法[19]、广义空码联合的索引调制方法[20],第1种方法是将信息比特分割为伪码映射块和调制信息块,并分别映射为伪码索引和调制符号,调制符号的实部与虚部再选择相同的激活伪码进行扩频;第2种方法是将索引的维度从1维增加到2维,增加2维信息的传输比特,此类方法可以提升系统误比特率性能、降低能量消耗,然而受复杂度问题的限制,信息传输率很难有大幅度提升。
可见,目前多进制扩频和索引调制的系列技术都是在传统(1维信息)基础上,附加传输映射信息,映射信息传输率与1维信息传输率的比值,即调制阶数决定了系统性能的提高。虽然目前方法可以改善信息传输率,但由于映射信息都是通过伪码的变换来映射的,因此调制阶数越大,伪码资源也越大,相关通道也就越多,造成的系统复杂度也就越大。当系统所承受的复杂度受限时,调制阶数也就无法提升,目前方法的调制阶数通常不超过5,极限时也很难达到10,为此目前的索引调制技术面临着高阶信息传输率提升无法突破的问题。
然而,随着通信需求和业务量的不断提升,直扩通信可能需要传输更多量级的指令,或者需要传输多级别、多应用的数据,因此,低复杂度的高阶索引调制方法研究尤为关键。为此,应对大数据量信息传输需求,为解决高阶信息传输率受限问题,本文提出一种低复杂度的超高阶码索引调制(UltraHigh Order Code Index Modulation, UHO-CIM)方法。
2 超高阶码索引调制




考虑信号传输过程中,环境因素可能会引发峰值偏移,而且对于所有通道的偏移影响应相近似,并结合式(14)中第3组伪码不存在3维信息的索引偏移,因此,利用ρi进行偏移差值计算,从而消除环境因素对峰值偏移的影响。

3 验证与分析
3.1 适应性分析


图1 峰均比结果
进一步,设2维调制阶数k为6,3维调制阶数µ为20,在3个码集C 1, C2和C 3中接收概率测试结果如图2所示。可见,UHO-CIM方法3个码集的接收概率都相差不明显,而且可以获得较高的接收概率,进而经统计分析,在其他参数条件下可以得到相同结论。

图2 接收概率结果
3.2 误比特率分析
目前较为有效的方法为CIM和M-ary方法,因此,对UHO-CIM方法与CIM和M-ary方法进行误比特率对比分析。当总调制阶数λ为5时的误比特率如图3所示。

图3 λ=5时的误比特率对比结果
可见,随着信噪比的增大,3种方法的误比特率都呈降低趋势,即性能越来越好。对于1维信息误比特率而言,由于UHO-CIM方法进行了修正处理,其误比特率略低于M-ary和CIM方法,表明UHO-CIM方法略改善了1维信息的误码性能。对于总体信息误比特率而言,由于M-ary方法的信息传输速率能力较低,而且复杂度较大,进而换取了一定的误比特率,因此M-ary方法的总体误比特率略低于UHO-CIM, CIM方法;而UHO-CIM方法与CIM方法的总体误比特率较近似,虽然略高于M-ary方法,但也能满足较低的误比特率要求。
当总调制阶数λ为10时,误比特率结果如图4所示,可见,随着总调制阶数λ的增大,3种方法的1维信息误比特率未出现明显差异,仍然是UHO-CIM方法略低于M-ary和CIM方法。而对于总体误比特率而言,随着调制阶数λ的增大,由于UHO-CIM方法中存在2维和3维处理机制,因此其总体误比特率也略呈降低趋势,而且逐渐略低于CIM方法,接近M-ary方法。经统计测试表明,当总调制阶数λ较小时,UHO-CIM方法的1维误比特率最低,性能最好,总体误比特率略高于M-ary方法,与CIM方法接近;当总调制阶数λ>10时,UHO-CIM方法的1维误比特率仍最低,性能最好,而总体误比特率则有所改善,略低于CIM方法,与M-ary方法接近,因此,UHO-CIM方法在高阶和超高阶的调制阶数时,误比特率性能呈现明显优势。
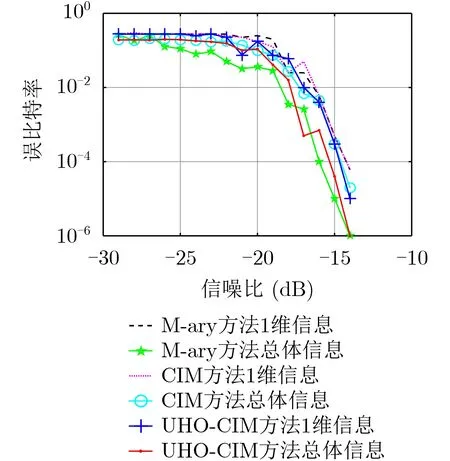
图4 λ=10时的误比特率对比结果
3.3 复杂度及综合性能分析
由于相关处理通道数量是影响复杂度的决定性因素,为此,以相关处理通道数量来建立复杂度衡量指标。当系统所需要的总调制阶数λ一定时,M-ary方法复杂度为式(32),CIM方法复杂度为式(33),而UHO-CIM方法中结合式(3)可得到阶数k=λ-µ,进而结合式(5)和式(6)可以得到k1,k2和k3,从而得到UHO-CIM方法复杂度为式(34)。

在不同的接收积累量情况下,当总调制阶数λ为低阶时,3种方法的复杂度对比结果如图5所示,可见,随着总调制阶数λ的增大,3种方法的复杂度都呈现增大趋势,而积累量对M-ary和CIM方法的复杂度未有明显影响;相同λ情况下,M-ary方法的复杂度最大,CIM方法优于M-ary,而UHO-CIM方法复杂度最低,则表明性能最优。当总调制阶数λ为高阶情况下,复杂度对比结果如图6所示,可见,当总调制阶数λ为高阶时M-ary方法的复杂度巨大,虽然CIM方法复杂度明显较低,但是通过局部放大后的结果可见CIM方法还是远远高于UHOCIM方法的复杂度,而且积累量越大则UHO-CIM复杂度越低,优势越明显。综上,经统计分析表明,M-ary方法和CIM方法的复杂度都与总调制阶数λ存在直接关系,而UHO-CIM方法的复杂度受k1,k2和k3影响,而k1,k2和k3是通过λ,µ计算得到的,数值远远小于λ,因此UHO-CIM方法的复杂度最低,而且积累量越大,则k1,k2和k3越小,因此复杂度性能也就越好。

图5 λ为低阶时复杂度对比结果

图6 λ为高阶时复杂度对比结果
进一步,考虑索引调制类方法都是一方面获得了速率的提高,一方面付出了相关处理复杂度的代价,为此建立综合性能指标来衡量获得速率提高阶数λ+1与付出复杂度ξ的比值(Performance and Complexity Ratio, PCR)如式(35)所示,从而评价方法的总体性价比。PCR越大则综合性能越好,当PCR为1时为评判门限,此时表明获得优势与付出代价相等价,综合性能没有提升也没有降低。

在不同的积累量情况下,当总调制阶数λ为低阶情况下,3种方法的综合性能PCR对比结果如图7所示,可见,随着总调制阶数λ的增大,CIM方法和M-ary方法的PCR一直都呈现降低趋势,而且都小于1,综合性能较差;而随着总调制阶数λ的增大,UHO-CIM方法则呈现增大趋势,而且远远大于1,综合性能非常优越。相同总调制阶数λ时,M-ary方法的PCR最低,CIM方法优于M-ary方法,而UHO-CIM方法的PCR远远高于其他两种方法,综合性能最好,此仿真结果符合式(35)推导,由于UHO-CIM方法的复杂度远远低于CIM方法和M-ary方法,因此,综合性能PCR远远高于CIM方法和M-ary方法。
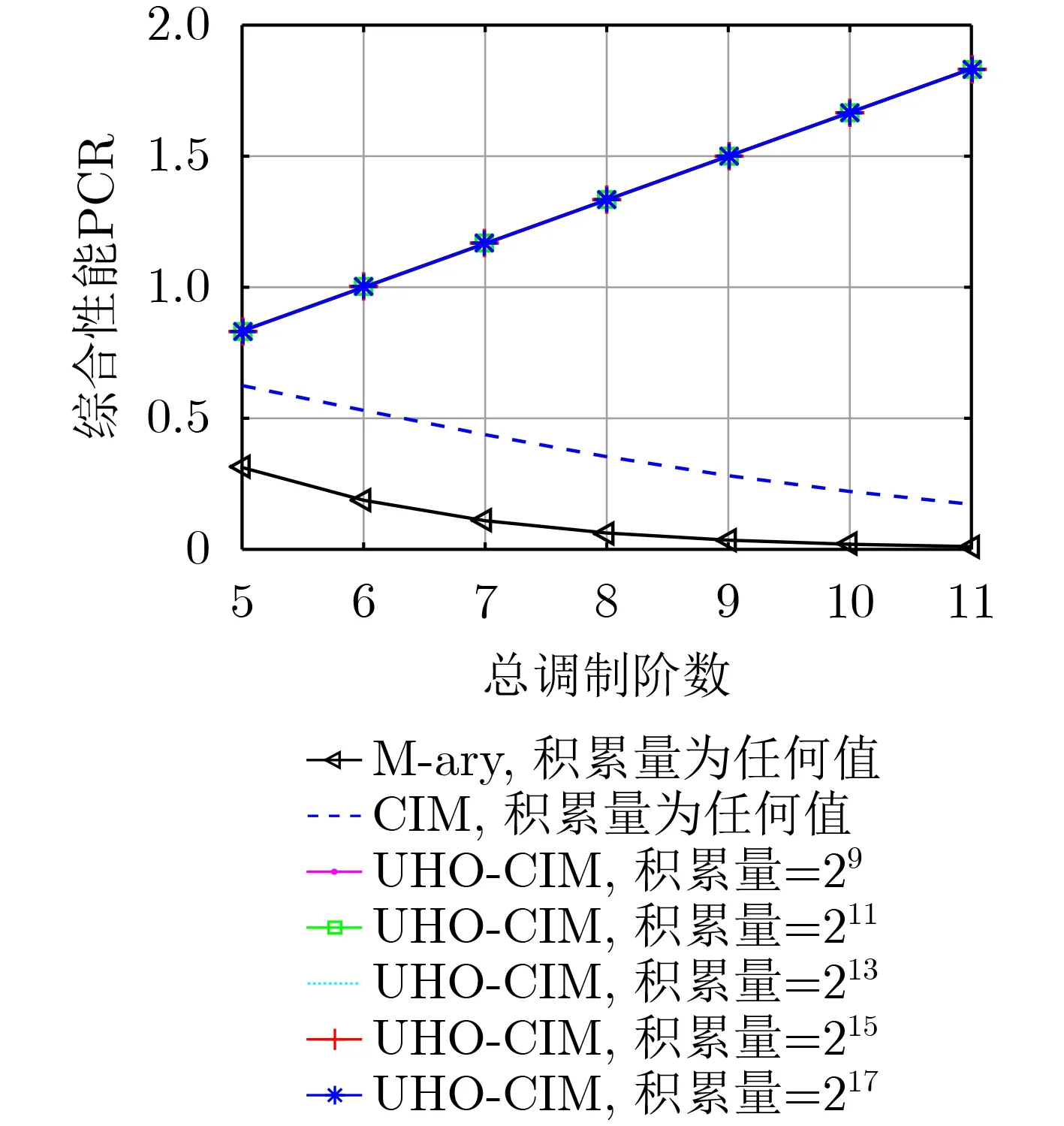
图7 λ为低阶时的PCR对比结果
进一步,当总调制阶数λ为高阶时,综合性能PCR对比结果如图8所示,可见,当总调制阶数λ在高阶范围时,随着λ的增大,CIM和M-ary方法的PCR一直都呈现降低趋势,而且远远小于1,综合性能较差。
而且,图8所示UHO-CIM方法在λ为高阶时开始出现拐点,积累量越大则出现拐点的调制阶数越大,性能也越好,虽然UHO-CIM方法在λ为超高阶范围时呈现降低趋势,但是其PCR仍然远远高于其他两种方法,而且也远远高于1,综合性能优势较明显。由此表明,UHO-CIM方法的综合性能PCR最高,而且积累量越大PCR性能越好,虽然λ在超高阶条件下,UHO-CIM方法的PCR呈降低趋势,但仍然高于1,也远优于其他方法,综合性能较好。

图8 λ为高阶时的PCR对比结果
最后,考虑通信系统能承受的复杂度不可能无限大,为此,当系统承受复杂度受限时,进行3种方法能达到的总调制阶数λ性能分析,对比结果如图9所示,可见,系统能接受的复杂度越大则3种方法能达到的总调制阶数λ也越大,信息传输率也就越大,但是增大趋势较缓;在相同复杂度情况下,UHO-CIM方法能达到的总调制阶数λ最大,CIM方法次之,M-ary方法最低;而且相关器积累量越大,UHO-CIM方法能达到的总调制阶数λ也越大。因此,在复杂度受限时,M-ary方法很难达到总调制阶数λ>10, CIM方法很难达到总调制阶数λ>15,而UHO-CIM方法则可以实现超高阶的速率传输。

图9 复杂度受限时能达到的总调制阶数
进而,当复杂度受限时,3种方法的综合性能PCR性能如图10所示,可见,相同复杂度情况下,M-ary方法的PCR最低,CIM方法略优于M-ary方法,而UHO-CIM方法远远高于其他两种方法,综合性能最优,而且相关器积累量越大,综合性能优势越大。随着系统能接受的复杂度的增大,3种方法PCR逐渐降低,其中M-ary方法和CIM方法都远远小于1,综合性能较差;而UHO-CIM方法在复杂度<40时,PCR都能满足>1,综合性能较好,当复杂度>40时,PCR开始<1,综合性能开始出现劣势,但是也远远高于其他两种方法。因此,当复杂度受限时,M-ary, CIM方法的综合性能很低,付出的代价远远超出了获得的速率提高,应用价值很低;而UHO-CIM方法综合性能较高,获得的速率提高能够远超付出的代价,应用价值较高。

图10 复杂度受限时PCR性能
4 结束语
为解决高阶信息传输率受限问题,本文提出一种高性能的超高阶码索引调制(UHO-CIM) 方法,以相对低的复杂度来达到超高阶调制阶数的信息传输。UHO-CIM方法在不低于–17 dB条件下都能够高效地实现信息传输;与现有的M-ary和CIM方法相比较,UHO-CIM方法的误比特性能最好,尤其在高阶和超高阶的调制阶数情况下,误比特性能优势更为明显;而且UHO-CIM方法的通道复杂度最低、综合性能最高,相关器积累量越大通道复杂度及综合性能优势就越明显;相对而言,M-ary方法很难达到总调制阶数>10, CIM方法很难达到总调制阶数>15,而UHO-CIM方法则可以实现超高阶的速率传输。因此,综合角度考虑,本文所提UHOCIM方法实现了高性能信息传输,可以为高效扩频通信应用提供可借鉴技术。
