基于高斯拟合与切比雪夫不等式的标签数量二次估计算法

严军荣 叶仁杰 钟 华 姜显扬

(杭州电子科技大学通信工程学院 杭州 310018)

1 引言

射频识别技术(Radio Frequency Identification,RFID)是一种通过阅读器在短时间内快速识别标签的非接触性识别技术[1]，当多个标签处于同一个阅读器的工作范围时，多个标签的应答信号会相互干扰导致阅读器无法正常读取标签内信息，这称为标签碰撞[2]。标签防碰撞问题是RFID系统中多标签识别的关键问题[3]。RFID系统中最常使用的防碰撞算法是ALOHA算法[4]，基于ALOHA的算法包括时隙ALOHA(Slotted Aloha, SA)算法[5]、帧时隙ALOHA(Frame Slotted Aloha, FSA)算法[6]、动态帧时隙ALOHA(Dynamic Frame Slot Aloha, DFSA)算法[7]以及其他改进算法[8,9]。

DFSA算法是目前比较主流的防碰撞算法，已经被一些RFID标准(ISO 14443-3, ISO 18000-6C和EPC Class1 Gen2)采用[10]。DFSA 算法的性能主要从标签数量估计和帧长度设定两个维度进行分析。文献[11]证明当帧长等于RFID系统中待识别标签的数量时，RFID系统达到最高吞吐率。准确地估算待识别标签的数量，尤其是在大规模应用场景下快速估算标签数量，是提高防碰撞算法性能的关键。

目前的标签数量估计算法主要分为两类，一类是基于系数的解析式估计算法[12–14]，另一类是根据目标函数进行最优值搜索的区间估计算法[15–17]。

文献[12]提出Low Bound估计算法，假定碰撞时隙中的平均标签量为2，文献[13]提出Schoute算法，假定碰撞时隙中的平均标签量为2.39。文献[14]证明当RFID系统中待识别标签数量是帧长3倍以上时，碰撞时隙内的平均标签数远多二者假定的标签量，因此Low Bound算法和Schoute算法在待识别标签数远大于帧长时估计误差相对较大。为此文献[14]提出一种基于分段解析式的标签数量估计算法，根据碰撞时隙比例的不同分段地调整平均标签数量的数值，该算法相对于Low Bound算法、Schoute算法能更好地适应标签数量的动态变化，但是分段处的跳跃间断点会导致估计值出现大波动，而且当碰撞时隙比例较大时不能及时调整碰撞因子值会导致大的估计误差。

文献[15]提出了基于切比雪夫不等式的区间估计算法，利用切比雪夫不等式进行标签估计。文献[16]提出了基于最大后验概率的区间估计算法，将估计区间内最大后验概率对应的标签量作为待识别标签数量的估计值。上述两种算法相对基于系数的解析式估计算法大幅提高了估计精度。但是算法分析复杂，且估计稳定性差。文献[17]提出基于粗精2次估计的RFID标签数目估计算法，该算法对待识别标签量进行粗精两次估计，在降低一定时间复杂度的同时提升了估计精度，但是增加了额外的时隙消耗；同时该算法在精估计时存在局部最优解的问题。

由上述分析可知，基于系数的解析式算法的性能取决于碰撞时隙中的平均标签数量，具有计算量小、估计精度低的特点；基于区间的估计算法在估计区间内逐一搜索寻找最优估计量，具有计算量大、估计精度高的特点。因此本文将上述两类算法的优点进行结合，提出一种基于高斯拟合与切比雪夫不等式的标签数量2次估计算法(Twice Labels Number Estimation algorithm based on Gaussian fitting and Chebyshev inequality, TLNEGC)。

2 TLNEGC算法

TLNEGC算法首先根据碰撞因子与碰撞时隙比例的关系建立碰撞模型，采用高斯函数对碰撞模型中的离散数据点进行拟合逼近获得高斯估计模型；然后利用高斯估计模型初次估计标签的数量，根据初次估计的结果判断是否需要进行2次估计，2次估计是利用切比雪夫不等式对估计区间进行2次搜索以获得最佳估计值。

2.1 高斯拟合模型

文献[9]证明了碰撞时隙的比例、碰撞因子之间的关系不受帧长影响。为获得碰撞时隙比例F与碰撞因子B的关系，参照文献[14]采用蒙特卡罗方法[18]对阅读器的读取过程进行模拟。

模拟中的参数设置如下：初始帧长取值128,256, 512，标签数量范围设置为[100, 1000]，实验次数为3000次。

仿真结果如图1所示。其中横轴是碰撞时隙比例F，纵轴是碰撞因子B。

图1中的蒙特卡罗数据点集分布满足高斯分布在X负半轴的分布特征，因此采用1维高斯函数对图1中的蒙特卡罗数据点集 (Bi,Fi), i＝1, 2, 3, ···,3000进行拟合。拟合形式如式(1)所示

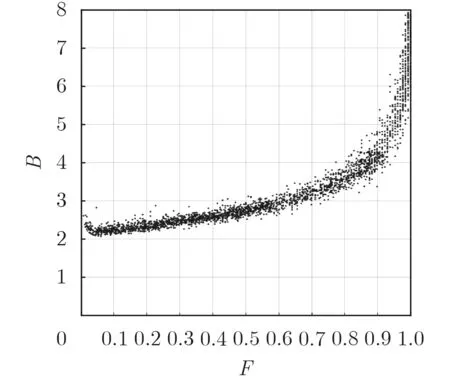
图1 碰撞时隙比例与碰撞因子之间的关系

根据高斯函数对图1进行拟合得到的高斯拟合曲线如图2所示。从图2可以看出式(6)给出的拟合曲线具有很好的拟合度。

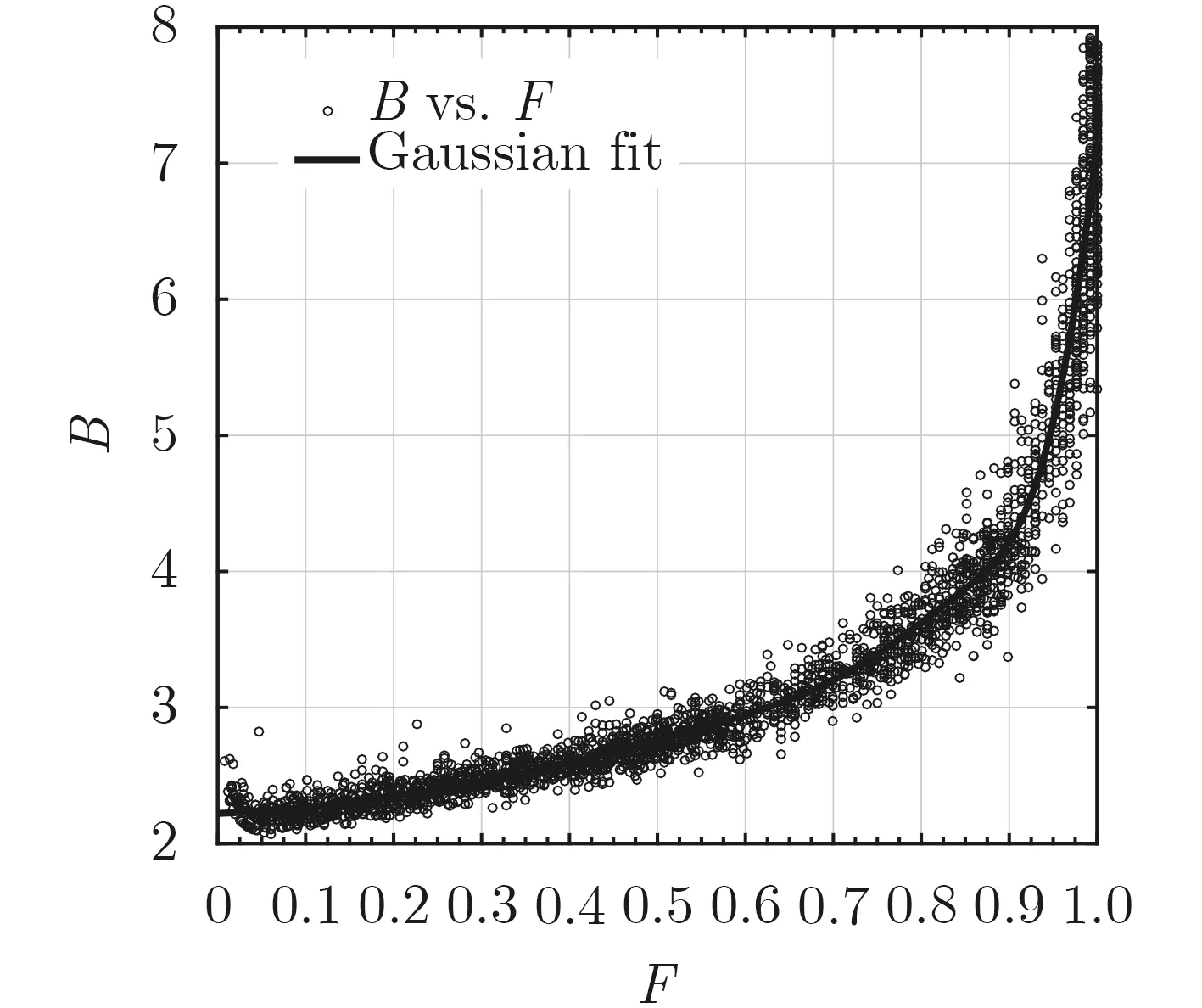
图2 高斯拟合曲线

2.2 初次估计解析方程

根据式(6)的拟合曲线，阅读器在一次读取后根据反馈信息获取B的值，从而估计出标签数量Ne(此时为初次估计值)可由式(7)所示

其中，C为碰撞时隙数，S为成功时隙数。

当初次估计值Ne小于帧长L时，帧长大于实际标签量，由多项分布可知，此时碰撞时隙数较少，成功时隙数较多，此时式(7)给出的解析式具有非常好的拟合度的估计精度，可直接将估计值输出为最佳估计值。当初次估计值Ne大于帧长L时，帧长小于实际标签量，由多项分布可知，此时碰撞时隙数较多，成功时隙数较少，Ne的精确度很大程度受到B的影响，那么需要对Ne进行2次估计。

2.3 2次估计

标签在响应阅读器的过程中随机选择一个时隙应答，根据数理统计知识可知，r张标签选择同一时隙的概率应满足多项分布。空闲时隙概率Pe、成功时隙概率Ps、碰撞时隙概率Pc可通过式(8)所示的公式计算得到。

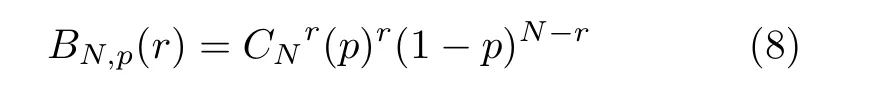
其中，P＝1/L，N为待识别标签数量。r＝0表示空闲时隙，r＝1表示成功时隙，r ＞1表示碰撞时隙。阅读器对标签的每一帧读取过程是独立的多次实验(每一帧的每一时隙为一次独立实验，每次实验的结果为空闲时隙、成功时隙、碰撞时隙的一种)，此碰撞场景适用于采用切比雪夫不等式进行估计。

利用切比雪夫不等式对Ne的初次估计结果进行估计，该方法的基础是随机试验的结果应接近于期望值。为此，设定的一个估计区间Δ，在Δ内计算每一个标签量n对应的每个时隙的期望，计算每个时隙期望与实际值之间的切比雪夫距离D，在Δ内搜索出一个标签量n使得切比雪夫距离D最小，该标签量n即最佳估计值。切比雪夫距离D由式(9)所示

2.4 TLNEGC算法流程

TLNEGC的算法流程如表1所示。

表1 TLNEGC的算法流程

3 算法仿真与分析

使用Matlab软件进行仿真实验，从估计误差、时间复杂度、总时隙数消耗、总时间消耗、稳定性5个角度进行对比。

3.1 估计误差

设ε为估计误差率，Ne为标签数量的估计量，N为RFID系统中实际存在的标签数量，那么ε可由式(10)计算

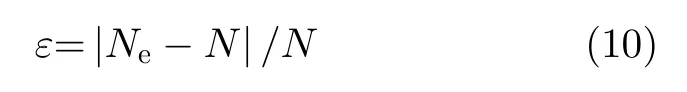
对本文提出的TLNEGC算法和现有的Low Bound算法、Schoute算法、最大后验概率算法、粗精2次估计算法的标签数量估计误差率进行仿真，仿真结果如图3所示。图3中的横坐标为标签数量，取值范围为[100, 1000]，纵坐标为估计误差率。

由图3可知，TLNEGC算法误差曲线整体平缓，误差均值为2.2%，最大估计误差不超过4%。Low Bound算法、Schoute算法、算法的估计误差率随着标签数量的增多迅速上升。最大后验概率算法的估计误差比Low Bound算法、Schoute算法更低，但明显高于TLNEGC算法而且误差曲线起伏大。粗精2次估计算法在估计精度、估计稳定性方面优于Low Bound算法、Schoute算法、最大后验概率算法，但估计误差仍然高于TLNEGC算法。

图3 误差对比

由此可知，TLNEGC算法相比现有算法的估计误差更低、稳定性更好。其原因在于TLNEGC算法采用了2次估算，第1次是动态调整解析式系数以降低估计误差，第2次是利用切比雪夫不等式对初次估计的结果进行2次搜索以提高估算精度。

3.2 时间复杂度

使用算法的运行时间来衡量时间复杂度。对本文提出的TLNEGC算法和现有的Low Bound算法、Schoute算法、最大后验概率算法、粗精2次估计算法的运行时间进行仿真，仿真结果如图4所示。图4中的横坐标为标签数量，取值范围为[100,1000]，纵坐标为运行时间。

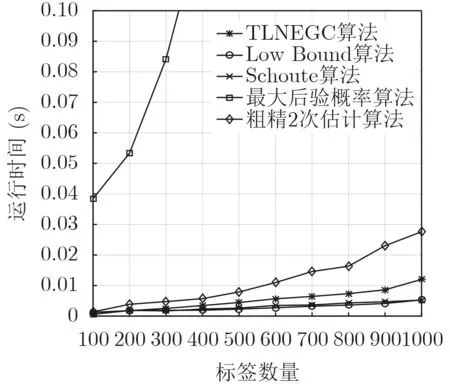
图4 运行时间对比

由图4可知，本文提出的TLNEGC算法的运行时间与标签量的增长呈正相关，平均运行时间为0.0054 s；时间复杂度为O(n)。Low Bound算法、Schoute算法的运行时间与标签数量的增长基本无关，时间复杂度为O(1)，平均运行时间为0.0029 s。最大后验概率算法的运行时间随着标签的增加呈指数增长，算法的时间复杂度为O(n2)，平均运行时间为0.346 s。粗精2次估计算法的运算时间与标签量的增长呈正相关，时间复杂度也为O(n)，平均运行时间为0.012 s。

由此可知，TLNEGC算法的运行时间略长于系数类估计算法，但是明显低于其他高精度区间类估计算法。其原因在于TLNEGC估计算法在初次估计时只做1次乘法，在利用切比雪夫不等式进行2次估计时也只做0.12n次乘法，因此总体时间复杂度仍能保持在O(n)。

3.3 总时隙数消耗

为了验证TLNEGC算法的识别效率，以识别全部标签所需的总时隙数消耗为衡量指标，对本文提出的TLNEGC算法和现有的Low Bound算法、Schoute算法、最大后验概率算法、粗精2次估计算法的运行时间进行仿真，仿真结果如图5所示。图5中的横坐标为标签数量，取值范围为[50, 250]，纵坐标为识别所需总时隙数。

由图5可知，TLNEGC算法的总时隙数消耗曲线平直，平均消耗414个时隙就能完成识别。Low Bound算法的总时隙数消耗曲线起伏较大，平均消耗602个时隙就能完成识别。Schoute算法的总时隙数消耗曲线同样起伏较大，平均消耗564个时隙能完成识别。最大后验概率算法总时隙消耗曲线平缓，平均消耗458个时隙能完成识别。粗精2次估计算法总时隙消耗曲线总体平缓，平均消耗834个时隙完成识别。

图5 完成识别所需总时隙数消耗比较

由此可知TLNEGC算法相比现有算法的总时隙数消耗更少。这是由于TLNEGC算法估计精度高，有效地减少了时隙消耗。

3.4 总时间消耗

为了分析TLNEGC算法的总时间消耗，以识别全部标签所需的总时间消耗为衡量指标，对本文提出的TLNEGC算法和现有的Low Bound算法、Schoute算法、最大后验概率算法、粗精2次估计算法的运行时间进行仿真，仿真结果如图6所示。图6中的横坐标为标签数量，取值范围为[100, 500]，纵坐标为识别所需总时间。

图6 完成识别所需总时间消耗比较

由图6可知，TLNEGC算法的总时间隙数消耗曲线平直，平均消耗0.43s就能完成识别。Low Bound算法的总时间隙数消耗曲线较为平直，平均消耗0.56 s完成识别。Schoute算法的总时间隙数消耗曲线同样较为平直，平均消耗0.73 s完成识别。最大后验概率算法的总时间消耗曲线陡峭，平均消耗0.78 s能完成识别。粗精2次估计算法的总时间隙数消耗曲线较为平直，平均消耗0.94 s完成识别。

由此可知TLNEGC算法相比现有算法的总时间消耗更低。这是由于TLNEGC算法有较高的估计精度，有效地减少估计时隙消耗。同时TLNEGC算法运行时间短，减少了估计时间的消耗。

3.5 稳定性

由于存在捕获效应，部分碰撞时隙会被阅读器识别为成功时隙，会引起标签的丢失，导致碰撞时隙和成功时隙与实际情况不符。本节对捕获效应下算法的估计结果进行仿真对比，其中捕获效应发生的概率设置为0.15。

对捕获效应下TLNEGC算法和现有的Low Bound算法、Schoute算法、最大后验概率算法、粗精2次估计算法的标签数量估计误差率进行仿真，仿真结果如图7所示。图7中的横坐标为标签数量，取值范围为[100, 1000]，纵坐标为估计误差率。

图7 捕获效应下的估计误差

计算估计误差的均方差。TLNEGC算法的均方差为0.0086。Low Bound算法、Schoute算法的均方差分别是0.2376, 0.2304。最大后验概率算法的均方差为0.1550。粗精二次估计算法的均方差为0.0174。

由此可知在捕获效应的场景下，TLNEGC算法估计误差的均方差低于现有估计算法，稳定性更好。其原因在于TLNEGC算法在第1次估算时动态调整解析式系数以降低估计误差，在第2次估算时利用切比雪夫不等式对初次估计的结果进行2次搜索保证了估计的稳定性。

4 结论

针对RFID系统中标签数量估计算法存在的估计精度不高、识别时延长、时间复杂度高的问题，本文提出一种基于高斯拟合与切比雪夫不等式的标签数量二次估计算法TLNEGC。仿真结果表明，TLNEGC算法在大规模标签场景下的平均估计误差为2.2%，平均消耗414个时隙完成标签数量识别，完成识别平均时间消耗0.43 s，明显优于现有标签数量估计算法且具有较高的稳定性。本文所提TLNEGC算法具有估计精度高、时间复杂度低的优点，对于标签数量识别具有一定的应用价值。