单星多波束天线下基于压缩感知的多目标干扰定位

张 轶 翟盛华 陶海红

①(中国空间技术研究院西安分院 西安 710100)

②(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

随着在轨卫星数量的不断增多及卫星频谱资源越来越紧张，干扰问题日益突出，严重影响卫星通信网络正常稳定运行。为了减小和消除干扰造成的恶劣影响，通常需要采用卫星干扰源定位技术[1,2]。单星定位系统仅利用1颗观测卫星实施干扰定位，可摆脱双星定位中对邻星和卫星星历等遴选条件的限制[3,4]。

常用的单星定位体制有：(1)单星仅测向：利用相位干涉仪或空间谱估计算法对来波方向进行估计。其中，干涉仪法的测向范围受基线长度限制，容易产生相位模糊；同时由于其设备复杂、造价高，目前常应用于侦查卫星中[5]。空间谱估计方法可实现高测向灵敏度和准确度，但对星载天线阵列有很高的要求[6]。(2)利用运动学原理：星上接收机在不同位置通过对同一干扰源测量得到的多个多普勒频率或脉冲到达时间进行定位[7]。该技术难以有效应对多目标问题，且对卫星姿态及同步要求很高，因此只适用于低轨卫星或倾斜轨道卫星。(3)幅度比较式测向：利用天线的方向特性，按照接收信号幅度的不同，测定不同来波方向。该体制实现相对简单，但定位精度过度依赖天线方向图的测量精度，且无法同时处理多个同频干扰[8]。

近年来，压缩感知(Compressive Sensing,CS)理论[9]的兴起为我们提供了一种全新的视角去看待多目标问题。研究表明，基于CS的多目标定位方法已在无线传感器网络(Wire Sensor Networks,WSN)中得到了广泛应用，并凸显出比传统方法更好的定位性能[10–12]。但是该方法需建立大量的无线链路以实现对定位区域的充分覆盖，而卫星多波束天线的覆盖特性恰好为二者的结合提供了基础。

鉴于此，本文针对多目标定位问题，提出一种将压缩感知理论应用于多波束卫星的干扰定位方法，给出了明确的系统模型和算法流程；推导了定位误差的理论值并分析了影响误差的主要因素；通过软件仿真，验证了所提方法具备较好的定位性能。

2 多目标定位模型

2.1 节点分布特性

空间网格化是构建多目标定位模型的基础。不失一般性，设已知存在K个目标干扰源的2维感知区域被离散成N个网格节点，M个卫星波束各自对应1个传感器，用以测量其覆盖范围内各节点处参考信号的接收信号强度(Received Signal Strength,RSS)。以圆形波束为例，其覆盖单元可用正六边形的蜂窝结构(等效边长为l)，且各图形之间不存在重叠或者空隙，图1所示为19个蜂窝网波束下的四色频分复用方式。

图 1 多波束四色复用示意图

其中，-∞＜t ＜∞, I和ω是相互独立的随机变量，且分别服从区间[0, R]和[0,2π]上的均匀分布。在空间网格点数目足够大的条件下，可以用节点坐标近似估计目标的位置来对K个干扰源进行定位。

2.2 压缩感知定位原理

由于K ≪N，所以干扰源的位置在空域上具有稀疏性。根据CS理论，多目标问题可以抽象成通过M维接收信号强度的有噪测量(卫星信道中近似为高斯白噪声)，重构出N维空间中K稀疏位置矢量的近似问题。基本模型为其中，P为信号发射功率，At为雨衰、大气吸收、电离层闪烁等引起的附加衰减，与实时链路状态相关。G表示波束增益，可近似计算为[13]

(5) 观测矢量y ∈RM×1：观测矢量为M个传感器的实际RSS测量结果。由于多波束天线具有高灵敏度，点波束旁瓣值较高，导致邻近波束之间有较大的重叠区域。当系统受到干扰时，除主要受干扰波束接收到干扰信号外，其邻近波束也会接收到该信号(即带外信号)。因此，y＝(y1,y2,···,yM)T中的任一元素yi代表第i个传感器感知到的所有目标的功率叠加结果。

2.3 算法流程

图2展示了基于CS的多目标定位方法总体框架结构，分为离线和在线两个阶段：

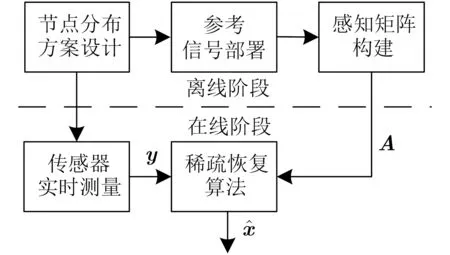
图2 总体框架结构

(1) 离线阶段

步骤 1 建立坐标系。以1号蜂窝单元中心为原点建立平面坐标系，并以此推算各波束中心指向坐标；

步骤 2 设计节点分布方案。按照2.1节方法在圆形覆盖区域内随机产生N个动态节点，并记录所有节点坐标；

步骤 3 构建感知矩阵。将参考信号置于各节点处，根据多波束天线方向图的分布特性，各点波束在不同信号源方向上的天线增益不同，使得所接收到的信号强度有较大的差异，因此按照式(3)计算各传感器处的RSS，具体实施为：归一化参考功率，则干扰功率等于功率系数k；入射角度、链路长度可结合三角函数关系，由各节点坐标、星地距离、地球曲率等联合计算得到；考虑到目标频率的随机性会形成感知矩阵的不唯一性，故将载波频率按照复用方式分别代入，对测量结果取平均值。

(2) 在线阶段

步骤 4 测量RSS。当系统检测到干扰时，对各传感器接收到的所有干扰信号进行观测，并统计功率叠加结果；

步骤 5 重构稀疏矢量。利用稀疏恢复算法(如正交匹配追踪(Orthogonal Matching Pursuit,OMP)、基追踪(Basis Pursuit, BP)、原对偶内点(Primal-Dual Interior Point, PDIP)算法等[14,15])求解目标干扰的位置矢量信息；

步骤 6 确定干扰位置。以通过门限判决的有效值对应的节点作为目标位置的近似估计，完成定位。

3 定位性能分析

3.1 随机分布误差

由于采用动态网格化的定位方法，故当定位成功时，估计误差ε可等效为任意两个相邻参考信号之间距离的期望。不妨设任意相邻节点的坐标为

其中，D(ε)为ε的方差。已知下列算式成立

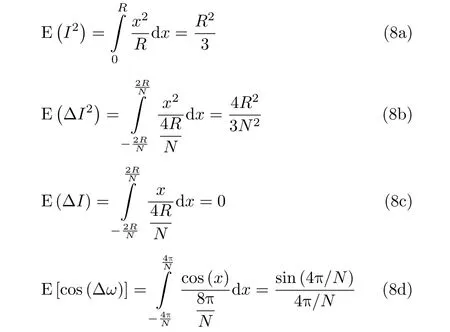
将式(8)代入式(7)可得

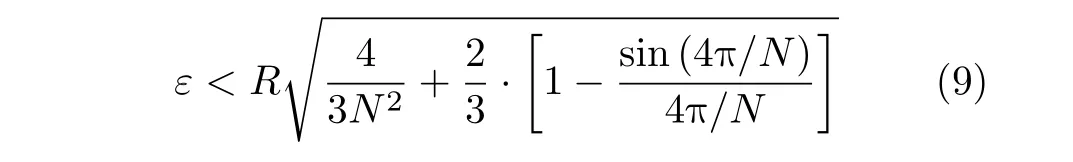
由于D(ε)随N增大而减小，因此N越大，ε越趋近于右边表达式。

3.2 稀疏重构算法的影响

考虑到重构算法对定位性能的影响，还需从以下因素进行分析：

(1) 节点数N：在多目标定位问题中，基于CS的方法将参数空间离散化以获得目标所在节点的近似估计，显然N越大，节点与目标之间的误差就越小，式(9)也佐证了这一点；但同时N过大会导致稀疏基矩阵中各元素间的相关性增强，影响算法性能。

(2) 干扰数K：从压缩重构的角度看，给定节点分布方案确定了A的构成，从而进一步确定了能够重构出的最大目标数K，换言之，传感器个数M需满足[16]

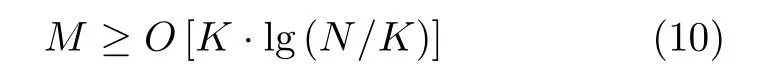
因此对于生成波束不变的卫星系统，K存在理论上限。

(3) 覆盖半径r：点波束覆盖半径越大，其与相邻波束之间的重叠区域就越大，不同传感器对同一干扰提供的信息就越多，但由于目标在感知区域内是稀疏分布的，故这个信息量是有限的；若波束间重叠区域很小，则各传感器近似独立工作，使信号重构效果变差。

(4) 判决门限T：通过对xˆ中 的非零元素设定阈值，以减小因噪声和算法误差引起的“扰动项”。需要注意的是，由于目标数量和发射功率是未知的，利用重构算法进行信息恢复时，可能将一处干扰的RSS识别为多个目标共同作用的结果，因此随着T增大，中可用信息的数量会减少，影响对定位结果的判断。

综上，给出下述评价指标作为衡量定位性能的依据：

定位成功率ρ：以估计位置为圆心，当实际目标处于任一搜索半径范围内视为定位成功，即能够被正确识别的干扰数所占的比例称为定位成功率。

定位误差δ：在定位成功前提下，满足搜索范围重叠区最小处的质心与实际目标的距离视为定位误差。

4 仿真实验

仿真参数配置如表1所示，其中频率设置的标准是3 dB波束宽度满足至少能覆盖1个蜂窝单元；循环迭代次数为500，每次执行时随机生成N个节点坐标和K个干扰坐标，同时随机分配频率和功率；不同仿真条件下只对相应参数作动态调整，其余不变；不考虑附加衰减影响，最后对统计结果进行仿真分析。

表1 仿真参数配置

4.1 计算干扰识别概率

图3为不同重构算法下干扰数识别概率的统计结果。通过计算干扰识别数的期望，可以得到在4目标随机分布条件下，OMP, BP和PDIP算法执行时成功定位的概率分别达到0.66, 0.70和0.73，充分验证了本文提出方法的可靠性，其中PDIP算法的性能相对最优；但针对上述重构算法的比较，并非本文研究重点，这里不再赘述。实际应用时可在条件允许情况下对RSS进行连续采样，从而利用多次观测降低随机误差对定位结果的影响。

图3 不同干扰数的识别概率

4.2 不同参数下的性能验证

采用PDIP算法，图4为不同节点数下定位成功率、定位误差随干扰数变化的仿真结果。从图中可以看到，定位性能随干扰个数的增大而显著下降，这是因为位置矢量的稀疏度随之增大，算法的信号重构能力下降。由式(10)可知，对于M ＝ 19和N ＝100～400的部署方案，K的理论上限分别为7, 5,4和4。图4(a)中，相同干扰数下N越大定位成功率越低，但当K分别取理论上限时各情形的ρ值相近；当K超过理论上限时，定位成功率均低于70%。图4(b)中，当K小于理论上限时，各情形的定位误差均满足式(9)，且相同干扰数下N越大定位误差越小；但是随着K增大，受限于式(10)所示约束条件，N为400时δ值的增长趋势甚至超过其他情形。上述仿真结论均与第3节相关理论一致，充分验证了分析的合理性。综上所述，当波束数(传感器数)固定时，节点数越大可获得更精确的估计结果，越小则能进行更多目标的定位，因此对N的选取应根据实际情况进行折衷考量。

图4 不同节点数下定位性能与干扰数仿真结果

图5为不同覆盖半径下定位成功率、定位误差随判决门限变化的仿真结果。从图中可以看到，相同判决门限下，定位性能随覆盖半径增大而显著上升，这是因为各传感器之间协作程度随之增大，提高了信号重构的准确度；但当r ≥3l时存在一个相对稳定的上界，这是由目标的K-稀疏分布决定的。图5(a)中，定位成功率随判决门限增大而缓慢下降，但在r ≥2l的情形中均保持在60%以上。图5(b)中，定位误差不随判决门限的变化而显著改变；当r ＝ l时，δ值在15 km上下波动，已经大于式(9)给出的理论上限，说明此时定位模型几近失效，根据误差定义，仿真曲线反映的即是搜索半径值的平均统计特性。上述仿真结论均与第3节相关理论一致，充分验证了分析的合理性。综上所述，判决门限对定位性能的影响有限，而波束覆盖半径的大小则是实现压缩感知多目标定位的关键因素。

图5 不同覆盖半径下定位性能与判决门限仿真结果

根据仿真结论将各评价指标与关键参数的大致对应关系汇总如下(见表2)。其中，“+”表示成正比，“–”表示成反比，“/”表示无直接关系。

表2 评价指标与关键参数对应关系

4.3 与其他卫星定位方法的比较

将本文方法与相位干涉仪、空间谱估计(又称波达方向(Direction Of Arrival, DOA)估计)测向方法进行性能比较。针对传统干涉仪只适用于单目标情形，考虑利用旋转干涉仪(Rotating Interferometer, RI)处理多目标问题，即通过对干涉仪在不同旋转角度下的采样数据进行预处理，构造虚拟阵列数据对多目标参数进行估计；DOA估计中采用经典的MUSIC(MUltiple SIgnal Classification)算法，接收端考虑19馈源的3层环阵排布方式。由于RI和DOA均为针对来波角度参量(俯仰角、方位角)的估计方法，为便于比较，需要对测向结果进行转换。

假设确定干扰坐标的随机变量为I和ω，测向时俯仰角、方位角误差分别为α和β，则估计坐标的参量可表示为

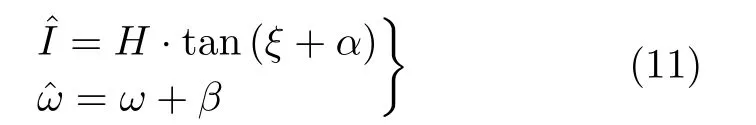
其中，tan(ξ)＝I/H, H表示星地距离，这里取值为36000 km。利用式(11)得到的坐标可计算求解定位误差。此外，为更直观地描述低信噪比下的定位性能，本例中将搜索半径设置为500 km。

图6为不同定位方法下定位误差随信噪比(Signalto-Noise Ratio, SNR)变化的仿真结果。可以看到，随着信噪比的增大，目标参数的定位误差逐渐减小，3种方法在SNR ＝ 20 dB时的定位精度分别达到30.2 km, 18.9 km和7.7 km；其中本文方法的定位性能相对最优，且在低信噪比段(0～5 dB)仍具备较强的竞争力。具体原因是RI和DOA法利用阵元测量相位差时，受通信卫星轨道高度的影响，其基线长度难以保证有效的测量精度；DOA法测向时还利用了信号的幅度参数，因此其定位性能优于RI法；而所提方法基于“同一地理区域信号在同一时间帧中具有功率变化的正相关”这一特征，在构造感知矩阵时能够最大化减少低信噪比的影响，只是在信号重构时会引入与噪声相关的“扰动项”，但当SNR ＞ 5 dB时误差曲线趋于平缓，定位精度较高。

图6 不同定位方法下定位误差与信噪比仿真结果

5 结束语

本文提出将压缩感知相关理论应用于多波束卫星的干扰定位场景中，旨在解决空分频率复用下多个干扰目标位置的识别问题。该方法利用星载多波束天线的方向特性，通过动态节点化参考信号，只需测量接收信号强度及求解一个稀疏恢复问题，便可重构出包含多个目标位置信息的稀疏矢量。研究结果表明，定位性能与节点分布、干扰个数、波束覆盖半径、判决门限等诸多因素有关；在一定参数条件下，该方法在定位成功率及定位误差方面均能取得较好的定位效果，且其定位精度明显优于相位干涉仪和空间谱估计方法，因此对卫星干扰定位技术应用具有一定的参考价值。在此基础上，之后的研究工作可结合坐标系转换、链路衰减适配等方面深入展开，以进一步简化模型参数、提高定位性能。