一种谐振倍压电路型串联超级电容电压均衡器

杨晓光，刘介桃，齐亚康，陈玫琪

(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学河北省电磁场与电器可靠性重点实验室，天津 300130)

超级电容作为一种新兴的储能器件，在储能系统中得到了广泛应用。由于超级电容单体额定电压较低，为了满足电压和储能容量的需求，需要将多个超级电容单体串联使用[1]。然而，由于单体超级电容在容量、内阻和自放电率等方面存在差异，实际应用中会造成单体超级电容之间的电压逐渐趋于不平衡。电压不平衡问题会引起某些超级电容的过充和过放现象[2]，使得系统容量不能得到充分利用，影响超级电容使用寿命，甚至造成火灾、爆炸等危险事故。

目前已经提出了多种电压均衡技术来解决电压不平衡的问题，相比于被动型均衡电路，主动型均衡电路的均衡速度快，均衡效率高，是一种更具有发展前景的解决方法。传统主动均衡技术主要采用双向DC/DC 变换器，电感或电容以及变压器作为能量交换的均衡方案。基于双向DC/DC 变换器的电压均衡器[3-4]需要大量的可控开关，也就需要对应数量的驱动电路，系统复杂性较大。基于变压器的均衡方案[5-6]具有较少的变换器和可以自动直接对单元均衡的优点，但二次绕组间参数匹配要求严格，给设计带来困难，扩展性降低。文献[7-8]采用开关电容用于单元间均衡，这类均衡器具有良好的扩展性，但所需均衡器的数量与串联的单元数量成正比，增加了系统的复杂度和成本。由于多倍压电路仅由二极管和电容组成，因此基于多倍压电路的均衡器电路简单，可扩展性好。典型的多倍压电路为Cockcroft-Walton(CW)电路[9-10]，如图1(a)所示。另外一种改进型倍压均衡电路如图1(b)所示，此类均衡电路存在均衡电流叠加现象，因而电流纹波较大，并且均衡速度较慢，均衡器中的开关管采用硬开关方式[11-12]。

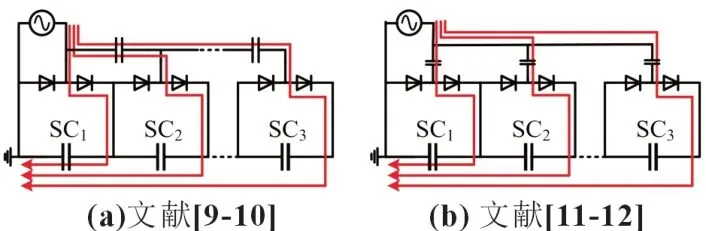
图1 基于多倍压电路的均衡器

针对上述问题，本文提出了一种基于谐振倍压电路的电压均衡器，此均衡器主要由半桥谐振变换器和对称式倍压电路组成。半桥谐振变换器驱动控制简单并且实现了软开关；对称式倍压电路均衡速度快，无电流叠加问题，二极管实现了软开关，无反向恢复问题。

1 均衡器的结构

本文所提出的均衡器拓扑如图2 所示，主要由半桥谐振变换器和对称式倍压电路组成。QH和QL组成半桥，Lr为谐振电感，Cr为谐振电容，T 为变压器，Lr和Cr在QL两端的方波电压的驱动下进行谐振。变压器的副边接对称式倍压电路，C1a-Cna和C1b-Cnb为耦合电容，D1a-D1d…Dna-Dnd为二极管，SC1-SCn为储能系统的串联超级电容。串联超级电容SC1-SCn经半桥谐振变换器与对称式倍压电路优先将能量传递给SC1-SCn中电压最低的超级电容，从而实现将SC1-SCn的电压VSC1-VSCn均衡一致。

图2 基于半桥谐振变换器和对称式倍压电路的电压均衡器

2 稳态分析

2.1 工作原理

由于超级电容容量大，并且均衡器工作频率高，因而在一个开关周期内将超级电容等效成一个恒压源，假定对称式倍压电路中所有的二极管以及耦合电容完全一致。图3 给出了当SC1电压最低时，两种开关状态分别对应的工作模态图。电路的关键波形如图4 所示，D为占空比，ts为开关周期。[t0～t3]时段，开关管QH导通，[t3～t6]时段，开关管QH关断，QL与QH互补导通。

图3 当SC1电压最低时对应的工作模态图

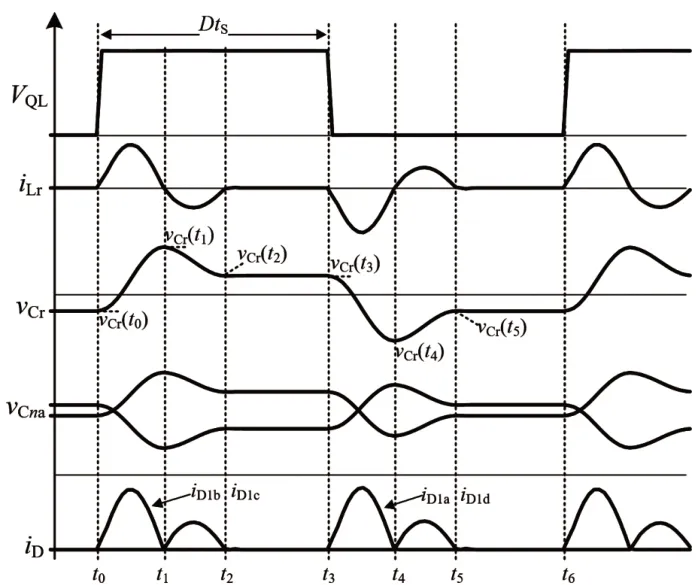
图4 关键波形图

[t0～t3]时段：QH导通，QL关断，串联的超级电容与Lr和Cr谐振腔以及变压器原边组成谐振回路，谐振电流经变压器传递至副边，变压器副边、耦合电容、二极管与电压最低的储能超级电容形成回路。[t0～t2]时段谐振电流不为零，变压器给后级传能。[t2～t3]时段谐振电流为零，Cr两端电压维持不变，变压器不传递能量。

在t0时刻，QH导通，串联的Lr和Cr两端承受高压，谐振开始，流过QH的电流从零值开始上升，电流上升速度受到Lr和Cr谐振腔限制，QH实现零电流开通。在t3时刻，QH关断时，谐振电流已经截止，流过QH的电流为零，因此QH为软关断。

[t3～t6]时段：QH关断，QL导通，Lr和Cr谐振腔以及变压器原边组成谐振回路，谐振电流经变压器映射至副边，变压器副边、耦合电容、二极管与电压最低的储能超级电容形成回路。这个时段是Lr和Cr谐振腔释放能量，[t3～t5]时段谐振电流不为零，变压器给后级传能。[t5～t6]时段谐振电流值为零，Cr两端电压维持不变，变压器不传递能量。

在t3时刻，QL导通，Cr两端电压不再维持不变，Cr中的能量开始释放，流过QL的电流从零值开始上升，电流上升速度受到Lr和Cr谐振腔限制，QL实现零电流开通。在t6时刻，QH关断时，谐振电流已经截止，流过QL的电流为零，因此QH为软关断。

由以上分析可知：所提出的均衡器工作谐振电流断续模式(如图4 中iLr所示)两个可控开关管都可以实现软开关，并且如图4 中iD所示，流过二极管的电流自然谐振到零，实现二极管软关断。

2.2 数学模型

为了简化均衡器的描述，引入谐振电路特性阻抗Z0、特征角频率ω0和谐振角频率ωr，定义如下：

式中：req为谐振回路的等效电阻，等于变压器一次侧电阻与从变压器二次侧映射到一次侧的等效电阻之和；tr为与ωr对应的谐振周期。

由于均衡电流和线路电阻都较小，则变压器原边电压Vp表示为：

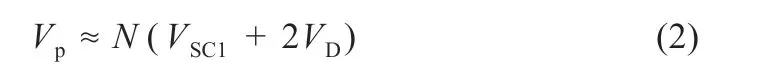
式中：Vp为从变压器二次侧映射到一次侧的电压；N是变压器变比；VD为二极管压降。

根据图3 中的谐振回路可以列写状态方程如下：

整个开关周期ts分为6 个工作模态，变换器主要工作波形如图4 所示，各个模态分析如下：

模态1 [t0≤t≤t1]：t0时刻开始，电流iLr开始增加，通过变压器映射到二次侧，并流过电压最低的超级电容SC1，谐振电流表达式和谐振电容电压在t1时刻值分别表示为：

模态2 [t1≤t≤t2]：t1时刻后iLr反相，变压器一次电压Vp极性反向。在此模态，谐振电流表达式和谐振电容电压在t2时刻值分别表示为：

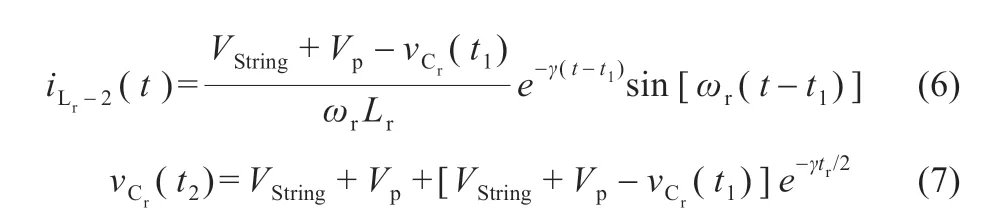
模态3 [t2≤t≤t3]：在t2时刻，iLr达到零值，并在此模态保持为零，且谐振电容的电压维持不变：

模态4 [t3≤t≤t4]：t3时刻QH关断，QL导通，此刻开始谐振电容电压不再维持不变，开始释放能量进行谐振，同理可以得出此模态谐振电感电流表达式和谐振电容电压在t4时刻值表达式，分别为：

模态5 [t4≤t≤t5]：t4时刻，谐振电流换向，在此模态谐振电流表达式和谐振电容电压在t5时刻值表达式分别为：

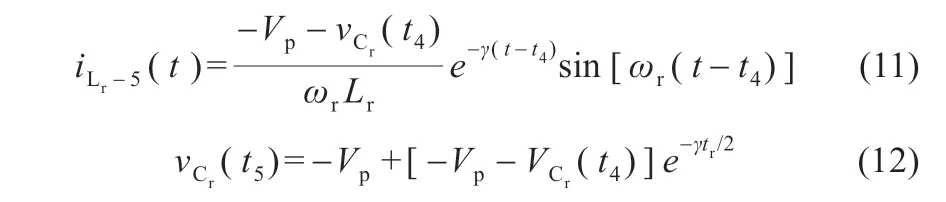
模态6 [t5≤t≤t6]：在t5时刻，iLr达到零，并在此模态保持为零，并且谐振电容的电压保持恒定，直到下一个周期开始，可得：

联立式(5)，(7)，(8)，(10)，(12)和(13)可解得谐振电容电压的各个时刻值如下：

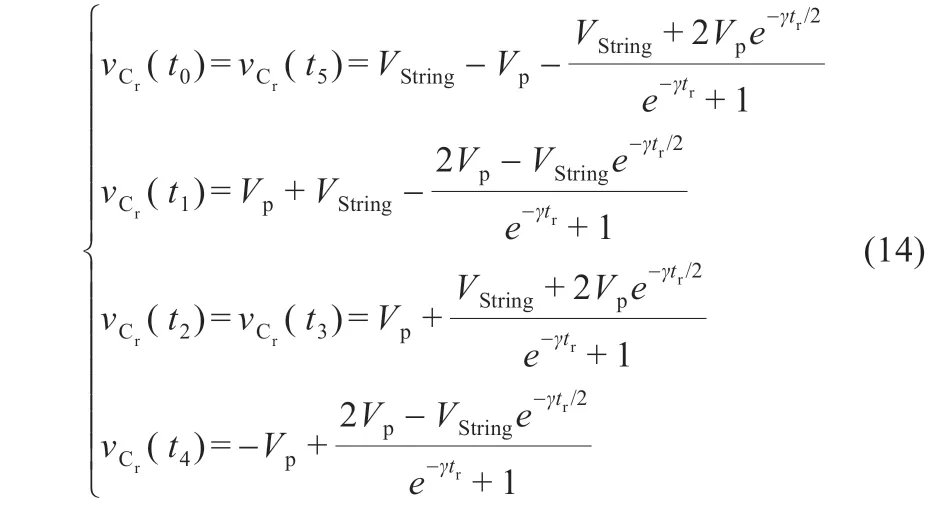
将式(14)分别代入式(4)，(6)，(9)和(11)可得到各个阶段的谐振电流的表达式：

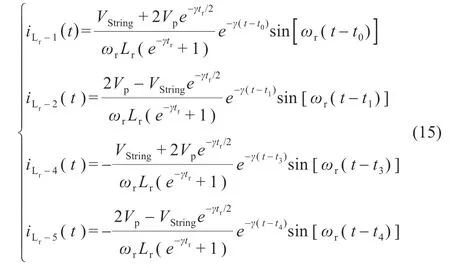
由式(15)，将各个阶段的谐振电流绝对值积分求和，并在一个开关周期ts时长内取平均，可得均衡电流平均值为：

当电路各个器件选定以后，γ，ω0和tr不变，VString和Vp在短时间内不会有明显变化，req很小可以忽略时，此时可以认为γtr趋近于零，因而式(16)可化简为：

式中：fSN为开关频率与谐振频率的比值，其计算式为：

由式(17)可知，均衡电流IVM与fSN成正比关系，因此fSN可作为均衡电流的控制量，可以根据需要调节开关频率达到调节均衡电流大小的目的。

2.3 运行条件

本文中，均衡器设计运行于iLr断续工作模式，此模式下均压器开关损耗小，还具有均衡电流控制简单的优点。工作在断续模式需要模态2 存在反向谐振电流且模态3 不存在谐振电流。

若模态2 存在反向谐振电流，则根据式(15)可知：

若模态3 不存在谐振电流，则：

结合式(14)，由式(20)可得：

根据式(19)和(21)，可得均衡器工作在断续模式的条件为：

由于req很小，可以忽略，式(22)可化简为：

因而，VString与Vp需要满足式(23)的条件限制，均衡器才能工作在断续工作模式。

3 均衡器参数设计

均衡器设计的第一步是选择变压器变比N：当串联超级电容总电压VString和单个超级电容电压VSC范围确定后，由式(2)和(23)可确定变压器变比的取值范围。本文中，VString=24 V，1.5 V

Lr和Cr的选择：首先，当开关频率fS选定后，由于fSN<1/2，可选出谐振频率f0。根据均衡电流IVM和N的取值，由式(17)可得到Z0。最后将得到的f0和Z0代入式(24)求得Lr和Cr。

本文选择fS=120 kHz，fSN=1/4，f0=480 kHz，IVM=0.35 A，Z0=32.74 Ω，进而求得Lr=10.85 μH 和Cr=10.13 nF。

4 实验验证

为了验证分析结果和均衡器的特性，制作了样机并进行了测试。表1 给出了实验样机参数。需要说明的是，为了便于检验均衡效果以及均衡速度，超级电容初始压差设置较大并且均衡电流设置较大。

表1 样机参数

图5 给出了均衡器关键波形的实验结果。图5(a)所示的实验波形与文中工作原理分析吻合(参见图4)，波形中的参数与理论模型计算结果一致。从图5(b)可以看出，由于电流值从零开始谐振上升，开关管两端电压和开关管的电流交叠时间非常短，QH开通损耗非常小，基本上实现了软开关；开关管QH为完全软关断。

图5 关键波形实验结果

采用10 个额定电压2.7 V 的500 F 超级电容串联作为储能部分，各个超级电容的初始电压分别为VSC1=1.5 V，VSC2=VSC3=VSC4=2.3 V，VSC5=VSC6=VSC7=2.5 V，VSC8=VSC9=VSC10=2.7 V，均衡电流设定为0.35 A，开关频率fS=20 kHz，谐振频率f0=480 kHz。均衡过程如图6 所示：电压最低的超级电容优先充电，电压上升，最终各个超级电容电压趋于均衡一致。初始各个超级电容电压的标准差为356 mV，实验结束时各个超级电容的电压的标准差小于10 mV。

图6 均衡测试中超级电容电压变化曲线

5 结论

本文提出的电压均衡器具有可控开关少，控制简单，扩展性强以及易于实现等优点。采用半桥谐振电流断续工作模式保证了所有MOSFET 和二极管都能实现软开关，并且在开环配置的情况下能够控制均衡电流的大小。实验结果验证了数学模型的正确性。所提出的均衡器具有很好的均衡效果：对10 个串联超级电容进行了均衡实验，初始各个超级电容电压的标准差为356 mV，实验结束时各个超级电容的电压的标准差小于10 mV。