基于区间数确定性与不确定性相互作用点的卫生应急能力多属性决策模型

孙爱峰

新型冠状病毒肺炎疫情在全国和世界范围内的大流行,是目前全球面临的头号公共卫生问题[1]。提高医疗和公共卫生机构的卫生应急能力,是保证及时对突发公共卫生事件进行应急处置和对突发事件进行紧急医疗救援的关键因素之一。基于区间灰数多属性群决策建模技术验证疾控机构卫生应急能力评价案例充分利用了区间灰数、属性测度、专家权重及属性群决策信息,具有可行性和推介意义[2]。为提供更多的区间数多属性决策模型,笔者应用基于区间数确定性与不确定性相互作用点的多属性决策方法[3]和基于秩和比法的可信区间法[4]构建新的基于区间数确定性与不确定性相互作用点的多属性决策模型,并再次分析其中的案例资料,为提高卫生应急能力提供参考依据。现报告如下。

一、资料与方法

(一)资料来源

以X1-预案准备、X2-队伍建设、X3-资源保障、X4-监测预警、X5-反应协作作为评价卫生应急能力的指标且均为高优,属性值以介于实数0～1的区间灰数表示,对机构无整体偏好的专家M1、M2论证给出了机构A、B、C的原始属性区间灰数测度矩阵(表1),数据来自文献[2]。

表1 专家M1、M2对机构A、B、C的原始属性测度矩阵

(二)统计方法

1.基于区间数确定性与不确定性相互作用点的多属性决策

该决策模型的基本步骤[3]为:

步骤2:取i=1,计算每个规范化后区间数的相互作用点,即联系数Umnp的模。其计算公式为:

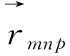
图1 规范化区间数确定性测度和不确定性测度的相互作用

该向量的模在一维空间中的映像即为规范化区间数确定性测度和不确定性测度的相互作用点。见图2。

图2 规范化区间数确定性测度和不确定性测度的相互作用点

步骤4:分别计算基于每一位专家评价数据的各机构加权综合值M(Snp)。其计算公式为:

M(Snp)=Σ|rmnp||rwm|

步骤5:根据文献[2]给定的两位专家分配权重的区间数,按照步骤3计算两位专家权重区间数的相互作用点,按照步骤4计算综合两位专家评价数据的各机构总加权综合值M(Sn)。

步骤6:根据综合决策值排序,排序准则:M(Sn)越大该机构的卫生应急能力越优。

2.基于秩和比的可信区间法

由于计算得到的各机构加权综合值M(Sn)在0～1之间,故可借助基于秩和比的可信区间法[4]对其进行两两比较,以判断不同机构卫生应急能力两两之间的差异是否具有统计学意义。为降低犯第I类错误的概率,应采用Bonferroni法调整检验水准。设定检验水准为0.05,则调整后的检验水准α=0.05/3=0.01667,所对应的标准正态分布界值Zα=2.3940。

二、结果

(一)原始决策矩阵的规范化

由于各指标区间灰数均在0～1之间且为高优指标,如规范化处理可能损失原始数据提供的丰富信息,为便于与文献排序比较,不进行规范化处理。

(二)相互作用点的计算

计算两位专家专家对疾控机构卫生应急能力评价区间数的相互作用点。见表2。

表2 不同机构规范化后区间数相互作用点

(三)计算加权综合值并排序

分别计算两位专家对疾控机构卫生应急能力评价的加权综合值,文献给出专家M1、M2的分配权重为[0.4,0.45]和[0.55,0.6],此时将两位专家对疾控机构卫生应急能力评价的加权综合值作为区间数相互作用点,计算两位专家分配权重的相互作用点分别为0.4031和0.5523,计算综合两位专家对疾控机构卫生应急能力评价的总加权综合值,依据准则可得疾控机构卫生应急能力排序为B>C>A。见表3。

表3 不同疾控机构卫生应急能力的加权综合值计算和排序

(四)不同疾控机构卫生应急能力的两两比较

表4 不同疾控机构卫生应急能力加权综合值比较

三、讨论

集对分析是中国学者赵克勤先生创立的一种研究确定性-不确定性问题的系统方法。区间数是确定性与不确定的对立统一,具有宏观层次和微观层次,确定性处于宏观层次,区间数的两个端点处于宏观层次;区间数端点内的那些点处于微观层次,具有不确定性。区间数相比截面点值适于描述变化范围信息[5],因此,区间数多属性决策可应用集对分析构建数学模型。

本研究选用基于区间数确定性与不确定性相互作用点的多属性决策模型综合评价不同疾控机构的卫生应急能力。即基于区间数[x-,x+]建立同异联系数U=x-+(x+-x-)i,当i在[0,1]之间取值时计算得到的联系数的模r为区间数确定性与不确定性相互作用点,是连接区间数宏观层次与微观层次的节点,构成了区间数确定性层次与不确定性层次之间的中介层,区间数决策问题可在区间数的中介层得到满意解或较满意解,取这些点做相对确定性的数学建模,并以这种点为中心作邻域意义上的不确定分析,使得区间数决策不确定的集对分析既方便又直观,既科学又客观,既有集对分析联系数学建模的独特性,又与其他方法有良好的兼容,使基于集对分析的区间数多属性决策建模和分析方法具有广泛的适用性。

随着经济社会的快速发展,SARS、新冠肺炎等突发公共卫生事件发生频率逐渐增加,卫生应急工作在新时期受到高度重视,并催生了卫生应急医学这一跨学科、多领域的新型边缘学科[6]。卫生应急工作即通过一系列预测、监测、预警、储备等应急准备,实现在突发公共卫生事件发生前后及时展开预防控制工作,构建公共卫生事件应急风险沟通机制[7],形成全员联防联控的卫生应急处置合力[8],实现最大限度保障人民生命安全和社会稳定的目的。卫生应急工作具有潜在性、突发性、不确定性和复杂多样性等特征,决定了提升我国卫生系统应对突发公共卫生事件能力应考虑以法律形式定位公共卫生事业是政府公共服务的主要职责、大力提升公共卫生机构的职能和水平,以满足人民群众日益增长的健康需求[9]。

疾控机构的卫生应急能力在突发公共卫生事件应急处置中具有举足轻重的作用。研究结果显示[10],广西疾控机构应急能力水平较低,市级、县级与城区疾控能力建设存在差距,仍需进一步加强和推进广西疾控应急水平的规范化和标准化,提高疾控应急能力水平。新冠疫情的全球爆发流行,提示我们必须提升疾控机构的卫生应急能力,控制类似疫情的再次出现。研究结果表明[11],新冠疫情后扬州市疾控机构卫生应急能力有较大提高,但仍需进一步加强。疾控机构卫生应急能力与预案准备、队伍建设、资源保障、监测预警、反应协作等息息相关,卫生应急预案应扩大实用性、有效性[12],应重视资源配置的公平性。研究结果显示[13],浙江省区域公共卫生应急能力建设具有较好的公平性,但应进一步加强应急领域的应用研究与技术攻关;应急资源配置的人口公平性优于地理公平性,但存在总量不足、空间分布欠合理等问题,应加大投入保障力度,建立统一的资源储备、调拨、管理体系。

客观评价卫生应急能力可促进突发公共卫生事件预防控制工作的顺利开展,必须选用敏感的评价指标,收集客观真实的数据,应用科学简便的方法进行统计分析。笔者应用基于区间数确定性与不确定性相互作用点的多属性决策模型分析案例资料,结果显示,不同疾控机构卫生应急能力的排序为B>C>A,而原文献应用基于区间灰数多属性群决策建模技术的排序为A>C>B,排序不同的原因可能为所用方法的原理不同所致;同时,原始数据可以看出,两位专家对机构B的两项指标论证区间值都在0.8以上,而原文献将机构B作为最差排序明显不合理,也说明本决策模型是可行的。本研究对疾控机构卫生应急能力排序是基于不确定系数i=1即不确定性转化为确定性时所得结论,应同时对不确定性进行进一步分析[14],即i取[0,1]中其他特征值(如i=0.5或0)时不同疾控机构卫生应急能力排序,此时可指导疾控机构采取不同措施,不断提高整体卫生应急能力。

在上述分析基础上,进一步应用基于秩和比的可信区间法进行两两比较显示,三所疾控机构的卫生应急能力两两之间的差异均无统计学意义(P>0.05),说明其卫生应急能力的差异是由于抽样误差引起的。因此,将基于秩和比的可信区间法耦合到基于区间数确定性与不确定性相互作用点的多属性决策模型,能更加客观地评价不同疾控机构的卫生应急能力;如比较组数较多时,应进一步应用基于秩和比的分档法[15]进行聚类分析。即将基于秩和比的可信区间法或分档法耦合到基于区间数确定性与不确定性相互作用点的多属性决策模型,这样形成的新的基于区间数确定性与不确定性相互作用点多属性决策模型不仅能对不同机构的卫生应急能力进行定性排序评价,还能进行两两比较或聚类分析,得到的结论更为可靠,所得结论更能客观评价不同机构卫生应急能力,有利于卫生健康行政部门以及医疗和公共卫生机构采取有的放矢的策略和措施,不断提高卫生应急能力和水平,为应对突发公共卫生事件和突发事件医疗紧急救援奠定坚实的基础。