基于自适应MPC算法的轨迹跟踪控制研究
2021-07-28张灏琦孙前来李小松孙志毅
王 银,张灏琦,孙前来,李小松,孙志毅
太原科技大学 电子信息工程学院,太原030024
自动驾驶不仅可以减少因操作失误而引起的交通事故的发生率,而且能够提高货物的运输效率,因而自动驾驶技术成为当前国内外自动控制领域研究的热点[1]。
车辆的轨迹跟踪控制环节是自动驾驶系统中重要的一部分。轨迹跟踪是指通过控制车辆转向,使得车辆可以按照给定参考轨迹的路线行驶[2]。
目前,智能车辆的轨迹跟踪控制问题受到了国内外广大专家学者的重视。常用的轨迹跟踪控制算法有鲁棒控制、滑膜控制、模型预测控制(MPC)等。文献[3]提出了一种增益调度、鲁棒、共享的控制器来进行轨迹跟踪。文献[4]中的控制器采用了模糊CMAC 控制方法,该控制器可以消除扰动对系统的影响,使得机器人可以较为精确地跟踪参考轨迹,并且一定程度上提高了行驶稳定性。章仁燮等[5]采用了一种条件积分算法的鲁棒控制方法,控制器由运动学和动力学两部分构成,保证侧向偏差和横摆角速度的渐进稳定,使得试验车辆可以实现跟踪期望轨迹的目标。文献[6]提出的滑膜综合控制器可以降低建模不确定性和扰动时的鲁棒性。而MPC相比于其他控制算法来说,最大的优势是多种约束可以在控制过程中被添加进去[7]。大多数学者都把提高轨迹跟踪精度作为主要控制目标[8-10]。其中,文献[11]把车辆行驶的稳定性也作为了控制目标,通过把前轮转角作为控制量,根据MPC设计相应的控制器,可以实现较为稳定的跟踪参考轨迹。文献[12]提出了一种基于MPC 的新型路径跟踪框架,是一个多层控制系统,包括三个具有固定速度的路径跟踪控制器和一个速度决策控制器,可以根据路径信息主动调整纵向速度,且有良好的跟踪精度。文献[13]采用运动学模型,基于MPC方法设计了考虑车辆动力学、执行器和状态约束的路径跟踪控制器,以前轮转向角为控制变量,使AGV的实际轨迹保持在一定的区域内并满足安全要求。文献[14]设计了集成主动前轮转向和差动制动的MPC 控制器,实现了车辆的横向稳定控制。刘凯等[15]针对越野地形的复杂环境,建立了特殊的车辆动力学模型,并且添加了车辆侧倾安全约束。然后在考虑上述模型及约束条件的基础上,设计了MPC 轨迹跟踪控制器。众多专家学者对MPC 轨迹跟踪控制方面都做了大量的研究,且都有着不错的跟踪精度。但大多数都是处于定速且良好工况,然而实际应用中,车辆经常会处于加速减速且低附着的工况中,使得车速变化幅度大,极易造成轨迹跟踪失败,发生安全事故。
因此针对智能车辆在低附着且变速条件下跟踪控制精确性和稳定性不高的问题,提出一种新型控制框架。通过添加侧偏角约束,以及设计预测时域(Hp)控制器,建立了自适应的MPC 控制器,该控制器能够根据车速的变化,实时产生Hp。在CarSim 与MATLAB/Simulink构建的联合仿真实验平台进行试验,仿真实验结果表明自适应的MPC控制器能够提高智能车辆在低附着且变速条件下跟踪控制的精确性和稳定性。
1 车辆动力学模型
车辆的动力学模型是要作为控制器的预测模型使用,需要在较为准确地描述车辆动力学过程的基础上尽可能地进行简化,以减少控制算法的计算量。因此在车辆动力学建模时,要进行以下理想化假设:(1)忽略车辆垂向运动。(2)忽略车辆的悬架特性。(3)忽略轮胎横、纵向耦合关系。(4)不考虑轮胎的横向载荷转移,以及认为轮距相对于转弯半径可以忽略不计,使用单轨模型来描述车辆。(5)忽略空气阻力。
基于上述假设可以得到车辆的动力学模型,如图1所示。
图1 中,Flf、Flr为前后轮受到的纵向力;Fcf、Fcr为前后轮受到的侧向力;Fxf、Fxr为前后轮受到的x方向的力;Fyf、Fyr为前后轮受到的y方向的力;δf为前轮偏转角;αf为前轮侧偏角;φ为横摆角速度。
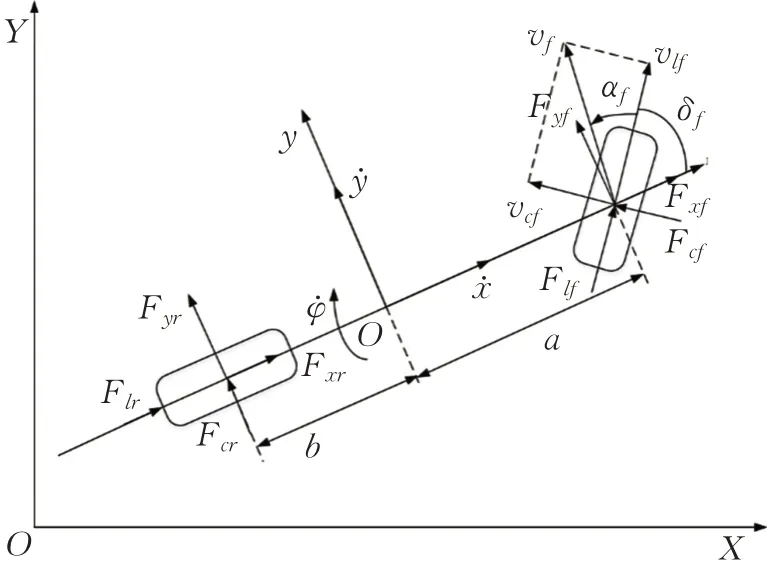
图1 车辆单轨模型
根据牛顿第二定律、车身坐标转换、轮胎受力,可得出车辆动力学模型。
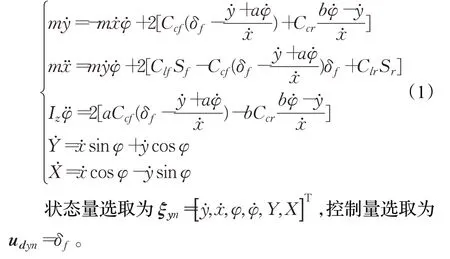
2 轨迹跟踪控制
2.1 轨迹跟踪控制架构
轨迹跟踪控制架构主要由3 部分组成:MPC 控制器、CarSim车辆模型、Hp控制器。其中MPC控制器是实现轨迹跟踪的核心部分,遵循预测模型、滚动优化和反馈校正的基本原理[16]。MPC 控制器根据参考轨迹和目标函数求解出最优的控制量δf,输入到被控车辆模型中,得到当前的状态,作为预测模型的输入,预测时域控制器根据当前车速v求解出对应预测时域Hp,输入到线性误差预测模型中,然后重复上述过程,最终实现轨迹跟踪。图2为基于自适应MPC轨迹跟踪控制器。
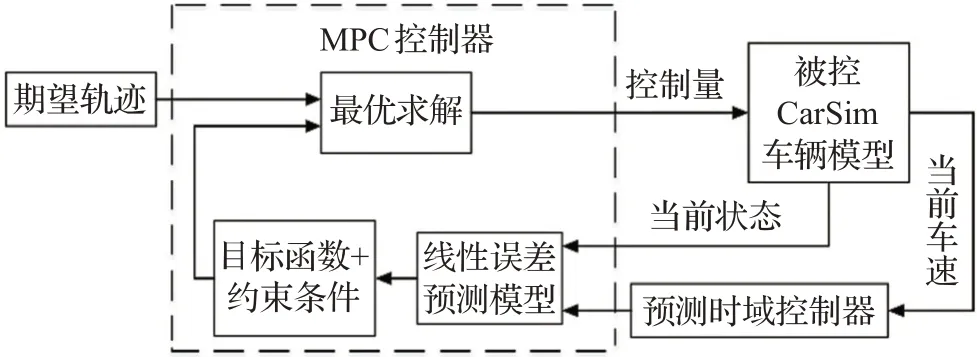
图2 基于自适应MPC轨迹跟踪控制器
2.2 MPC控制器的设计
2.2.1 线性误差模型的建立
根据车辆非线性动力学模型可建立状态空间表达式:

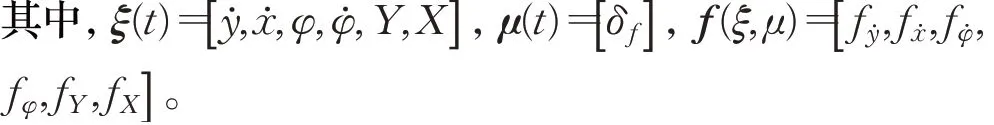
在t时刻将式(2)在工作点(ξ(t),μ(t-1))处线性化并离散化,得到离散的线性时变系统,如下:

根据式(3)、(5)设计模型预测控制器,首先将控制输入由控制量μ(t)经过数学变换转化为控制增量Δμ(t),再做如下设定:

式中,0m×n是m×n维0矩阵;0m是m维列矩阵;Im是m维单位矩阵。
得到线性误差表达式:
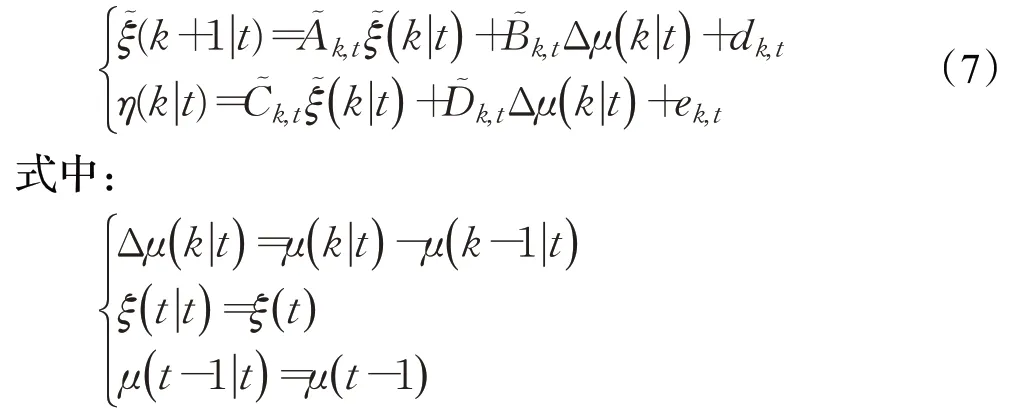
进一步地,可以得到在预测时域内Hp系统输出量可用如下公式计算:
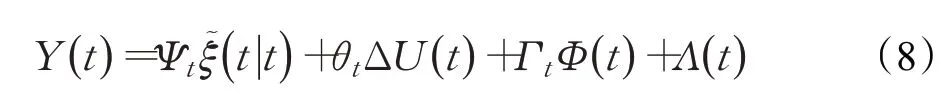
由式(8)可知预测时域Hp内输出量的预测值Ytr(t)可通过当前t时刻已知的状态量ξ(t|t)、上一时刻的控制量μ(t-1|t)以及控制时域Hc内未知的控制增量ΔU(t)计算得到。
2.2.2 目标函数的设计
由于系统的控制增量ΔU(t)是未知的,必须通过设定合理的优化目标进行求解,通过求解目标函数,可以得到一系列最优控制增量,并将序列中的第一个元素加入到状态量和输出量的求解中。
在预测控制中,一般考虑如下目标函数:
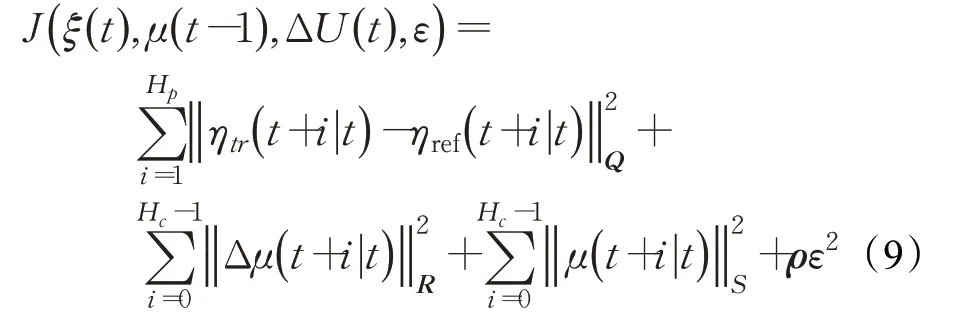
其中,Hp和Hc分别为预测时域和控制时域;ηref(t+i|t)为参考输出量;Q、R、ρ为权重矩阵,ε为松弛因子。
式中第一项体现了控制系统对参考轨迹的跟踪能力,第二项反映了系统对控制量平稳变化的要求,第三项反映了系统对控制量最值的要求。为了防止出现无解的情况,因此在目标函数中加入了松弛因子ε。
2.2.3 约束条件
为了保证系统对期望轨迹的精确跟踪,以及保证行驶的稳定性,需要对控制量、控制增量进行约束,约束条件表达式如下:

此外,为了解决车辆在低附着环境下行驶时因侧滑而造成轨迹跟踪失败,应添加侧偏角约束。
轮胎侧偏角α与质心横向速度、质心纵向速度、横摆角速度以及前轮转角δf之间的关系如下:

将上式进行线性化与离散化处理,得到离散线性时变系统,如下:
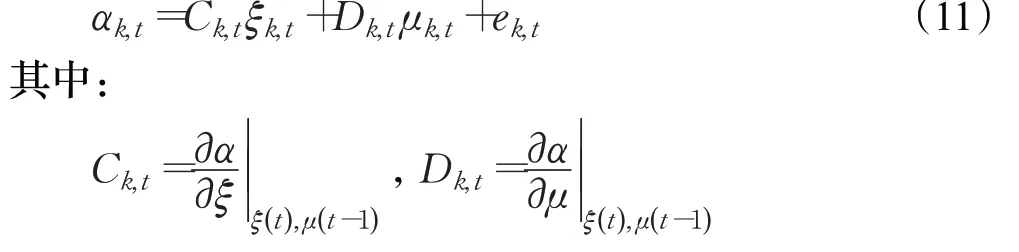

然后对侧偏角添加约束条件:

下面对比未添加侧偏角约束控制器与添加侧偏角约束控制器进行轨迹跟踪的效果。本文参考轨迹如图3所示。表达式如式(13):

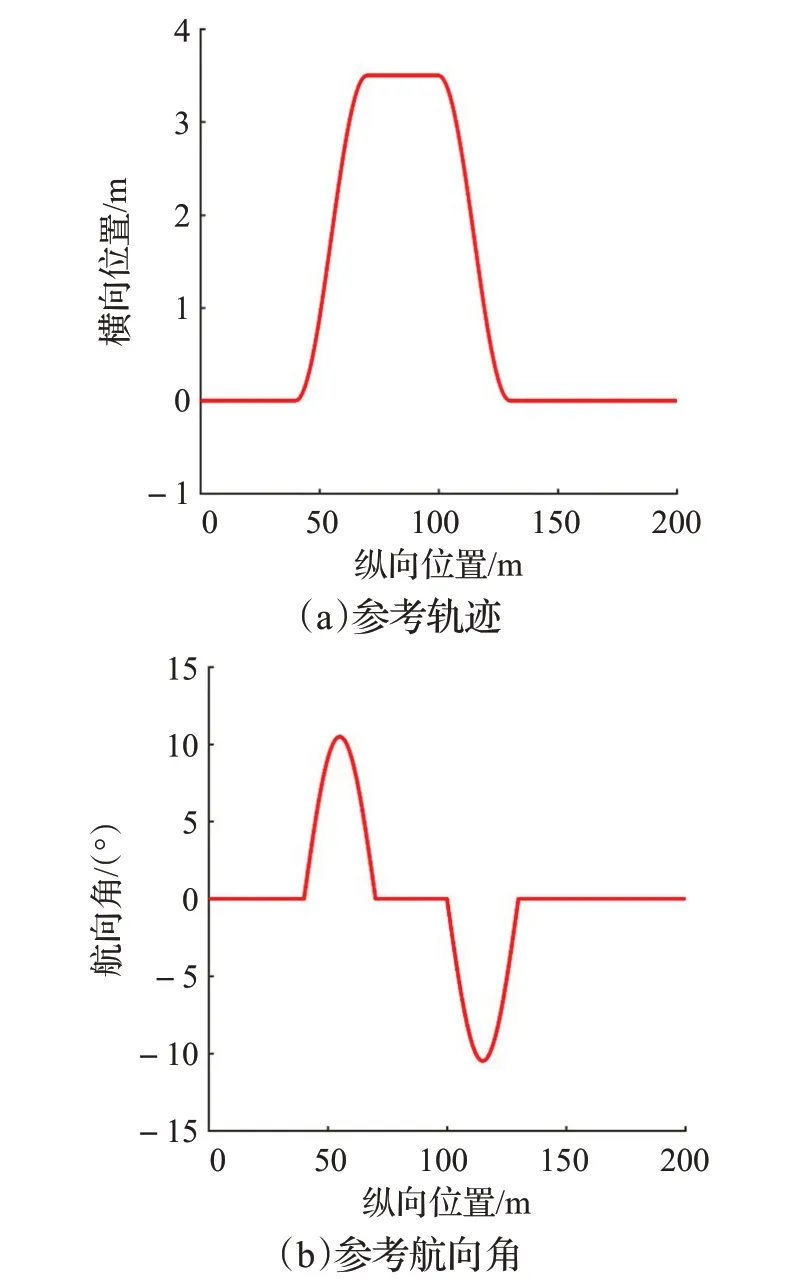
图3 参考轨迹和参考航向
本文车辆参数如表1 所示,MPC 控制器参数如表2所示。

表1 车辆参数
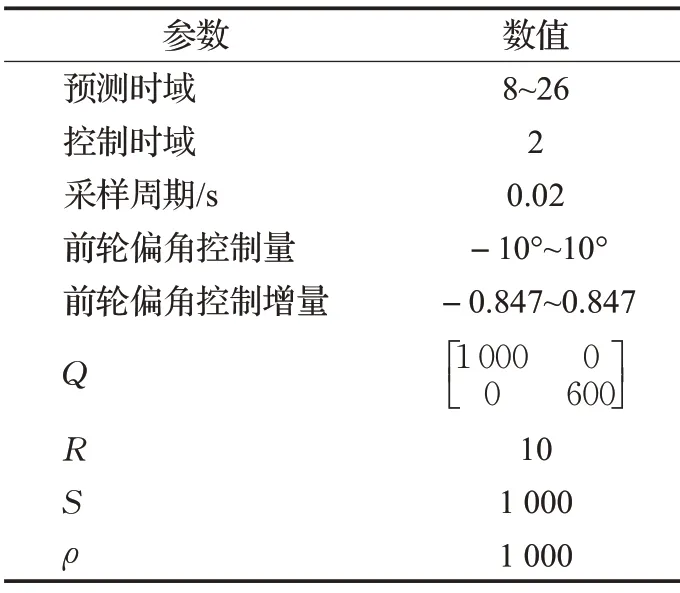
表2 控制器参数
在Carsim 软件中设置路面附着系数为0.2,速度设置为36 km/h,控制器中预测时域设置为8。下面对添加侧偏角约束的MPC控制器和未添加侧偏角约束的MPC控制器分别进行轨迹跟踪控制测试,仿真结果如图4。
在上面的仿真结果中,根据图4(a)和图4(b)可知,控制器添加侧偏角约束能够有效提升车辆轨迹跟踪的精度,其中未添加侧偏角约束的最大横向位置偏差为0.386 3 m,而添加了侧偏角约束的最大横向位置偏差为0.180 2 m。根据图4(c)可知添加侧偏角约束能够有效提升车辆的行驶稳定性,其中未添加侧偏角约束的最大质心侧偏角和横摆角速度分别为3.390 9°和14.081 4(°)/s,而添加了侧偏角约束的最大质心侧偏角和横摆角速度分别为0.729 5°和8.027 9(°)/s。综上所述控制器添加侧偏角约束可以有效提高车辆轨迹跟踪控制的行驶稳定性。
2.3 Hp 控制器的设计
2.3.1 Hp 对轨迹跟踪控制的影响
预测时域作为MPC 的重要参数之一,表示控制器对未来状态的预测程度。若车速一定时,由式(8)以及式(9)中的第一项可知,当Hp较大时,控制器可以预测较远的距离,但会产生较大的误差,降低轨迹跟踪精度;当Hp较小时,在文献[17]提出车辆转向轮的转向角速度约束的影响下,车辆又会因无法及时转向而造成轨迹跟踪失败。所以不同的预测时域产生的控制效果不同。
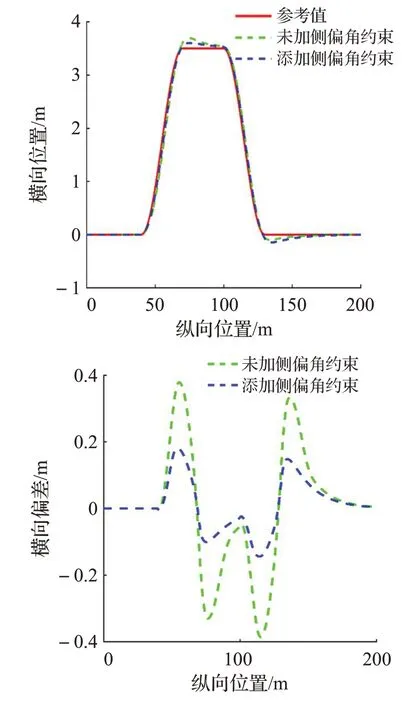
图4(a)横向位置和横向偏差
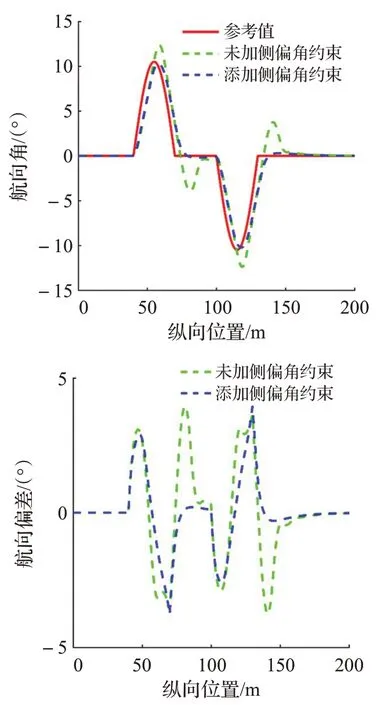
图4(b)航向角和航向偏差
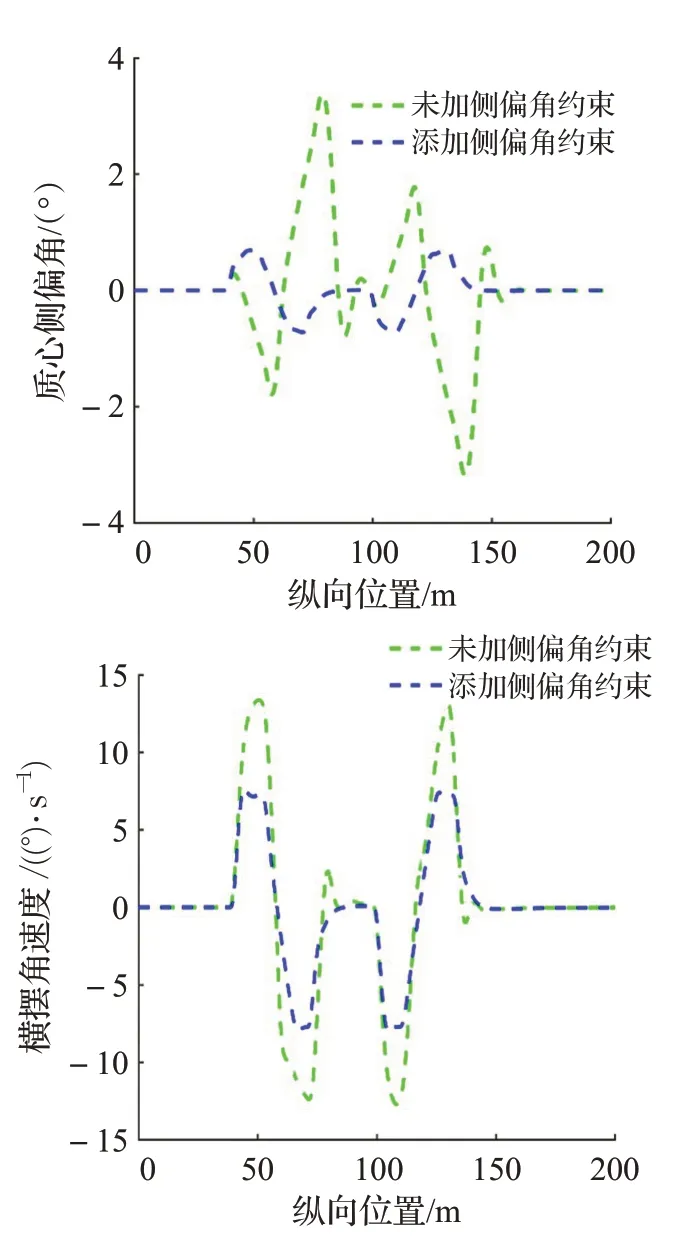
图4(c)质心侧偏角和横摆角速度
下面在添加侧偏角约束的基础上,分析不同恒定速度下Hp取不同的值对轨迹跟踪控制的影响。通过CarSim和MATLAB/Simulink联合仿真进行了四组定速下不同Hp的轨迹跟踪效果的测试,其中Hp也采用了四组。
(1)试验一:36 km/h 下Hp取4 组不同定值的轨迹跟踪。
在试验一的仿真结果中,由图5(c)可知,车速为36 km/h时,Hp取不同定值时轨迹跟踪控制器操作稳定性均较为良好。但随着Hp的增大,轨迹跟踪的精确性随之降低。由图5(a)、图5(b)可知,Hp=8 时,横向偏差和航向偏差最小,Hp=26 时,横向偏差和航向偏差最大。
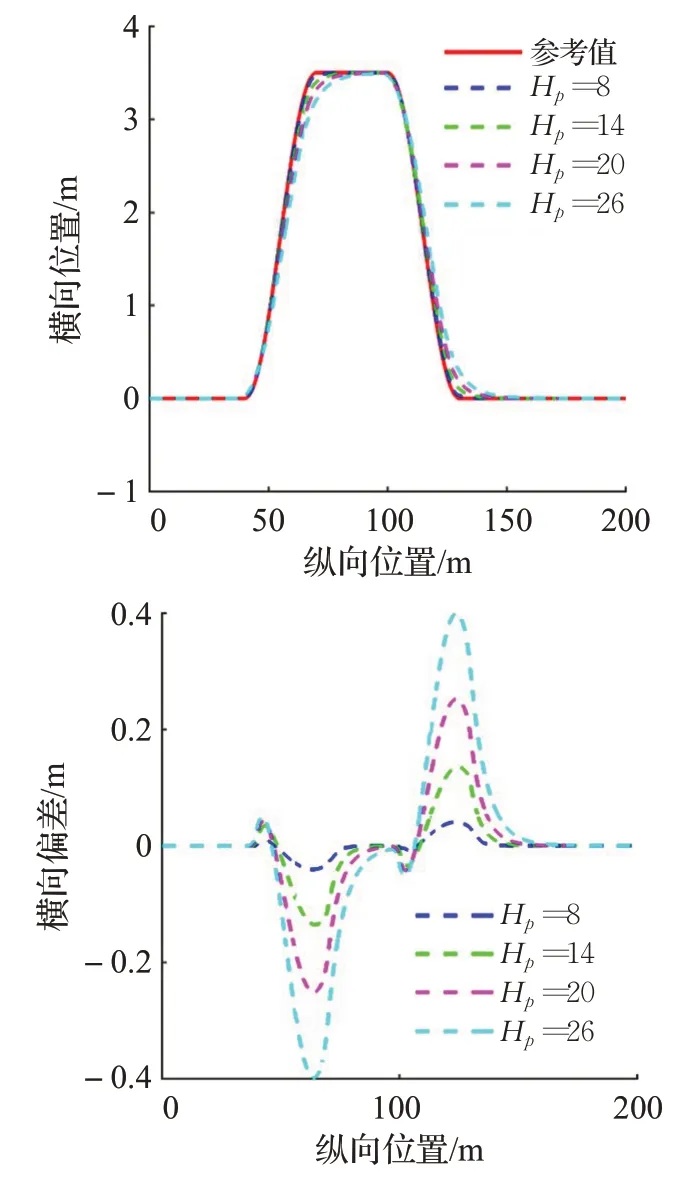
图5(a)36 km/h下的横向位置和横向偏差
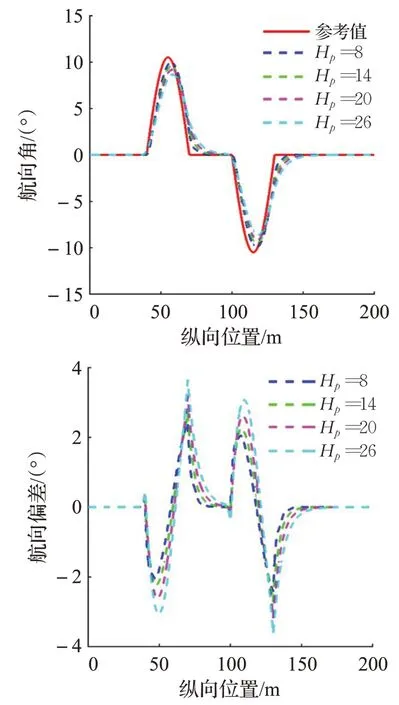
图5(b)36 km/h下的航向角和航向偏差

图5(c)36 km/h下的质心侧偏角和横摆角速度
同理,分别进行72 km/h、90 km/h、108 km/h 下Hp取不同定值的轨迹跟踪。
(2)试验二:72 km/h 下Hp取4 组不同定值的轨迹跟踪,跟踪情况见表3。

表3 试验二跟踪情况
在试验二的仿真结果中,车速为72 km/h时,Hp=8时,虽然横向偏差和航向偏差最小,但质心侧偏角和横摆角速度的数值最大,说明有明显抖动,轨迹跟踪控制器操作稳定性较差。Hp=20 和Hp=26 时,虽然质心侧偏角和横摆角速度较小,但轨迹跟踪的核心参数最大横向偏差较大。而Hp=14 时,虽然横向偏差相较Hp=8来讲要大,但在可接受范围内,且操作稳定性良好。
(3)试验三:90 km/h 下Hp取4 组不同定值的轨迹跟踪,跟踪情况见表4。

表4 试验三跟踪情况
在试验三的仿真结果中,当车速为90 km/h 时,Hp=8 和Hp=14 时,轨迹跟踪失败。Hp=20 和Hp=26时,质心侧偏角和横摆角速度相差不大,都有良好行驶稳定性,但Hp=20 时,轨迹跟踪的核心参数最大横向偏差最小,说明与参考轨迹的误差更小,有更好的跟踪精确性。
(4)试验四:108 km/h下Hp取4组不同定值的轨迹跟踪,跟踪情况见表5。

表5 试验四跟踪情况
在试验四的仿真结果中,车速为108 km/h 时,由仿真结果可知,Hp分别为8、14、20 时轨迹跟踪失败。而Hp=26 时,有良好的跟踪精确性和行驶稳定性。
综上所述,综合考虑跟踪精确性和行驶稳定性,可以得出结论低速时采用较小的Hp,而高速情况下采用较大的Hp有良好的跟踪精确性和行驶稳定性。这是因为在模型预测算法中,当Hp较大时,控制器会考虑更多的未来轨迹趋势变化,造成跟踪精度下降。
2.3.2 Hp 控制器的设计
通过上一节的试验,可知低速工况下,控制器应采用较小的Hp,高速工况下,控制器应采用较大的Hp。然而在轨迹跟踪过程中,行驶工况有时会有变速的要求,那么此时控制器若采用固定的Hp将会无法满足低速、高速、变速的行驶工况。
因此,下面将设计Hp的控制器,能够根据车速度的变化,实时产生Hp。
根据上一节的试验分析,下面根据4组速度对应的Hp,设计变Hp控制器,如表6所示。

表6 不同速度对应的Hp
具体控制规律如式(14)所示,是通过表6选取的四组数据进行三次多项式拟合得到。图6 为不同速度对应的Hp。
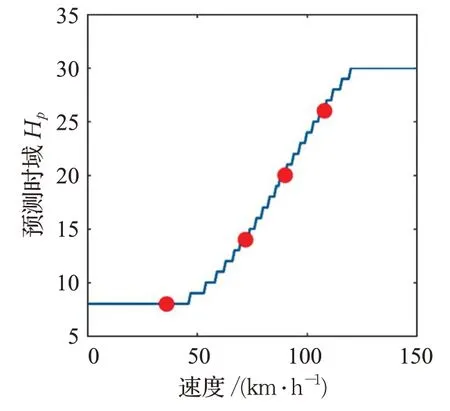
图6 不同速度对应的Hp
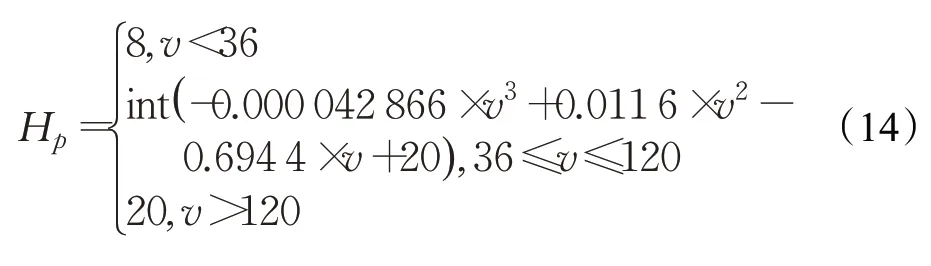
3 仿真分析
前面验证了添加侧偏角约束可以提高车辆在低附着路面轨迹跟踪的精度与行驶稳定性,以及分析了不同速度下Hp取不同值对轨迹跟踪控制的影响。在添加侧偏角约束的基础上结合变Hp控制器,共同构成了自适应MPC轨迹跟踪控制器,下面对自适应MPC轨迹跟踪控制器在变速且低附着环境下进行仿真分析。通过CarSim 和MATLAB/Simulink 搭建联合仿真平台,地面附着系数设置为0.2,为了模拟变速环境,CarSim中设置为超车工况,超车工况速度变化如图7 所示,车辆参数和控制器参数如表1和表2所示。
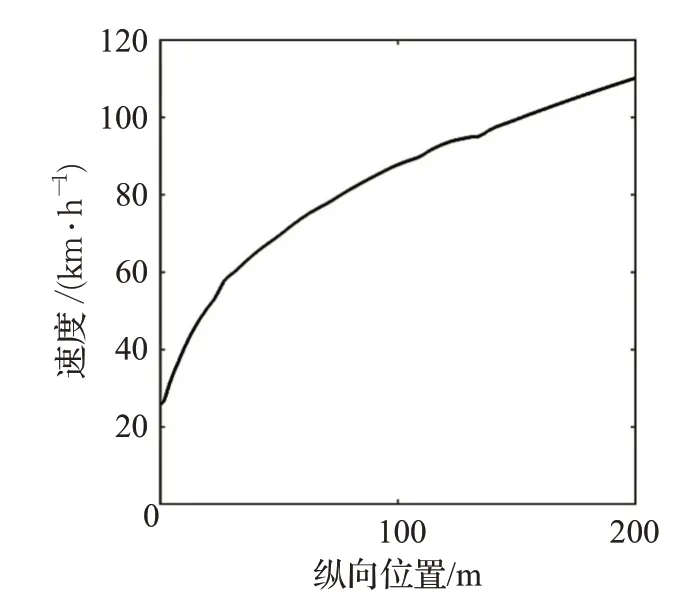
图7 超车工况下速度的变化
在上面的仿真结果中,由图8(a)知Hp分别为8、14、20 时轨迹跟踪失败。Hp=26 时最大横向偏差为0.457 3 m,而自适应的MPC 控制器最大横向偏差为0.385 6 m。由图8(b)可知Hp=26 的最大航向偏差为10.771 1°,而自适应的MPC 控制器的最大航向偏差为2.236 4°。由图8(c)可知Hp=26 最大质心侧偏角和最大横摆角速度分别为11.017 3°和39.867 0(°)/s,而自适应的MPC控制器最大质心侧偏角和最大横摆角速度分别为3.418 9°和26.653 1(°)/s。综上所述,基于自适应的MPC控制器可以有效提高跟踪精度和行驶稳定性。
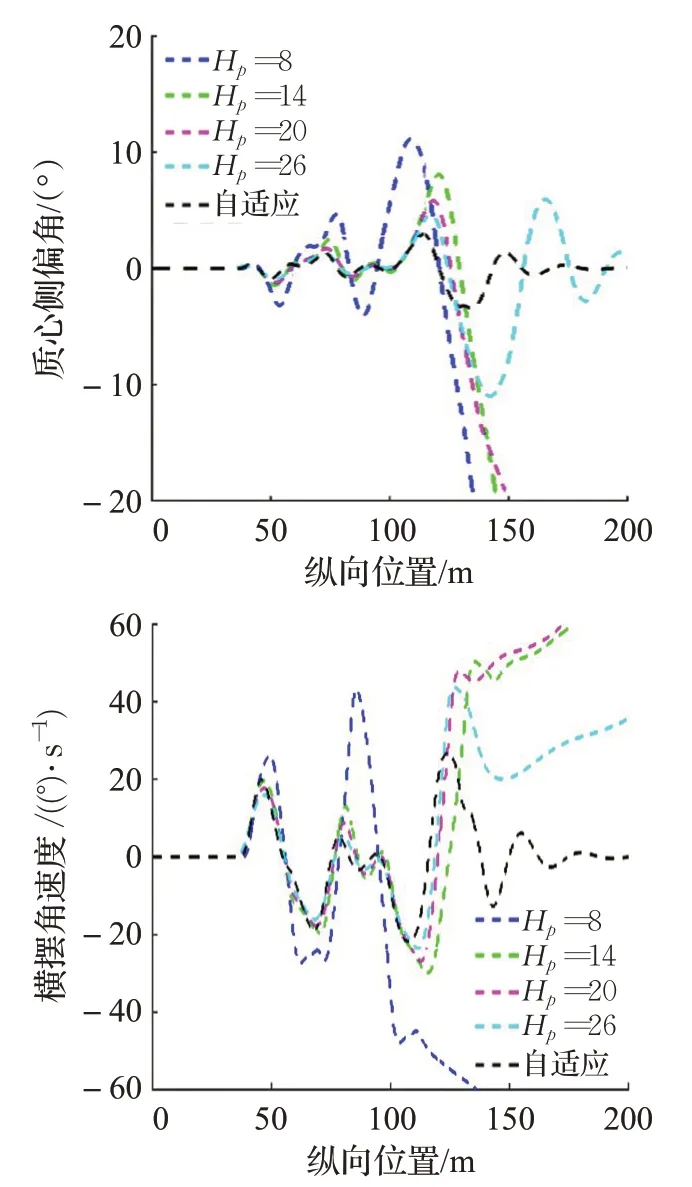
图8(c) 超车工况下的质心侧偏角和横摆角速度
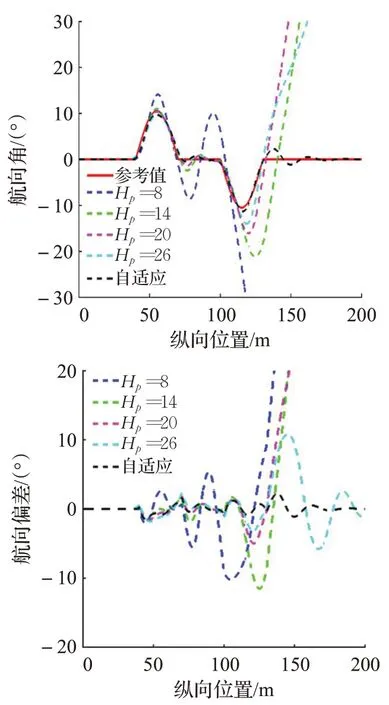
图8(b) 超车工况下的航向角和航向偏差
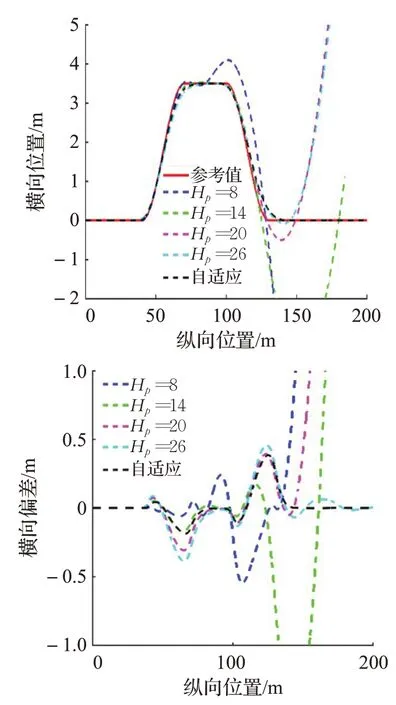
图8(a) 超车工况下的横向位置和横向偏差
4 结论
本文研究了车辆在低附着且变速的环境下轨迹跟踪控制问题。以车辆动力学模型为基础,设计了自适应的MPC控制器,分别由添加侧偏角的MPC控制器和变Hp控制器组成。通过MATLAB/Simulink 和Carsim 联合仿真,所得结论如下:
(1)仿真数据表明,添加侧偏角使得质心侧偏角最大偏差减小了2.661 4°,横摆角速度最大偏差减小了6.053 6(°)/s,有效提高车辆行驶的稳定性。
(2)采用自适应的MPC 控制器,相比无法根据车速更新Hp的控制器,使得最大航向偏差减小了8.534 7°,质心侧偏角减小了7.598 4°,横摆角速度减小了13.215 7(°)/s,有效提高了轨迹跟踪精度和行驶稳定性。
