基于SSA-LSTM的锂离子电池寿命预测 ①

郭 玄，朱 凯

(江苏理工学院汽车与交通工程学院，江苏 常州 213001)

1 前言

电池健康状态(State of Health，简称SOH)表征了电池的容量衰减程度和当前可用容量，对SOH的估计不准确将直接影响电池荷电状态(State of Charge，简称SOC)估算，导致用户对电池状态的错误判断。国内外对SOH有多种定义，主要有：容量、电量、内阻、循环次数和峰值功率等。电池健康状态从电池使用、维护以及经济性表明了在工业应用方面的重要意义，因此研究SOH有利于掌握电池老化因素帮助判断电池的内在隐患和寿命情况。预测SOH的主流方法是数据驱动方法，其不像物理模型方法具备一定物理知识研究，仅需大量数据，通过学习数据内在规律即可描述电池内部的反应[1-3]。然而数据驱动方法存在模型单一或者其模型参数调整难等问题，学者采用优化算法弥补其预测模型的缺陷。目前，针对优化锂电池SOH预测方法的智能算法主要有人工蜂群算法[4]、萤火虫算法[5]、遗传算法[6]、粒子群优化算法[7]等。Karaboga等模拟蜜蜂采蜜原理，以观察蜂、侦查蜂和采蜜蜂之间条件转换，每个蜜源代表一个待求解，因此对算法影响最大的因素为蜜源的开采次数限制，开发力度影响蜜蜂的搜索力度和跳出局部最优的能力[4]。Goldberg等通过模拟自然生物的遗传、进化适应环境变化的特点进行交叉、变异和选择三种操作对参数寻优，但是缺点是求解速度慢，存在局部最小问题[6]。Seyedali等模拟鲸鱼捕食，以包围猎物和气泡网围捕方法具有良好的泛化能力，但缺点是和萤火虫算法相似，前期进行全局搜索，后期进行局部搜索，没有跳出局部最优的操作，从而对复杂问题性能有所下降[8]。He等基于发现者、游荡者、跟随者模型产生的算法，游荡者起到跳出局部最优作用，跟随者作用为局部搜索，发现者引导跟随者，但发现者贡献不多并使得算法实现更复杂[9]。

相比上述多种优化算法，新进算法中的麻雀搜索算法在收敛速度和寻优精度等方面有着明显优势并且结构简单、能准确应对复杂问题[10]。所以针对锂电池长序列数据依赖关系问题，提出SSA-LSTM模型(Sparrow Search Algorithm-Long-Short Term Memory，简称SSA-LSTM)，其中长短期记忆神经网络模型(Long-Short Term Memory，简称LSTM)[11]，对长序列数据不仅具备更好的传递记忆功能，并且能消除反向梯度消失问题，而在预测过程中长短期记忆神经网络模型出现超参数调整困难、收敛速度慢等情况，提出与麻雀搜索算法相结合，形成SSA-LSTM模型，优化LSTM超参数，减小超参数调整困难、收敛速度慢等问题的影响。

2 LSTM长短期记忆神经网络

如图1所示，LSTM是根据循环神经网络(Recurrent Neural Network，简称RNN)改进得来，消除RNN网络的反向传播梯度消失问题，可以保留长短序列依赖关系。LSTM通过遗忘、输入、输出三个结合激励函数，统称为“门”的结构来去除或者增加信息到单元状态。有sigmoid函数将输出0-1之间的数字，代表信息应该通过多少。值为0表示不让任何信息通过，而值为1表示让所有的信息通过，通过这三个门保存和控制单元状态。

图1 LSTM单元Fig.1 LSTM unit.

遗忘层：决定从单元状态中去除哪些信息。其计算公式为：

ft=σ(Wf[ht-1,xt]+bf)

(1)

输出层：同时输出单元状态和隐藏状态给下一层。其计算公式为：

it=σ(Wi[ht-1,xt]+bi)

(2)

(3)

输入层：将旧的单元状态更新为新的单元状态，其计算公式为：

(4)

ot=σ(Wo[ht-1,xt]+bo)

(5)

ht=ot*tanh(Ct)

(6)

其中，ht-1表示为上一单元隐藏层输出，xt表示当前单元输入，Wf和bf分别表示该门的权重和偏置量。

3 麻雀搜索算法

麻雀搜索算法(Sparrow Search Algorithm，简称SSA)是根据麻雀觅食并躲避追捕者的行为提出的一种群智能优化算法，麻雀种群分发现者和跟随者，搜索到较好食物的麻雀为发现者，其余为跟随者，种群中选取一定比例的麻雀带有侦察预警机制的行为动作，发现危险及时放弃食物。麻雀不断搜索更好食物过程即为解的寻优过程。假设麻雀种群数量为N，每代选取种群中位置最好的PN只麻雀作为发现者，N-PN只麻雀作为跟随者，搜索的空间为D维，麻雀的i(i∈1,2,…,n)位置为xi=(xi,1,xi,2,…,xi,D)，麻雀种群最优位置为xb=(xb,1,xb,2,…,xb,D)，在t+1次迭代中，其发现者位置更新为：

(7)

i,j表示第i个麻雀在第j维中的位置信息，itermax表示为最大迭代次数，Q表示为正态分布随机数，L表示为1×d矩阵且其元素均为1。

其追随者位置更新为：

(8)

xworst表示当前全局最差位置，xp表示目前发现者占据的最优位置，表示1×d矩阵，其每个元素随机赋值1或-1，且A+=AT(AAT)-1。

在实验中，假设带有侦察预警机制行为动作的麻雀占总数量的10%-20%，这部分麻雀初始位置在种群中的位置为随机产生，其位置公式为：

(9)

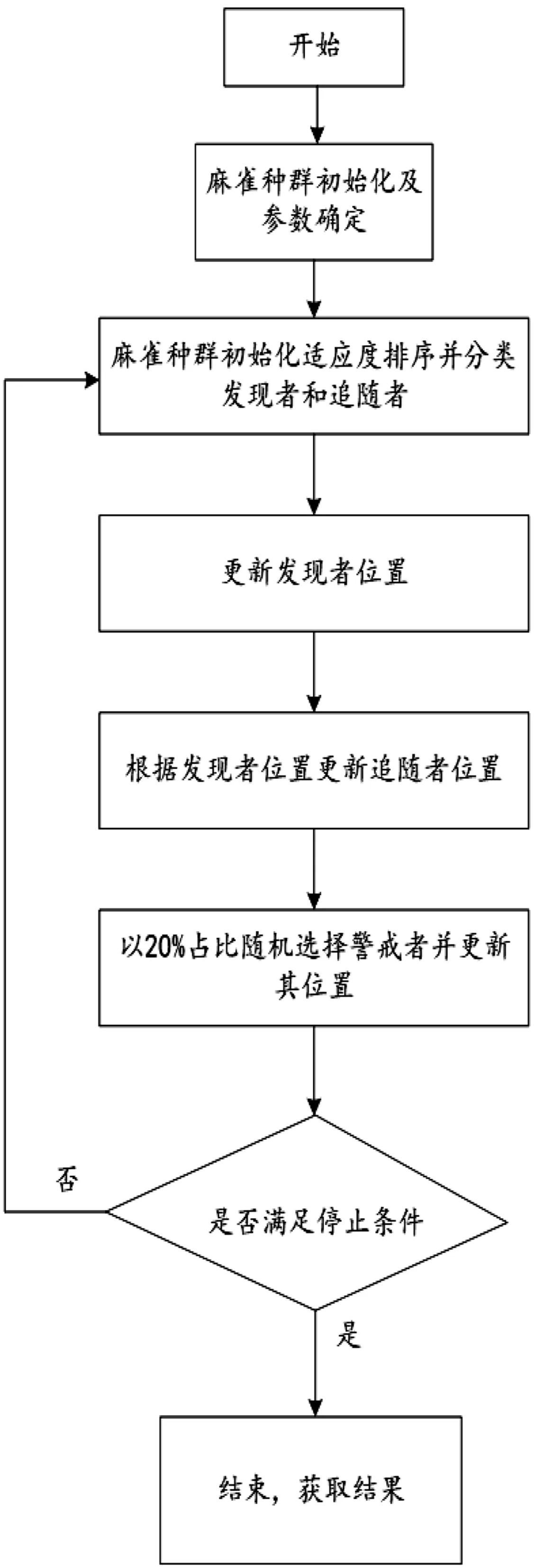
图2 SSA算法流程图Fig.2 SSA algorithm flowchart.

4 SSA-LSTM模型

在LSTM中一般学习率、迭代次数、神经元个数等超参数对预测结果的准确性影响较大，因此将LSTM中的三个参数作为SSA的优化变量，提出SSA-LSTM算法，具体步骤如下：

将每次放电后的电池容量以及对应放电次数数据提取作为预测数据集，为加快最优解求解速度和提高精度，采用简单缩放即min-max标准化方法对数据进行归一化。归一化公式如下：

(10)

其中，x为样本数据，min和max分别表示为样本数据中最小值和最大值，Xnew表示归一化处理后的数据，通过min-max归一化方式对样本数据进行线性变换，结果落于[0,1]区间。

在寻优搜索算法中，确定麻雀种群数量，根据超参数组个数确定麻雀位置loc寻优维度，确定发现者麻雀所占种群比例，一般选取20%。

确定超参数上下边界，初始化麻雀位置loc,loc由寻优超参数组组成。初始化参数包括麻雀最佳位置bestX，全局最佳适应度fMin，最佳适应度pFit等。

将初始化的麻雀位置根据适应度函数评估麻雀位置并进行排序，取前20%为发现者，余者为跟随者，随机选取10%-20%的麻雀携带侦察预警机制动作。

通过发现者、追随者以及预警条件公式更新麻雀位置，接着以边界函数约束超参数并对LSTM所需超参数传参进行预测，返回结果通过适应度函数进行评估位置。若当前麻雀位置适应度优于最佳位置的麻雀适应度则代替，否则不变。若本次迭代中麻雀最佳适应度优于全局最佳适应度则代替，否则不变。

判断是否满足设定的达到误差和最大迭代次数的停止条件。若符合，则将全局最优超参数组设为LSTM的参数；若不符合，则返回4。

具体步骤如图3所示：

图3 SSA-LSTM算法流程图Fig.3 The flowchart of the SSA-LSTM algorithm.

5 实验结果及分析

5.1 数据获取

本实验所用数据来自美国NASA航天局[12]。在锂电池充放电实验中充电截止电压为4.2 V，放电截止电压为2.7 V。数据通过实验方式获取，锂离子电池5号在室温下通过3种不同的操作模式测量：

充电模式：通过1.5 A恒流充电至4.2 V电压水平并且涓流电流为20 mA时停止充电。

放电模式：通过2 A恒流放电至2.7 V电压水平时停止放电。

内阻模式：通过阻抗谱对[0.1,5000]区间频率扫描进行测试。

在实验过程中，通过对电池老化的影响操作并记录电池的放电容量、循环次数、内阻以及温度。随机从数据中选取30%的数据作为测试集，其余作为训练集。输入变量为循环次数、放电电池温度、电池内阻，输出变量为可用容量。

5.2 结果分析

本实验中，麻雀搜索算法参数定义：麻雀种群数量为10，寻优维度为3，麻雀生产者的比例为0.2，搜索算法迭代次数为40，麻雀位置初始化范围(LSTM超参数初始化)分别为：学习率[0.001,0.01]，迭代次数[1,100]，神经元个数[1,100]，LSTM模型由单层LSTM单元组成。对比算法Single-LSTM超参数定义：迭代次数20，学习率0.001，神经元个数100，批次大小16。在获取实验数据并进行预处理后，分别用BP、LSTM、SSA-LSTM算法进行实验对比，图4～6以及子图分别为上述模型的预测对比图，表1为各模型的预测结果比较。

图4 BP预测结果Fig.4 BP prediction result.

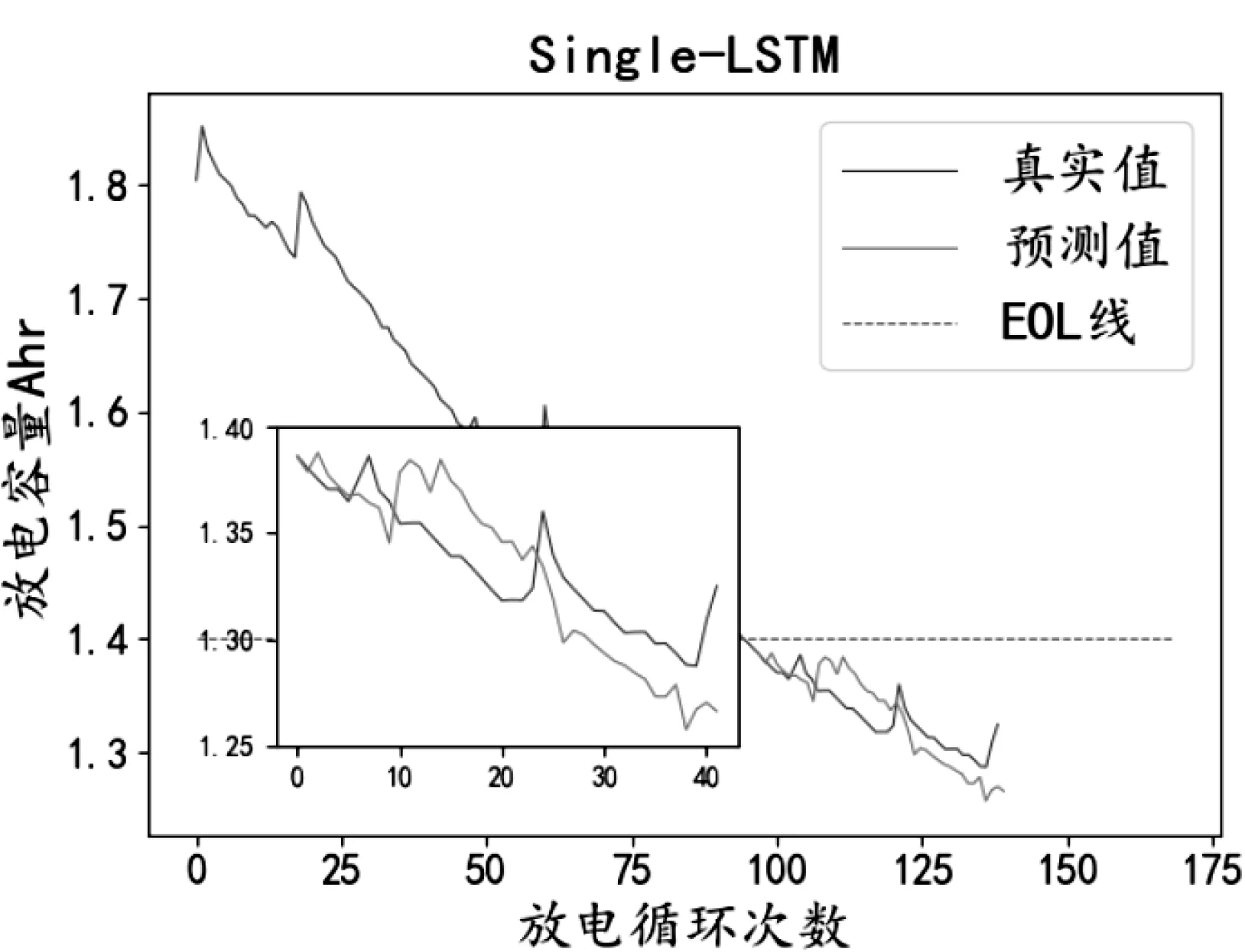
图5 单纯LSTM预测结果Fig.5 Single LSTM prediction result.

图6 SSA-LSTM预测结果Fig.6 SSA-LSTM prediction result.

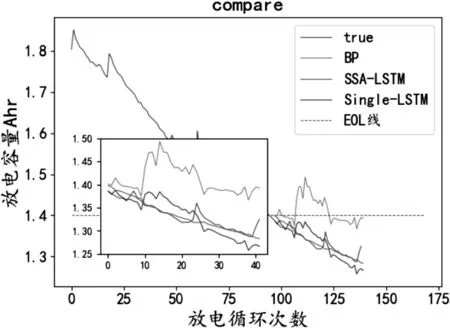
图7 各模型预测结果Fig.7 Prediction results of various models.

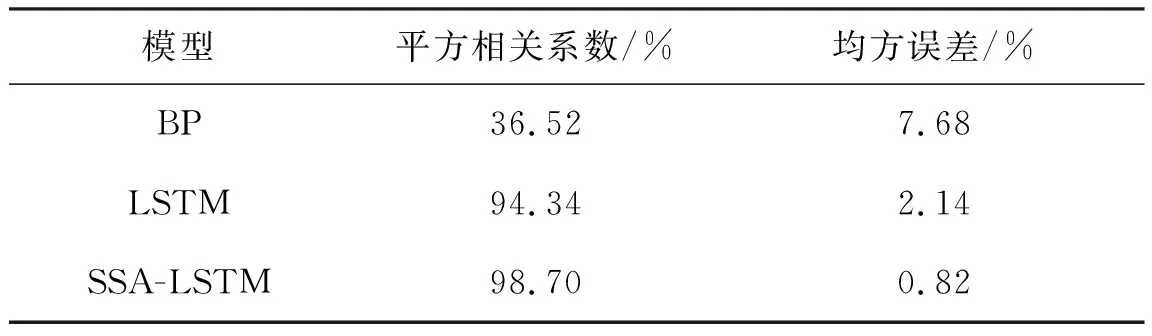
表1 各模型预测结果比较Table 1 Comparison of prediction results of various models.

从图4-5和表1中可以看出相对于BP算法，LSTM算法的均方误差和平方相关系数优化了5.54%、57.82%，证明了LSTM长序列预测性能效果。从图5-6和表1中可以看出SSA-LSTM模型的均方误差和平方相关系数相比LSTM算法在平方相关系数提高了4.36%，在均方误差方面降低了1.32%。并且SSA-LSTM算法通过图6可以看出与真实值拟合良好，说明SSA算法对于优化LSTM超参数具有较好的效果，从而验证了SSA算法的有效性。

6 总结

SSA算法具有较快的收敛速度和强大的搜索能力，采用网格搜索或者枚举搜索等方法对LSTM参数进行寻优时，即耗时较长、精确度也并不高，因此本文利用SSA来优化LSTM的超参数并形成了SSA-LSTM模型。通过Python工具对数据集进行对比试验分析证明：SSA-LSTM模型具有较好的学习能力，是一种有效的LSTM超参数寻优算法。SSA麻雀搜索算法作为目前的新晋算法，因其收敛速度过快和麻雀跳跃式更新方式使其容易陷入局部最优，所以接下来的工作可以从如何跳出局部最优以及麻雀位置更新方式着手。