基于模糊神经网络的脊柱侧弯矫形器设计模型

关天民,赵德竹,梅钊

(1.大连交通大学 机械工程学院，辽宁 大连 116028；2.华柱医疗科技(上海)有限公司 技术部，上海 201204) *

脊柱侧弯是一种常见的三维脊柱畸形疾病，其发病率达2%～3%.在脊柱侧弯的分型中，青少年特发性脊柱侧弯(Adolescent Idiopathic Scoliosis, AIS)是一种发生在青春期、病因不明确的脊柱侧弯，其发病数约占脊柱侧弯患者总数的75%～80%，严重影响青少年正常的脊柱功能.目前，临床上对于脊柱侧弯Cobb角介于25°～40°之间的AIS患者主要采取脊柱侧弯矫形器保守治疗方法[1-2].然而，传统的脊柱侧弯矫形器设计流程繁琐、设计效率低.脊柱侧弯矫形器的设计主要依靠医师的经验，易受其医疗水平及主观因素影响.这导致脊柱侧弯矫形器的设计过程中存在大量的不确定性、非线性信息，难以建立精确的脊柱侧弯矫形器设计数学模型.近年来，随着人工智能技术的不断发展，人工神经网络被广泛地应用到医疗的各个领域.模糊神经网络结合了模糊逻辑与神经网络，同时具备处理不确定性信息和非线性模型学习的能力.当前，在疾病诊断和治疗上的应用[3-6]是模糊神经网络的研究热点，并且都达到了理想的准确性.为了辅助医师进行脊柱侧弯矫形器设计、提高脊柱侧弯矫形器的设计效率，本文提出了一种基于模糊神经网络的脊柱侧弯矫形器设计模型，实现了预测脊柱侧弯矫形器设计参数和自适应调整隶属度函数；并应用于脊柱侧弯矫形器修型调整量的预测；最后通过试验研究验证该设计模型的可行性.

1 脊柱侧弯矫形器设计模型的结构与算法

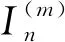
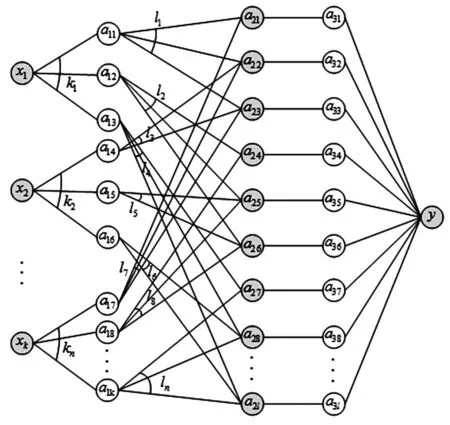
图1 脊柱侧弯矫形器设计模型的结构

(1)

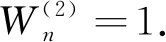
(2)

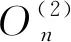
(3)

式中，a、b和c为三角形隶属度函数的参数.

(4)

第四层为输出层，表示输出向量的隶属函数.针对于脊柱侧弯矫形器设计中非线性信息的知识表达，T-S模糊模型通过多条相近线段可以有效地逼近非线性系统.因此，采用T-S型模糊模型表达脊柱侧弯矫形设计规则，其模糊规则的表达形式为：

(5)

式中，

(6)

(7)

(8)

(9)

式中，η为模糊神经网络的自适应学习速率.学习速率决定模型训练过程中神经元连接权值的变化率.为了避免模型训练过程中训练误差出现震荡和收敛速度慢的情况，本文采用的自适应学习速率的计算公式为[8]：

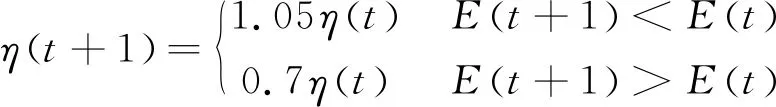
(10)

在模糊逻辑中，隶属度函数往往是领域专家主观确定的，而非最优解.借助BP神经网络的非线性学习能力实现自适应调整隶属度函数.隶属度函数参数δ的调整公式为：

(11)

脊柱侧弯矫形器设计模型结合了模糊逻辑与人工神经网络的优势.借助模糊逻辑实现脊柱侧弯矫形器设计中不确定性信息的表达；借助BP神经网络克服脊柱侧弯矫形器设计中非线性知识建模的难题，实现知识推理和自动知识获取功能.

2 试验研究

试验研究以脊柱侧弯矫形器修型调整量(Δσ)的模糊神经网络预测模型为例，来验证脊柱侧弯矫形器设计模型的可行性.本研究在专家的临床经验和相关研究[9-10]的基础上，选取Cobb角(C)、脊柱侧弯矫形器修型量(σ)、AIS患者综合评判(F)为修型调整量预测模型的输入向量.将{Cobb角，修型量，患者综合评判}映射为该预测模型的输入向量{x1，x2，x3}，修型调整量映射为预测模型的输出值y.定义Cobb角模糊集C= {轻度，中度，重度}；脊柱侧弯矫形器修型量模糊集Q= {少，多}；AIS患者综合评判模糊集F= {舒适，耐受，难受}；脊柱侧弯矫形器修型调整量模糊集R= {少，中，多}.模糊规则库的规则数为18.修型调整量预测模型的结构如图2所示.

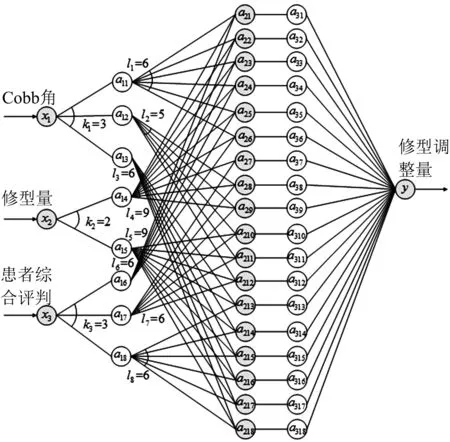
图2 修型调整量预测模型结构

根据专家评判法，由领域专家给出输入向量的隶属度函数.Cobb角模糊集C的隶属度函数为：

(12)

脊柱侧弯矫形器修型量模糊集Q的隶属度函数为：

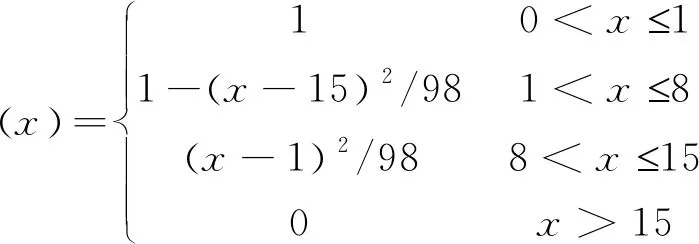
(13)

脊柱侧弯矫形器修型调整量模糊集R的隶属度函数为：

(14)

华柱医疗科技(上海)有限公司提供了60例AIS患者的诊疗实例.其中，男童与女童的人数比例为：37∶23.男童的平均年龄为14.3岁，女童的平均年龄为13.1岁.男童与女童的数据分布均不呈高斯分布.采用经验比例7∶3，确定该预测模型的训练样本数为42，验证样本数为18.在全体样本中按照脊柱侧弯程度分层随机选取42例AIS患者作为训练样本，其中轻度、中度、重度各14例，剩余的18例AIS患者为验证样本.经过分析，训练样本和验证样本的数据分布总体相同.

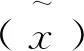
(15)

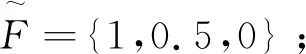
本文利用MATLAB模糊工具箱实现了修型调整量预测模型的建模和学习训练.修型调整量预测模型的测试样本如表1所示.

修型调整量预测模型的测试结果如图3所示.由图3可见，修行调整量预测模型具有良好的逼近性能，最大的偏差出现在测试样本15号，偏差值为0.5 cm.修型调整量预测模型的建模精度为：

(16)

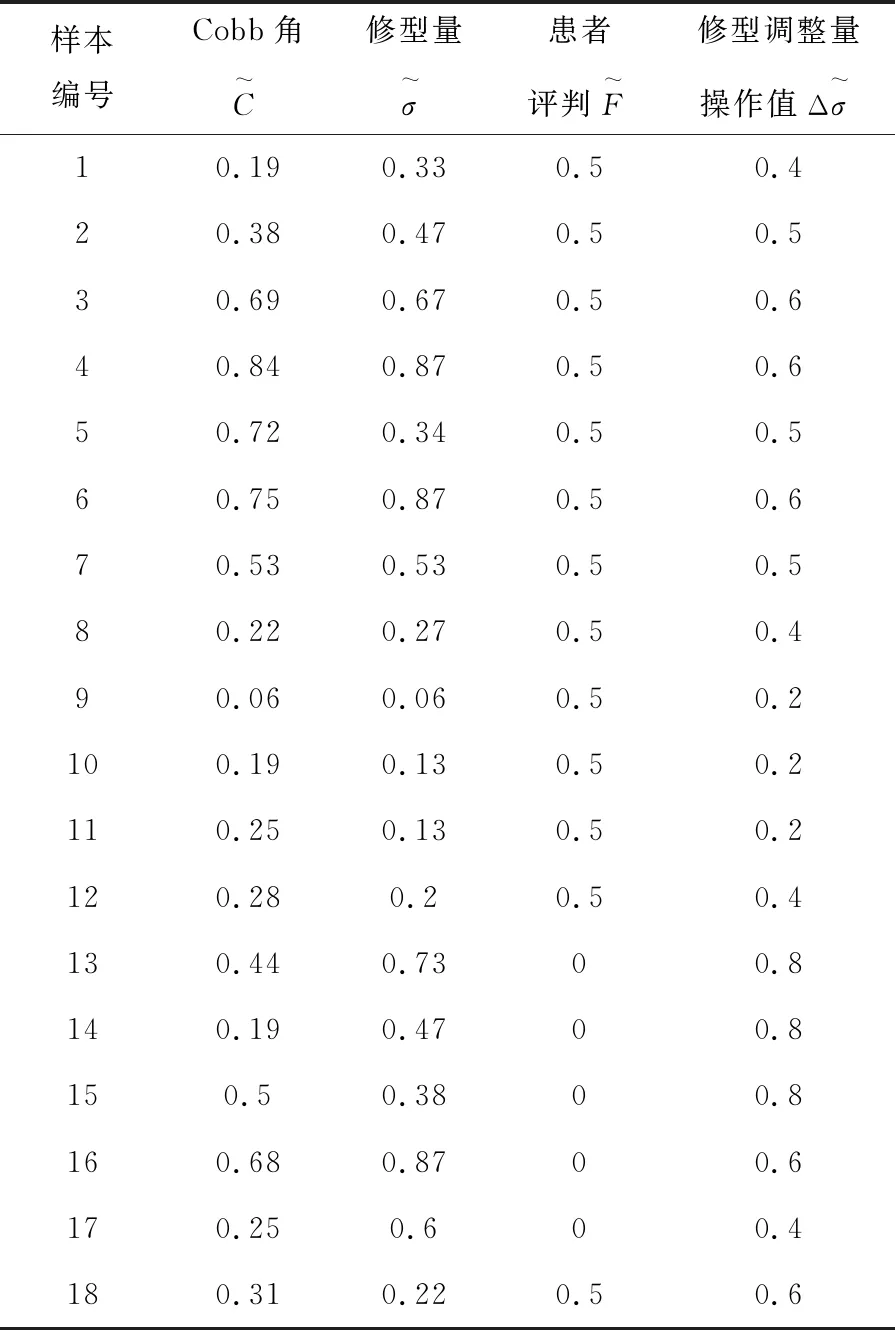
表1 修型调整量预测模型的测试样本

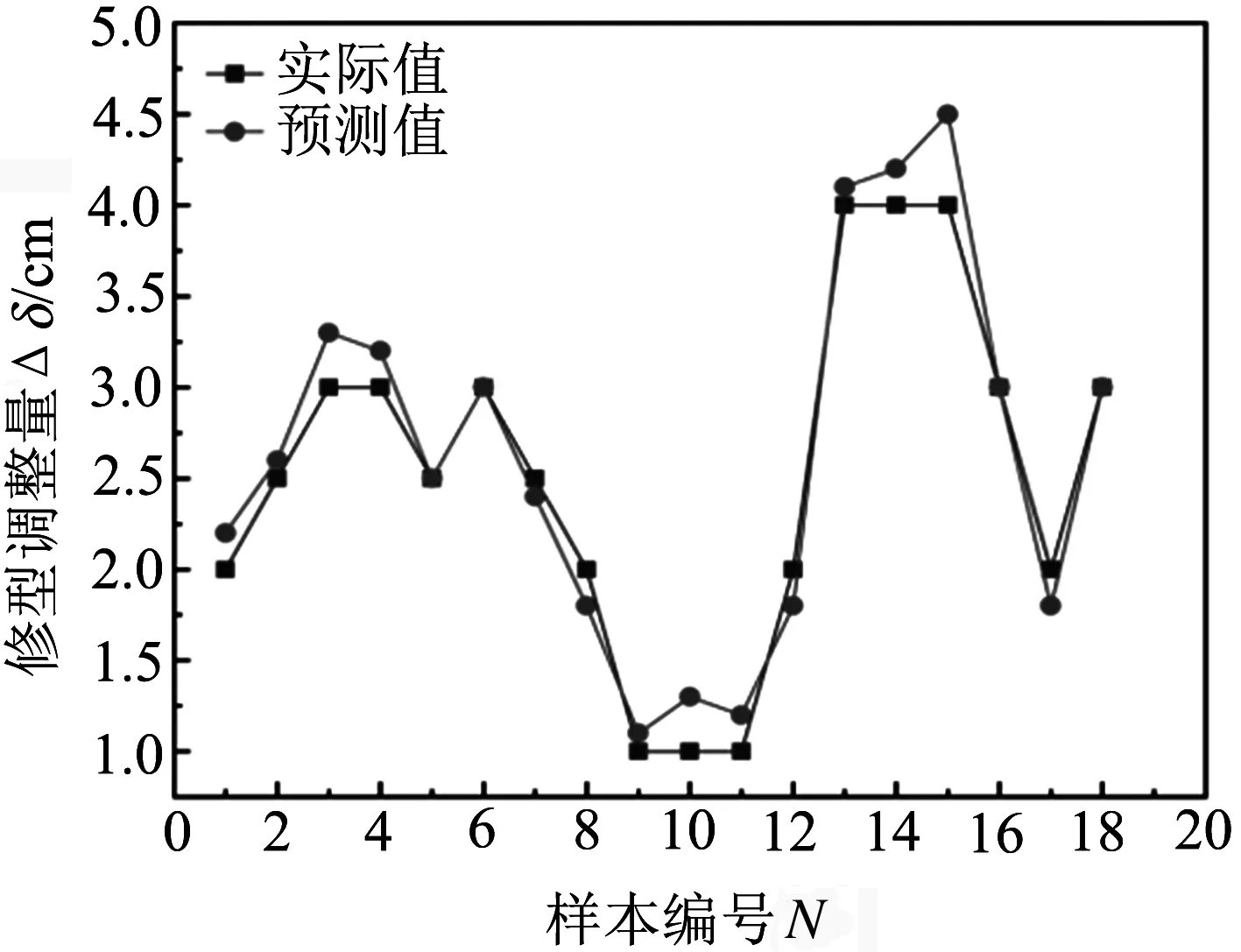
图3 修型调整量预测模型的测试结果

修型调整量预测模型的训练误差如图4所示.由图4可见，随着训练次数的增加，模型的训练误差总体呈下降的趋势.当训练次数达30次后，预测模型的训练误差趋于稳定，达到目标误差10-4.

修型调整量预测模型的回归分析结果如图5所示.由图5可见，样本点集中在最佳回归线附近，表示预测模型的输出和实际值大体上相近；相关系数r为0.841，表示预测值与实际值相关性较好.

图4 修型调整量预测模型的训练误差

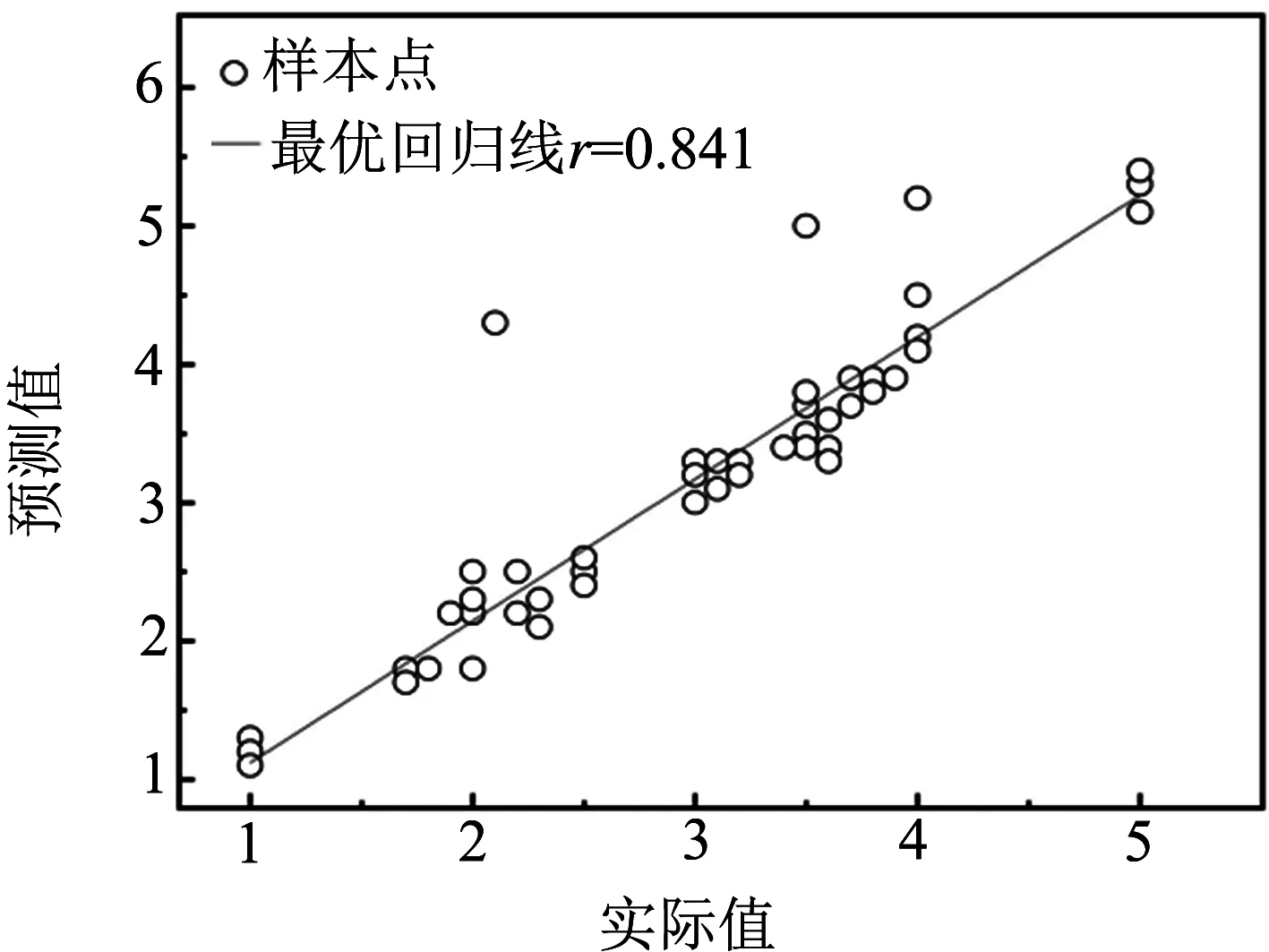
图5 修型调整量预测模型的回归分析结果

修型调整量预测模型学习训练前后设计参数的隶属度函数如图6所示.

(a) Cobb角隶属度函数

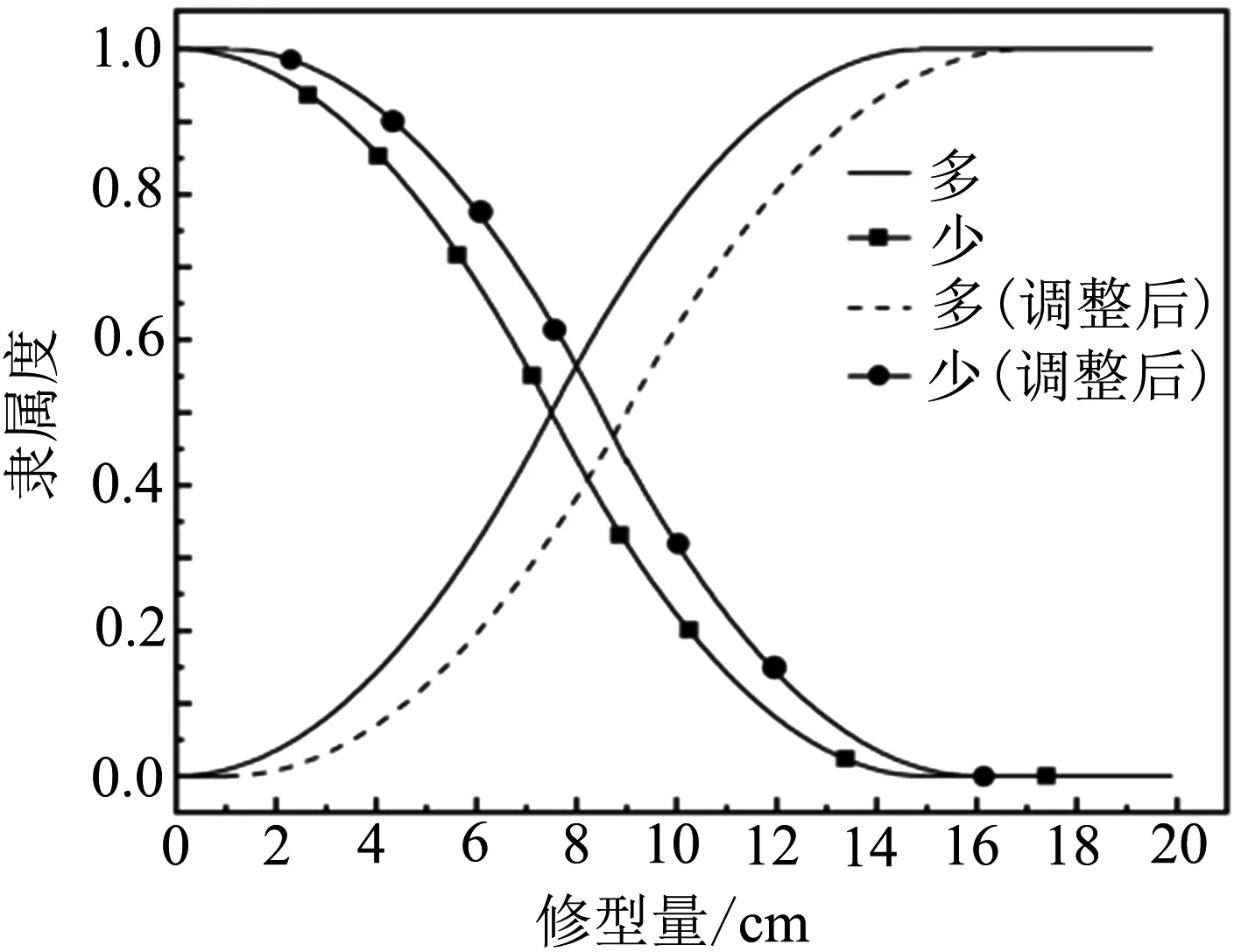
(b) 修型量隶属度函数

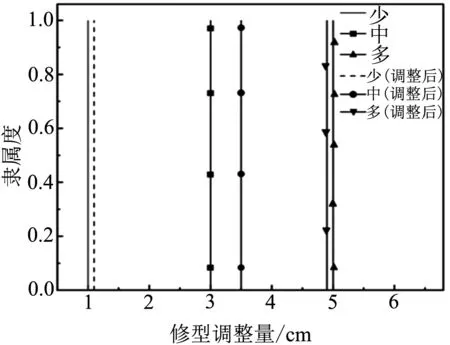
(c)修型调整量隶属度函数图6 修型调整量预测模型学习训练前后设计参数的隶属度函数

修型调整量预测模型于2019年11月在华柱医疗科技(上海)有限公司被成功应用于一例AIS患者的脊柱侧弯矫形器设计实例.患者A：女、13岁、Cobb角30°、Risser Ⅲ级.该预测模型的预测值与专家的操作值如表2所示.该临床试验显示，预测值与领域专家实际操作值的相对误差均未超过0.1.患者A穿戴由修型调整量预测模型辅助设计的3D打印脊柱侧弯矫形器如图7所示.

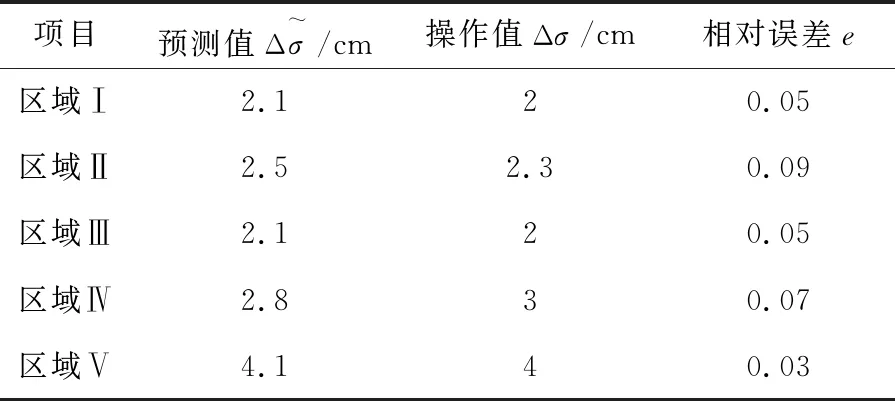
表2 修型调整量预测模型患者A的预测值和实际操作值

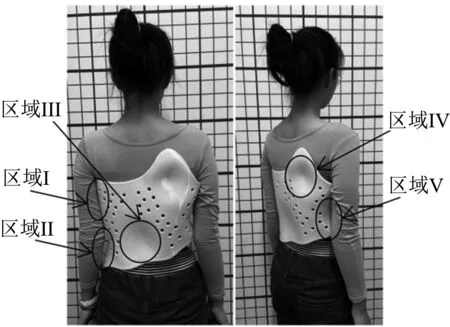
图7 患者A穿戴3D打印的脊柱侧弯矫形器

试验结果显示该预测模型的建模精度为91.9%、预测值和实际值的相关系数为0.841，表明其具备了对脊柱侧弯矫形器修型调整量进行初步预测的能力.从而，验证了基于模糊神经网络的脊柱侧弯矫形器设计模型的可行性.同时，该模型实现了自适应调节隶属度函数的功能.患者A的诊疗实例进一步表明了该设计模型具备临床可行性.

3 结论

为了辅助医师设计脊柱侧弯矫形器，本文提出了一种基于模糊神经网络的脊柱侧弯矫形器设计模型，该模型实现了预测脊柱侧弯矫形器参数并自适应调整隶属度函数.提供了一种有效的脊柱侧弯矫形器辅助设计工具和解决脊柱侧弯矫形器设计中非线性、不确定性信息建模问题的新思路；但是，由于AIS患者的训练样本有限，本文只是初步地建立并验证了脊柱侧弯矫形器设计模型，该设计模型尚未达到最优的建模精度.未来的研究方向可以是通过扩展样本容量等方法，进一步提高该设计模型的准确性.