一类非线性高阶退化拟抛物方程的有限差分方法

李清纯，张继红，梁波

(大连交通大学 理学院，辽宁 大连 116028) *

对于带有p-双调和算子的抛物方程的研究有很多，其中文献[1]提出了当p>2时，如下的退化拟抛物方程：

(1)

本文基于文献[1]所给出的方程考虑下述退化拟抛物方程问题

(2)

其中p≥2为常数，k>0为粘性系数，f(x,t)为关于x,t的二元函数.

在方程(2)中，当p=2时，方程为一个四阶抛物型偏微分方程.近年来关于对四阶抛物方程解的研究受到许多学者的关注：文献[2]对一类四阶抛物型方程构造两层含参数的差分格式，并分析其截断误差证明稳定性；文献[3]基于泛函的极小值原理，利用不动点定理证明一类四阶抛物型方程的定态解的存在性；文献[4]利用有限差分法对带有非线性项的晶体BCF模型进行数值计算，得到了较高的精确结果.

当p>2时，方程为带有p-Laplace算子的退化拟抛物方程.目前关于p-Laplace方程也有不少研究：文献[5]对具有梯度项的p-Laplace方程对应的逼近方程利用最大模估计以及能量估计等证明了其弱解的存在性；文献[6]利用集中紧性原理以及相关不等式研究了含Sobolev临界指数的p-Laplace方程解的存在性问题.

本文将对退化拟抛物方程(2)分p=2和p=3两种情况研究其数值结果.

1 有限差分法

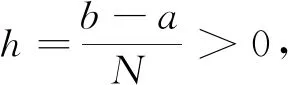
在方程(2)中，不妨假设k=1.

ut-uxxt+(|uxx|p-2uxx)xx=f(x,t)

(3)

接下来对方程(3)中各项方程进行离散.

考虑内网点(xk,tn)处，ut|(xk,tn)-uxxt|(xk,tn)+(|uxx|p-2uxx)xx|(xk,tn)=f(xk,tn)

对导数项ut采用向前差分法：

(4)

对导数项-uxxt采用中心差分法及向前差分法近似：

(5)

(6)

将得到的方程各项代入方程(3)中合并，有

(7)

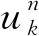
(8)

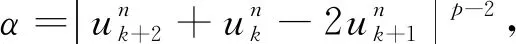
k=2,3,…,N-2，n=0,1,…,M.

本文取xa=a+h,xb=b-h，则初边值条件为

(9)

那么式(8)、(9)就是式(2)当k=1时的有限差分方程.

2 数值实验

下面给出数值实验，a=0,b=π,h=π/30.在差分格式(8)中，分别考虑函数p=2和p=3两种情况，并结合初边值条件方程(9)，就具体算例，给出相应的数值结果.

例1p=2,f(x,t)=2t+sinx，τ=h4，T=0.005，并与方程真实解u(x,t)=t2+sinx进行比较，得到的图像如图1所示，其中实线表示真实解，圆圈表示数值解，图2为相应的绝对误差图.

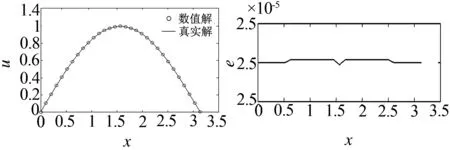
图1 p=2数值解与真实解对比图 图2 p=2绝对误差图

例2f(x,t)=2sinx-2t2·sign(sinx)·sign(t)+3t2·sign(sinx)·sign(t)sin2x+t|sinx|·|t|sinx，p=3,τ=h4，T=0.005，并与方程真实解u(x,t)=tsinx进行比较，可以得到数值解与真实解对比图以及绝对误差结果，如图3、4所示.

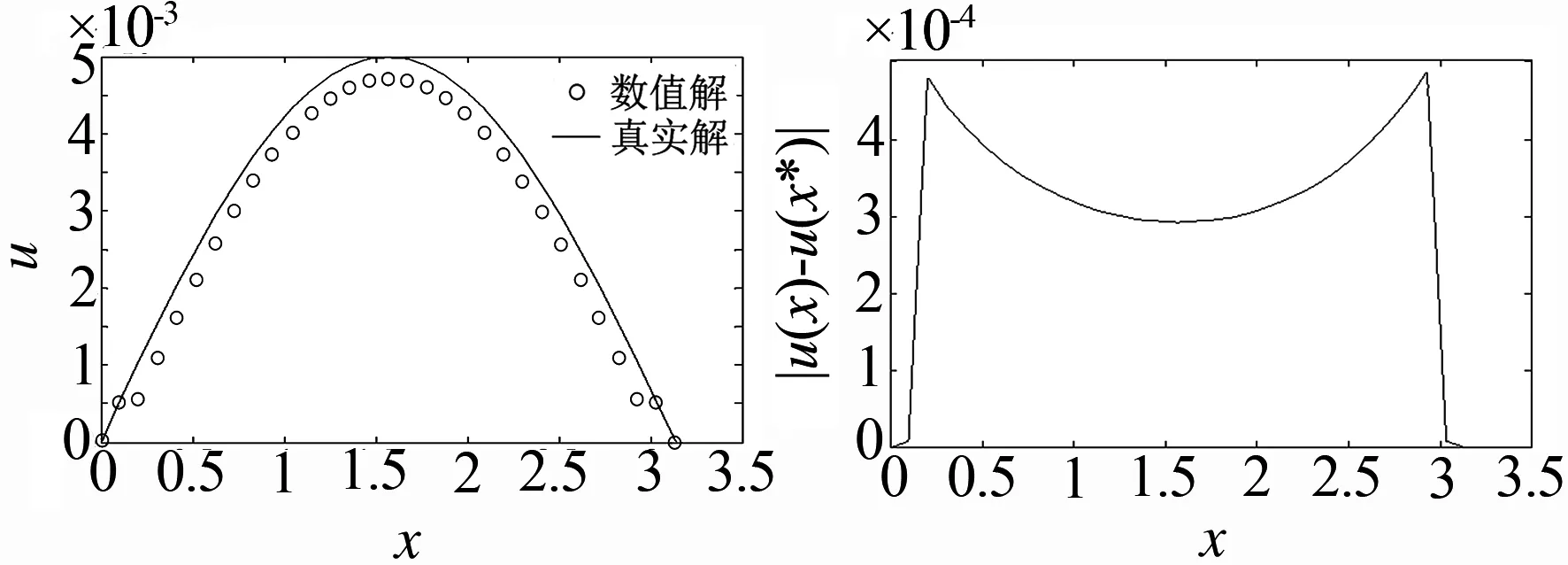
图3 p=3时数值解与真实解对比图 图4 p=3绝对误差图

从图中可以看出，利用有限差分法对含有粘性松弛因子和p-双调和算子的退化拟抛物方程的数值求解是可行的.p=2时的计算结果非常理想，绝对误差可以达到10-5，但是p=3时，由于方程非线性项作用增强，方程变得复杂，所得到的数值结果不太理想.同时两种情况，当时间T较大时，数值计算效果都不太好.

3 结论

本文就有限差分法讨论了一类非线性高阶退化拟抛物方程的数值结果.首先对方程各项的时间和空间导数项，尤其是非线性空间导数项进行了离散化处理，并通过适当的差分逼近，得到了其相应的差分方程.其次选取适当的初边值条件，利用给出的差分格式，通过Matlab软件进行了数值实验.由于本文所研究方程本身是一个极其复杂的，高阶的非线性的偏微分方程，对其进行数值求解，存在着较大的难度.本文也只是做了一个初步的尝试，运用最简便快捷的有限差分法对其进行数值近似，数值结果表明了有限差分法的有效性.但是数值实验也发现，当时间延长时，由于所采用的向前差分格式的局限性，不一定能够保证方法在长时间行为的数值稳定性，同时对时间步长的要求也非常高.这一点需要在今后的研究中进一步进行完善，在保证数值稳定性的前提下，使用尽量简洁快速的算法是下一步的研究目标.