基于扩展概念格的带约束关联分类规则挖掘方法

翟悦,李楠,于文武

(1.大连科技学院 数字技术学院，辽宁 大连116052；2.大连交通大学 软件学院，辽宁 大连 116028) *

近年来采用关联规则构造分类器的关联分类方法广泛应用于医疗、社会服务等领域，然而产生的关联分类规则CARs(Class Association Rules)往往会包含大量冗余规则，对此许多学者展开了带约束的关联分类算法研究，该类算法主要分为事前处理与事后处理两种策略，采用约束事前处理方法如： CBC[1]、FP-growth[2]，这类算法当用户关心的约束条件变化后，算法不得不重新扫描数据库，根据新约束集重新构建分类器，不具备重用性；采用约束事后处理方法如： CCAR[3]、MAC[4]等方法. 该类算法会产生大量候选CARs从而降低算法性能.

本文采用约束事后处理方法，为解决产生候选项目集过多导致效率低下等问题：本文利用扩展概念格结构存储频繁项目集FIs (Frequent Itemsets)，运用结点之间关系定理快速在概念格中搜索符合约束条件的CARs；格结点在信息不丢失的前提条件下大大减少形成分类规则的数量，差集(diffset)概念引入不仅降低格结点内存占用，还能加快对类属性支持度和置信度计算，使得改进后的挖掘算法在时间和空间上具备良好性能.当约束条件变化时无需重新建立概念格，仅需在格上重新搜索.

1 基本定义

1.1 关联分类规则相关概念

设数据库D=(AEC)，其中：一个项目集合由条件属性A={A1,A2,…,An}构成，每一个条件属性Ai可以取某一个特定的值，项目集X={(Ai1,ai1), (Ai2,ai2),…,(Ain,ain)}，类属性C={c1,c2,…,ck}.见表1.

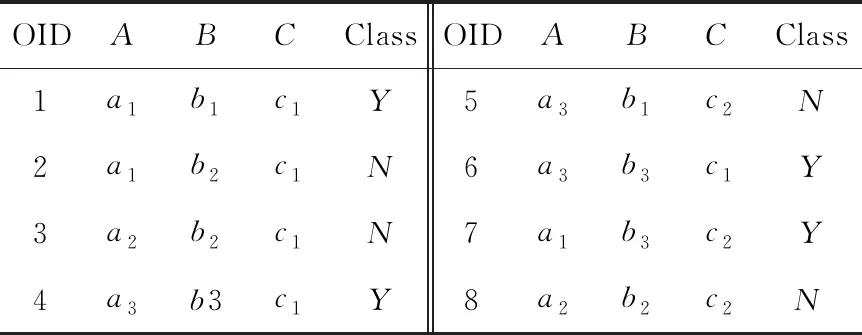
表1 范例数据库D

定义1关联分类规则R形如蕴含式：X→Cj，其中Cj∈C,X为项目集[5]

例如：a3→Y即为一条关联分类规则.

定义2在数据库D中包含项目集X记录集合 记 为 Oidset(X).发 生 数 ActOcc(X) 定 义 为

|Oidset(X)|[6].

例如：Oidset (a3)={4,5,6}.ActOcc (a3)= |Oidset (a3)|=|{4,5,6}|=3.

定义3关联分类规则R的支持数Sup(R)定义为：满足规则的条件属性同时满足类属性记录数目[7].

例如：Sup(a3→Y)=|{4,6}|=2.

定义4关联分类规则R置信度定义为：Conf(R) =Sup(R)/ ActOcc (R)[7].

例如:Conf(a3→Y)= Sup(a3→Y)/ ActOcc (a3) = |{4,6}|/|{4,5,6}|=2/3.

1.2 约束条件

在数据挖掘中常使用的约束类型分为:知识约束、数据约束、层次约束、规则约束、兴趣度约束等.本文研究数据约束，允许用户根据关注目标在规则挖掘过程中加入项目集约束条件，即仅挖掘包含某些项目的规则，使得规则挖掘过程更具效用.

定义5设β为项目集约束条件集,β={X1,X2, …,Xn},其中每个Xi形如ii1∧ii2∧ii3∧……∧ii2∧iik∈I,I={i1,i2,…,im}是m个不同项目的一个集合.

定义6满足约束条件集β的关联分类规则R=X→Cj必须满足：iff∃Xi⊆β，且Xi⊆X[8].

例如: 假设约束集β={<(A,a3),(B,b3)>,},针对第一约束条件<(A,a3),(B,b3)>，形如<(A,a3), (B,b3)>→Y,<(A,a3),(B,b3),(C,c1)>→Y满足约束要求，而规则< (B,b3)>→Y，< (A,a3)>→Y不满足约束要求.针对第二约束条件，形如<(A,a3), (C,c1)>→Y满足约束要求，即规则中包含约束条件中的数据项目.

2 扩展概念格结构

2.1 结点结构与格定义

定义7设T与W为k-项集，它们共同拥有相同 (k-1)-项集作为前缀，由T直接生成其孩子结点(k+1)-项集记为：childrenEC(T)={TX|TX∈(k+1)-项集，且X属于W后项}[9].

定义8设T为k-项集，由T间接生成孩子结点(k+1)-项集记为:childrenL(T)={Y|Y∈(k+1)-项集，T⊂Y,Y⊄childrenEC(T)}[9].

例如：图1所示，其中由T直接生成的孩子结点childrenEC(T)均表示为实线，由T间接生成的孩子结点childrenL(T)均表示为虚线.假设T为bc，根据定义7由T直接生成的(k+1)-项集childrenEC(bc) ={bcd},根据定义8由T间接

图1 概念格结点链接过程

生成的孩子结点childrenL(bc)={abc}.定义9扩展概念格第一层结点定义为五元组Node表示，其中：

(1)id为存储结点id，根据该项目集所包含属性二进制表示.

(2)atts属性集为频繁1-项集.

(3)Oidset(o1,o2,…om)记录集为包含(2)中属性集atts在每个类属性中的集合.

(4)countL(c1,c2,…ck)为统计(3)中记录集在每一个类属性中的数目ci=|oi|.

(5)pos为maxi∈[1,j]{Ci},如果每个分类的统计值相等，则pos默认为C1.

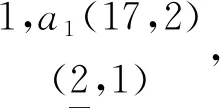
2.2 差集概念diffset

差集概念首先由Zaki等人[10]在2003年提出，本文将差集引入关联分类规则挖掘，在扩展概念格高层的结点所存储信息中，使用差集替代定义9中Oidset，可有效减少格中结点所占用存储空间，还能利用差集快速计算类属性的支持数和置信度.

定义10假设两个项目集PX与PY均以P为前缀的等价类，d(PXY)= Oidset (PX)- Oidset (PY)[11].

定理1已知两个项目集PX、PY与d(PX)、d(PY)，可证明d(PXY)=d(PX) -d(PY).

证明：因为d(PXY)= Oidset (PX)-Oidset (PY)=Oidset(PX)-Oidset(PY)+Oidset(P)-Oidset(P)=(Oidset (P)-Oidset(PY))- (Oidset(P)- Oidset(PX))=d(PY)-d(PX).差集计算示意如图2所示.

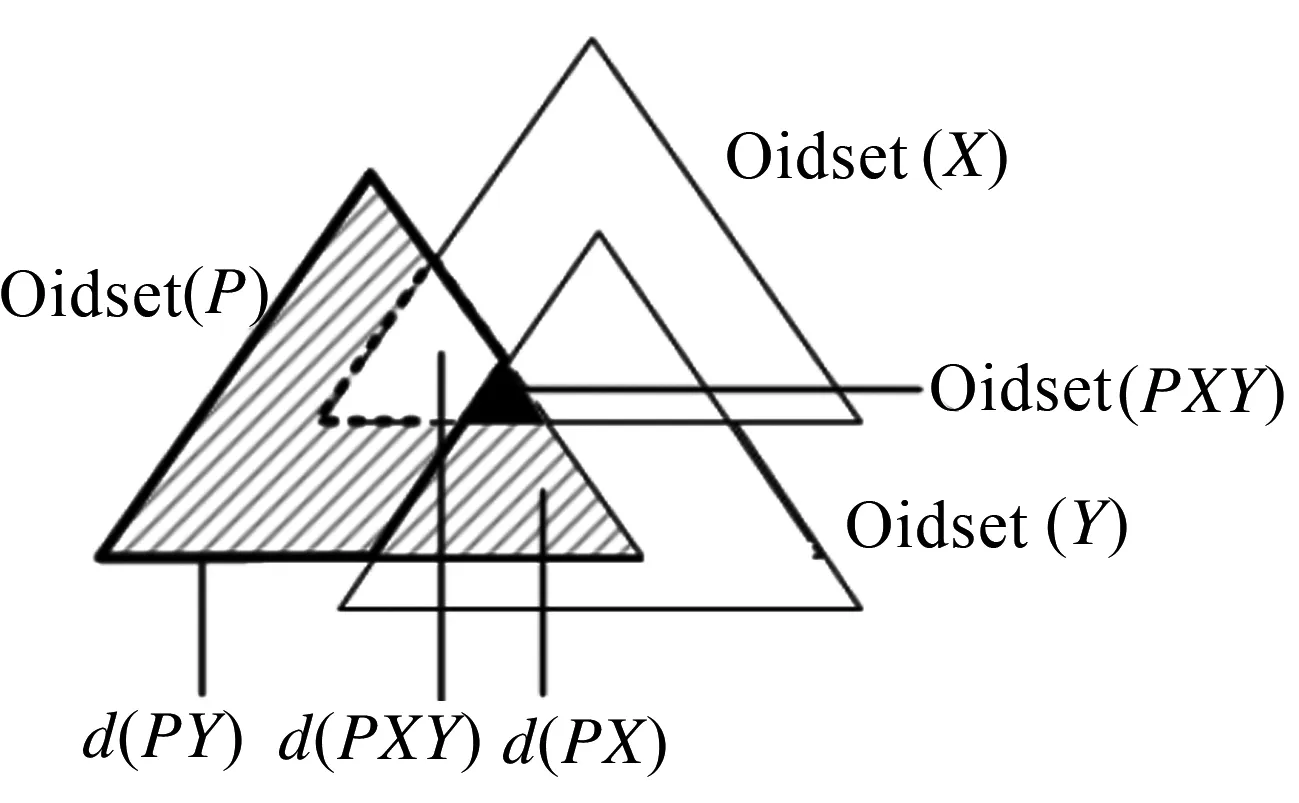
图2 差集计算过程

定义11扩展概念格高层次的结点定义为五元组Node(id, atts, diffset(d1,d2,…dk), countL(c1,c2,…ck) ,pos)表示，其中：

(1) diffset(d1,d2,…，dk)为对应记录集oi的差集.

(2)countL(c1,c2,…，ck)为计算方法公式ci=X.ci- |diffseti|.

(3) 其他结点信息与定义9一致.

图3 扩展概念格结点链接举例

3 扩展概念格构建方法

3.1 相关定理

定理2已知两个概念格中结点X、Y，如果两个结点具有相同的条件属性，且属性值不相等，则Oidset(X)∩Oidset(Y)=∅.

定理3已知概念格中两个结点XA、XB，如果∀XB∈childrenEC(X),且XA结点先与XB生成,则∃Y∈childrenEC(XB)∪children(XB),使得Y∈children(XA).

定理3说明扩展概念格中childrenL(XA)间接孩子结点确定时仅需搜索满足如下条件的结点，条件1：Y∈children(X);条件2：YZ∈childrenEC(Y);条件3：判断如果XA⊂YZ，那么YZ∈children(XA).运用定理3削减了大量候选项目集结点.

3.2 基于差集的扩展概念格构建算法

本文提供一种基于差集的扩展概念格结构LD (Lattice basedDiffset)，该结构包含全部的频繁项目集信息.基于差集的扩展概念格LD生成算法Build_LD步骤如下:

步骤1：输入数据库D，初始化最小支持度minsup；初始化扩展概念格Li←∅;

步骤2：搜索数据库D生成满足minsup的频繁1-项集，调用概念格更新算法构建Lr，生成扩展概念格第1层结点;

步骤3：进行格结点链接操作，根据定理2，如果lx.id≠ly.id，使用lx.Oidset∪ly.Oidset计算格中结点的记录集;

步骤4：根据定义9和定理1，如果lx为概念格第2层结点，使用Oidset(lx) -Oidset(ly)计算格结点差集，如果lx为高层次结点，使用ly.diffseti-lx.diffseti计算格结点差集;

步骤5：统计步骤3中记录集在每一个类属性中的数目ci=|oi|.计算pos并标记;

步骤 6：如果pos≥minsup,则调用概念格更新算法，更新lx.childrenEC和ly.childrenL,转步骤3;

3.3 基于差集的扩展概念格构建实例

首先针对表1所示数据库D(minsup=25%)，利用Build_LD算法产生的扩展概念格结构见图4.扩展概念格LD根结点为空结点，调用Build_LD算法生成扩展概念格第一层结点为〈{a1},{a2},{a3},{b1}, {b2}, {b3},{c1},{c2}〉,其中{b1}结点2,b1(1,5)(1,1)不满足最小支持度minsup要求，故LD中不产生该结点.此后根据定义11和定理2生成第二层结点，分别为〈{a1b2},{a1b3},{a1c1},{a1c2},{a2b2},{a2b3},{a2c1},{a2c2},{a3b2},{a3b3},{a3c1},{a3c2},{b2c1},{b2c2},{b3c1},{b3c2}〉.其中仅有〈{a2b2}, {a3b3},{a3c1},{b2c1},{b3c1}〉五个结点满足最小支持度minsup要求.如图5(a)所示，计算结点3,a3b2(46,5)(0,0)不满足minsup要求，不产生该结点.由算法Build_LD可知，生成概念格二层结点差集计算公式为O.diffseti= Oidset(lx) -Oidset(ly)，而在计算高层概念格结点差集计算公式为O.diffseti=ly.diffseti-lx.diffseti.如图5(b)所示.

图4 表1构建扩展概念格结构

图5 扩展概念格二层结点与高层结点计算过程

图4展示出算法1的执行过程，可以看出根据算法Build_LD构建基于差集的扩展概念格有效缩减了结点数目，FIs又在不丢失有效信息的前提下降低了建造整个格的复杂度.差集的运用进一步节省了存储空间和计算时间.

4 带约束关联分类规则提取

在约束型关联分类规则挖掘过程中，约束条件会随着实际应用场景中用户需求而不断变化，本文提出规则提取算法是在构建的扩展概念格结构上进行挖掘，LD结构本身包含频繁项目集完整信息，以便于当约束条件改变，仅需按照新约束条件在LD中重新搜索且无需重复构建格，从而加快挖掘速度.

4.1 带约束的关联分类规则提取算法LD-CAR

在带项目集约束下，本文提供一种基于差集的概念格提取关联分类规则方法LD-CAR (Diffset and Lattice based algorithm for CAR mining)，该算法挖掘步骤如下：首先根据算法Build_LD建立完成的基于差集的概念格结构，遍历概念格LD，根据用户给定约束集生成符合条件的CARs，并为符合约束结点做flag标记；然后算法清空结点flag标记以备下次利用新约束进行扫描.带约束的关联分类规则提取算法Find_CARs步骤如下：

步骤1:输入LD，初始化约束条件集β,最小置信度minconf;

步骤2:遍历LD中结点，对于每个itemseti∈β，搜索LD寻找包含itemseti的结点li;

步骤3:判断如果ifl.flag=false且conf≥minconf，则将该规则并入CARs中，CARs←CARs∪{l.itemset→cpos},设置l.flag=true;

步骤4:递归调用遍历LD中结点方法;

步骤5:输出满足约束条件集β的关联分类规则；

步骤6:重置LD结点的flag=false,以 便给定下一组新的约束条件下继续生成CARs.

4.2 带约束的关联分类规则提取实例

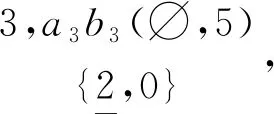
Ruler1: ;

Ruler2: ;

Ruler3: ;

Ruler4: ;

Ruler5: ;

Ruler6: ;

Find_CARs算法挖掘出的关联分类规则集是满足约束添加下的不重复完备规则集.在Find_CARs算法最后一步将全部结点flag标签重置以备下一组新约束集的挖掘.

5 实验结果

为了进一步验证算法的有效性，实验主要比较本文算法LD-CAR、文献3所提到的CCAR算法和文献4提出的MAC算法3者之间的性能差异.测试的硬件平台为：Intel Core i5-6200 CPU 2.4GHz，内存8GB，操作系统Windows10,使用C#在Visual studio2013运行环境中实现三种算法，测试数据集来自http://fimi. uantwerpen.be/data/.如表2所示选取3个不同特点的数据库进行关联分类规则挖掘性能实验.

表2 实验数据库特征

5.1 挖掘时间

实验对比了三种算法挖掘带约束CARs消耗的时间,实验中minconf=50%,约束集β根据属性值的选择率s进行模拟.例如：Pumsb数据库拥有2113不同的属性值，20%选择率约为423个属性值作为数据约束.由图6测试结果可知，随着minsup降低，本文提出算法LD-CAR性能优于改进的CCAR算法与类Apriori的MAC算法，尤其在随着minsup不断变小的过程中，LD-CAR算法时间消耗增加缓慢，尤其在Pumsb这类数据集庞大且稠密的数据集上性能优势更加明显.经试验分析可明显看出，本文引入基于差集的扩展概念格结构后，通过存储差集信息能够快速计算子结点类别支持度，有效提高结点生成效率，关联分类规则提取算法有效压缩了搜索空间，从而加快了算法的收敛速度.

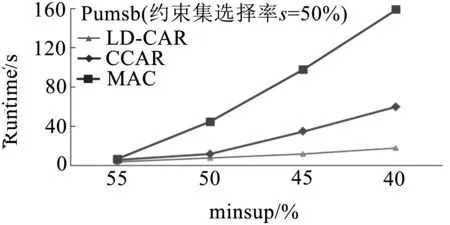
(a) Chess数据库

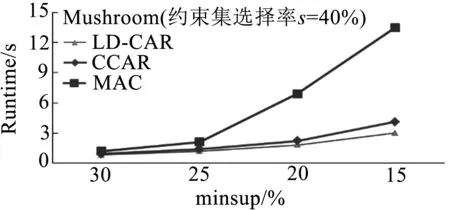
(b) Mushroom数据库

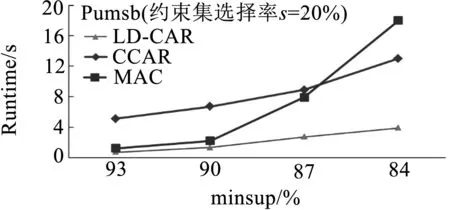
(c)Pumsb数据库图6 扩展概念格二层结点与高层结点计算过程

5.2 内存使用

实验对比了CCAR与本文算法LD-CAR的内存使用情况，内存占用主要取决于算法采用存储结构，CCAR采用树形结构，本文LD-CAR采用基于差集的扩展概念格结构，对比结果如表3所示.可以看出在不同数据库中LD-CAR算法均占用较少内存，尤其在记录数庞大的稠密数据库Chess与Pumsb中，两个项目集链接后的孩子结点仅存储差集信息极大降低了格空间占用.

表3 两种算法内存使用对比

6 结论

本文在深入研究关联分类理论的基础上，提出了一种基于扩展概念格的带约束关联分类挖掘方法. 该方法主要分为两个步骤：扩展概念格的建立和在其上的带约束关联规则提取. 算法设计基于差集的扩展概念格结点结构，根据用户需求引入约束条件控制挖掘方向，并给出了相应格构建算法和在其上的关联分类规则提取算法；该方法优势如下：

(1)设计扩展概念格结构，每个结点中包含全部的频繁项集信息，该结构在不丢失有效信息的前提下降低了建造整个格的复杂度，应用定理可有效缩减了扩展概念格中结点的数目，避免了由于候选项目集结点产生过多导致效率低下问题；

(2)在扩展概念格高层结点结构中引入差集概念，可加快结点链接操作运算时间.高层格结点中存储差集信息代替存储记录集也可有效减少内存占用；

(3)该算法非常适合重用.当约束条件集根据用户需求发生改变时，格无需重新建立，重新挖掘的时间大大减少了,满足重用性要求.

进一步的工作可以考虑将本文算法推广到大数据环境中，研究分布式辅助关联分类，还可以对分类器进行动态调整[12]，使算法挖掘的结果更具参考价值.