一元微积分理论近期发展内容的比较分析
2021-07-28李红玲
李红玲
(宿迁学院 文理学院,江苏 宿迁 223800)
0 引言
微积分体系由牛顿和莱布尼兹于17世纪后期建立起来,后经柯西等科学家不断完善,把不等式从近似方法的一种工具转变为严格理论的工具,将微积分从一个产生成果的有效方法转变为我们今天所熟悉的严格学科,这个逐步完善的过程前后花了约150年的时间[1]。目前,国内外的常见教材[2-10]均达成了一致:导数采用因变量增量与自变量增量比值的极限这一形式进行定义,定积分采用“分割、近似、求和、取极限”的步骤给出,而微积分基本定理利用积分上限函数证明得到。
科学的探究从来不会停下脚步,现在仍然有很多学者在研究一元微积分的基础理论,对导数定义、积分定义和微积分基本定理的证明方法提出不同的观点,不断促进微积分的发展。以导数定义为例,很多研究者试图不使用极限、从初等知识入手去给出直观的定义,以加快微积分的普及;以微积分基本定理为例,有些研究者从图形入手直接给出微积分基本定理,其中定积分的定义只是作为一个副产品,这些新的思路可以给教学提供更多的信息。
本文分别从导数定义与微积分基本定理证明两个方面呈现近期的发展研究,并对它们进行比较分析,以期达到促进微积分教学与普及的目的。
1 导数定义的比较分析
1.1 导数定义研究的几种形式
常见教材中先给出直线运动速度与切线问题这两个引例,然后抽象出函数在一点处导数的定义,以增量比值的极限形式呈现,即
(1)
美国纽约州立大学奥尔巴尼分校RANGE R M教授、广州大学的张景中院士、中国科学院的林群院士以及西北工业大学的沈卫国研究员均给出了不使用极限的定义方式,下面一一阐述之。
1.1.1 RANGE的导数定义[11]
思路:将y-f(a)=m(x-a)看作过点(a,f(a))且斜率为m的直线方程,它与y=f(x)的交点就是方程f(x)-f(a)=m(x-a)的解,这样由f(x)-f(a)=m(x-a)得到的m就是斜率,也就是导数。
定义1若f(x)-f(a)=q(x)(x-a),则f′(a)=q(a)。
1.1.2 张景中的导数定义[12-15]
思路:平均速度总是在该段某两个时刻瞬时速度之间,由此进行抽象。
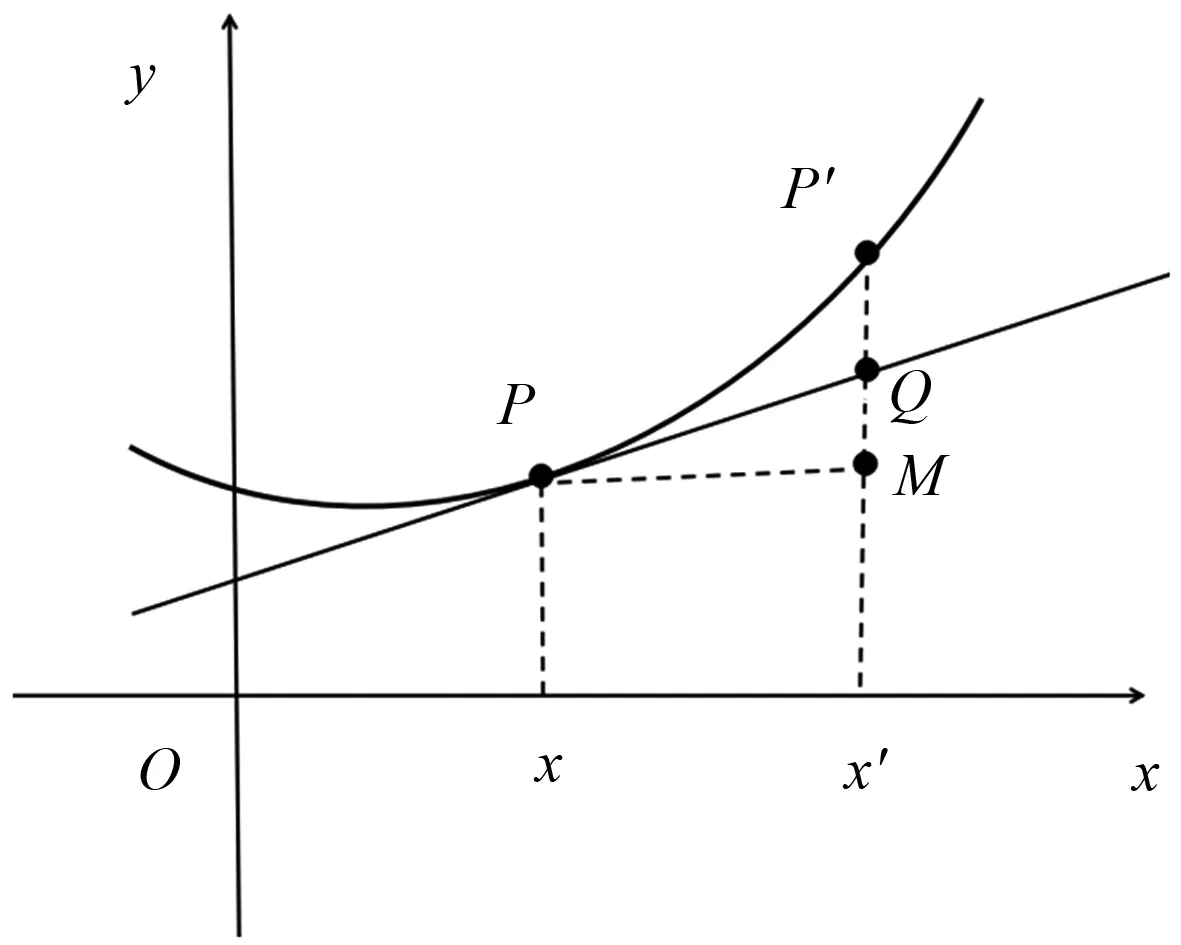
定义2设F(x)和f(x)都在区间I上有定义,若对I中任意两点u 成立,则称f(x)是F(x)的差商控制函数。若有|f(u)-f(v)|≤M|u-v|,其中M为大于零常数,则有f(x)是F(x)的导数。 1.1.3 林群的导数定义[13-15] 思路:由小路程=(瞬时速度+小变化)×短时间 =瞬时速度×短时间+小变化×短时间,得到 f(x+h)-f(x)=g(p)h+εh,则有|f(x+h)-f(x)-g(p)h|≤Ch2。 1.1.4 沈卫国的导数定义[16] 思路:把曲线方程看作过该曲线上任意两点的割线方程,则Δy/Δx不仅可以看作曲线增量与自变量增量之比,还可以看作割线增量与自变量增量之比,这样采用不同的符号表示,先令Δg=1,再令Δx=0,从而得到结果(图1)。 图1 沈卫国导数定义Fig.1 Derivative definition by SHEN Weiguo 1.2.1 共同点 4种导数定义均没有使用极限,也都避开了0/0的情形,使用等式或不等式呈现运算主体,通过定义其中的一部分为导数直接得到结果。背景分为两种:“直线斜率”的几何背景与“瞬间速度”的物理背景,其本质相同。虽然有的研究是为了简化常规微积分,有的是为了纠正0/0的误区[16],但是总的来说,这4种均使用了直观形象的方法将导数的定义引出。 1.2.2 不同点 首先,应用的简洁性不同,通过两个例子进行对比。 由此可见,应用的简洁性影响着方法的普及率,若定义形式直观形象且应用简洁,读者就易于接受,该方法就易于推广。通过对两个简单的幂函数求导的例子可以看出RANGE的导数定义使用起来最为简洁。 其次,适用范围不同。RANGE的导数理论仅适用于多项式函数;而后三者的导数理论可以适用于初等函数范畴。从条件来看,张景中要求导函数满足李普希兹条件,而林群要求函数满足小尾巴绝对值小于等于C|h|,其本质均为一致可导性,而其他导数理论均采用点可导。一致可导体现的是函数在整个区间上的一种特性,而点可导是函数在一点处的特性,也就是说,前者是整体性质,后者是局部性质,由一致可导可以推出点可导[17]。相比较而言,前三者的理论内容较全面,如张景中还利用差商控制函数进行了函数的近似值、增减性与凸性等方面的探究[14],而沈卫国的理论呈现内容有限,很多细节还有待进一步的完善。但是不得不说的是,虽然张景中、林群、沈卫国均表示可以将导数定义应用到幂级数之外的其他初等函数上,但是求解时均比较复杂,比常见教材中求导数要复杂,不具备简便优势,因此这些新理论的关注点在于降低定义难度、促进读者对导数定义的理解,以期达到易懂易普及的目的。 2.1 微积分基本定理证明过程的几种形式 (2) 美国纽约州立大学奥尔巴尼分校RANGE R M教授、美国科学院院士LAX P、广州大学的张景中院士和清华大学萧树铁教授均给出了不同的证明方式,下面逐一阐述。 2.1.1 RANGE的证明[11] 证明由微分中值定理,有F(x+h)-F(x)=F′(c(x,h))h,其中c(x,h)在x与x+h之间。 再由微分中值定理,且要求|F″(x)|≤M,有 |F′(c(x,h))-F′(x)|=|F″(ξ)(c(x,h)-x)|≤M|c(x,h)-x|≤M|h|, (3) 由不等式(2)、(3)得到 |F(x+h)-F(x)-F′(x)h|=|F′(c(x,h))h-F′(x)h|≤M|h|2, (4) 将[a,b]分段,得到 (5) 则当h→0时,有 (6) 2.1.2 LAX的证明[17-18] 证明设a=a0 (7) 则有 F′(ti)(ai-ai-1)=F(ai)-F(ai-1), (8) 累加得 (9) 2.1.3 张景中的证明[12-15] (10) 2.1.4 萧树铁的证明[19] F(a+h)-F(a)=f(a)h+o1(h), (11) F(a+2h)-F(a+h)=f(a+h)h+o2(h), (12) … F(a+kh)-F(a+(k-1)h)=f(a+(k-1)h)h+ok(h), (13) … F(b)-F(b-h)=f(b-h)h+on(h)。 (14) 把(11)~(14)式及省略的式子两边相加,左端消去中间各项,最后得到 (15) 或 (16) 取极限得 (17) 2.2 4种微积分基本定理证明过程的比较分析 2.2.1 定积分的出现顺序与定义方式不同 LAX先定义了定积分再给出微积分基本定理的证明,而RANGE、张景中、萧树铁均是在推导微积分基本定理的过程中顺带给出定积分定义;LAX、RANGE和萧树铁的定积分均由“分割、求和、取极限”步骤得到,而张景中却是将曲边梯形的面积直接定义为定积分。且定义过程中“任意性”不同:常见教材定积分定义中存在两个“任意”:一是对线段的分割是任意的,这对应着小曲边四边形的面积具有任意性;二是在每个小区间[xk,xk+1]上取点ξk是任意的,这对应着小矩形的高f(ξk)具有任意性RANGE采用了对线段进行平均分割的方式;萧树铁的定义中不存在这两个任意:一是对线段采用平均分割;二是小区间上取点均采用左端点f(a+kh)(k=0,1,2,…,n-1)。 那么定积分定义中“两个任意性”是否可以修改?只用“平均分割”是否会导致定义的不严谨?RANGE与萧树铁都用了平均分割,无独有偶,加拿大史迪沃特的微积分教材中也采用了平均分割[9]。其实,研究早已表明,定积分中两个任意性的作用:反映客观量的客观属性以及提供计算积分的灵活性。但实际上,两个任意性只有一个在起作用,可以通过对特殊划分任意取点完成,也可以通过任意划分特殊取点完成[20]。因此,使用“平均分割”并不影响定义的严谨性。 2.2.2 定理证明的前提条件不同 2.2.3 定理证明方法不同 2.2.4 证明过程的接受效果不同 由于LAX已经给出了定积分定义,因此其证明过程比较容易接受一些;张景中的证明偏直观,在张景中与林群的合作文献[14]中,利用“余弦面积正弦高”这一特例简单直观地给出微积分基本定理的思想,再从特殊到一般,给出定理的证明过程,过程中直接将面积定义为定积分,根据几何关系得出了等式,文献[12]中还有存在性的证明;而RANGE和萧树铁事先并没有定义定积分,因此证明过程的几何理解比较困难。如萧树铁的证明过程中存在着几处会让读者疑惑的细节:首先,该教材中对微分的定义是从几何图形出发(图2),利用“以直代曲”的思想,用线性函数的值代替函数值,得到 图2 微分定义Fig.2 Definition of differential f(x+h)=f(x)+MQ+QP′=f(x)+f′(x)h+o(h), (18) 图3 定积分定义Fig.3 Definition of definite integral


1.2 4种导数定义的比较分析


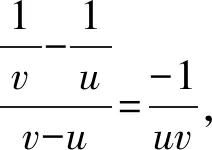




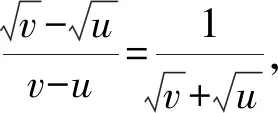


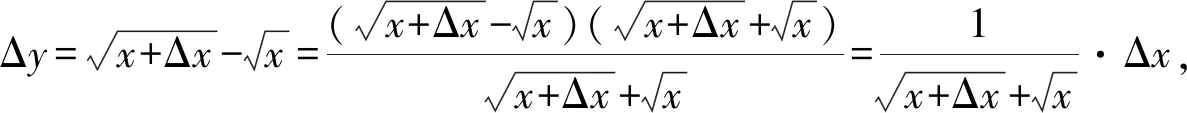
2 微积分基本定理证明过程的比较分析
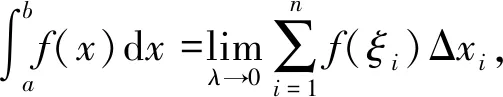

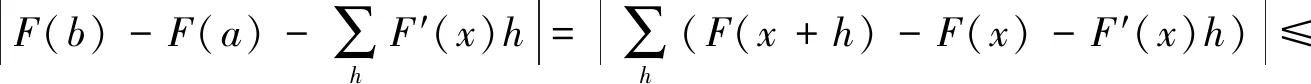

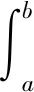

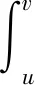
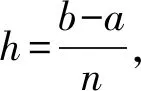
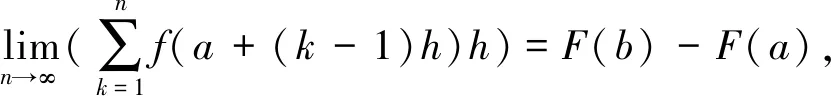
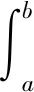
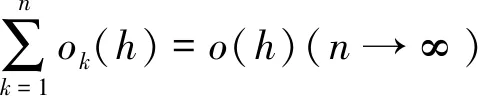
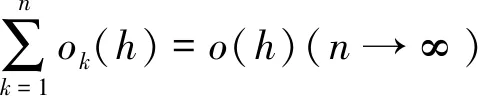


3 思考与建议

