一类随机泛函微分方程的μ伪概自守解
2021-07-28朱平
朱 平
(洛阳师范学院 数学科学学院,河南 洛阳 471934)
0 引言
在描述随机动力系统时,带有时滞的随机微分方程更能精确地刻画相应的动力学性质[1-2]。 此外,自概自守随机过程提出以来,越来越多的学者对该过程进行深入研究并应用到随机微分方程[3-6]。 作为概自守随机过程的推广之一,μ伪概自守随机过程由DIOP M A等提出[7],并研究其复合定理和空间完备性。到目前为止,μ伪概自守随机过程在随机泛函微分方程中的研究甚少,尤其是中立型随机微分方程。为使μ伪概自守随机过程的应用更广,本文研究如下一类由Brown运动驱动的带有μ伪概自守系数的非线性随机泛函微分方程
(1)
在合适的条件下,证明该随机微分方程存在唯一的p次μ伪概自守温和解。该结论的研究进一步丰富了μ伪概自守随机过程的复杂动力学,因此,本文的研究有重要的理论意义和价值。
1 基本知识
令(Ω,F,P)是完备的概率空间,其滤子为{Ft}t≥0。 令W(t)是Q-Wiener过程,对一个Banach空间(H,‖·‖)和p≥1,用B=B((-∞,T],H)表示范数‖·‖B的完备空间,且对任意的X∈B,有Xt=X(t+·)∈B。此外,用Lp(P,H)表示所有H值的随机变量X构成的集合,满足
设A:D(A)→H是解析半群{T(t)}t≥0的无穷小生成元,则对β>0(A-βI)是可逆的。 假设0∈ρ(A),其中ρ(A)是A的预解集。进而,可在定义域D((-A)β)上定义闭线性算子(-A)β,且对t>0,λ>0有‖(-A)βT(t)‖≤Mβt-βe-λt。
令B1是R上所有的Lebesgueσ-域构成的集合,M是B1上所有的正测度μ构成的全体,满足μ(R)=+∞且μ([a,b])<+∞,对a,b∈R。此外,设
H0对所有的τ∈R,记μτ(A)=μ(a+τ:a∈A),A∈B1,则存在α>0和有界区间I满足
μτ(A)≤αμ(A),
其中A与I无交集。
下面介绍一些定义和引理。
定义1[7]令μ∈M,称随机过程X是p次μ遍历的,如果
记所有这种随机过程的集合为PAA0(R,Lp(P,H),μ)。
引理1[7]令μ∈M满足H0,则PAA0(R,Lp(P,H),μ)是平移不变的。
定义2[7]称随机过程X:R→Lp(P,H)是p次μ伪概自守的,如果X=X1+X2,其中X1是p次概自守的即X1∈AA(R,Lp(P,H))且X2∈PAA0(R,Lp(P,H),μ)。记所有这种随机过程构成的集合为PAA(R,Lp(P,H),μ)。在上范数‖·‖∞下,对μ∈M是Banach空间。
2 存在唯一性
在介绍本节主要结论之前,先给出以下假设。
H1存在正常数M0和δ满足
‖T(t-s)‖≤M0e-δ(t-s)。
H2g∈PAA(R×Lp(P,H)×B,Lp(P,Hβ),μ),对任意的t∈R,y,y1∈B以及x,x1∈Lp(P,H),有
H3h∈PAA(R×Lp(P,H)×B,L(P,Lp(P,H)),μ),对任意的t∈R,y,y1∈B以及x,x1∈Lp(P,H),有
定义3称Ft-适应的随机过程x(t)是随机微分方程(1)的温和解,若
定理1令H1~H3成立,若
(2)
则随机微分方程(1)存在唯一的μ伪概自守温和解。
证明对任意的x∈PAA(R,Lp(P,H),μ),定义算子Φ为
(Φx)(t)=T(t)[x(0)-g(0,φ(0),φ)]+g(t,x(t),xt)+
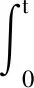
在条件H2和H3下,不难证明g(t,x(t),xt)和h(t,x(t),xt)是μ伪概自守的随机过程,从而可推出T(t)[x(0)-g(0,φ(0),φ)]是μ伪概自守的。根据定义2可知,存在随机过程g1,h1∈AA(R,Lp(P,H))以及g2,h2∈PAA0(R,Lp(P,H),μ),使得g=g1+g2并且h=h1+h2。 因此Φ(t)=g(t,x(t),xt)+Φg1,h1(t)+Φg2,h2(t),其中
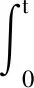
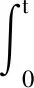
下面分两步进行证明。
第1步算子Φ是定义在空间PAA(R,Lp(P,H),μ)上的自映射。
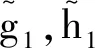
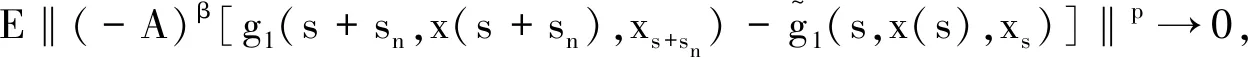
(3)
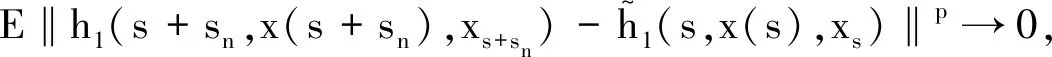
(4)
利用Hölder不等式以及Burkholder-Davis-Gundy不等式,得

利用(3)、(4)和Lebesgue控制收敛定理, 则



因为g2,h2∈PAA0(R,Lp(P,H),μ),利用引理1可得
利用Lebesgue控制收敛定理,则有(Φg2,h2x)(t)∈PAA0(R,Lp(P,H),μ)。 进一步,可推出(Φx)(t)∈PAA(R,Lp(P,H),μ)。
第2步算子Φ是压缩映射。
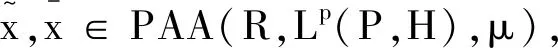
利用(2),则
根据第一步和第二步的证明,利用Banach不动点定理可得随机微分方程(1)存在唯一的μ伪概自守温和解。
定理2令H1~H3成立,若
(5)
则随机微分方程(1)存在唯一的全局指数稳定的μ伪概自守温和解。
证明由定理1可知,在条件(5)下,随机微分方程(1)存在唯一的μ伪概自守温和解x*。进而,假设x是方程(1)任意的温和解,则
在条件H1~H3下,计算得
在条件(5)下,存在ε∈(0,δ)使得η<1,其中
对任意的T0>0,可得下列积分
即
因为ε∈(0,δ)且η<1,故当t→+∞时,有
eεtE‖x(t)-x*(t)‖p→0,
即x*是全局指数稳定的。
