冻结砂土层中埋地管道管土界面应力分析

王一民,王凯勃，徐 艳，王尊策,卢召红

(1.东北石油大学，黑龙江大庆 163318;2.中国石油 大庆石化分公司，黑龙江大庆 163714)

0 引言

寒区埋地管道由于气温长时间处于0 ℃以下，会导致埋地管道周围的土体发生冻胀现象，此时管道与土体之间的力学性能就会发生改变，严重时可能会对管道输送的安全产生不利影响[1]。因此，研究冻土地带管道与土体之间的界面应力问题，可以为保障管道运输的安全提供理论支撑。

埋地管道与土体间的相互作用一直以来被众多学者所关注。黄龙等[2]归纳了冻土区管道工程的研究现状及发展过程，总结了室内外管土相互作用的相关试验、数值模拟分析和理论分析方法。刘全林等[3]建立了管土相互作用的弹性组合模型，得出管-土接触面上不仅有正应力还有剪应力，同时考虑埋地管道埋设条件、回填介质对管土相互作用的影响，建立了管土相互作用平面问题的传递矩阵分析法。在此基础上，张坤勇等[4]考虑开挖引起的地层位移对地下管线应力和变形的影响，建立了任意载荷条件下管线的理论公式，将理论计算结果与有限元分析计算结果进行了比较，验证了解析方法的可靠性。张海丰等[5]针对埋地管道周围土压力分布规律、管道内部应力特征、管道破坏机理以及填土对管道受力状态的影响等，利用土箱模型试验研究了上述因素下的管土相互作用问题。QIN等[6]通过管土相互作用数值分析模型，利用平面应变抗剪强度参数表征了数值模型中的回填砂，考虑弹性模量随深度的变化关系，得出了一种新的关于应力-位移曲线的本构模型。

本文根据上述研究，采用双线性界面内聚力有限元分析模型，建立冻结砂土与管道相互作用分析模型，研究冻土与管体轴向载荷作用下的界面应力问题，通过试验验证有限元分析模型的可靠性，为进一步研究埋地管道局部损失、腐蚀坑应力集中致损问题奠定基础。

1 管土层间界面切向应力位移本构试验

1.1 试验概况

试验主要研究确定冻结砂土的基本物理性能和冰冻条件下砂土与埋地管道间的界面应力[7-8]。试验设备包括JPW-10型电液伺服加载装置系统、数据采集系统、标准型ELDyn冻土动静三轴测试系统和自制试验土箱等。

试验土箱模型尺寸为：1 000 mm×580 mm×600 mm(长×宽×高)，土箱由10层40 mm×40 mm方钢管组成，采用螺栓连接每层方钢管，相邻两层槽钢间隙为20 mm。采用3 mm厚钢板焊于土箱底部和前后两侧作为土箱挡板。前后挡板中间预留一直径为40 mm的管道安装孔。模型尺寸和管径均满足几何尺寸相似关系，同时考虑了试验土箱模型尺寸受试验装置、土壤质量和管道模型尺寸等因素的影响。

加载装置的水平载荷作用于管道的自由端，加载方式为位移控制，加载速率为0.05 mm/s，当加载点一端的管土界面力趋于稳定时，载荷终止，即加载端产生管土分离现象。试验得出的结果可根据相似关系，应用到实际工程中的大管径问题。试验装置及试件实物图和结构见图1。

(a)试验装置及试件

(b)试验土箱与试件结构示意图1 试验装置及试件实物图与结构示意Fig.1 The actual photo and schematic diagram ofthe test device and specimen

1.2 冻结砂土基本物理参数测定

为了得到冻结砂土的基本物理参数，制作了3个标准冻结砂土样本测试，以确定冻结砂土的物理性质。砂土颗粒级配图如图2所示。

图2 砂土颗粒级配图Fig.2 Sand particle grading map

制备含水率为7%的试验土样，采用环刀法，根据式(1)和式(2)计算土样的干密度。

ρo=mo/V

(1)

式中，ρo为土样的湿密度,g/cm3；mo为土样的质量,g；V为土样的体积,m3。

(2)

式中，ρd为土样的干密度,g/cm3;wo为土样的含水率,%。

非饱和状态下砂土在-18～-20 ℃冬季寒冷环境下冻结24 h，通过无限压缩试验测定了土样的压缩特性，测量的应力-应变曲线如图3所示。分别在100,200,300 kPa三种围压下对试验土样进行三轴剪切试验，每种围压下试件做3组试验取其平均值，冻结砂土试验土样剪切应力-位移曲线如图4所示。采用三轴压缩试验测得土样的粘聚力和内摩擦角，三轴测试系统见图5。试验测定各土样基本物理参数平均值如表1所示。

图3 冻结砂土试验土样应力-应变曲线Fig.3 Compression stress-strain curve of frozensand soil sample

图4 冻结砂土试验土样剪切应力-位移曲线Fig.4 Shear stress-strain curves of the frozensoil samples

图5 标准型ELDyn冻土动静三轴测试系统Fig.5 Standard ELDyn frozen soil dynamic andstatic triaxial test system

表1 土样的基本物理参数Tab.1 Basic physical parameters of soil samples

根据图3,4所示的试验结果，冻结砂土的动弹性模量可用式(3)计算：

(3)

式中,ECS为冻结砂土的动弹性模量,MPa；σCS为压应力,MPa；εCS为压应变。

1.3 管道力学性能参数

试验截取了3根长度相同、使用状况相同的钢管，并对3次试验结果取平均值。管道材料基本力学性能如表2所示，为尽可能模拟实际工程中管道处于冻结砂土中的状态，将管道埋置在靠近土箱模型中间位置，以减小土箱壁对于试验结果的影响，减小误差，故管道中心埋置深度为300 mm，管道直径D小于0.1倍的埋置深度。沿管道轴向均匀布置5个应变片，应变片的间距为210 mm，标号分别为Y1,Y2,Y3,Y4,Y5，如图6所示，采用全桥式应变片粘贴方式。使用数据采集装置采集试验管道的应力、应变值。

表2 管道主要材料性能参数Tab.2 Material performance parameters of the pipe

图6 应变片布置示意Fig.6 Schematic diagram of strain gauge layout

1.4 试验结果与分析

根据冻结砂土层中管土相互作用试验得出的数据，用差值法计算得到管土界面剪应力-位移关系曲线，计算方法如式(4)～(7)所示。

τ=V/A

(4)

式中，V为两测点间的剪切力,MPa，V等于试验管道在两个相邻测点间所受的拉力差值，即V=∣Ti-Ti+1∣；A为相邻测点间的管土接触面积,mm2。

V=∣εi-εi+1∣Ed2πR

(5)

式中，εi,εi+1分别为相邻两测点试验管道表面应变值；E为试验管道的弹性模量；d为试验管道壁厚,mm；R为试验管道外径,mm。

A=(li+1-li)2πR

(6)

式中，li,li+1分别为相邻两测点至Y1的距离,mm。

τ=ΔεEd/Δl

(7)

经过对采集数据进行分析，发现Y4，Y5两测点的结果比较稳定，利用Y4，Y5对应的应变值，按式(7)计算出管土间的界面剪应力，绘制管土界面剪应力-位移曲线，如图7所示。

图7示出在冻结砂土层中，管道受轴向拉力作用时，曲线分为三个阶段。首先管土界面处的剪应力随管道变形增大而增大；达到极限应力后，管土相互脱离，界面剪应力骤减；管土继续发生相对位移，管道与土体间的冻结力与粘聚力影响逐渐减小，管道与土体之间的滑动摩擦力逐渐占据主导地位，此时曲线慢慢趋于平缓，由于此阶段对于研究管土之间界面应力影响较小，可忽略此阶段。冻结砂土中管土界面处的最大界面剪应力为392.9 kPa，此时管道变形值为57.3 mm，达到极限应力后界面剪应力减小至203.4 kPa，随后趋于平缓，管土相对位移增大至77.4 mm。管道受冻胀影响，会使管道局部抬升，由于抬升处左右两侧界面应力过大，会使管道在抬升处应力集中过大，从而发生管道破坏事故。

图7 冻结砂土中管土界面剪应力-位移曲线Fig.7 Shear stress-displacement curve of pipe-soilinterface in frozen sand

2 管土层间界面应力有限元分析

2.1 基本假定

在建立冻结砂土与埋地管道相互作用有限元分析模型时，采用如下基本假定：(1)冻土是一个小的弹性空间体，管道与周围土壤之间的界面位于空间的无弯曲表面;(2)根据图7所示的试验结果，可假定管土界面剪应力-位移关系为双线性本构关系，管道与冻结砂土之间的界面应力完全符合管土界面应力的分析模型。

2.2 模型建立

借助ABAQUS有限元分析软件，建立有限元分析模型[9-10]，土体和管线均采用C3D8R单元建立，模型大小与试验中的一致。土体采用摩尔-库伦塑性赋予粘聚力和内摩擦角度[11]，材料本构关系采用试验研究部分测定的数据。利用有限元软件中的初始边界条件将土体三面固定，土体与管道之间的相互作用[12]采用基本假定第二条中的双线性剪应力-位移关系来表征其本构关系。在有限元分析软件中，双线性内聚力模型[13-14]是广泛采用的一种本构关系模型，界面粘结力在外载荷作用下，初始剪应力与位移呈线弹性变化关系，应力达到最大值τm后，界面出现损伤并不断扩展，剪应力-位移关系进入线性软化阶段，直至最终完全脱离失效，其具体形状如图8所示。其切向T-S关系控制方程如下:

图8 双线性界面剪应力-位移关系模型Fig.8 Bilinear interface shear stress-displacementrelationship model

(8)

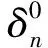
2.3 有限元结果与分析

在ABAQUS模拟软件中得到应力云图如图9所示。将试验与有限元分析结果作对比分析，如图10所示，试验值与有限元分析值基本吻合。

图10示出埋地管道管土界面应力-位移关系。有限元分析模型取土的弹性模量为常数，界面应力与相对位移两者之间是线性关系，此时可以认为冻土在一个小变形范围内为弹性体，试验结果与有限元分析结果误差为3.97%，两者结果基本吻合。由于在有限元模拟时管土的相互作用本构模型采用的是双线性内聚应力-分离位移关系模型，该模型认为界面应力在达到峰值后一直下降直至消失，所以有限元曲线相较于试验曲线无水平段。而实际试验中管土完全脱离之后，管土之间的相互作用变为滑动摩擦，所以试验曲线中有近似水平段出现，并且冻结砂土的动弹性模量ECS受温度、围压、密实度等因素的影响较大[15-16]，而有限元分析模型并未考虑这些因素，导致试验值与理论值有一定误差。

(b) 管道应力云图图9 管土相互作用有限元分析结果Fig.9 Finite element analysis results ofpipe-soil interaction

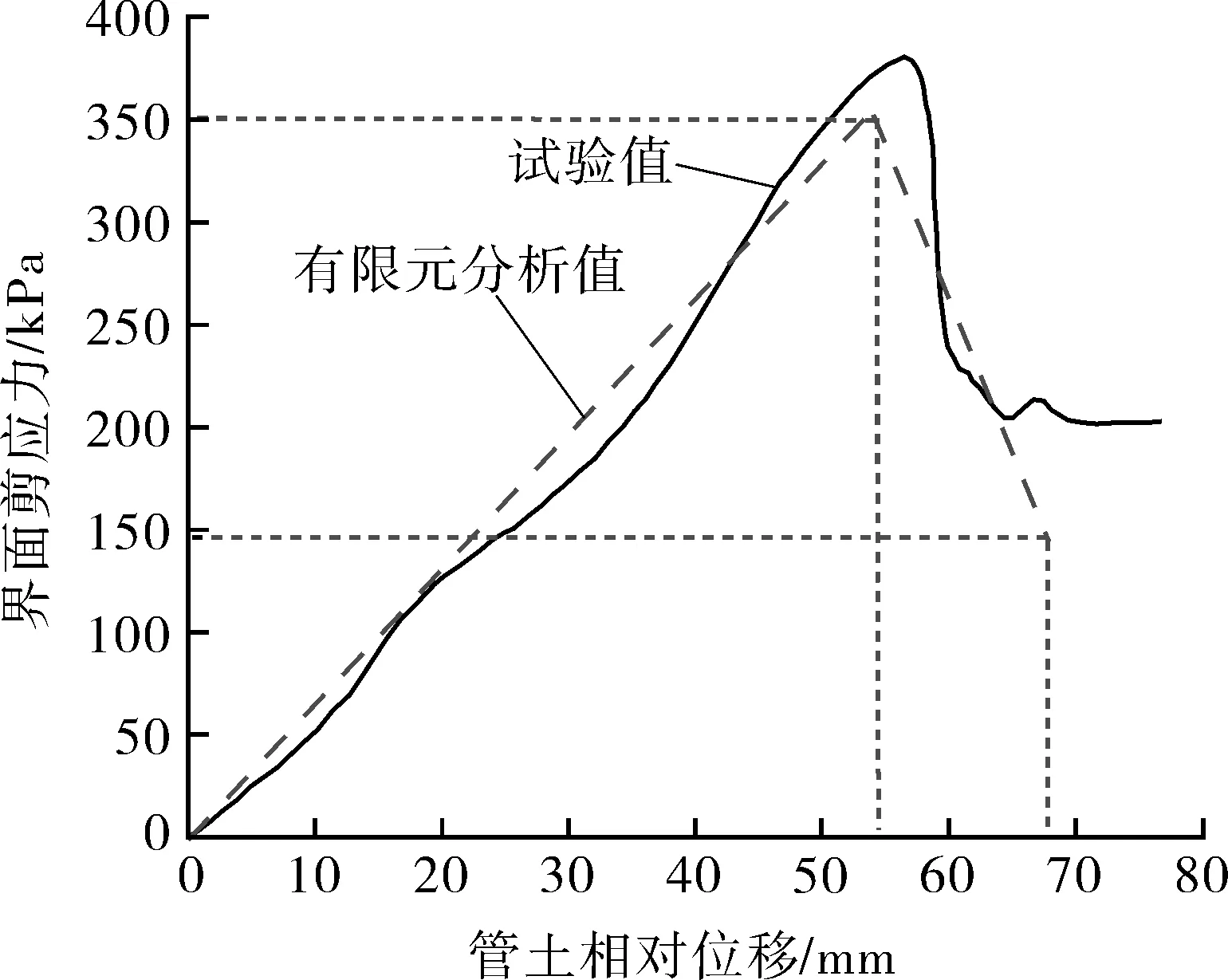
图10 埋地管道管土界面剪应力-位移关系Fig.10 Shear stress-displacement relationship ofpipe-soil interface of buried pipeline

实际试验中由于试验条件的限制和人为条件的影响，试验得出的曲线并不是两条直线，但总体趋势呈双线性。本文采用有限元方法建立的双线性粘聚模型与试验值的误差小于5%，在工程误差允许范围之内，为进一步研究埋地管道局部损失、腐蚀坑应力集中致损问题奠定基础。未来在本模型基础上还可进行冻结砂土层中埋地管道在复杂应力场条件下的管土界面应力作用分析，例如在地震或其他外力作用下引起的管道变形与位移，研究此时的管土界面应力也可为寒区管道运输的设计与防灾减灾提供理论依据。

3 结论

(1)根据冻结砂土层中管土相互作用试验，管土界面剪应力-位移关系曲线可以简化为两个阶段，由此建立了双线性管土间界面剪应力-位移本构模型。

(2)根据双线性管土界面剪应力-位移本构模型，建立了冻结砂土与埋地管道界面应力有限元分析模型，研究了冻土层中埋地管道管土的相互作用。将有限元分析结果与试验结果进行对比分析，验证了有限元模型的准确性。因此该有限元分析方法可用于计算寒区冻土层埋地管道在轴向剪切力作用下的管土界面应力。

(3)通过对试验、理论和有限元模拟分析得出的曲线进行比较，发现这3种曲线趋势一致。因此假定冻土是一个弹性较小的空间体，管道与周围土壤之间的界面位于空间的无弯曲表面是合理的，同时也证明本文建立的双线性管土间界面剪应力-位移本构模型是正确的。

(4)建立的有限元模型用于模拟计算冻结砂土内管-土之间的轴向界面应力，有限元分析结果与试验结果的误差为3.97%，较为吻合。由于管土相互作用本构模型与实际管土接触情况略有差异且冻结砂土的动弹性模量受围压、密实度等因素的影响较大，而有限元模型中未考虑这些因素，这是误差产生的主要原因。