小学数学解决问题的方法和策略

汪自萍

摘 要：小学生的思维处于具体形象思维向抽象逻辑思维的过渡阶段，在解决复杂的数学问题时，可通过画线段图、画图表、数形结合等方法帮助学生建立解决问题的模型，从而使复杂的数学问题简单化，提高小学生解决数学问题的能力。

关键词：画图;方法;解决问题

数学是一门逻辑性很强的学科，同时又是较抽象的学科。小学生以形象思维为主，为了帮助学生真正理解数学知识，我在日常教学过程中注重数学知识与学生生活经验的联系、与学生学科知识的联系，组织学生开展实验、操作、尝试等活动，引导学生进行观察、分析，把所学知识化繁为简，引导学生理清数学本质及其体现的数学思想，帮助学生理清相关知识之间的区别和联系等。

一、术有专攻，巧用“画图”策略解决数学“瓶颈”问题

如在教学第二册“求一个数比另一个数多几（少几）”的解决问题时，一年级的小学生容易犯见“多”就加、见“少”就减的毛病。这反映了学生不是通过分析数量关系解决实际问题，而是凭题目中“多几”“少几”等字词机械地决定用加法、减法。长此以往，会让学生形成思维的惰性，阻碍学生的智力发展。教师如果口头讲解，也很难说清其中的数量关系，如果利用画图，能直观形象地呈现出其中的数量关系。我在教学过程中，引导学生弄清“谁与谁比”“谁比谁多多少（或少多少）”，真正理解“甲比乙多几”就是“乙比甲少几”。

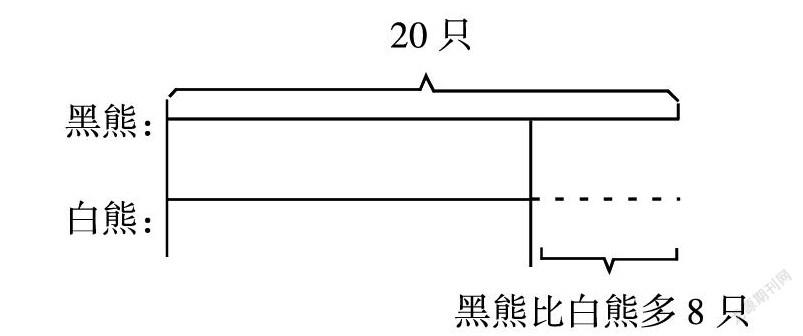
例如：动物园有20只黑熊，黑熊比白熊多8只，白熊有几只？

指导学生根据题意画出白熊的线段图，理解关键词“黑熊比白熊多”，就是“白熊比黑熊少”，白熊的线段图就要画得短一些。

画图时先确定一个量，再根据数量关系的关键词画出另一个量，根据图形表示的数量关系解决问题。帮助学生找到一些关键词语，谁比谁长多少（或短多少）;谁比谁高多少（或矮多少）;谁比谁贵多少（或便宜多少）……直观地将题目中的条件和问题表示出来，明确思维方向。

二、冲云破雾，发散学生的数学思维

变通，是发散思维的显著标志。学生在解决问题时，由于思维的出发点、思维的方向或思维的方法不对，容易步入死胡同。教师巧用绘图可以开拓学生的解题思路，展开思考过程，使学生茅塞顿开。在教学活动中，教师要善于引导学生尝试用画图的方法来理解复杂的数量关系和题意，这样既能锻炼学生的思维，更能促进他们思维能力的提升。我利用图形结合帮助学生分析、理解数量关系，解决实际问题。

在平时的教学过程中我利用转化思想，帮助学生理清思路，回忆和寻找解决问题的途径和策略，发现问题中可能存在的关系，创造各种机会，让学生自觉产生画图的需求，体验画图策略在解决问题中的价值，利用线段图帮助学生把倍数关系转化成分数关系，可以促进学生对问题的理解和把握。

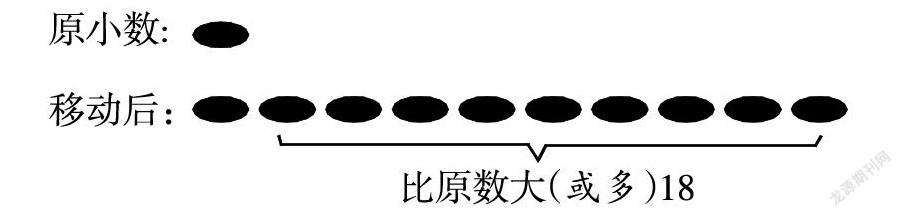
例如：一个数的小数点向右移动一位后，比原数大18，原数是多少？

在教学这一题时我引导学生把它转化成倍数关系的解决问题，找到关键詞向“右”移动一位，就是小数扩大10倍，用图表示是：

要理解其中的关键，移动后的小数是原小数的10倍，也就比原小数多9倍，这9倍是18。

在数学教学中，我充分引导学生用不同形式的图解决不同的数学问题;引导学生根据不同的问题，选择合适的图形来解决问题。

总之，学生在具体的实践操作过程中，选择运用认为最能帮助自己分析和解决问题的图来明白题意，理清数量关系，解决实际问题。教师的教学不仅要教给学生知识，更重要的是教给学生学习知识的方法，帮助学生轻松、愉快地学会解答复杂关系的问题，在画图的过程中既培养了学生的能力，又促进了学生思维的发展，让学生都能感受到解决问题的魅力所在，教学效果将会事半功倍，让我们的数学教学充满童真童趣。画图就像一盏明灯，引领我们到达知识的彼岸。

参考文献：

蒋巧君.数形结合是促进学生意义建构的小策略[J].小学数学教师，2006（4）.