GSC结构相控阵在主瓣干扰下的自适应单脉冲方法
2021-07-27陈子昂杨嘉伟陶琛琛
陈子昂, 杨嘉伟, 陶琛琛
(1.北京遥感设备研究所, 北京 100854; 2.中国航天科工防御技术研究院, 北京 100854)
0 引 言
单脉冲技术通过合成的和、差通道的幅度(相位)之比实现对目标角度的估计,拥有简单可靠、运算量少等优点,在雷达、导引和测控等中有着广泛的应用[1]。随着对复杂电磁干扰环境下雷达性能的进一步需求,结合自适应波束合成技术的自适应单脉冲测角技术也油然而生[2]。当电磁干扰源从旁瓣进入时,自适应单脉冲技术能保证和差波束在干扰方向形成抑制的同时保持主瓣测角范围内单脉冲比不变,即在旁瓣干扰环境中能保证测角精度[3],然而当干扰从主瓣进入时,一般的自适应算法会令单脉冲比曲线发生变化,导致测角错误[4]。
为解决主瓣干扰环境下自适应单脉冲测角中出现的问题,国内外学者进行了众多研究。目前有效的算法主要分为两大类,一类是通过阻塞矩阵对接收信号进行预处理,消除主瓣内的干扰信号,然后再利用处理后的信号进行自适应单脉冲测角[5]。然而这类算法存在较多弊端,一是需要知道精确的主瓣干扰方向,二是会减少阵列自由度,变更阵列流型,三是在二维面阵下的干扰阻塞效果不理想。第二类算法的思路是在抑制干扰的同时保持单脉冲比不变,从而提高干扰环境下的测角精度。其中按处理方式的不同又可以分为两种类型,其一是Fante所提出的线性约束法[6],包括Rao等人提出的多点线性约束法[7],以及文献[8]中对平面相控阵和子阵级的线性约束法,通过对差波束进行单脉冲曲线的线性约束,维持了单脉冲比曲线的形状。这种方式对线形阵列在主瓣干扰下测角性能有很大的提高,然而在二维平面阵下仍存在较大的局限性。二维平面阵在测角范围内的两个方向的单脉冲比都是接近于一个平面,为了约束单脉冲比的测角平面一致,差波束需要9个或更多自由度进行约束,因此需要设计更多的通道数来提高自适应算法的性能,而更多的通道数意味更大的计算量,在许多环境下难以满足工程上所需的实时性要求。而且对于旁瓣对消结构的相控阵来说,对差波束进行动态约束是不可行的。另一种类型则是Kai提出一种利用二维平面四通道的输出,在一个方向进行主瓣干扰对消,而保持另一个方向上的单脉冲比不变的方式[9],实现了对两个方向上的精确测角,胡航等人又将该方式应用在子阵中[10]。这种方式不需要消耗更多的自由度,能有效地保证自适应算法的性能,然而目前这类算法仍存在如何优先消除旁瓣干扰,且保证主瓣内的信号和干扰不受到影响的难点问题。
为了解决相控阵雷达在主瓣干扰情况下的单脉冲测角问题,本文在文献[9]的基础上提出了一种在广义旁瓣对消器(general sidelobe canceller, GSC)结构下两级自适应单脉冲测角方式。首先通过特征投影与协方差矩阵重构的方式[11-14],利用旁瓣对消器抑制和差波束中的旁瓣干扰并保持主瓣内信号和干扰不变,再使用四通道主瓣对消器,在俯仰(方位)向形成对主瓣干扰的抑制,并保持方位(俯仰)向单脉冲比不变,达到抑制干扰的同时保证较高的测角精度的效果。本方法不需要对干扰来波方向进行预估计,也不会造成阵列自由度的损失,具有较强的鲁棒性,便于工程实现,最后对本文所提的方法在GSC结构相控阵雷达模型下进行了仿真,并采用工程常用的线性调频信号进行了验证。
1 基于GSC的单脉冲测角模型
考虑到一个由M×N个单元组成的二维平面相控阵,假设空间中存在L+1个远场平面波信号入射到天线阵面,其中包含1个期望信号和L个干扰信号,且各个信号之间互不相关。则经过图1所示GSC后输出的和通道信号为

图1 GSC结构
(1)
式中:wqΣ和waΣ分别为主通道和辅助通道加权系数;MΣ为和通道的阻塞矩阵;x(t)为阵列输出信号,由接收信号和噪声组成,可表示为
(2)
式中:(φ0,θ0),(φl,θl)分别表示目标和干扰的来波方向;s(t)和jl(t)表示信号包络;n(t)表示高斯白噪声;a(φ,θ)是阵列的导向矢量。
当波束指向为(φ0,θ0)时,主通道的加权向量为
wqΣ=a(φ0,θ0)
(3)
阻塞矩阵满足
MΣ×wqΣ=0
(4)
则根据最小均方误差准则,辅助通道自适应权重系数为
(5)
式中:Rx表示信号的自相关矩阵。此时最终的阵列自适应权重系数可以表示为
wΣ=wqΣ-MΣwaΣ
(6)
差波束的自适应权重系数以同样的方式计算,表示如下:
(7)
式中:ΔA,ΔE,ΔΔ分别表示方位差、俯仰差和双差。自适应后输出的信号对旁瓣干扰进行抑制,处理后的方位向和俯仰向的单脉冲鉴角曲面为
(8)
当干扰从旁瓣进入时,自适应方向图在干扰处形成零陷,而主瓣范围内的方向图形状保持不变,此时鉴角曲面变化很小,不会影响测角精度[15]。然而,当干扰进入主瓣时,自适应处理后在主瓣干扰方向上的零陷会令主瓣范围的方向图形状发生畸变,导致鉴角曲面发生很大的变化,引发较大的测角误差。
2 协方差矩阵重构与旁瓣相消
对主瓣干扰的抑制是导致方向图发生畸变的主要原因,因此在一级旁瓣对消器中,需要保证抑制旁瓣干扰的同时保持主瓣内的信号和干扰不发生变化,此时需要对采样协方差矩阵进行修正。
对协方差矩阵进行特征分解得到:
(9)
式中:λi,ui分别为特征值和对应的特征向量,并且将特征值按从大到小排序,即满足λ1≥λ2≥…≥λN;Λs=diag[λ1,λ2,…,λL]为L个大特征值组成的对角阵,对应L个干扰信号的特征值;Us=[u1,u2,…,uL]为其特征向量共同构建的矩阵,张成干扰信号对应的信号子空间;Λn=diag[λL+1,λL+2,…,λN]为N-L个小特征值组成的对角阵,对应噪声信号的特征值;Un=[uL+1,uL+2,…,uN]为其特征向量组成的矩阵,构成噪声子空间。一般信号特征值远大于噪声特征值,由此作为区分标准。
由于自适应波束形状可以表示为在静态方向图上减去特征波束方向图[11],其表达式如下:
(10)
式中:Fq(ξ),Fj(ξ)分别表示静态方向图与第j个特征向量对应的特征方向图。因此,将主瓣干扰对应的特征值降低至噪声平均功率水平来去除主瓣干扰对方向图的影响,其表达式如下:
(11)

(12)
式中:Ums为主瓣子空间[16],可以由主瓣协方差矩阵经特征分解后,大特征值对应的特征向量近似等效[17]。主瓣协方差矩阵由下式得到:
(13)
式中:φ表示主瓣范围。再将其进行特征分解得到
(14)
式中:Λms为由前K个大特征值组成的对角阵;Λns为由剩下的特征值组成的对角阵。由于φ为主瓣范围,因此Ums可以近似表示主瓣子空间。根据式(12)中相干系数的结果,接近1则是主瓣干扰。此时重构后的协方差矩阵为
(15)

再将上述得到的旁瓣干扰与噪声协方差矩阵代替式(5)中的Rx,得到新的旁瓣对消器的和通道自适应权重系数:
(16)
旁瓣对消器的输出即为抑制旁瓣干扰后的信号,此时的方向图在旁瓣处产生零深,抑制了旁瓣干扰,同时主瓣内方向图形状不受到影响。对比文献[5]和文献[6]中的方法,本文抑制旁瓣干扰的过程中不需要对干扰方向进行预估计,减少了计算量。最后在差通道进行同样的处理后可以得到抑制旁瓣干扰的四通道数据。
3 主瓣干扰抑制与单脉冲测角
旁瓣对消器输出为抑制旁瓣干扰后的信号数据,而主瓣干扰则仍然保留,需要对主瓣干扰进行抑制才能分辨目标信号以及对目标信号测角。主瓣干扰抑制方法是利用四通道数据,沿一个方向抑制干扰形成自适应零点,同时保持另一个方向上的单脉冲比不变,即利用方位(俯仰)差通道作为辅助通道,抑制和通道中的方位(俯仰)向的干扰,再利用双差通道作为辅助通道,抑制俯仰(方位)差通道中的方位(俯仰)向的干扰。主瓣干扰对消与测角的处理流程如图2所示。

图2 自适应单脉冲测角流程图
其中,俯仰和通道和俯仰差通道的输出分别为
(17)
式中:yΣ(t),yΔA(t),yΔE(t),yΔΔ(t)分别表示和通道、方位差通道、俯仰差通道及双差通道输出;waE_Σ和waE_Δ为使输出功率最小的自适应权值[9],根据维纳滤波理论,自适应权重为
(18)
式中:PAB表示信号A和信号B的互相关功率;(·)*表示取共轭。此时结合旁瓣干扰对消与主瓣干扰对消后的俯仰向单脉冲鉴角曲面可以表示为
(19)
文献[9]中证明了,假设方位向和俯仰向方向图相互独立,在静态方向图假设下,沿方位向抑制主瓣干扰后,俯仰向的单脉冲比与静态单脉冲比相同;而在抑制旁瓣干扰后,自适应方向图与静态方向图在主瓣范围内可以近似一致。因此,式(19)所得到的俯仰向鉴角曲面在主瓣测角范围内的形状与静态方向图相似,即这种两级处理抑制干扰的方式不会导致测角错误。
类似地可以得到方位和通道和方位差通道的输出如下:
(20)
式中:
(21)
同样方位向上的单脉冲鉴角曲面表示为
(22)
在得到抑制干扰的和通道和差通道数据后,将信号进行脉冲压缩进一步提高信噪比,再根据和通道检测判断目标位置后,根据差比和的比值与静态方向图下的鉴角曲线斜率得到目标在俯仰维和方向维上的角度,实现对目标的精确角度定位。
4 仿真结果
4.1 仿真场景设置
采用由16×16个阵元组成的平面阵进行仿真,两个方向上的阵元间距均为半波长,阵列指向为(0°,0°),目标放置在(0.5°,-0.8°)位置,并假设目标的回波信号为带宽10 MHz、脉宽5 μs的线性调频信号,信噪比为0 dB,空间中还存在3个干扰信号,均为噪声压制干扰,其中主瓣干扰位于(-1.5°,1°),干噪比为25 dB,两个旁瓣干扰分别位于(15°,0°)和(3°,17°),干噪比分别为50 dB和55 dB。信号的采样数为256,并假设采样协方差矩阵中不包含目标信号。
4.2 旁瓣对消器输出结果
图3表示对采样协方差矩阵谱分解后的结果,图3(a)中包含一个主瓣干扰与两个旁瓣干扰的谱峰,而计算重构后的协方差矩阵的空间谱如图3(b)所示,主瓣方向的信号的能量已经处于噪声功率水平,旁瓣干扰信号的能量则有略微的下降。图4表示旁瓣对消器的等效自适应方向图在俯仰角为0°时的剖面图,可见方向图在旁瓣干扰(15°,0°)处形成凹陷,而在主瓣范围内能保持与静态方向图形状一致。

图3 采样信号的空间谱

图4 天线方向图
比较等值加权后的和通道信号与经过旁瓣对消器处理后的和通道信号,图5(a)和图5(b)为未消除旁瓣的接收信号,受干扰的影响,接收信号的功率很大,目标信号完全淹没在干扰信号当中,无法分辨,图5(c)和图5(d)为经过旁瓣对消器后的和通道输出信号,由于抑制了大功率的旁瓣干扰,可以看到输出信号的功率大幅度降低,但输出信号中仍然包含主瓣干扰信号,由于仿真采用线性调频信号的脉冲压缩增益约为17 dB,小于主瓣干扰信号的功率,所以从脉冲压缩后的信号中仍然无法分辨目标信号。
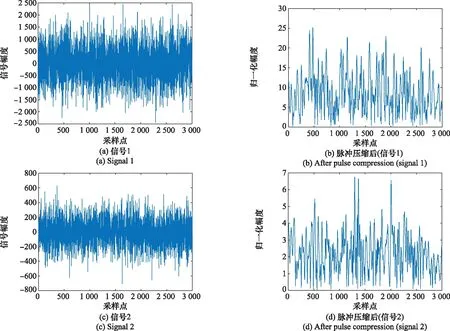
图5 接收信号
4.3 主瓣对消器输出结果和自适应方向图
对旁瓣对消器输出的信号进行重新采样,通过式(17)和式(18)计算抑制主瓣干扰后的俯仰和通道数据如图5(e)和图5(f)所示,可见在抑制主瓣干扰后,信号已经从干扰中浮现出来,并且由于自适应处理后信噪比的提升,可以从未进行脉冲压缩的信号中分辨出目标信号,进行脉冲压缩后,通过查找信号峰值可以提取目标所在位置。
利用式(19)得到抑制方位向干扰后的俯仰和与俯仰差的自适应二维方向图如图6所示,和差天线方向图均在主瓣干扰的方向-1.5°上形成一条沿俯仰向的凹口,并且在两个旁瓣干扰角度上形成了零陷,抑制了干扰。在单脉冲测角范围(-3°,3°)内,沿目标的方位角0.5°处鉴角曲面在俯仰维上的切面如图7所示,可以看到本文方法得到的单脉冲比曲线能保持与静态单脉冲比近似,而直接自适应处理后的单脉冲比曲线发生明显畸变。

图6 俯仰向自适应方向图

图7 目标方位上俯仰向单脉冲比
同样,为了对目标的方位角进行估计,利用式(20)沿俯仰向抑制干扰,保持方位向上的单脉冲比不变。抑制俯仰向干扰后的和差自适应二维方向图如图8所示,在主瓣干扰角度的方向上产生一条凹线,沿目标的俯仰角-0.8°处鉴角曲面在方位维上切面如图9所示,单脉冲比曲线也与静态单脉冲比近似。

图8 方位向自适应方向图

图9 目标方位上方位向单脉冲比
4.4 单脉冲测角结果及测角精度分析
利用脉冲压缩后的信号进行测角,取峰值点作为目标所在点,做30次测角得到结果如图10(a)所示,测量结果分布在目标点周围,证明目标测角偏差不大。在同一个波束范围的不同距离维上放置两个角度分别在(1°,0.1°)位置和在(-0.9°,1.6°)位置的额外目标,对多个目标分别测角,得到测量结果如图10(b)所示,可以看到目标的角度测量结果均在其所在真实角度附近,证明了本方法对不同角度下目标也存在较高的测量精度。
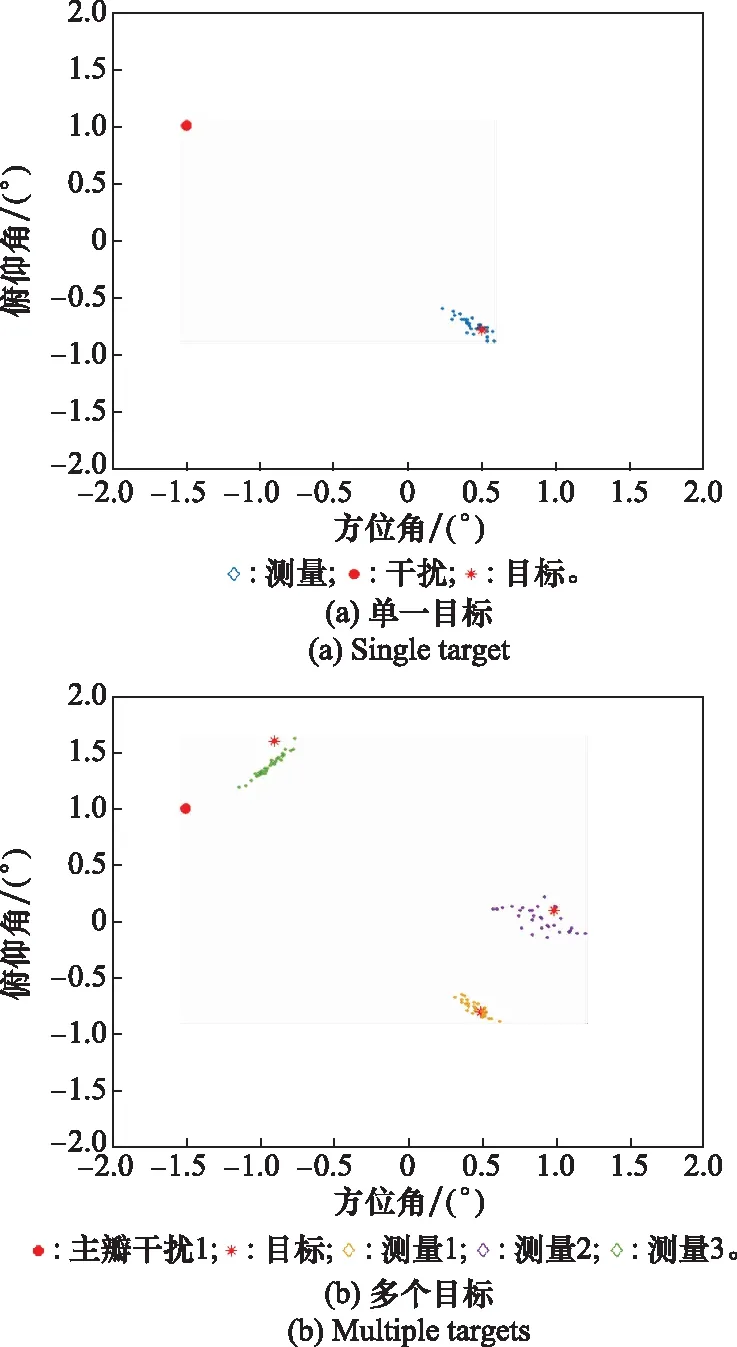
图10 目标角度测量结果
采用均方根误差(root mean square error, RMSE)作为评估测角精度的方法[18],RMCE定义如下:
(23)
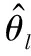
图11表示在仿真的干噪比不变的条件下,经30次仿真得到的测角RMSE随信噪比的关系,可见在低信噪比下测角精度随信噪比增加而提升,当满足一定信噪比后,测角精度趋近理论值,因此实际环境中需要采用脉冲压缩和相参积累等技术提高信噪比来提升测角精度。图12则表示在信噪比维持不变的条件下,信号与主瓣干扰的信干比对测角均方根误差的影响。从仿真结果来看,在干扰强度较强时,主瓣干扰对消器已经对干扰进行了抑制,所以测角精度并不会由干扰的减弱而有明显的变化,而在实际测试中则需要考虑到系统的动态范围,防止对消干扰后的回波信号中不存在目标信号。
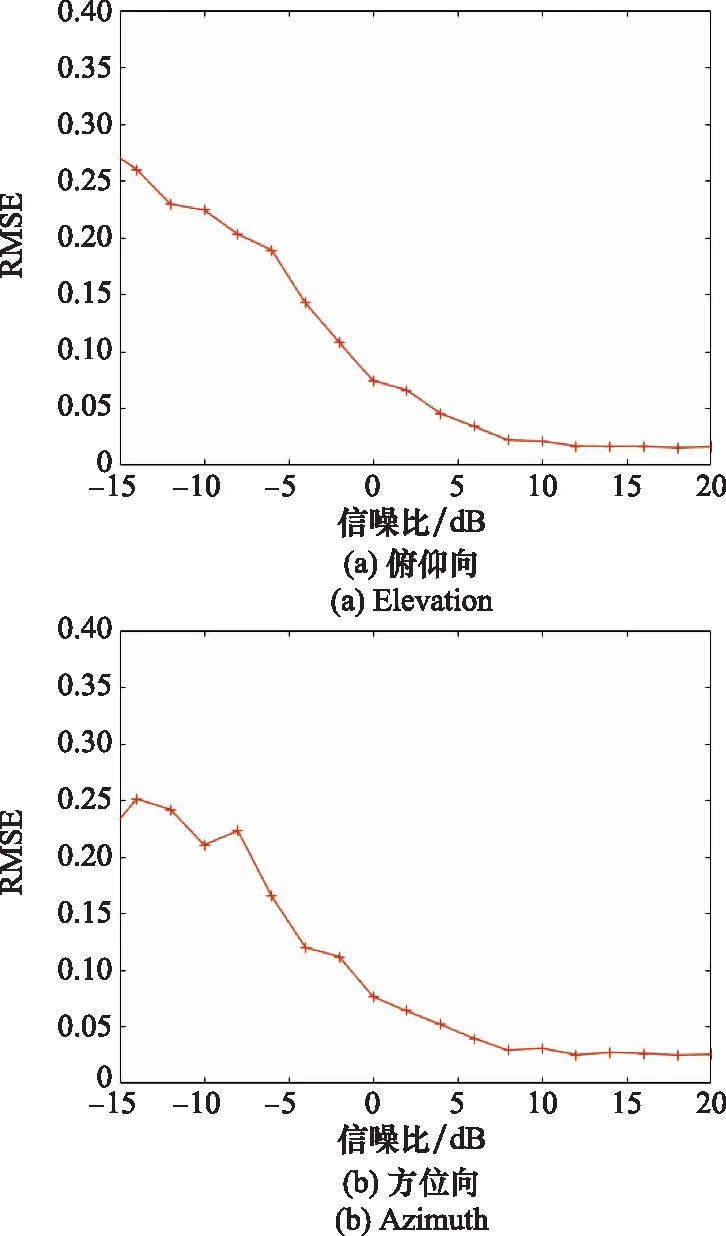
图11 均方根误差随信噪比的关系图

图12 RMSE随信干比的关系图
测试干扰环境不变,仿真目标在测角范围内的各个位置下测角精度的变化。利用下式计算测量角度与真实角度的偏差:
(24)
式中:ks为和差比斜率。
图13表明当目标方位角与主瓣干扰的方位角度接近时,其在俯仰向上的偏差增大,测角精度恶化,而在其他方向上大致相同,即目标主要在干扰角度方向的测角误差较大,这是因为在测量俯仰维角度时,会对干扰方向角度的沿线全部抑制,此时对信号的抑制造成大的测角误差,同样当目标俯仰角与主瓣干扰的俯仰角度接近时,其在方位向上的测角精度也会恶化,当存在这类情况时,应调整阵列角度或采取其他测角方式来避免发生测角错误。

图13 理论测角偏差
5 结 论
本文提出了一种适用于广义旁瓣对消结构的相控阵的自适应单脉冲测角方法,利用旁瓣干扰对消器抑制旁瓣干扰,再利用主瓣干扰对消器在一个方向上抑制干扰,保持另一个方向上的测角精度,并采用了线性调频信号进行仿真验证,结果表明该方法能在同时存在主瓣干扰和旁瓣干扰的条件下实现高精度的测角。此外,本文还分析了目标不同信噪比以及与干扰目标相对位置对测角精度的影响,并给出了保持高精度测角的建议。所提方法不需要消耗高的自由度,也不需要预先估计干扰目标方向,方便工程的实现,具有较高的工程应用价值。
