基于信号传播修正的GNSS干扰源质心定位方法
2021-07-27杨志伟陈奇东廖桂生甄卫民
刘 睿, 杨志伟, 陈奇东,*, 廖桂生, 甄卫民
(1.西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2.中国电波传播研究所, 山东 青岛 266107)
0 引 言
全球卫星导航系统(global navigation satellite system, GNSS)的信号落地功率低,约为-130 dBm。同时,信号采用扩频体制,造成其功率谱密度更低,频谱严重淹没在环境噪声中,容易受到电磁干扰的影响[1]。目前,GNSS系统面临着日益严重的干扰威胁,干扰事件也日益频繁发生。针对GNSS系统的导航对抗已成为现代战争中夺取制胜信息的关键[2],对于干扰源快速有效的定位成为保障国防安全和通信、电力、民航等关键设施GNSS安全应用的重要手段。
常用的GNSS干扰源定位方法有基于波达方向(direction of arrival, DOA)的定位方法[3],基于到达时间差(time difference of arrival, TDOA)的定位方法[4]和基于接收信号强度(received signal strength,RSS)的定位方法[5]。其中,基于DOA的定位方法需要接收机配备阵列天线以获取无线电信号的到达角度;基于TDOA的定位方法要求接收机配备高精度、高稳定度的时钟以维持接收机之间的同步,通常需要GNSS授时,而GNSS在受干扰情况下难以准确授时;因基于RSS的定位方法设备复杂度低而广泛应用于GNSS干扰源定位,但定位方程求解复杂且定位精度较低。文献[6]提出了基于差分到达信号强度(differential RSS, DRSS)的定位方法,一定程度上差分掉接收机之间的测量误差和作为未知量的干扰功率,提升了RSS定位方法的定位精度,但没有解决定位方程求解复杂的问题。文献[7]通过求解被干扰接收机的位置质心实现对目标干扰源的定位,解决了RSS方法迭代收敛困难的问题,但求解质心时没有考虑针对接收机受干扰的情况分配权重,定位精度较低。文献[8]在文献[7]的基础上,根据测量得到的干扰源RSS对权值进行调整,一定程度上提升了定位精度。但上述基于RSS的定位方法均采用理想传播模型,未考虑复杂场景(如城市环境中不开阔、多径等)给定位方法带来的严重困扰。
本文针对上述问题,提出了一种基于载噪比加权和干扰信号传播误差修正的GNSS干扰源质心定位方法。该方法通过测量GNSS接收机的载噪比实现对目标干扰源的定位,实现简单,无需对GNSS接收机做任何软硬件的改动,适用于大数据场景下的GNSS干扰源定位。同时,基于接收机受干扰程度对质心定位方法进行加权,在减少计算复杂度的同时保证定位效果;还采用神经网络方法建立传播模型,准确确定传播影响因子,提升定位精度。最后通过实验对比了本文方法与文献[7-8]的定位方法,结果表明本文定位效果具有明显提升。
1 定位模型
本文GNSS干扰信号定位场景如图1所示,在目标监测区域内随机分布多个GNSS接收机,并且接收机的坐标已知,通过对接收机的坐标[xi,yi]加权求和,确定目标干扰源位置[xt,yt],利用GNSS卫星信号载噪比确定权值,受干扰影响越大的GNSS接收机,其卫星信号载噪比的变化越大,质心定位所占权重应越大。

图1 GNSS干扰信号定位场景
2 所提方法描述
2.1 干扰源的加权质心定位方法
加权质心定位方法在文献[9]中首次被提出,应用于Zigbee设备的定位。在本文应用场景中,GNSS接收机坐标为Ci=[xi,yi],1≤i≤N,目标干扰源位置Ct=[xt,yt]的估算公式如下:
(1)
式中:ωi为接收机i的对应权值,权值的大小取决于对应接收机与干扰源距离的大小。两个接收机i=a,i=b的权值满足以下公式:
(2)
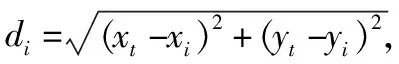
L=Pt-Pr=L0+10αlgd+v
(3)
式中:L为传播路径损耗;Pt为发射功率;Pr接收功率;L0为距离发射机1 m处的传播损耗;d为发射机与接收点的距离;α为路径损耗指数;v是表示噪声的高斯随机变量。对于本文所涉及的应用,接收功率Pr可由GNSS提取的干扰源RSS代替。取接收机i=1为参考接收机,将2≤i≤N与参考接收机的RSS进行差分,利用式(3),可得出差分信号强度的对数表达式:
(4)
式中:RSSi、RSS1分别为接收机i和参考接收机的干扰源RSS,由于接收机分布的空间区域不大,空间噪声值几乎一致,因此v1-vi接近于0,可忽略。将式(4)代入式(2)得出:
(5)
将式(5)代入式(1)即可求出目标干扰源的位置。下文介绍通过引入载噪比实现式(5)中权值的估计方法。
2.2 基于载噪比的干扰权值估计方法
GNSS接收机在跟踪阶段会实时估算卫星信号的载噪比,干扰信号使接收机的载噪比减小,文献[11]给出了干扰影响下,GNSS接收机的载噪比计算方法,公式如下:
(6)
式中:(C/N0)eq为受干扰影响下的等效载噪比,C/N0为无干扰下的载噪比;J/C为干扰功率与卫星信号功率之比;Q为与发射信号和接收信号类型相关的扩频处理抗干扰品质因子;Rc为伪码速率。以dB·Hz为单位,式(6)可表达为
(C/N0)eq,dB≜10lg(C/N0)eq=
(7)
式中:(C/N0)dB=10lg(C/N0),单位为dB·Hz;(J/C)dB=(J)dB-(C)dB=10 lg(J/C),单位为 dB。可以由式(7)导出基于载噪比的干扰RSS对数表达式:
RSS=(J)dB=(C)dB+
(8)
式中:(C)dB=10lgC。式(8)建立了基于GNSS接收机的观测载噪比(C/N0)eq,dB干扰到达信号强度RSS的估算方法。依据式(8)可得出基于观测载噪比(C/N0)eq,dB的DRSSi对数表达式:
(9)
式中:
(10)
由于不同接收机的(C)dB、Q和Rc在本文应用场景中取值相同,所以可在推导过程中可被消去。
将式(9)代入式(5),可得
(11)
将式(11)代入式(1)中,可得出基于GNSS接收机载噪比加权的干扰源质心定位方法的定位结果:
(12)
由式(12)可知,若实现对干扰源的定位需正确设定参数α和β。下文给出这两个参数的确定方法。
2.3 基于神经网络建模的参数α和β的确定方法
通常基于RSS的定位方法采用自由空间传播模型,将参数α取值为2,或者利用传播模型确定传播路径损耗,从而确定参数α。常用的传播模型包括Hata模型[12]、SUI(stanford university interim, SUI)模型[13]、Lee模型[14]和Egli模型[15],上述模型计算方便且限制条件少,但传播路径损耗导致预测精度较低,无法适用于所有传播场景。本文提出了基于神经网络建模参数α的确定方法,利用实测数据并采用神经网络方法构建应用区域内参数α的模型,可显著提升定位效果。
人工神经网络方法在信息处理中模拟生物神经系统的行为,可为一组特定的输入输出找到最佳的函数拟合,并对未知的数据集进行插值和外推[16]。人工神经网络由神经元组成,神经元模型如图2所示。设向量x=[x1,x2,…,xq]T为神经元输入,对神经元进行加权求和并添加神经网络偏置b,可得u=ωTx+b=ω1x1+ω2x2+…+ωqxq+b,其中ω=[ω1,ω2,…,ωq]T为权值。将u通过激励函数f(·)得到输出结果y=f(u),其中激励函数可为任何非线性可微函数。用目标数据t减去激励函数输出值y可得神经元输出误差e,即e=t-y。神经元模型采用某种优化准则,输出最小误差e。在本文应用场景下,目标值t为实测得到的参数α,y为网络输出的参数α。

图2 神经元模型
本文神经网络的设计依据为对下文实测数据的预测效果统计,采取最优预测效果的隐层神经元个数、激活函数和学习方法,具体统计结果见第3节。文献[17]表明单隐层神经网络可以逼近任何复杂的非线性函数,文献[18-19]表明单隐层针对回归问题具有良好的预测精度和泛化能力。隐藏层数越多不仅会增加方法复杂性,当训练数据量不够大时,还会导致模型更易拟合过度。本文神经网络输入变量个数为4个,分别为干扰源经度、干扰源纬度、接收机经度和接收机纬度;输出变量为待确定参数α;隐层神经元个数为8个;神经元激活函数采用tansig函数;学习方法采用列文伯格-马夸尔特(Levenberg-Marquardt, LM)算法[20]。对应神经网络方法架构如图3所示。
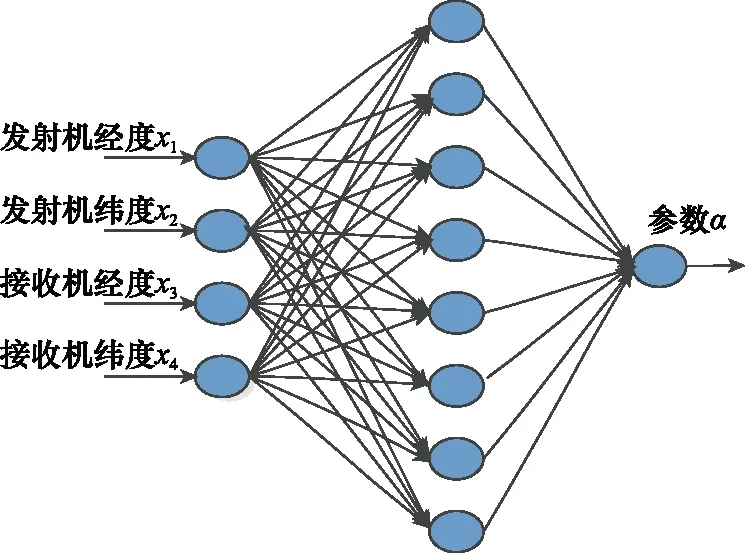
图3 本文神经网络设计架构
在确定神经网络模型参数α后,利用实测数据对已知干扰源进行定位,遍历所有参数β可能取值,对不同取值的定位效果进行统计,采用最优定位效果对应的参数β作为最终取值。
2.4 基于GNSS接收机载噪比加权和干扰信号传播误差修正的干扰源质心定位方法流程
基于GNSS接收机载噪比加权和干扰信号传播误差修正的干扰源质心定位方法流程如图4所示。首先利用确定好的参数β,依据式(12)对干扰源进行首次定位,各接收机的参数α均取默认值2;然后利用构建好的神经网络模型参数α对首次定位结果进行迭代修正,最终收敛得到更准确的干扰源位置。
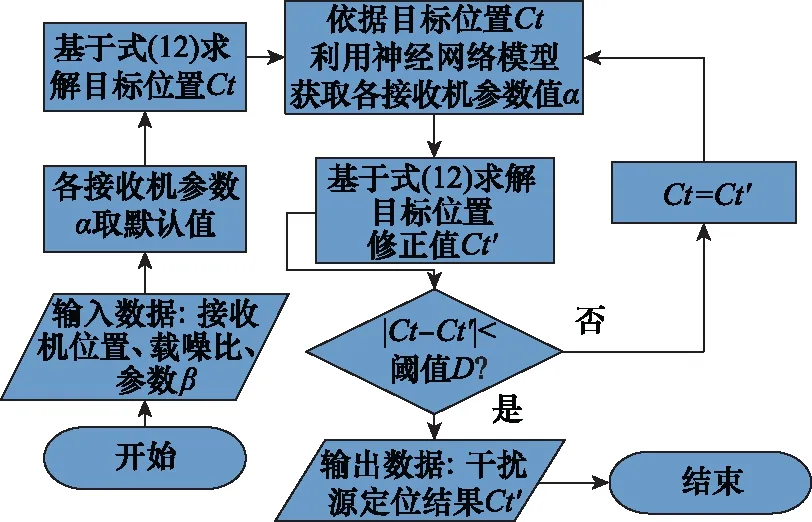
图4 基于信号传播修正的GNSS干扰源质心定位方法流程图
3 实验分析
3.1 数据采集
实验设备如图5所示,包括GNSS接收机36台、GPS L1干扰机1台、多系统多频点导航接收机1台和笔记本电脑1台。GNSS接收机采用常见手机,用于数据采集,手机具备GPS L1定位功能,手机安装载噪比记录APP,将包含载噪比和定位信息的NMEA数据以文件形式存储于手机中。采用车载功率可调的GPS L1干扰机作为发射源,干扰机最大输出功率为10 W。该车同时搭载多系统多频点导航接收机,可在GPS L1频点被干扰时获得干扰源准确位置。采集数据以文件形式汇入到笔记本电脑,并由该电脑进行干扰定位处理和实验数据分析。

图5 实验设备
实验测试选用地面有建筑物和植被的场景,该场景下信号传播存在遮挡、反射等,可产生衰落、多径等效应,场景如图6所示。其中,A区、B区、C区、D区、I区为低矮密集植被覆盖区,E区为工厂厂房,F区为居民楼房,J区、K 区为高大稀疏植被覆盖区,G区、H区、L区为农田,其中L区有一处水塘。

图6 实验场景
在该场景中,接收机布局及数据测试路线如图7所示。图7中,黑色方形点为接收机位置,接收机随机分散布,设于约为2 km×2 km的区域内。在无干扰情况下,记录接收机准确位置坐标,每秒采样获取其载噪比数据并记录该数据采集时间。车载干扰机行驶路线为图7中所标记的9条路线。车载干扰机在每条路线上匀速缓慢行驶5 min,36台GNSS接收机获取数据总量为97 200条,并将整个数据集被随机分为70%的训练集和30%的测试集。
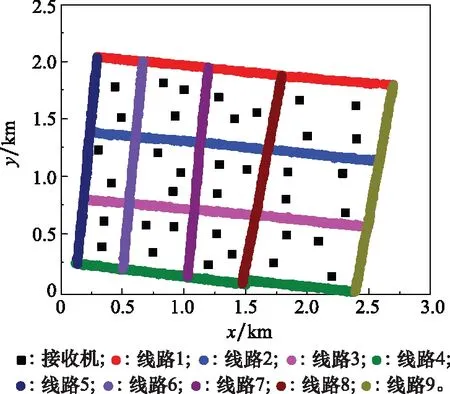
图7 接收机布局及数据测试路径
3.2 基于神经网络建模的参数α和β的确定
利用上文训练集采用神经网络方法构建参数α模型,模型采用单隐层四输入设计,本节内容给出隐层神经元个数、激活函数和学习方法对建模效果的影响,从而确定最合适的神经元数目、学习算法和激活函数。建模效果采用决定系数(R-square,R2)进行评价,R2计算公式如下:
(13)

(14)
神经网络设计的神经元个数应在保证模型预测精度的同时,尽量取值较小以避免过度拟合。本文建模过程中遍历统计神经元个数从1到16的建模效果,图8给出了不同隐藏神经元数量对应的R2值。该实验学习方法为LM算法,隐藏层和输出层激活函数均为tansig。图8结果表明神经元个数为8时,R2为最大值0.983 1,建模效果最好。

图8 不同神经元个数对应的R2取值
神经网络设计需同时考虑隐层和输出层激活函数的选择,本文对目前常用的3种激活函数进行不同隐层和输出层的组合,对生成模型的参数R2进行统计,表1给出了统计结果。3种激活函数分别为logsig函数、tansig函数和purelin函数,对应函数公式如下:
fpurelin(u)=u
(15)
(16)
(17)
该实验神经元个数为8,学习方法为LM算法。表1结果表明隐层和输出层的激活函数均采用tansig函数时对应R2为最大值0.983 1,建模效果最好。

表1 不同激活函数组合对应的R2取值
神经网络学习算法主要是构建合适的损失函数,损失函数的构建需要考虑模型在训练数据集上拟合程度的同时,还要防止出现过拟合现象。本文算法通过对损失函数取值最小化实现神经网络模型的权重ω和偏置b的确定。目前常用的学习算法为LM算法、BFGS(Broyden Fletcher Goldfarb Shanno, BFGS)拟牛顿算法[21]、量化共轭梯度(scaled conjugate gradient,SCG)法[22]、弹性传播(resilient propagation training,RP)算法[23]、Fletcher-Reeves共轭梯度(conjugate gradient backpropagation with Fletcher-Reeves updates, CGF)法[20]和Polak-Ribiére共轭梯度(conjugate gradient backpropagation with Polak-Ribiére updates, CGP)法[24]。本文对上述6种方法生成模型的R2参数进行统计,表2给出了统计结果。该实验神经元个数为8,隐藏层和输出层激活函数均为tansig。表2结果表明采用LM算法进行学习时,R2为最大值0.983 1,建模效果最好。上述仿真结果表明,针对本文应用,隐层神经元个数需设计为8个,隐层和输出层神经元激活函数应均采用tansig函数,学习方法需采用LM学习算法。采用本节神经网络设计构建的实验区域的参数α模型如图9所示。图10给出采用参数α模型的36台接收机采用配备不同参数β对应的定位均方根误差(root mean square error, RMSE),可以看出随参数β增加,定位RMSE降低,当参数β≥3时,定位RMSE趋于稳定,因此本文实验参数β取值为3。

表2 不同学习算法对应的R2取值

图9 实验区域的参数α模型

图10 采用参数α模型的36台接收机采用不同参数β对应的定位RMSE
3.3 定位结果
在完成参数α神经网络模型构建的基础上,给出本文方法的定位结果。图11~图13分别给出了不同接收机数量下,文献[7]、文献[8]和本文所提方法定位结果的对比。

图11 12台接收机定位结果

图12 24台接收机定位结果

图13 36台接收机定位结果
对上述场景定位结果的RMSE进行统计,如表3所示,实验结果表明,参与定位的接收机数量越多,定位精度越高,同时相对于文献[7]、文献[8]方法,本文方法定位精度有显著提升。

表3 定位RMSE
4 结 论
本文提出了一种基于载噪比加权和干扰信号传播误差修正的GNSS干扰源质心定位方法,利用通用GNSS接收机现有的载噪比信息就可实现GNSS干扰源的准确定位,无需改变接收机现有软件与硬件。创新性地采用神经网络方法,准确预测复杂环境的传播影响因子,基于参数α模型和加权质心定位方法提升了复杂场景下传统基于RSS定位方法的定位精度。实验表明,本文所提方法的定位精度得到明显提升。
