基于改进Johnson-Cook模型的5083P-0铝合金动态本构关系研究
2021-07-27李恒奎张光瀚赵晓春肖守讷朱志武
李恒奎 张光瀚 赵晓春 肖守讷 朱志武
(1 中车青岛四方机车车辆股份有限公司,青岛 266111)
(2 西南交通大学牵引动力国家重点实验室,成都 610031)
(3 中国铁路济南局集团有限公司青岛机车车辆监造项目部,青岛 266111)
文 摘 为研究5083P-0 铝合金在高应变率下的力学行为及本构模型,通过RPL100 材料试验机和分离式霍普金森压杆(SHPB),对5083P-0 铝合金进行了准静态及应变率范围950~3 000 s-1的冲击动态压缩实验。结果显示随着应变率的增加,5083P-0 铝合金的屈服强度、流动应力增加,应变硬化率减小,具有应变硬化效应,正应变率效应以及热软化效应。对其塑性变形原理进行分析发现,滑移系的作用导致材料发生较大的塑性变形,同时由于绝热温升的产生,材料表现出应变硬化与热软化机制相竞争的情况。在Johnson-Cook 模型的基础上对应变率项进行改进,并引入绝热温升,改进的Johnson-Cook 模型能够能较好地描述该材料的应变率效应并能准确地描述其流动应力。最后采用新的应变率进行补充实验,通过对比验证了模型的合理性。
0 引言
铝合金材料因其具有低密度,高强度和高塑性等优良性能而广泛应用于日常生活、工业生产以及高速列车车体结构中[1-4]。在对铝合金的使用过程中,不可避免地可能会受到冲击动态载荷的作用,如车辆碰撞、列车零部件间的撞击等[5]。经验表明,冲击动态载荷条件下与准静态载荷条件下材料的力学性能会有所不同。铝合金材料会出现随着应变率的增大,屈服应力与流动应力提高、应变硬化率降低等现象。因此,对于铝合金在冲击动态载荷下的力学性能亟待研究。
随着冲击动态力学发展以及实验设备的革新,国内外学者也更加系统地研究了各牌号铝合金材料的冲击动态力学性能。诸多研究表明,铝合金材料的力学性能会随着不同的合金成分、含量以及加工硬化、热处理的不同,而产生不同的力学性能。然而,关于研究5083P-0 铝合金力学性能的文章甚少,特别是其冲击动态力学性能的研究。
近年来,由于高铁迅速发展,铝合金材料的冲击动态力学性能逐步得到国内外研究者的广泛重视,并获得了较多的成果。目前对于铝合金动态力学性能的研究往往集中在实验部分上,通常情况下铝合金材料具有较弱的应变率敏感性,但一些研究表明铝或者铝合金在某些条件下应变率敏感性会增强。对于大部分铝合金,如7150[6]、3004[7]、6061[8]铝合金都具有明显的应变率强化效应,即当温度一定时,屈服应力和流动应力随着应变率的增大而明显增大。还有研究表明不同牌号的铝合金材料应变率敏感性会有所不同,如7050,2024等铝合金表现为应变率不敏感[9-10];而3004、2219等铝合金表现出应变率敏感性[11-12]。
国外对5083 铝合金进行了较早的研究[13-14],国内已对5083 铝合金的超塑性[15]、高温本构[16]和中低应变率[17]的力学性能进行了研究。对于5083的本构研究方面,高宁[18]、晏宁[19]等对5083 铝合金进行了宽应变率下的实验,通过Johnson-Cook(J-C)模型和Zerilli-Armstrong(Z-A)模型合理描述了5083 铝合金的拉伸“V”型率效应特征,并引入损伤变量将J-C 模型改进,使模型得以描述5083的软化效应。
5083P-0 铝合金的准静态力学性能可以从材料手册中获得,但其冲击动态力学性能很难获得。鉴于此,本文通过冲击动态压缩实验获取5083P-0 铝合金应力应变曲线,进而揭示该材料在不同应变率加载条件下的冲击动态力学性能。
1 实验及原理
5083P-0 铝合金动态压缩实验利用分离式霍普金森压杆完成,采用圆柱形试样,尺寸为Φ6 mm×4 mm。实验原理如图1所示。
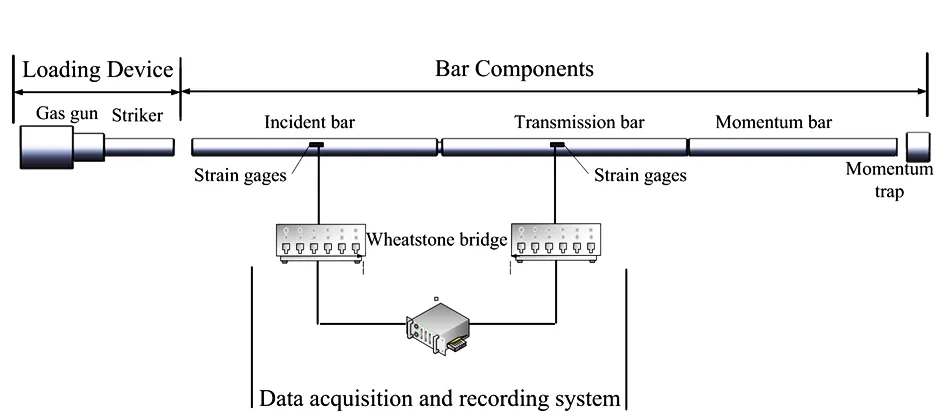
图1 SHPB设备示意图Fig.1 Schematic diagram of SHPB equipment
分离式霍普金森压杆由入射杆、透射杆和吸收杆组成,其中压缩实验设备的入射杆直径14.5 mm、长度400 mm,透射杆直径14.5 mm、长度为525 mm,最大撞击速度为60 m/s。此外,还包括超动态应变仪、高速摄像头以及外部数据采集系统。实验后将得到的波形采用二波法处理[20]。实验时,首先调整汽缸的气压,子弹受气缸内的压力进而发出,通过控制气压来控制子弹的速度,进而控制了加载应变率,加载气压与子弹射出速度的关系曲线如图2所示。

图2 气压压强与子弹速度关系图Fig.2 Relationship between air pressure and bullet velocity
由一维应力波理论并引入均匀性假设[21],得到材料的应变率(t)、应变ε(t)和应力σ(t):
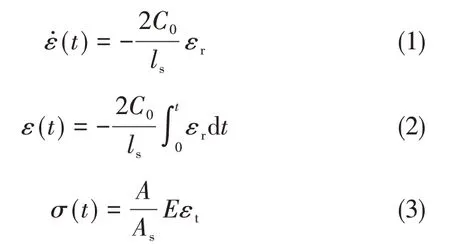
式中,ls、As分别为试样的长度和横截面积,A、E分别为压杆的横截面积、弹性模量,ρ为压杆的密度,εi为入射应变波、εr为反射应变波、εt为输出杆上的透射应变波,C0为应力波在杆中的传播速度。
由此得到试样的应力、应变、应变率与时间的关系,进而得到应力、应变、应变率三者之间的相互关系。
2 实验过程及结果
冲击动态压缩实验加载应变率分别为:950、1 500、2 000、3 000 s-1,在每个加载应变率下进行两次重复实验,若一致性不好,再进行第三次实验。压缩应力应变曲线及塑性段应力应变曲线如图3、图4所示。

图3 冲击压缩加载下的应力应变曲线Fig.3 Stress strain curves under impact compression loading

图4 冲击压缩加载下塑性段的应力应变曲线Fig.4 Stress strain curves of plastic section under impact compression loading
由图3、图4可以看出,在冲击动态下5083P-0铝合金不同应变率的应力应变曲线在弹性阶段基本重合,而屈服应力随着应变率的增加有一个明显的提升,而在塑性阶段,随着应变率的升高流动应力明显升高。说明在高应变率下5083P-0 铝合金表现出明显的应变率效应。与此同时,随着应变不断增加应力也在不断增加,该材料在动态压缩加载下表现出明显的应变硬化效应,塑性变形所示的屈服强度的应变速率依赖性可以通过热激活位错理论来解释。曲线后半段出现应变软化现象,是由于高速冲击会使材料内部产生绝热温升,导致材料出现应变软化现象,该段曲线表现出应变硬化与热软化机制相竞争的情况。
为了更好地说明5083P-0铝合金的力学性能,根据GB/T7314—2005要求[22],准静态压缩实验采用圆柱形试样,尺寸为Φ6 mm×4 mm。采用RPL100材料试验机完成5083P-0铝合金的准静态压缩实验,加载应变率为0.01 s-1。将准静态曲线与动态曲线进行对比,如图5所示。
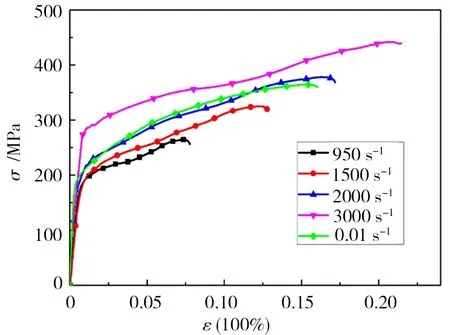
图5 5083P-0铝合金准静态与动态实验曲线对比Fig.5 Comparison of quasi-static and dynamic experimental curves of 5083P-0 aluminum alloy
可以看出在应变率低于2 000 s-1时,材料的动态屈服强度明显低于材料静屈服强度。根据晏宁、高宁的研究[11-12]可知,对于5083铝合金当应变率小于10 s-1时,材料表现出负应变率效应,屈服应力随应变率变大而变小;当应变率大于10 s-1时,材料表现为正应变率效应,屈服应力随应变率变大而变大。因此当材料处于低应变率时的屈服强度反而高于950 s-1、1 500 s-1应变率下的屈服强度。说明无论是准静态还是动态压缩下5083P-0铝合金都有很大的塑性变形。对于大部分金属而言,发生塑性变形主要由孪生和滑移共同作用,由于铝合金为面心立方晶体,其发生孪生时所需的临界分解剪切应力比滑移大,一般情况可以忽略孪生对其塑性变形的影响。因此5083P-0铝合金塑性变形机理主要是晶粒的滑移,在冲击荷载作用下,试样内部晶粒发生滑移、变形。随着参加滑移的晶粒越来越多,起作用的滑移系也越来越多,最终扩散到试样内部的全部滑移系,试样发生较大的塑性变形。
3 Johnson-Cook本构模型
就冲击动力学而言,模拟材料力学响应的本构方程是否标准将严重影响到分析结果的准确性。Zerilli-Armstrong(Z-A)和Johnson-Cook(J-C)模型的推导都是基于经验和半经验模型,它们所涉及的材料常数比物理模型更少,并且只需要有限的材料试验数据,因此可以更有效地用来预测材料的力学性能。目前Johnson-Cook模型是经验模型中使用最广泛的模型之一[23-30],其包括5个材料常数,其中应变率硬化项和温度软化项是最为重要的部分。为了提高Johnson-Cook模型的准确性,本文对模型进行了一些修改,结合Johnson-Cook应变率强化项和温度项改进,为高强度合金材料的流动应力提供精确的估计。
Johnson-Cook模型应力应变关系可表示为[31]:

式中,(A+Bεnp)、(1+Cln)、(1-T*m)分别为描述材料加工硬化效应、应变率效应和温度软化效应。其中σ为Von-Mises流动应力。A为参考应变率和参考温度下的屈服强度,B、n分别为材料硬化模量和硬化指数,C为材料应变率敏感(强化)系数,m为材料温度软化指数,各参数均由实验获得。εp为等效塑性应变,为无量纲等效塑性应变率,为参考应变率。为无量纲化的温度项,Tm、Tr分别为材料的熔点温度(730 ℃)和室温(20 ℃),A在此参考温度下测定。
根据前文中的实验数据来拟合Johnson-Cook 本构方程的各参数。
3.1 确定参数A、B和n
式(4)右边第一个括号项表示T=Tr及=时的σ-ε关系。参数A为材料在参考应变率下的屈服强度,通常将准静态实验的应变率定为参考应变率,即A为准静态实验条件下的屈服强度。但是由于5083P-0存在负应变率效应,若取准静态实验的屈服强度作为参数A的值,会导致动态屈服强度低于准静态屈服强度的曲线无法拟合。根据晏宁的研究[12]5083铝合金在低应变率到中应变率过程中存在负应变率效应,材料的屈服强度逐渐降低,在应变率为10 s-1时到达最小,为149 MPa。而在中应变率到高应变率的过程中,存在正应变率效应,材料的动态屈服强度逐渐提高。因此在试样的初始温度条件下,即T=20 ℃时,选取应变率=10 s-1为参考应变率,根据参考应变率下实验测量所得σ-ε曲线即可确定A、B和n。此时,式(4)可化简为:

首先可以确定A,即材料参考应变率下的屈服应力为149 MPa。
其次确定B和n,将式(5)两边同时取对数,并带入A可以得到关系式:

做出ln(σ-A)-lnε曲线,曲线的截距为lnB,斜率为n(tanα),于是可以得到B和n的值。
3.2 参数C的确定
从J-C模型中可以看出当塑性应变零,且实验处于室温条件下时,此时的应力为动态屈服应力,J-C模型变成:

常温下5083P-0 铝合金的屈服应力与应变率的关系做出了σy-ln图,如图6所示,根据求解n的过程,利用式(7)便可拟合出参数C。

图6 Johnson-Cook本构模型参数C的拟合Fig.6 Fitting parameter C of Johnson-Cook constitutive model
通过准静态常温高温实验,冲击动态实验,得到参数如表1所示。

表1 J-C本构方程参数Tab.1 Parameters of J-C constitutive equation
将两组参数值代入式(4)中,得到5083P-0 铝合金的Johnson-Cook本构方程为:

3.3 改进的Johnson-Cook本构模型
由图6不难发现,σy与ln之间并不是完全的线性关系,高应变率下强化效应更加显著,单纯用线性变化关系来描述并不合适,因此对模型中的应变率强化项作适当修正。假设两者存在指数对应关系,如公式(9)所示,对J-C模型进行改进,并对实验点进行拟合,见图7。
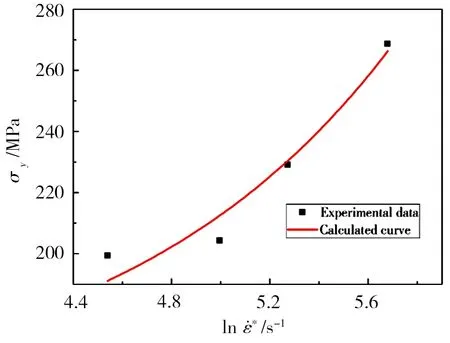
图7 σy与ln ε*拟合关系Fig.7 The fitting relationship between σy and ln ε*
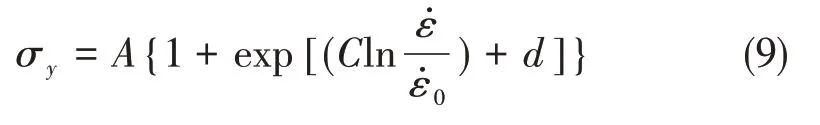
可以看出,该指数能更好的描述σy与ln的关系,因此将J-C 模型的应变率项进行改进,得到改进后的J-C模型:

模型中各参数值见表2。

表2 改进后J-C模型各参数值Tab.2 Parameters of improved J-C model
由式(10)可以看出模型并没有考虑高应变下材料绝热温升的因素。在高速冲击条件下,由于变形速度过快,能量迅速增加,由此产生的热量无法在短时间内向外界传递,此过程可视为绝热条件。而该温度为材料内部温度,温度的测量是实验的难点所在。根据文献[33-34]对于高应变率下材料绝热温升的研究,如果材料变形是在等温环境有热交换的情况下进行的,则流动应力将高于没有绝热的情况。通过间接方法,可以确定变形过程中材料内部温升,即在实验后用量热法测量储存的能量:

式中,ΔW为所做的功,ΔQ为产生的热量,η为塑性功热转换系数,σe为真实应力,ε为真实应变,Cu为室温比热,ρ为材料密度,ΔT为绝热温升。
将5083P-0 铝合金的密度2.70 g/cm3、室温比0.9(J/kg·℃)、塑性功热转换系数0.9 代入式(13)并结合实验曲线计算可得到各加载应变率下的绝热温升,如表3所示。各加载应变率下实验与理论对比图见图8。

表3 各加载应变率对应的绝热温升Tab.3 Adiabatic temperature rise corresponding to each loading strain rate
将J-C在考虑绝热温升后再次改进:

分析图8中四种加载应变率的对比结果可以得出:改进J-C模型的理论与实验曲线拟合良好,反映了应变率效应和绝热温升软化效应对5083P-0铝合金动态压缩过程中流动应力影响趋势,改进J-C模型可较好地描述5083P-0铝合金的动态压缩力学性能。具体表现为:改进J-C模型能更准确地描述各应变率条件下的材料屈服点以及各应变率下的应变率强化效应,同时该模型可以表述材料热软化效应,很好地反映高应变率下应变硬化与热软化机制相竞争的情况。
4 模型的合理性验证
为了验证模型的合理性与应用性,进行一次补充实验,采取与前文不同的应变率进行实验。得到塑性段的应力应变图,如图9所示。

图9 1 300 s-1应变率下的5083P-0压缩应力-应变曲线Fig.9 5083P-0 compressive stress-strain curve at 1 300 s-1 strain rate
将1 300 s-1的应变率代入到式(14),得到1 300 s-1应变率下的5083P-0 的本构方程理论曲线,将实验与理论曲线进行对比,如图10所示。

图10 1 300 s-1应变率下的压缩实验曲线与理论曲线对比图Fig.10 Comparison of compression experimental curve and theoretical curve at 1 300 s-1 strain rate
从图10看到,在新的应变率下该模型也能对实验曲线进行很好的拟合与描述,说明改进后的J-C模型可以对不同工况下的5083P-0 铝合金进行预测与描述,验证了模型的合理性与应用性。
5 结论
对5083P-0 铝合金进行了冲击动态加载实验,得到其不同应变率下的应力-应变曲线。通过对J-C模型改进,得到了更加适用于5083P-0 铝合金的冲击动态本构模型。相关的研究结论如下:
(1)通过5083P-0 铝合金在准静态和冲击动态加载下的压缩实验可以看出,流动应力随着应变的增加而明显增加,5083P-0铝合金具有明显的应变硬化现象;在冲击压缩实验中随着应变率的增加,5083P-0铝合金的屈服应力及流动应力逐渐增加,说明冲击压缩时具有应变率效应;
(2)5083P-0铝合金冲击动态加载下曲线后半段出现应变软化现象,是由于高速冲击会使材料内部产生绝热温升,导致材料出现应变软化现象,该段曲线表现出应变硬化与热软化机制相竞争的情况;
(3)通过对材料屈服应力与应变率的研究,改进J-C 模型中的应变率项,并引入绝热温升对温度项进行改进,使得该模型可以在冲击加载条件下对各应变率范围都能进行很好的拟合。最后添加新的应变率进行补充实验和合理性验证,通过理论和实验曲线的对比,验证了模型的合理性。
