基于有限元模型的三维随机纤维材料微结构设计

2021-07-27李大涛郁汶山蒋劲松

宇航材料工艺 2021年3期

李大涛郁汶山蒋劲松

（1 长安大学道路施工技术与装备教育部重点实验室，西安 710064）

（2 西安交通大学机械结构强度与振动国家重点实验室，西安 710049）

（3 成都飞机设计研究所，强度设计部，成都 610041）

文摘为研究三维随机纤维材料服役环境下的力学性能，提高热防护系统安全服役性能和结构寿命。利用有限元建模软件，建立三维随机纤维材料微结构模型，研究其面内和厚度两个方向的三维随机纤维材料宏观力学性能与几何参数（纤维方向、纤维长度和纤维直径）的关系，获得了三维随机纤维材料厚度和面内宏观力学性能演化规律。结果表明：三维随机纤维材料内部偏移纤维比重越大，厚度方向压缩强度就越高，面内方向压缩强度就越低；压缩强度随纤维长度增加呈上升趋势，在0.9 mm 左右时达到临界值；压缩强度随纤维直径增加呈下降趋势。该研究结果可为三维随机纤维材料制备提供理论基础。

0 引言

高超声速飞行器是世界各国研究和发展的热点［1］，而高超声速飞行器的安全服役需要由高性能的热防护系统（TPS）提供保障，来确保飞行器的关键结构在大气层中高速飞行时免遭烧毁［2］。其中，刚性隔热瓦热防护系统具有质量轻、耐温高等优点，被大面积应用于航天飞机等飞行器中。典型的刚性隔热瓦热防护系统，由刚性隔热瓦、应变隔离垫、室温固化硅胶和外部涂层等组成［3-4］。作为刚性隔热瓦热防护系统中最重要的组成部件——刚性隔热瓦，是一种由无机纤维材料烧结而成的网状结构三维随机纤维材料，且具有孔隙率高、质量轻、隔热性能优良等特点［5-10］。在航天航空领域，刚性隔热瓦除了提供优异的隔热功能外，还必须要具备一定的力学性能。历史上较为经典的案例便是美国哥伦比亚号航天飞机发生的灾难事故［11-13］，让学界和工业界愈加重视构成刚性隔热瓦的三维随机纤维材料力学性能研究，不断改善和提高三维随机纤维材料的力学性能及服役可靠性。

三维随机纤维材料作为刚性隔热瓦热防护系统中最重要构成材料，对高超声速飞行器的安全飞行起到举足轻重的作用。提高三维随机纤维材料性能及使用寿命的关键在于对材料力学性能与细观破坏机制的深入研究。国内LIU 等［7］利用ANSYS 软件分析了三维随机纤维材料的压缩过程，研究发现：在考虑纤维节点弯曲和纤维接触的情况下，模拟结果与试验压缩结果相吻合。LUO 等［14］提出了等效刚度法来模拟纤维之间的接触，并基于模型在承载方向损伤的单元与位置，获得刚性隔热瓦失效的变化过程及程度。LI 等［15-17］建立了考虑残余应力、纤维接触、温度、三维随机纤维材料细观形貌特点的有限元模型，研究了三维随机纤维材料的拉伸、压缩和断裂韧性性能，模拟与试验的结果在较低温度范围内吻合很好。此外，三维随机纤维材料制备过程中，B4C 粉末的用量影响材料孔隙率，石英纤维与莫来石纤维所占质量比等决定材料弯曲强度［2］。为改善三维随机纤维材料的力学性能，一些研究［18-19］从三维随机纤维材料的烧结温度和制备工艺入手，借助简化理论分析模型，提升三维随机纤维材料的压缩性能。

为研究三维随机纤维材料力学性能及使用寿命，本文利用有限元建模软件，建立考虑三维随机纤维材料细观形貌特点的有限元模型，获得三维随机纤维材料厚度和面内方向宏观力学性能随纤维分布角度、纤维直径和纤维长度变化等几何参数变化规律，拟揭示三维随机纤维材料厚度和面内宏观力学性能变化规律，指导三维随机纤维材料的制备。

1 三维随机纤维材料

三维随机纤维材料主要由高纯度的石英纤维和莫来石纤维烧结而成，石英纤维和莫来石纤维都是高性能的无机纤维，耐高温，广泛地应用于隔热材料［2］。例如，美国发展的LI 系列纯石英纤维刚性隔热瓦（三维随机纤维材料），已经成功应用于航天飞机等飞行器中。已有研究表明［6，20］，三维随机纤维材料的制备过程包括：将长纤维切成短切纤维，并将短切纤维与烧结剂（B4C 粉末和可溶性淀粉等）混合起来制桨，将制好的浆倒入模具中并在真空中蒸发掉水分。充分的干燥后，将形成的块状纤维体放入温度为1 473 K 的高温炉内烧结约2 h；烧结过程中，材料内部随机分布的纤维将被烧结到一起。最后，在模具中形成一个孔隙高、内部纤维随机分布的三维网状结构。图1（a）和（b）分别给出了三维随机纤维材料厚度（TTT）和面内（IP）两方向截面的扫描电镜图。从图中可以看出，TTT 方向的截面内，纤维随机分布且具有较高孔隙率，并可以看到镂空结构；而IP方向的截面内，纤维表现出更好的方向性，纤维间隙较小并且堆积到一起。根据IP 方向的堆积结构特点，可以推测此堆积方向基本上为材料的厚度方向，且在烧结过程中，纤维受重力作用，类似一层层地堆积到一起。从而形成IP 方向所示纤维排布规律，而在TTT 方向的截面内由于高温烧结时水分的蒸发与烧结剂的烧蚀而形成镂空结构［21］。

图1 三维随机纤维材料试样截面扫面电镜图Fig.1 The scanning electron microscope images of the 3D RF material in the TTT and IP directions

2 微结构设计方法

2.1 代表性体积单元

代表性体积单元（RVE）在预测材料有效力学性能方面扮演很重要的角色［22］。为了准确、清晰地评估这类三维随机纤维材料的力学性能，需要建立一个可以表征此类材料细观形貌特点的代表性体积单元。在有限元软件ANSYS 中利用APDL 语言编写模拟程序，并利用Beam188 单元来模拟石英纤维［16］。由于设定代表性体积单元中所有纤维为各向同性材料，所以纤维的本构方程中只含弹性模量和泊松比两个参数。室温下石英纤维的断裂强度和弹性模量分别为3.6 和78 GPa［15，23］，泊松比为0.17［7］。另外，纤维为脆性材料，利用最大应力准则判定纤维断裂［6］。

假设代表性体积单元中任意一根纤维在空间分布方向可以通过图2中α和β两个角度确定，并且单根纤维的两个端点分别为K0（x0，y0，z0）和K1（x1，y1，z1）［15］。

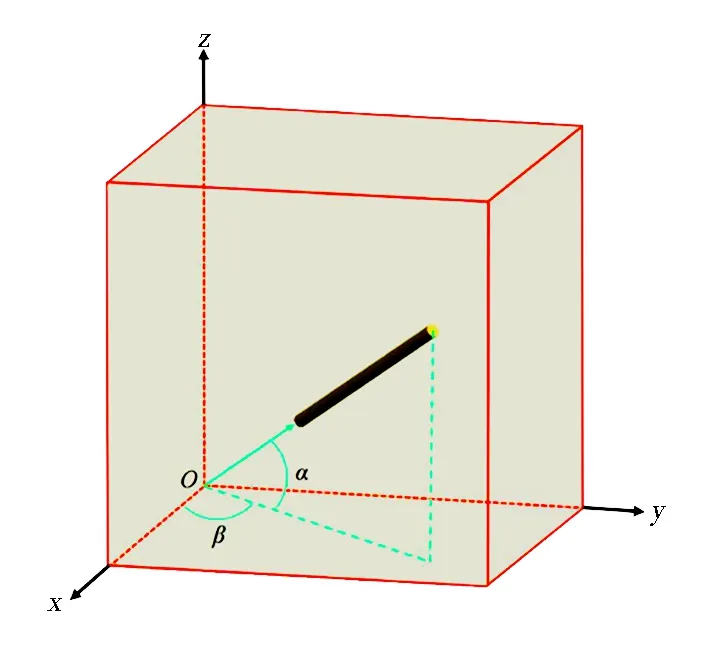
图2 单根纤维在RVE中的空间位置Fig.2 Position of a fiber in representative volume element（RVE）

代表性体积单元模型的大小确定为Lx×Ly×Lz，空间单根纤维的端点K0（x0，y0，z0）和K1（x1，y1，z1）坐标可以表示成［15］：

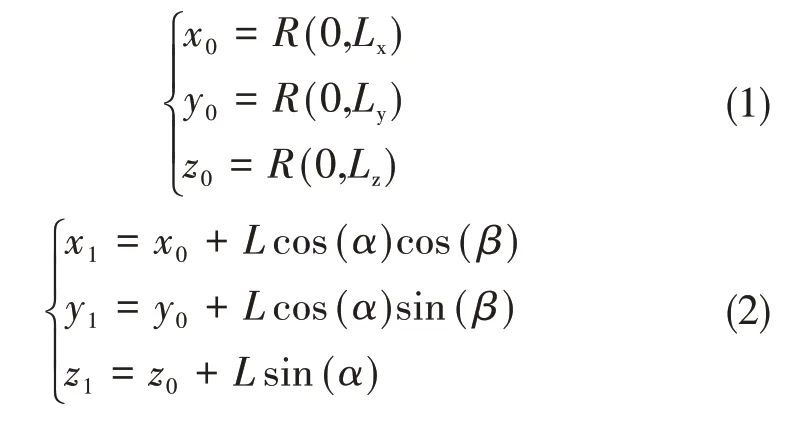
式中，R（0，Lx），R（0，Ly）和R（0，Lz）分别是范围为0 到Lx，Ly和Lz的随机函数，L为纤维长度。已有研究表明［6-7，15，24］：β～R（0，2π），随机分布函数R（0，2π）的范围为［0，2π］。对于角度β服从随机函数分布无需讨论，而角度α的分布规律基本上来源于材料烧结后截面内纤维分布的统计规律，因此在进行三维随机纤维材料微结构设计时，可以通过改变角度α的分布规律，确定三维随机纤维材料微结构。此外，已有的研究成果［15-17，25］表明：三维随机纤维材料IP方向的力学性能明显的高于TTT 方向，可以通过控制偏移纤维的数量调整三维随机纤维材料TTT 和IP 方向的力学性能。因此，假定角度α同样服从随机分布函数R（0，θ），其中，θ为纤维偏移的角度，另外设定参数PROB为纤维总数中与水平方向有夹角的纤维所占的比重。建立代表性体积单元过程中，首先，设置代表性体积单元参数：孔隙率P、纤维直径D、纤维长度L、纤维偏移角度θ、偏移纤维比重PROB等参数，在代表性体积单元中预生成总的纤维数目N[6]：

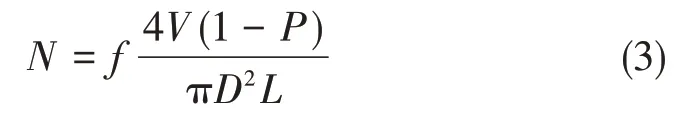
式中，V为代表性体积单元RVE 的体积（Lx×Ly×Lz），f为比例系数，在建模过程中可以通过控制比例系数f来调整预生成纤维的数目。

2.2 边界条件

图3给出了利用ANSYS 软件生成纤维的平面示意图，从图中可以看出：并非所有纤维都位于代表性体积单元中。

图3 代表性体积单元周期性边界条件生成示意图Fig.3 Diagram of periodic boundary condition in RVE

为了保证模型边界位移和应力连续，创建周期性边界。沿代表性体积单元边界切割模型，按照图3（a）中所示箭头方向平移位于代表性体积单元以外的纤维，平移距离为此方向模型宽度。代表性体积单元共计6 个边界，即平移6 次后可将所有位于代表性体积单元以外的纤维平移到代表性体积单元中，图3（b）给出了平移后的纤维分布示意图。为保证边界变形的连续，需在代表性体积单元边界施加满足周期性边界条件［7］。在模拟过程中，通过加载方向边界的支反力和模型横截面积之比，获得各个方向平均压缩应力：

式中，Sj表示表面j的面积，表示表面j上所有节点在i方向的支反力之和。因此，材料在各个加载方向的弹性模量可以写成Ei：

在建模过程中，为了简化分析，假设纤维长度L和直径D不变［7］。当代表性体积单元中任意两根纤维距离为D～2D时［15-16］，连接两者之间的公垂线，并将此公垂线看作一根新的短纤维，模拟两根纤维间的粘结部分。将获取两根纤维间的最短连接纤维问题，转换成了求解空间异面直线间公垂线的数学问题［26］。

2.3 纤维连接

在建模过程中，为了保证利用公垂线，连接所有设定距离范围内的纤维，并排除没有连接到一起的纤维，最终形成一个完整的网状结构。基于已有的选择算法［15-16］，选出所有纤维连接到一起后形成的最长纤维集合Lmax。如何选择第k根纤维所在的局部纤维集合，图4给出了一个简单描述：首先，选择第k根纤维，然后选择与这根纤维相交的纤维，紧接着选择与新的纤维集合中任意一根纤维相交的纤维，直到没有新的相交纤维为止，最后统计纤维集合的长度LGk，即可找出最长纤维集合Lmax。

图4 选择第k根纤维所在的局部纤维集合流程图Fig.4 Selection flowchart of the local fiber group with the k’th fiber

获得最长纤维集合Lmax后，计算代表性体积单元的真实孔隙率Pture，并且判断此孔隙率与设定孔隙率P之间的差值是否小于等于0.1%［15］。如果条件符合，则模型满足要求。否则，基于真实孔隙率Pture和设定孔隙率P之间的差值与初始比例系数f之和，获得一个新的比例系数f'。然后程序进入下一个循环过程，并根据新的比例系数f'生成新的总纤维数目N，直到建立符合条件的有限元模型。具体建模流程如图5所示，初始时比例系数f为1.12［16］。

图5 代表性体积单元的建立和计算流程图［16］Fig.5 Flowchart of algorithm for RVE setup and calculation

3 算例分析

3.1 纤维偏移角度θ对材料宏观力学性能的影响

在三维随机纤维材料结构设计过程中，可以通过调控纤维分布角度来调控材料宏观力学性能。选取纤维长度L=0.6 mm，纤维直径D=0.01 mm，孔隙率为90%的模型参数，建立代表性体积单元模型大小为Lx×Ly×Lz=L×L×L。分析偏移纤维比重PROB为10%、30%、70%和90%时的情况，并且偏移角度θ分别为10°、20°、30°、40°、50°和60°。图6给出了纤维偏移比重PROB为30%时，纤维偏移角度θ分别为10°和60°时对应的有限元模型。

图6 PROB为30%时代表性体积单元中纤维分布Fig.6 Fiber distribution in RVE when PROB is 30%

从图中可以看出：TTT 方向的截面内，纤维明显的随机分布；而IP 方向的截面内，偏移角度θ为10°时，可以明显看出纤维呈层状分布，少量的纤维与水平方向存在夹角，而偏移角度θ为60°时，虽然可以看出纤维有一定的层状分布，但是更多的纤维与水平方向有较大的夹角。此外，代表性体积单元TTT 和IP方向上的加载位移分别沿着z和y方向。

图7给出了三维随机纤维材料在不同纤维偏移角度θ下TTT 和IP 方向压缩强度随偏移纤维比重PROB的变化规律。从图中可以看出，偏移角度θ一定时，随着偏移纤维比重越来越高，则TTT 方向压缩强度逐渐升高，而IP 方向压缩强度逐渐降低。当偏移纤维比重一定时，例如，偏移纤维比重为90%时，TTT 方向压缩强度随着偏移角度θ的升高而明显增加，而IP方向的压缩强度变化却不明显。偏移角度θ越大，TTT方向压缩强度随着偏移纤维比重增加变化越剧烈，例如偏移角度θ为60°时，偏移纤维比重从30%增加到70%，TTT 方向压缩强度增加显著，而IP方向的压缩强度却明显降低。分析原因，可以归结为TTT 方向承载的纤维数量增加，而IP 方向承载纤维数量降低。已有研究表明［21］：孔隙率为89%的三维随机纤维材料TTT 方向的压缩强度约为（1.05±0.05）MPa（室温），IP 方向的压缩强度约为（4.05±0.6）MPa（573 K），低于有限元模型预测的三维随机纤维材料宏观力学能（PROB≥70%，θ≥40°）。因此，在材料制备过程中，可以通过控制纤维排布的装置及方法［27］调控纤维分布规律，获得TTT 与IP 方向压缩强度满足需求的三维随机纤维材料。

图7 不同纤维偏移角度θ下TTT和IP方向压缩强度σ随偏移纤维比重PROB的变化规律Fig.7 The compressive strength σ of TTT and IP directions with different sloped angle θ and sloped fiber rate PROB

3.2 纤维长短L对材料宏观力学性能的影响

选取纤维直径D=0.01 mm，偏移纤维比重PROB为10%，偏移角度θ为10°，孔隙率为90%，建立一个代表性体积单元模型的大小为Lx×Ly×Lz=L×L×L。图8给出了三维随机纤维材料压缩强度随纤维长度变化规律。从图中可以看出：TTT 和IP 方向三维随机纤维材料都随纤维长度增加呈上升的趋势，并且IP 方向压缩强度随长度增加而上升更明显。当纤维长度均值L=0.9 mm 左右时，两个方向压缩强度都呈下降的趋势。因此，在进行三维随机纤维材料制备的过程中，可以将石英纤维和莫来石纤维切成长度约为0.9 mm的短切纤维。

图8 压缩强度σ随纤维长度L的变化规律Fig.8 Variation trend between compressive strength σ and fiber length L

3.3 纤维直径D对材料宏观力学性能的影响

选取纤维长度L=0.6 mm，偏移纤维比重PROB为10%，偏移角度θ为10°，孔隙率为90%，建立一个代表性体积单元模型的大小为Lx×Ly×Lz=L×L×L。图9给出了三维随机纤维材料压缩强度随纤维直径变化规律。从图中可以看出：TTT方向压缩强度在纤维直径为6～8 μm 时呈上升的趋势，纤维直径为8～18 μm时，压缩强度持续降低；而IP方向压缩强度在纤维直径为6～8 μm 时无变化，纤维直径为8～10 μm 时，压缩强度呈上升趋势，10 μm以后压缩强度降低持续地降低，同时IP方向压缩强度随直径增加下降更明显。因此，在进行三维随机纤维材料制备的过程中，可以选取直径约为10 μm的石英纤维和莫来石纤维。