发射自适应置零数字多波束形成算法研究
2021-07-27高星,杨坡,徐磊
高 星,杨 坡,徐 磊
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
为了扩大相控阵雷达的同时观测空域范围以及搜索与跟踪数据率,相控阵天线必须具有发射多波束形成能力。传统相控阵雷达的发射多波束主要采用模拟方式产生,通过功分网络将信号分到各个通道中,再经过移相器对信号进行移相,实现扫描波束赋形。其主要缺点是一旦多波束网络确定之后,波束形状、相邻波束间隔以及它们的相交电平等便固定不变,难以对波束进行灵活控制,给调整和使用带来极大的困难。数字多波束则通过直接数字式频率合成器来完成发射工作,在数字域将信号进行加权处理后直接发射,具有灵活控制波束指向且方便实现发射波束的零点控制、超高分辨率或超低旁瓣等特点,为相控阵雷达实现多功能、同时多任务提供了技术基础,也为相控阵雷达实现灵活抗干扰提供了手段。本文在发射多波束形成的基础上,研究了自适应置零发射多波束的形成算法,其使得相控阵雷达发射波束在目标方向上形成窄的主波束,以增强目标信号;同时在干扰方向上形成零陷,以降低干扰对目标提取的影响。
1 发射数字多波束形成原理
发射数字波束形成与接收数字波束形成的原理相类似,下面以一维阵列为例来阐述发射数字多波束形成的原理。
如图1所示,由M
个全向阵元均匀排列组成阵列,阵元间间距为d
,发射信号为:
图1 发射多波束形成原理框图
s
(t
)=z
(t
)ej(1)
式中:w
为发射信号的载波角频率;z
(t
)为发射信号的复包络。设远场测试点S
与线阵的夹角为θ
(i
=1,2,3,…,M
),发射波在θ
方向上的等相位面为P
,则阵元m
(m
=1,2,3,…,k
)到达平面P
的传播延时可以表示为: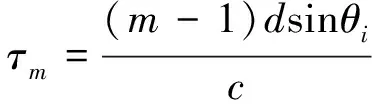
(2)
若阵元1的发射信号为s
(t
),则阵元m
的发射信号可以表示为:s
(t
+τ
)=z
(t
+τ
)ej(+)(3)
当发射信号为窄带信号时,其复包络是慢变化的,则阵元m
的发射信号可表示为:s
(t
+τ
)=s
(t
)ej=s
(t
)ej(4)
其中:
φ
=2πd
sinθ
/λ
(5)
将整个发射阵列写成向量形式:
(t
)=(θ
)s
(t
)(6)
(θ
)=[1 ej… ej(-1)](7)
式中:(θ
)为信号s
(t
)的方向矢量,其主要与发射角度θ
以及阵列几何结构有关。设发射阵列空域滤波器的权值为:
=[w
1w
1…w
](8)
对于方向为θ
的远场接收区,其能量分布为:
(9)
式中:φ
=2πd
sinθ
/λ
。写成向量形式:
(θ
)=s
(t
)(θ
)(10)
根据叠加原理,对同时k
个发射波束,输出的信号可以表示为:
(11)
2 发射自适应置零数字多波束形成算法
2.1 正交投影算法
正交投影自适应波束形成方法将期望导向矢量向干扰子空间的正交补空间投影,得到自适应权向量,从而使期望方向的波束与干扰方向正交。

(12)
从而可以得到自适应权向量:
=·(θ
)=(-)·(θ
)(13)

θ
),(θ
),…,(θ
))(14)
则在这一组基下的正交投影矩阵可以表示为:
=()(15)
进而自适应权向量可以表示为:=(-())·(θ
)(16)
2.2 线性约束最小方差算法
线性约束最小方差(LCMV)准则可以表示为:

(17)
式中:为协方差矩阵;为约束值矢量;为要求的最优权值;为约束矩阵,则其最优解可表示为:
(18)
发射自适应置零多波束形成可描述为如下的优化问题:
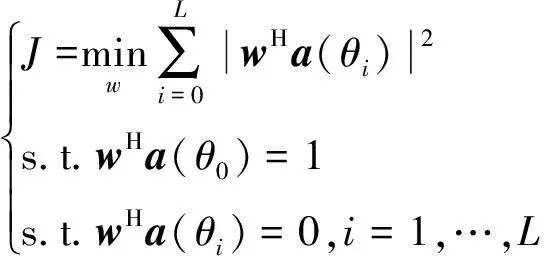
(19)
式中:θ
为期望方向;θ
为第i
个干扰方向,由于|(θ
)|=(θ
)(θ
),因此令:
(20)
式中:σ
是为了防止为奇异矩阵而做的对角加载。2.3导数约束加宽零陷算法
为了在角度θ
,θ
,…,θ
形成加宽零陷,只需要波束图P
(θ
)对θ
的高阶导数在θ
(i
=1,…,L
)处为0即可: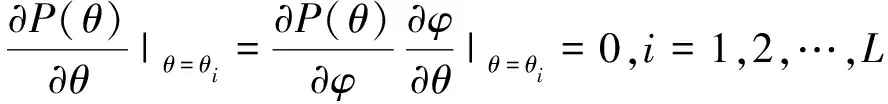
(21)
式中:φ
=πsin(θ
)。将方向图P
(θ
)=(θ
)代入上式求导得: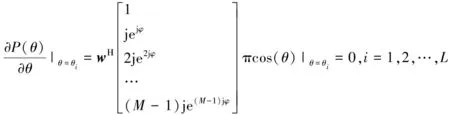
(22)
因此导数约束的宽零陷发射波束形成算法的改进优化问题等价于:
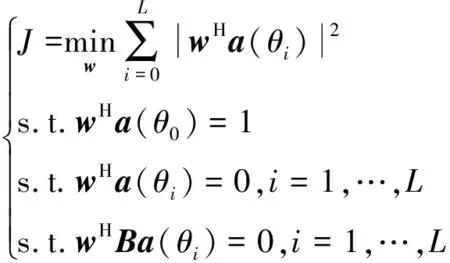
(23)
式中:=diag(0,1,…,M
-1)。令=[(θ
),(θ
),…,(θ
-1),(θ
),(θ
),…,(θ
-1)],对矩阵做奇异值分解可得:=(24)
式中:为的所有奇异值组成的对角矩阵。将M
阶酉矩阵表示为[]的形式,则根据奇异值分解的性质,可得上述优化问题的解为: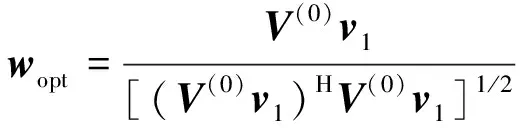
(25)
式中:为矩阵(θ
)(θ
)特征值分解后非零特征值所对应的特征向量。3 仿真分析
下面利用均匀线阵对发射自适应置零数字多波束形成算法进行仿真分析。
3.1 正交投影算法
阵元间距为发射信号的半波长,阵元个数为32,3 dB波束宽度为3.1°,同时发射5个波束,波束指向分别为(-10°,-3.1°,0°,3.1°,30°),采用正交投影算法仿真结果如图2所示。

图2 正交投影算法自适应置零仿真图(最小间隔3.1°)
阵元间距为发射信号的半波长,阵元个数为32,4 dB,波束宽度为3.6°,同时发射5个波束,波束指向分别为(-10°,-3.6°,0°,3.6°,30°),采用正交投影算法,仿真结果如图3所示。

图3 正交投影算法自适应置零仿真图(最小间隔3.6°)
由仿真图2、图3可知,5个发射波束均在除自身以外的其它4个波束主瓣方向上形成了零陷,实现了发射多波束之间的隔离。由图2可知,发射波束最小间隔为3 dB、波束宽度为3.1°的2个波束主瓣都偏离了期望方向,而且第一副瓣电平也有所提高。由图3可知,发射波束最小间隔为4 dB、波束宽度为3.6°时,波束主瓣方向未发生偏移,波束第一副瓣也未发生变化。因此,在实际工程应用中,正交投影算法自适应置零多波束形波束指向间隔不能小于4 dB波束宽度。
3.2 线性约束最小方差算法
阵元间距为发射信号的半波长,阵元个数为32,3 dB波束宽度为3.1°,同时发射5个波束,波束指向分别为(-10°,-3.1°,0°,3.1°,30°),采用线性约束最小方差算法,仿真结果如图4所示。

图4 线性约束最小方差算法自适应置零仿真图(最小间隔3.1°)
阵元间距为发射信号的半波长,阵元个数为32,4 dB波束宽度为3.6°,同时发射5个波束,波束指向分别为(-10°,-3.6°,0°,3.6°,30°),采用线性约束最小方差算法,仿真结果如图5所示。

图5 线性约束最小方差算法自适应置零仿真图(最小间隔3.6°)
由仿真图4、图5可知,与正交投影算法类似,5个发射波束在除自身以外的其它4个波束主瓣方向上形成了零陷,在最小波束间隔为3.1°的2个波束主瓣都偏离了期望方向,第一副瓣电平也有所提高,而在波束宽度为3.6°时,波束主瓣方向未发生偏移,波束第一副瓣也未发生变化。因此,同正交投影算法,线性约束最小方差算法要求波束指向间隔不能小于4 dB波束宽度。
3.3 导数约束加宽零陷算法
阵元间距为发射信号的半波长,阵元个数为32,4 dB波束宽度为3.6°,同时发射5个波束,波束指向分别为(-30°,-3.6°,0°,3.6°,30°),采用导数约束加宽零陷算法,仿真结果如图6所示。

图6 导数约束加宽零陷算法自适应置零仿真图(最小间隔3.6°)
阵元间距为发射信号的半波长,阵元个数为32,3 dB波束宽度为3.1°,同时发射5个波束,波束指向分别为(-30°,-5.6°,0°,5.6°,30°),采用导数约束加宽零陷算法,仿真结果如图7所示。

图7 导数约束加宽零陷算法自适应置零仿真图(最小间隔4°)
由仿真图6、图7可知,使用导数约束加宽零陷算法,5个发射波束在除自身以外的其它4个主瓣方向形成了零陷,并且有效地加宽了零陷,然而其主瓣有所展宽。由图6可知,4 dB波束宽度间隔时的主瓣都偏离了期望方向,因此4 dB波束宽度间隔已不能满足波束隔离要求。通过仿真计算,当采用5.6°(3 dB波束宽度的1.8倍)时,主瓣都回归了期望方向,因此导数约束加宽零陷算法下的主瓣间隔不能小于3 dB波束宽度的1.8倍。
4 结束语
本文介绍了几种发射自适应置零多波束形成算法,包括正交投影算法、线性约束最小方差算法以及导数约束加宽零陷算法,对每种方法都进行了仿真分析。通过仿真分析可以看出,每种波束形成算法都有其优点与不足,正交投影算法、线性约束最小方差算法要求的波束间隔窄,但零陷宽度不够宽,导数约束加宽零陷算法虽然零陷宽度宽,但相应地要求波束间隔变大。实际工程应用中,由于干扰角度估计存在一定的误差,另外当干扰处于高速运动时,会造成自适应权失配,干扰跳出零陷区域,因此实际应用时建议使用导数约束加宽零陷算法,扩大零陷宽度,增加系统的鲁棒性。当然,对于干扰方向固定的干扰则可以采用正交投影算法和线性约束最小方差算法,以降低对波束间隔的要求。
