基于SSC盲移频的NLFM雷达干扰技术研究
2021-07-27周文彬赵忠凯郭晓冉
周文彬,赵忠凯,郭晓冉
(1.哈尔滨工程大学,黑龙江 哈尔滨 150001;2.解放军 32181 部队,河北 石家庄 050000)
0 引 言
脉冲压缩体制雷达是现代电子战中应用最广泛的雷达之一,其采用的调频信号具有大的时宽与带宽积,较好地解决了探测距离和距离分辨率之间的问题。其中最常用的脉冲压缩信号有线性调频(LFM)信号和非线性调频信号(NLFM)。其中LFM信号经过脉冲压缩后的副瓣较高,为了抑制副瓣通常会进行加窗处理,然而窗函数加权会引起信号的信噪比损失和主瓣展宽的问题。NLFM信号进行脉冲压缩后具有副瓣低的优点,不需要做窗函数加权处理,避免了信噪比损失,并且NLFM频率变化的速率不恒定。与LFM信号相比,NLFM信号具有更好的检测率特性和更准确的测量范围,以及更好的侦察效果,因此对非线性调频信号进行干扰具有非常重要的意义。由于脉冲压缩体制的雷达信号在时间和频率上具有强耦合性,频率上的偏移会造成时间上的改变。在截获的雷达信号的频域上增加1个移频量,会导致时域上产生一段欺骗距离,从而生成具有欺骗效果的欺骗假目标干扰。然而传统的移频干扰存在着难以克服的缺点,即需要事先测得雷达的先验信息。在遇到调频斜率捷变雷达时,由于难以实时获取雷达的调频斜率,移频量不能随调频斜率的改变而改变,产生假目标的位置会发生跳变,容易被雷达识别出来,从而失去干扰效果。
王玉军在《对LFM雷达的N
阶SSC盲移频干扰算法》中提出了一种N
阶频谱扩展-压缩(SSC)的方法,即对截获的雷达信号做N
阶和N
-1阶频谱扩展后,用后者的延时共轭对前者做脉冲压缩。生成的盲移频干扰信号只与阶数N
和延时τ
有关,可以很好地应对捷变频雷达。为了应对调频斜率捷变的S型NLFM信号,本文提出了一种基于SSC盲移频的NLFM信号干扰技术,并通过理论分析和仿真验证,证明了其可行性。1 NLFM信号模型
传统的LFM信号的自相关旁瓣较高,通常需要在雷达接收端进行加窗处理来抑制旁瓣,从而导致了信噪比的损失。为了减小信噪比的损失,提出了NLFM信号。NLFM信号是指频率调制函数为非线性函数的一类信号,由于其通过匹配滤波器后副瓣低,减小了信噪比损失而被广泛应用在脉冲压缩体制雷达中。目前比较常见的NLFM信号有S型调制信号。
S型NLFM信号的频率变化曲线呈S型变化,其频率调制信号的表达式为:
s
(t
)=A
rect(t/T
)exp{j[2πf
t
+φ
(t
)]}(1)
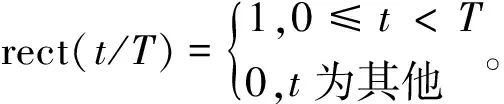
本文选取的窗函数为Hamming窗,Hamming窗函数的表达式为:

(2)
式中:B
为信号带宽。利用相位的驻留原理,可以近似得到信号的群延时函数t
(f
):
(3)
式中:m
为调频因子,其取值范围为[0,1]。对式(3)求反函数即可得到NLFM信号的调频函数f
(t
):f
(t
)=t
(f
)(4)
对调频函数积分,得到NLFM信号的相位函数φ
(t
):
(5)
可以得到S型NLFM信号的表达式:
s
(t
)=A
exp{jφ
(t
)}(6)
2 SSC盲移频干扰算法原理
移频干扰是对抗脉冲压缩雷达的一种有效手段。其利用数字射频储频器(DRFM)技术截取并存储雷达信号,通过对截取到的雷达信号进行处理,并附加1个移频量,利用脉冲压缩体制雷达信号时间和相位之间具有耦合性的特点,频率上的改变会导致时间域的改变,从而产生了移频假目标。移频量越大,假目标距离回波信号越远,匹配滤波增益越小;移频量越小,假目标距离回波信号越近,匹配滤波增益越大。
但是当雷达的调频斜率不断变化时,由于干扰方不能实时测得调频斜率的变化,干扰距离会发生变化,从而被雷达识别出来失去干扰效果。因此传统的移频干扰难以应对调频斜率变化的S型NLFM信号。
为了应对S型NLFM信号,可以采用SSC盲移频干扰。SSC盲移频干扰的原理是:通过对采样到的雷达信号及其延时信号做N
阶和N
-1阶频谱扩展,并利用后者对前者进行脉冲压缩,能够产生固定位置的假目标。由于其不需要测得雷达信号的参数,因此能够很好地应对调频斜率捷变的雷达。具体的干扰处理框图如图1所示。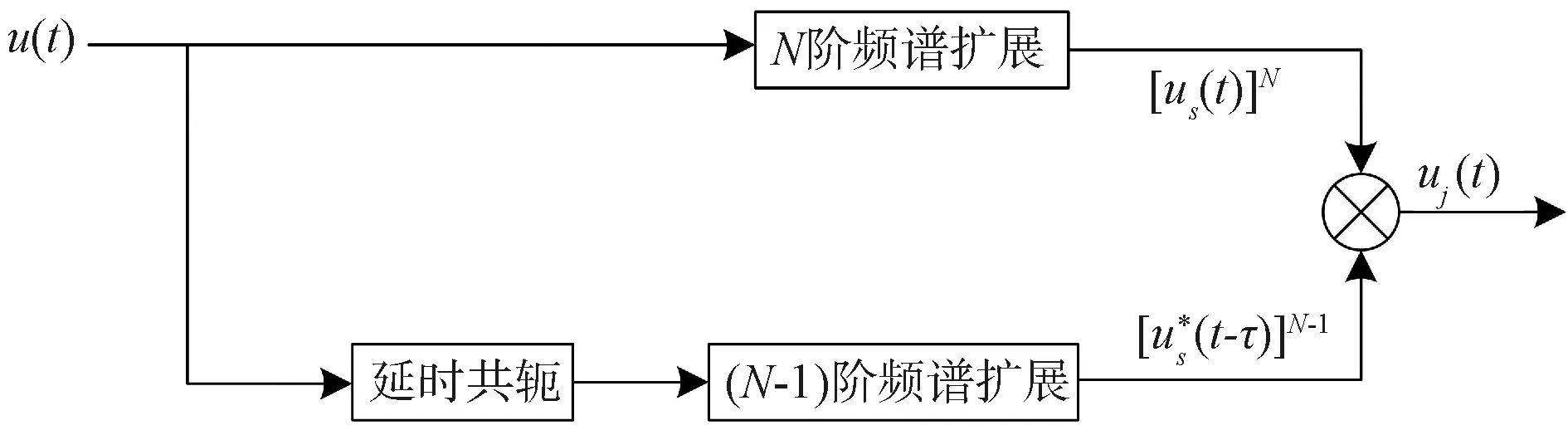
图1 SSC盲移频信号生成流程图
本文以S型NLFM信号为例进行分析。假设截获的雷达信号形式如式(1),对其做SSC盲移频干扰处理。
对S型NLFM信号做N
阶频谱扩展得到:[s
(t
)]=A
exp{jNφ
(t
)}(7)
对S型NLFM信号的延时共轭做N
-1阶频谱扩展得: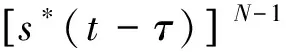
(8)
将式(7)和式(8)相乘即可得到S型NLFM信号的N
阶SSC盲移频干扰信号:s
(t
)=[s
(t
)][s
(t
-τ
)]-1=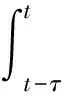
(9)
由式(9)可以得出,假目标与回波信号的距离为:

(10)
由式(10)可以得出,干扰假目标的欺骗距离仅与系统参数N
和干扰机处理延时τ
有关。即使雷达信号的中心频率、带宽或者脉宽发生了改变,假目标和真实目标之间的距离也不会改变。3 仿真结果分析
假设NLFM信号的脉宽T
=100 μs,带宽B
=20 MHz,采样频率f
=100 MHz,调频因子m
=0.07,加入信噪比为20 dB的高斯白噪声,选取Hamming窗函数。通过计算可以得到该S型NLFM信号的时频曲线,将生成的S型NLFM信号通过匹配滤波器,得到其脉冲压缩图。仿真结果如图2所示。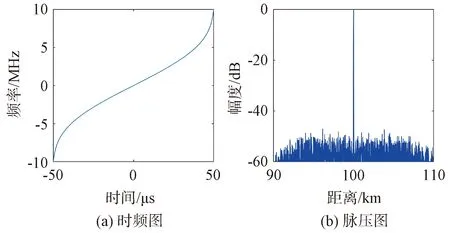
图2 信号时频图与脉压图
观察图2(a)可以发现,S型NLFM信号的时频曲线呈S形变化,曲线的弯曲程度跟调频因子m
有关,m
越小弯曲程度越大,m
越大弯曲程度越小。当m
=1时,信号的时频曲线变成一条直线,NLFM信号变成LFM信号。因此,可以把LFM信号看作NLFM信号的一种特殊情况。观察图2(b),S型NLFM信号经过脉冲压缩后信号主瓣宽度很窄,副瓣与LFM信号相比有所降低。且副瓣的降低幅度与调频因子m
有关,调频因子m
越小,副瓣越低,主瓣有一定程度的展宽;调频因子m
越大,副瓣越高,主瓣越窄。假设截取S型NLFM信号的带宽、脉宽和调频因子保持不变。为了得到干扰距离为1.2 km的干扰假目标,由式(10)可以取SSC盲移频干扰的系统阶数N
为3,干扰机处理延时τ
为4 μs。将SSC盲移频信号通过匹配滤波器后,仿真得到NLFM信号和SSC盲移频干扰信号的脉冲压缩图如图3所示。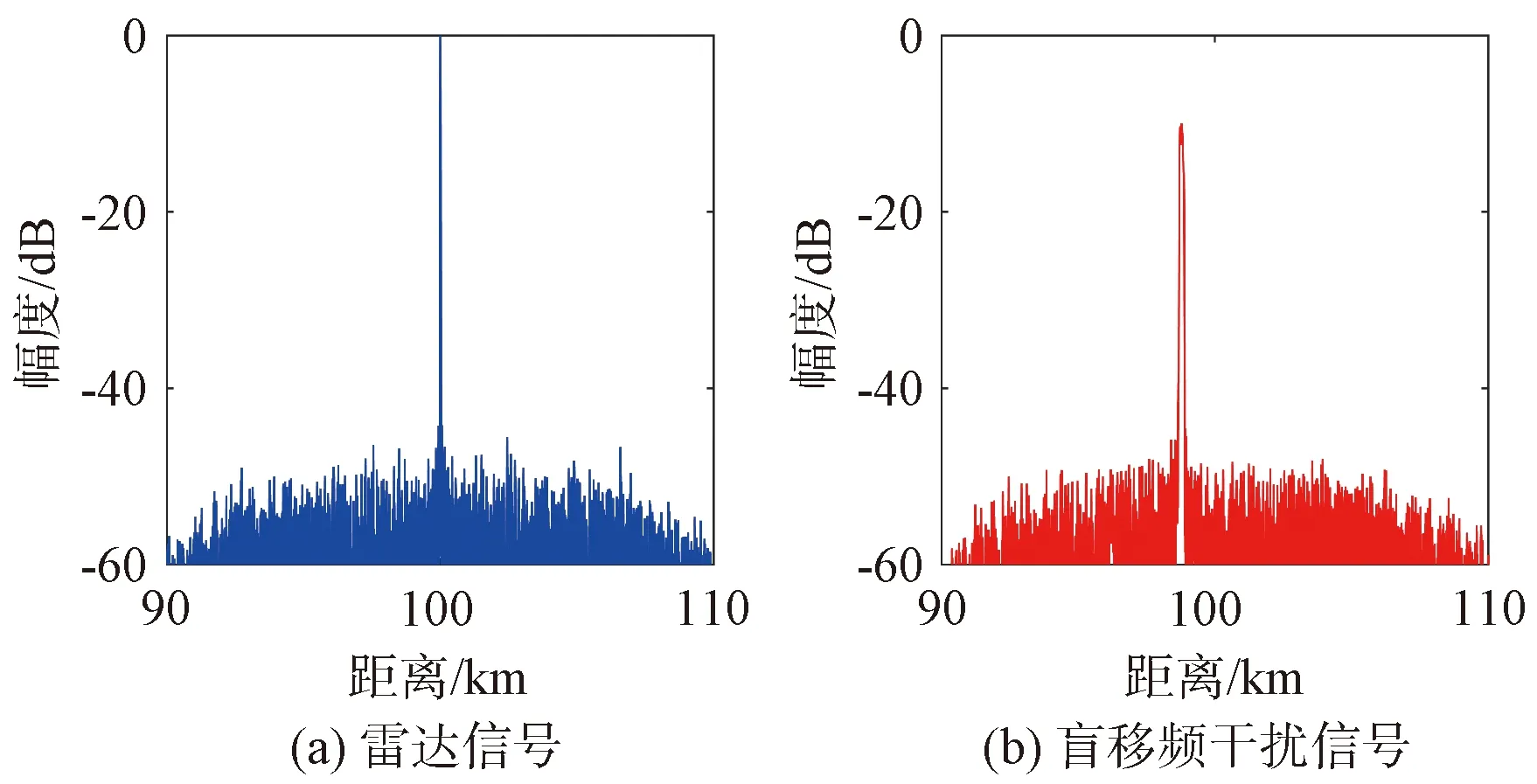
图3 信号脉压图
观察图3可以发现,SSC盲移频干扰假目标与NLFM目标信号距离1.2 km,对S型NLFM信号具有干扰效果。
分别取NLFM信号的脉宽为100 μs和50 μs,保持其他参数不变,仿真得到NLFM信号和SSC盲移频干扰信号的脉冲压缩图如图4所示。

图4 雷达信号与干扰信号脉压图
观察图4可以发现,当NLFM信号的参数改变时,保持SSC盲移频干扰的系统阶数和干扰机处理延时不变,干扰信号的位置保持不变。说明SSC盲移频干扰能够很好地隐藏信号特征参数,有效地对抗调频斜率捷变的雷达。
保持雷达信号的参数不变,取SSC盲移频干扰信号的系统阶数为3,干扰机处理延时分别为2 μs、4 μs,得到NLFM信号和盲移频干扰信号的脉冲压缩图如图5所示。
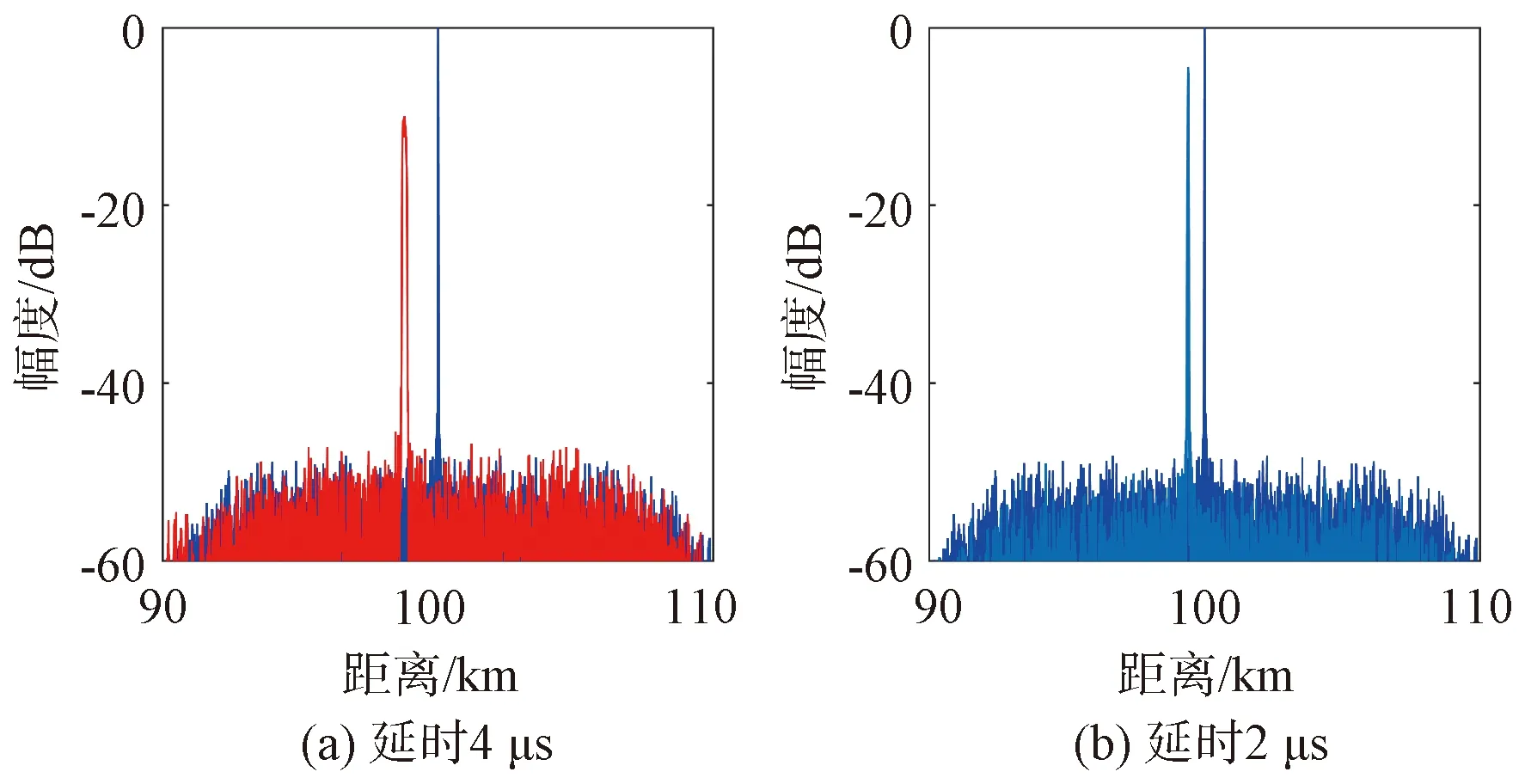
图5 不同延时SSC信号脉压图
图5(a)是干扰机处理延时为4 μs时的脉压图,图5(b)是干扰机处理延时为2 μs时的脉压图。在系统阶数不变的情况下,干扰机处理延时越大,SSC盲移频干扰信号距离目标信号越远,匹配滤波增益越小,主瓣宽度越宽。
4 结束语
本文提出了一种基于SSC盲移频的NLFM雷达干扰算法,可以产生特定位置的假目标干扰信号,且假目标信号的位置不随雷达信号的改变而改变。分析推导了系统阶数和干扰机延时对干扰假目标的影响。最后通过仿真验证了该算法的可行性,具有一定的工程应用价值。
